Zero foundation introduction depth learning lesson 1
The relationship between artificial intelligence, machine learning and deep learning

artificial intelligence
As the literal meaning, artificial intelligence is a new technical science to develop theories, methods, technologies and application systems for simulating, extending and expanding human intelligence. Because this definition only expounds the goal and does not limit the method, many methods and branches to realize artificial intelligence have turned it into a "hodgepodge" discipline.
machine learning
Machine learning is a special study of how computers simulate or realize human learning behavior, so as to obtain new knowledge or skills, reorganize the existing knowledge structure and continuously improve its own performance. Its implementation method can be divided into two steps: training and prediction, which is similar to our familiar induction and deduction.

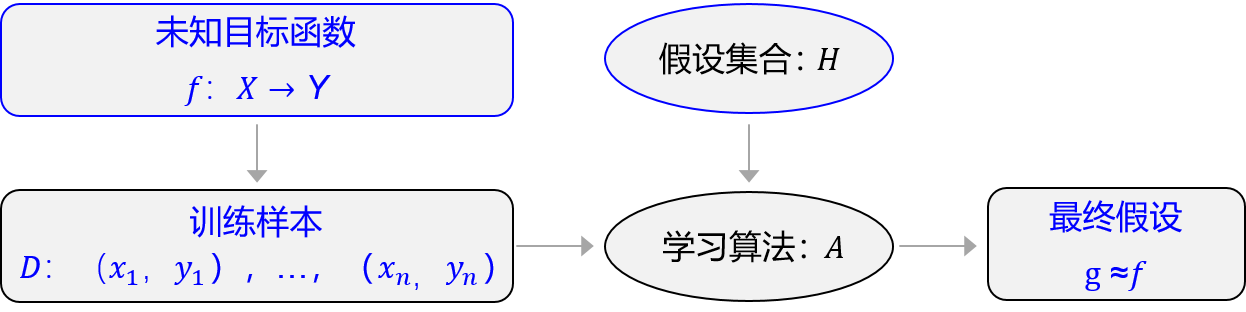
The process of machine learning is basically the same as that of Newton's second law, which is divided into three stages: hypothesis, evaluation and Optimization:
Hypothesis: by observing the observed data of acceleration a and force F, it is assumed that a and F are linear, that is, a=w ⋅ F.
Evaluation: the fitting effect on the known observation data is good, that is, the result of w ⋅ F calculation should be as close as possible to the observed a.
Optimization: among all possible values of parameter W, it is found that w=1/m can make the evaluation the best (the best fitting observation sample).
The essence of machine learning is to find parameters and fit a large formula
Deep learning
Compared with traditional machine learning algorithms, the two are consistent in theoretical structure, that is, model assumptions, evaluation functions and optimization algorithms. The fundamental difference lies in the complexity of assumptions, as follows:
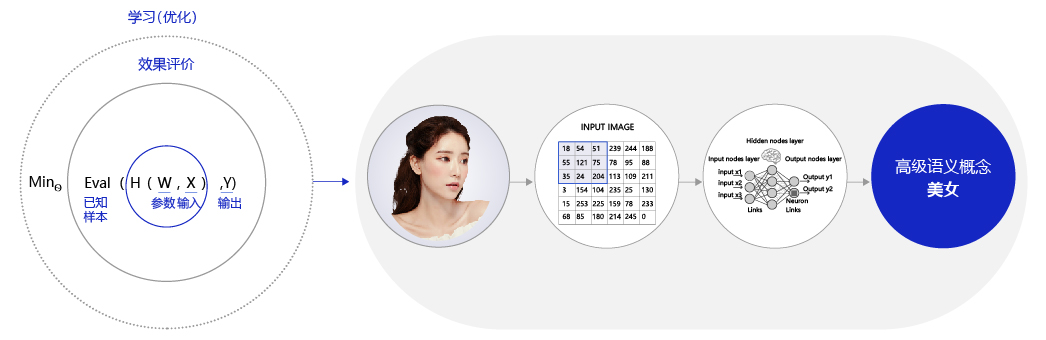
After inputting the beauty picture, the computer can only receive a digital matrix. For the advanced semantic concept of beauty, the complexity of information transformation from pixel to advanced semantic concept is unimaginable! This transformation can no longer be expressed by mathematical formula, so researchers use the structure of human brain neurons for reference to design the model of neural network.
Basic concepts of neural network
Artificial neural network includes multiple neural network layers, such as convolution layer, full connection layer, LSTM, etc. each layer includes many neurons. Nonlinear neural networks with more than three layers can be called deep neural networks. Generally speaking, the deep learning model can be regarded as the mapping function from input to output, such as the mapping from image to advanced semantics (beauty). A deep enough neural network can fit any complex function in theory.
Therefore, neural network is very suitable for learning the internal law and representation level of sample data, and has good applicability to text, image and voice tasks.
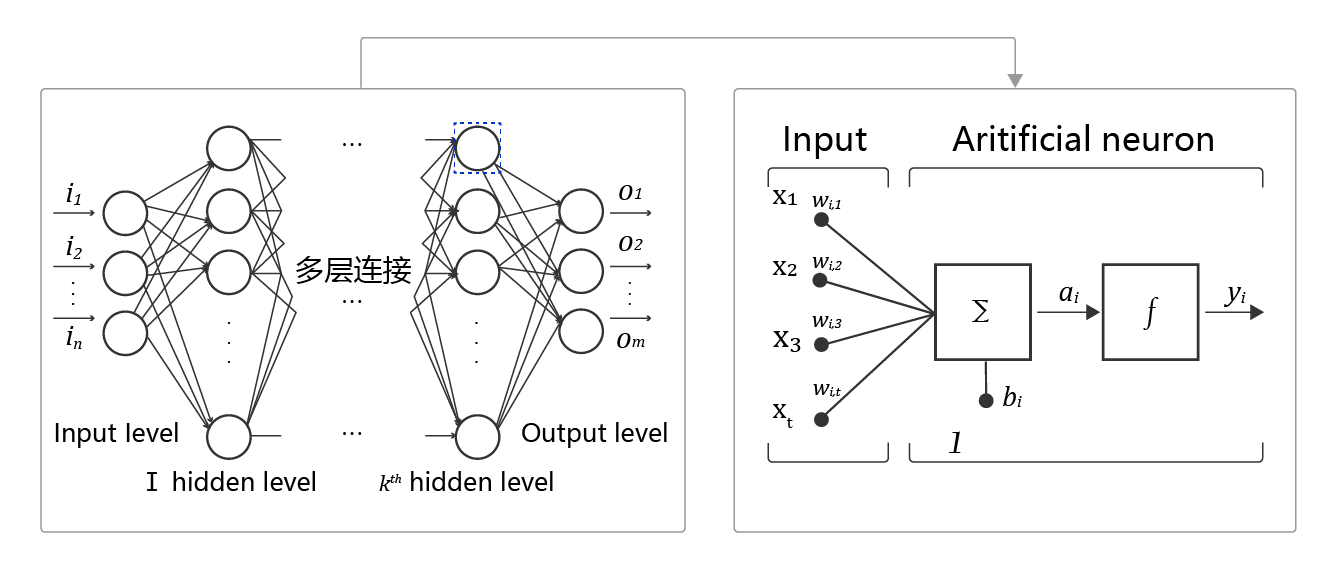
Neuron: each node in the neural network is called neuron and consists of two parts:
Weighted sum: weighted sum of all inputs.
Nonlinear transformation (activation function): the result of weighted sum is transformed by a nonlinear function, which makes the neuron calculation have nonlinear ability.
Multilayer connection: a large number of such nodes are arranged according to different levels to form a multilayer structure, which is called neural network.
Forward calculation: the process of calculating the output from the input, in order from the front of the network to the back.
Calculation diagram: it shows the calculation logic of neural network in a graphical way, which is also called calculation diagram. We can also express the calculation diagram of neural network in the form of formula, as follows:
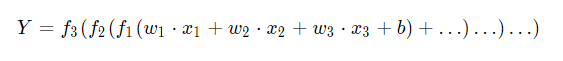

Case: Boston house price
Boston house price forecasting is a classic machine learning task, and its importance is equivalent to the "hello world" in the program.
House prices in Boston are affected by many factors, including 13 factors that may affect house prices and the average price of this type of house, as follows:

The prediction problem can be divided into regression task and classification task according to whether the type of prediction output is continuous real value or discrete label. Because house price is a continuous value, house price prediction is obviously a regression task.
Linear regression prediction model
Linear regression model is the simplest regression model. It is assumed that the influence relationship between house price and various factors can be expressed by the following formula:
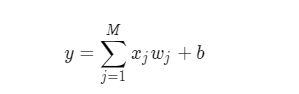
The solution of the model is to fit the weight slope Wj and offset term b through the data
In this case, we generally use the mean square error as the loss function (rationality and easiness):
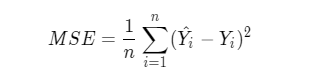
In the standard structure of neural network, each neuron is composed of weighted sum and nonlinear transformation, and then multiple neurons are placed and connected to form a neural network.
The linear regression model can be regarded as a minimalist special case of the neural network model, which is a neuron with only weighted sum and no nonlinear transformation (and no network is required), as follows:

model building
Generally, there are five steps to build the model
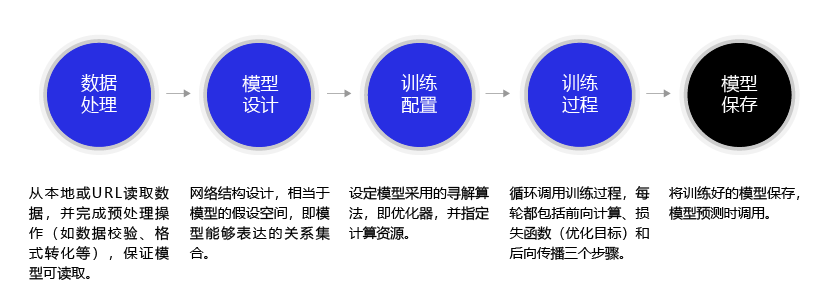
data processing
Data processing includes five parts: data import, data shape transformation, data set division, data normalization and encapsulation of load data function. Only after data preprocessing can it be called by the model.
#Import the required package s import numpy as np import json # Read in training data datafile = './work/housing.data' data = np.fromfile(datafile, sep=' ') data

The imported data is one-dimensional, so we transform it into 14 columns of data (13 X influencing factors and one Y output)
# Here, reshape the original data into the form of N x 14
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])
# View data
x = data[0]
print(x.shape)
print(x)

The data set is divided into training set and test set. The training set is used to determine the parameters of the model, and the test set is used to evaluate the effect of the model.
ratio = 0.8 offset = int(data.shape[0] * ratio) training_data = data[:offset] training_data.shape
Data set normalization
# Calculate the maximum, minimum and average values of the train dataset
maximums, minimums, avgs = \
training_data.max(axis=0), \
training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# Normalize the data
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
Encapsulated as load data function
Encapsulate the above data processing operations into the load data function for the next model call. The implementation method is as follows.
def load_data():
# Import data from file
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# Each data includes 14 items, of which the first 13 items are influencing factors and the 14th item is the corresponding median house price
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# Reshape the original data into a shape like [N, 14]
data = data.reshape([data.shape[0] // feature_num, feature_num])
# Split the original data set into training set and test set
# Here, 80% of the data are used for training and 20% for testing
# There must be no intersection between training and testing
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# Calculate the maximum, minimum and average of the training set
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# Normalize the data
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# Division ratio of training set and test set
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
Data processing has come to an end
Note: the normalization of test set is also the maximum and minimum standard of training set (limited to a certain range)
verification:
# get data training_data, test_data = load_data() x = training_data[:, :-1] y = training_data[:, -1:]
model design
Model design is one of the key elements of deep learning model, also known as network structure design, which is equivalent to the hypothesis space of the model, that is, the process of realizing the "forward calculation" (from input to output) of the model.
If both the input feature and the output prediction value are represented by vectors, and the input feature x has 13 components and y has 1 component, the shape of the parameter weight is 13 × 1.
Initialization is as follows:
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0] w = np.array(w).reshape([13, 1])
For a complete linear regression formula, it is also necessary to initialize the offset bbb and assign the initial value of - 0.2 at will. Then, the complete output of the linear regression model is z=x*w+b. this process of calculating the output value from the characteristics and parameters is called "forward calculation"
The above process of calculating and predicting the output is described in the form of "class and object". The class member variables include parameters w and b. Write a forward function (representing "forward calculation") to complete the above calculation process from characteristics and parameters to output predicted value. The code is as follows.
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program,
# A fixed random number seed is set here
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
Based on the definition of Network class, the calculation process of the model is as follows.
net = Network(13) x1 = x[0] y1 = y[0] z = net.forward(x1) print(z)
Training configuration
After the model design is completed, it is necessary to find the optimal value of the model through training configuration, that is, to measure the quality of the model through the loss function. Training configuration is also one of the key elements of deep learning model.
The mean square error formula is as follows:
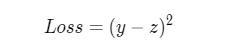
Mean square error is often used in regression problems and cross entropy loss function is often used in classification problems
When calculating the loss function, we need to take the loss function value of each sample into account, so we need to sum the loss function of a single sample and divide it by the total number of samples N
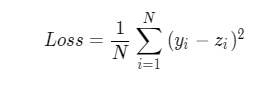
The code is defined as follows:
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program, a fixed random number seed is set here
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
The tests are as follows:
net = Network(13)
# Here, the predicted value and loss function of multiple samples can be calculated at one time
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
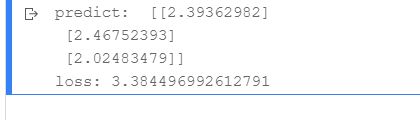
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)
Training process
The training process is one of the key elements of the deep learning model. Its goal is to make the defined Loss function Loss as small as possible, that is to find a parameter solution w and b to make the Loss function obtain a minimum.

As shown in the figure, the slope at the extreme point of the curve is 0, that is, the derivative of the function at the extreme point is 0. Then, w and b, which minimize the loss function, should be the solutions of the following equations:
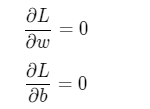
However, it is not easy to solve the model with nonlinear variance. In order to solve this problem, we will introduce a more general numerical solution method: gradient descent method.
Gradient descent method
In reality, there are a large number of functions, which are easy to solve in the forward direction, but difficult to solve in the reverse direction. They are called one-way functions, which have a large number of applications in cryptography. The characteristic of cipher lock is that it can quickly judge whether a key is correct (it is easy to find y when x is known), but even if the cipher lock system is obtained, it can not crack what the correct key is (it is difficult to find x when y is known).
This situation is particularly similar to a blind man who wants to walk from the peak to the valley. He can't see where the valley is (he can't reverse solve the parameter value when the Loss derivative is 0), but he can stretch out his feet to explore the slope around him (the derivative value of the current point, also known as the gradient). Then, the minimum value of Loss function can be solved in this way: from the current parameter value, step by step in the downhill direction until it reaches the lowest point. This method is called "blind downhill method" or "gradient descent method".
Example: consider the case where there are only two parameters W5 and W9
net = Network(13)
losses = []
#Only the curve part of parameters w5 and w9 in the interval [- 160, 160] and the extreme value including the loss function are drawn
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#Calculate the Loss corresponding to each parameter value in the setting area
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#Use matplotlib to plot the two variables and the corresponding Loss as a 3D graph
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()

Observe that the above curve shows a "smooth" slope, which is one of the reasons why we choose the mean square error as the loss function. Figure 6 shows the loss function curve of mean square error and absolute value error (only the error of each sample is accumulated without square processing) when there is only one parameter dimension.
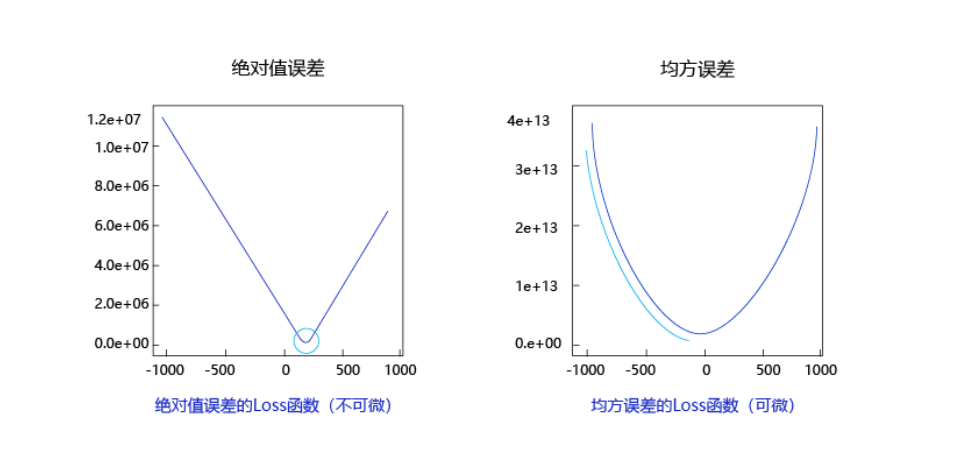
The advantages of using mean square error are as follows:
(1) The lowest point of the curve is differentiable.
(2) The closer to the lowest point, the slope of the curve will gradually slow down, which is helpful to judge the degree of approaching the lowest point through the current gradient (whether to gradually reduce the step size to avoid missing the lowest point)
The scheme to realize the gradient descent method is as follows:
(1) Randomly select a set of initial values
(2) Select a point to make the error smaller
(3) Repeat step 2 until the loss function hardly drops
The basic knowledge of calculus tells us that along the opposite direction of the gradient, the function value decreases the fastest: the gradient direction of the function at a certain point is the direction with the largest slope of the curve, but the gradient direction is upward, so the opposite direction of the gradient decreases the fastest.
Calculated gradient
The loss function is defined as follows:

When considering a sample:

View each data scale
x1 = x[0]
y1 = y[0]
z1 = net.forward(x1)
print('x1 {}, shape {}'.format(x1, x1.shape))
print('y1 {}, shape {}'.format(y1, y1.shape))
print('z1 {}, shape {}'.format(z1, z1.shape))

#Calculate the gradient of w0 according to the above formula
gradient_w0 = (z1 - y1) * x1[0]
print('gradient_w0 {}'.format(gradient_w0))
#Calculate the gradient of w1
gradient_w1 = (z1 - y1) * x1[1]
print('gradient_w1 {}'.format(gradient_w1))
#and so on
Gradient calculation using Numpy
Based on Numpy broadcast mechanism (the calculation of vector and matrix is the same as that of a single variable), gradient calculation can be realized more quickly,
The result is a 13 dimensional vector, and each component represents the gradient of that dimension.
gradient_w = (z1 - y1) * x1
print('gradient_w_by_sample1 {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))

Similarly, calculate the gradient of multiple samples
x3 = x[2]
y3 = y[2]
z3 = net.forward(x3)
gradient_w = (z3 - y3) * x3
print('gradient_w_by_sample3 {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))
# Note that this is the data of three samples at a time, not the third sample
x3samples = x[0:3]
y3samples = y[0:3]
z3samples = net.forward(x3samples)
print('x {}, shape {}'.format(x3samples, x3samples.shape))
print('y {}, shape {}'.format(y3samples, y3samples.shape))
print('z {}, shape {}'.format(z3samples, z3samples.shape))
For the case with N samples, we can directly calculate the contribution of all samples to the gradient in the following way, which is the convenience brought by using the broadcast function of Numpy library.
z = net.forward(x)
gradient_w = (z - y) * x
print('gradient_w shape {}'.format(gradient_w.shape))
print(gradient_w)
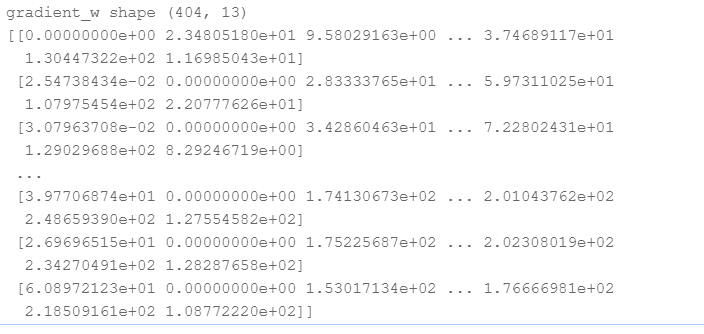
Gradient above_ Each row of W represents the contribution of a sample to the gradient. According to the gradient calculation formula, the total gradient is the average value of each sample's contribution to the gradient.
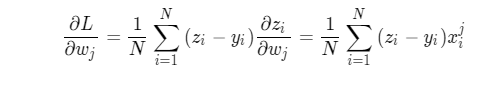
# axis = 0 means adding each row and then dividing by the total number of rows
gradient_w = np.mean(gradient_w, axis=0)
print('gradient_w ', gradient_w.shape)
print('w ', net.w.shape)
print(gradient_w)
print(net.w)

np. The 0-th dimension is eliminated in the mean function. Therefore, in order to ensure the consistency of dimensions, we use the following code:
gradient_w = gradient_w[:, np.newaxis]
print('gradient_w shape', gradient_w.shape)
Calculate gradient total code
z = net.forward(x) gradient_w = (z - y) * x gradient_w = np.mean(gradient_w, axis=0) gradient_w = gradient_w[:, np.newaxis] gradient_w gradient_b = (z - y) gradient_b = np.mean(gradient_b) # Here b is a numerical value, so you can directly use NP Mean gets a scalar gradient_b
Write the above process of calculating the gradient of w and b into the gradient function of Network class. The implementation method is as follows.
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program, a fixed random number seed is set here
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
verification:
# Call the gradient function defined above to calculate the gradient
# Initialize network
net = Network(13)
# Set [w5, w9] = [-100., -100.]
net.w[5] = -100.0
net.w[9] = -100.0
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))
Determine the point where the loss function is smaller
Next, we begin to study the method of updating the gradient. First, move a small step along the opposite direction of the gradient, find the next point P1 and observe the change of the loss function.
# On the [w5, w9] plane, move to the next point P1 along the opposite direction of the gradient
# Define moving step eta
eta = 0.1
# Update parameters w5 and w9
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
# Recalculate z and loss
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))
eta: controls the magnitude of each parameter value change along the opposite direction of the gradient, that is, the step size of each movement, also known as the learning rate.
You can think about why we should normalize the input features to keep the scale consistent before? This is to make the uniform step more appropriate.

Encapsulate train function
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program, a fixed random number seed is set here
np.random.seed(0)
self.w = np.random.randn(num_of_weights,1)
self.w[5] = -100.
self.w[9] = -100.
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w5, gradient_w9, eta=0.01):
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
def train(self, x, y, iterations=100, eta=0.01):
points = []
losses = []
for i in range(iterations):
points.append([net.w[5][0], net.w[9][0]])
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
self.update(gradient_w5, gradient_w9, eta)
losses.append(L)
if i % 50 == 0:
print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))
return points, losses
# get data
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# Create network
net = Network(13)
num_iterations=2000
# Start training
points, losses = net.train(x, y, iterations=num_iterations, eta=0.01)
# Draw the change trend of the loss function
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

Training extended to all parameters
The gradient descent process demonstrated by the plane only includes w5 and w9 parameters, but the complete model of house price prediction must solve all parameters w and b
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program, a fixed random number seed is set here
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=100, eta=0.01):
losses = []
for i in range(iterations):
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(L)
if (i+1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# get data
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# Create network
net = Network(13)
num_iterations=1000
# Start training
losses = net.train(x,y, iterations=num_iterations, eta=0.01)
# Draw the change trend of the loss function
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
Random gradient descent method
In the above program, each loss function and gradient calculation is based on the full amount of data in the data set. For the Boston house price forecasting task data set, the number of samples is relatively small, only 404. However, in practical problems, the data set is often very large. If the full amount of data is used for calculation every time, the efficiency is very low. Generally speaking, it is "how to kill a chicken with an ox knife".
Since the parameters are updated only a little bit in the opposite direction of the gradient at a time, the direction does not need to be so accurate. A reasonable solution is to randomly extract a small part of data from the total data set each time to represent the whole, and calculate the gradient and loss based on this part of data to update the parameters. This method is called Stochastic Gradient Descent (SGD). The core concepts are as follows:
Mini batch: a batch of data extracted during each iteration is called a mini batch.
batch_size: the number of samples contained in a mini batch is called batch_size.
Epoch: when the program iterates, the samples are gradually extracted by pressing Mini batch. When the entire data set is traversed, a round of training is completed, also known as epoch. When you start training, you can set the number of rounds of training to num_epochs and batch_size is passed in as a parameter.
# get data train_data, test_data = load_data() train_data.shape
train_data contains a total of 404 pieces of data. If batch_size=10, i.e. take the first 0-9 samples as the first mini batch and name it train_data1.
train_data1 = train_data[0:10] train_data1.shape
Using train_ The data of data1 (samples 0-9) calculates the gradient and updates the network parameters.
net = Network(13)
x = train_data1[:, :-1]
y = train_data1[:, -1:]
loss = net.train(x, y, iterations=1, eta=0.01)
loss
According to this method, continuously take out new mini batch and gradually update network parameters.
Next, set train_data is divided into batch in size_ Multiple mini of size_ Batch, as shown in the following code:_ Data is divided into 404 / 10 + 1 = 41 mini_batch, including the first 40 mini_batch, each containing 10 samples, the last mini_batch contains only 4 samples.
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k:k+batch_size] for k in range(0, n, batch_size)]
print('total number of mini_batches is ', len(mini_batches))
print('first mini_batch shape ', mini_batches[0].shape)
print('last mini_batch shape ', mini_batches[-1].shape)
Through a large number of experiments, it is found that the model is more impressed by the last data. After the training data is imported, the closer to the end of model training, the greater the impact of the last few batches of data on model parameters. In order to avoid the influence of model memory on the training effect, it is necessary to operate the samples in disorder.
# Create a new array
a = np.array([1,2,3,4,5,6,7,8,9,10,11,12])
a = a.reshape([6, 2])
print('before shuffle\n', a)
np.random.shuffle(a)
print('after shuffle\n', a)

Observing the running results, it can be found that the elements of the array are randomly disrupted in the 0th dimension, but the order of the 1st dimension remains unchanged. For example, the number 2 is still next to the number 1, the number 8 is still next to the number 7, and the two-dimensional [3,4] is not next to [1,2]. Integrate this part of the code to realize SGD algorithm into the train function in the Network class. The final complete code is as follows.
# get data
train_data, test_data = load_data()
# Disrupt sample order
np.random.shuffle(train_data)
# train_data is divided into multiple mini_batch
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k:k+batch_size] for k in range(0, n, batch_size)]
# Create network
net = Network(13)
# Use each mini in turn_ Batch data
for mini_batch in mini_batches:
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
loss = net.train(x, y, iterations=1)
Key points of modification:
Input each randomly selected Mini batch data into the model for parameter training. The core of the training process is two-level cycle:
The first layer of loop represents that the sample set needs to be trained and traversed several times, which is called "epoch", and the code is as follows:
for epoch_id in range(num_epochs):
The second layer of loop represents the multiple batches of the sample set split into during each traversal, which need to be trained completely. It is called "iter (iteration)", and the code is as follows:
for iter_id,mini_batch in emumerate(mini_batches):
Inside the two-layer loop is a classic four step training process: forward calculation - > calculate loss - > calculate gradient - > update parameters
The final code is as follows:
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# Initial value of randomly generated w
# In order to maintain the consistency of the results of each run of the program, a fixed random number seed is set here
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epochs):
# Shuffle the data before the start of each iteration
# Each time, press batch and then take_ Size data is retrieved in the form of
np.random.shuffle(training_data)
# Split the training data to each mini_batch contains batch_size bar data
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# get data
train_data, test_data = load_data()
# Create network
net = Network(13)
# Start training
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)
# Draw the change trend of the loss function
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
High level API rewriting code of flying slurry
#Load the propeller, Numpy and related class libraries import paddle from paddle.nn import Linear import paddle.nn.functional as F import numpy as np import os import random
Paddle: the main library of the propeller. The aliases of common APIs are reserved in the root directory of paddle, which currently includes: paddle tensor,paddle. All APIs in the framework directory.
paddle.nn: networking related API s, such as Linear, convolution Conv2D, cyclic neural network LSTM, loss function CrossEntropyLoss, activation function ReLU, etc.
Linear: the full connection layer function of neural network, that is, the basic neuron structure containing the addition of all input weights. In the task of house price prediction, only one layer neural network (full connection layer) is used to realize the linear regression model.
paddle.nn.functional: and padding NN, including networking related API s, such as Linear, activation function ReLu, etc. The functions of the modules with the same name under the two are the same, and the operation performance is basically the same. But, paddle The modules under NN are all classes, and each class can have its own module parameters; paddle.nn. All modules under functional are functions, which need to be manually passed into the module to calculate the required parameters. In practical use, convolution, full connection layer and other layers have learnable parameters, and it is recommended to use padding NN module, but the activation function, pooling and other operations have no learnable parameters, so we can consider using the pad directly nn. Function under functional.
data processing
Independent of framework implementation
def load_data():
# Import data from file
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ', dtype=np.float32)
# Each data includes 14 items, of which the first 13 items are influencing factors and the 14th item is the corresponding median house price
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# Reshape the original data into a shape like [N, 14]
data = data.reshape([data.shape[0] // feature_num, feature_num])
# Split the original data set into training set and test set
# Here, 80% of the data are used for training and 20% for testing
# There must be no intersection between training and testing
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# Calculate the maximum, minimum and average values of the train dataset
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# Record the normalization parameters of the data and normalize the data during prediction
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avgs
# Normalize the data
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# Division ratio of training set and test set
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
model design
The essence of model definition is to define the network structure of linear regression. It is suggested that the definition of model network be completed by creating Python class, which needs to inherit the paddle nn. Layer parent class, and define init function and forward function in the class. The forward function is a function specified by the framework to implement the forward calculation logic. The program will automatically execute the forward method when calling the model instance. The network layer used in the forward function needs to be declared in the init function.
The implementation process is divided into the following two steps:
Define init function: declare the implementation function of each layer of network in the initialization function of the class.
Define the forward function: construct the neural network structure, realize the forward calculation process, and return the prediction results. In this task, the house price prediction results are returned.
class Regressor(paddle.nn.Layer):
# self represents the instance of the class itself
def __init__(self):
# Initialize some parameters in the parent class
super(Regressor, self).__init__()
# Define a full connection layer. The input dimension is 13 and the output dimension is 1
self.fc = Linear(in_features=13, out_features=1)
# Forward computing of network
def forward(self, inputs):
x = self.fc(inputs)
return x
Training configuration
1. Declare the defined Regressor instance of the regression model and set the state of the model to training.
2. Use load_ The data function loads training data and test data.
3. Set the optimization algorithm and learning rate. The optimization algorithm adopts random gradient descent SGD, and the learning rate is set to 0.01.
The training configuration code is as follows:
# Declare a well-defined linear regression model model = Regressor() # Open model training mode model.train() # Load data training_data, test_data = load_data() # Define the optimization algorithm and use random gradient descent SGD # The learning rate is set to 0.01 opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
In the case of implementing the neural network model based on Python, we have written a lot of code to realize the gradient descent, while using the propeller framework, we can realize the optimizer setting only by defining SGD, which greatly simplifies the process.
Training process
The training process adopts two-level circular nesting:
Inner loop: it is responsible for one-time traversal of the whole data set, using batch. Assuming that the number of data set samples is 1000 and there are 10 samples in a batch, the number of batches traversing the data set once is 1000 / 10 = 100, that is, the inner loop needs to be executed 100 times.
for iter_id, mini_batch in enumerate(mini_batches):
Outer loop: defines the number of times to traverse the data set through the parameter EPOCH_NUM settings.
for epoch_id in range(EPOCH_NUM):
The value of batch will affect the training effect of the model. If the batch is too large, the memory consumption and calculation time will be increased, and the training effect will not be significantly improved (because each parameter only moves a small step in the opposite direction of the gradient, the direction is not necessary to be particularly accurate); If the batch is too small, the sample data of each batch will have no statistical significance, and the calculated gradient direction may deviate greatly. Since the training data set of house price prediction model is small, we set batch to 10.
EPOCH_NUM = 10 # Sets the number of outer cycles
BATCH_SIZE = 10 # Set batch size
# Define outer loop
for epoch_id in range(EPOCH_NUM):
# Before each iteration, the sequence of training data is randomly disrupted
np.random.shuffle(training_data)
# Split the training data, and each batch contains 10 pieces of data
mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# Define inner loop
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]) # Get training data of current batch
y = np.array(mini_batch[:, -1:]) # Get the training label of the current batch (real house price)
# Convert numpy data into the form of propeller dynamic diagram tensor
house_features = paddle.to_tensor(x)
prices = paddle.to_tensor(y)
# Forward calculation
predicts = model(house_features)
# Calculate loss
loss = F.square_error_cost(predicts, label=prices)
avg_loss = paddle.mean(loss)
if iter_id%20==0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
# Back propagation
avg_loss.backward()
# Minimize loss and update parameters
opt.step()
# Clear gradient
opt.clear_grad()
Save model
# Save the model parameters with the file name LR_model.pdparams
paddle.save(model.state_dict(), 'LR_model.pdparams')
print("The model is saved successfully, and the model parameters are saved in LR_model.pdparams in")
test model
Through load_ one_ The example function extracts a sample from the data set as a test sample. The specific implementation code is as follows.
def load_one_example():
# Randomly select one from the loaded test set above as the test data
idx = np.random.randint(0, test_data.shape[0])
idx = -10
one_data, label = test_data[idx, :-1], test_data[idx, -1]
# Modify the data shape to [1,13]
one_data = one_data.reshape([1,-1])
return one_data, label
# The parameter is the file address where the model parameters are saved
model_dict = paddle.load('LR_model.pdparams')
model.load_dict(model_dict)
model.eval()
# The parameter is the file address of the dataset
one_data, label = load_one_example()
# Convert data to variable format of dynamic graph
one_data = paddle.to_tensor(one_data)
predict = model(one_data)
# The results are inverse normalized
predict = predict * (max_values[-1] - min_values[-1]) + avg_values[-1]
# Inverse normalization of label data
label = label * (max_values[-1] - min_values[-1]) + avg_values[-1]
print("Inference result is {}, the corresponding label is {}".format(predict.numpy(), label))