1, Title Requirements
- Given a two-dimensional binary matrix containing only 0 and 1 and the size of rows x cols, find the largest rectangle containing only 1 and return its area.
- Example 1:
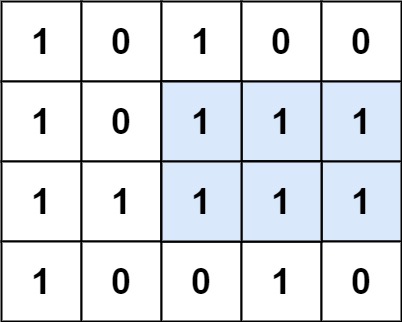
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Input: matrix = []
Output: 0
Input: matrix = [["0"]]
Output: 0
Input: matrix = [["1"]]
Output: 1
Input: matrix = [["0","0"]]
Output: 0
- Tips:
-
-
- cols == matrix[0].length;
-
-
- matrix[i][j] is' 0 'or' 1 '.
2, Solving algorithm
① Brute force cracking
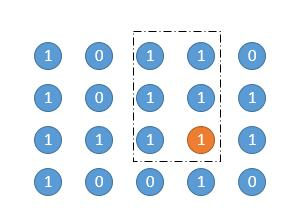
- Traverse each point and find all matrix areas with this point as the lower right corner of the matrix. As shown below, orange is the currently traversed point, and then the matrix circled by the dotted box is one of them:
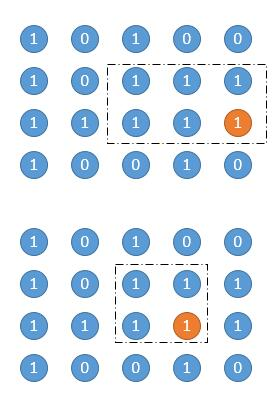
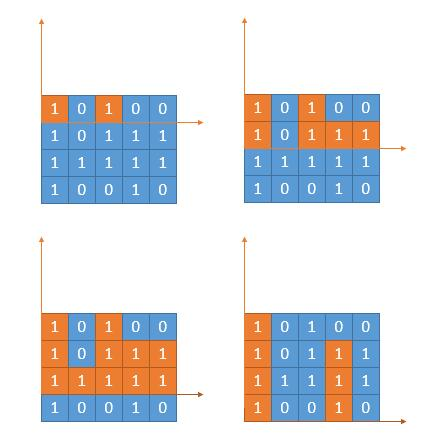
- How to find such a matrix? As shown below, if you know the number of consecutive ones ending at this point, the problem becomes simple:
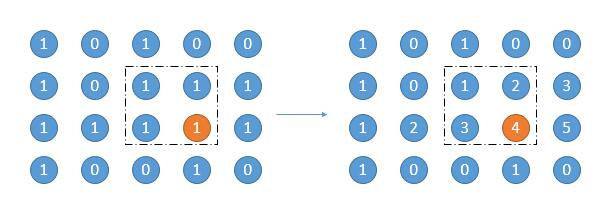
- Specific steps:
-
- A. First, find the rectangular area with height of 1, that is, its own number, such as orange 4 in the above figure, and the area is 4.
-
- B. Then expand a row upward, increase the height by one, select the smallest number in the current column as the width of the matrix, and calculate the area, corresponding to the rectangular box in the figure above.
-
- C. Then continue to expand upward and repeat step B.
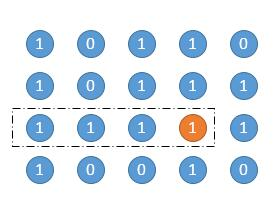
- According to the above method, traverse all points and find all matrices.
- Take the orange point as the lower right corner:
-

public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0) {
return 0;
}
// Saves the number of consecutive ones ending with the current number
int[][] width = new int[matrix.length][matrix[0].length];
int maxArea = 0;
// Traverse each line
for (int row = 0; row < matrix.length; row++) {
for (int col = 0; col < matrix[0].length; col++) {
// Update width
if (matrix[row][col] == '1') {
if (col == 0) {
width[row][col] = 1;
} else {
width[row][col] = width[row][col - 1] + 1;
}
} else {
width[row][col] = 0;
}
// Record the minimum number of all rows
int minWidth = width[row][col];
// Expand row up
for (int up_row = row; up_row >= 0; up_row--) {
int height = row - up_row + 1;
// Find the smallest number as the width of the matrix
minWidth = Math.min(minWidth, width[up_row][col]);
// Renewal area
maxArea = Math.max(maxArea, height * minWidth);
}
}
}
return maxArea;
}
② Stack
- It's not hard to think of it. Just find the heights [] of each layer and pass it to the function of the previous question.
- Java example:
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0) {
return 0;
}
int[] heights = new int[matrix[0].length];
int maxArea = 0;
for (int row = 0; row < matrix.length; row++) {
// Traverse each column and update the height
for (int col = 0; col < matrix[0].length; col++) {
if (matrix[row][col] == '1') {
heights[col] += 1;
} else {
heights[col] = 0;
}
}
// Update function
maxArea = Math.max(maxArea, largestRectangleArea(heights));
}
return maxArea;
}
public int largestRectangleArea(int[] heights) {
int maxArea = 0;
Stack<Integer> stack = new Stack<>();
int p = 0;
while (p < heights.length) {
// Stack empty stack
if (stack.isEmpty()) {
stack.push(p);
p++;
} else {
int top = stack.peek();
// The current height is greater than the top of the stack, and the stack
if (heights[p] >= heights[top]) {
stack.push(p);
p++;
} else {
// Save stack top height
int height = heights[stack.pop()];
// The first one on the left is smaller than the subscript of the current column
int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
// The first one on the right is smaller than the subscript of the current column
int RightLessMin = p;
// Calculated area
int area = (RightLessMin - leftLessMin - 1) * height;
maxArea = Math.max(area, maxArea);
}
}
}
while (!stack.isEmpty()) {
// Save stack top height
int height = heights[stack.pop()];
// The first one on the left is smaller than the subscript of the current column
int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
// There is no column less than the current height on the right, so it is assigned as the length of the array for easy calculation
int RightLessMin = heights.length;
int area = (RightLessMin - leftLessMin - 1) * height;
maxArea = Math.max(area, maxArea);
}
return maxArea;
}
③ Dynamic programming
- In solution ②, update the heights once, use the previous algorithm to find leftLessMin [] and rightLessMin [], and then update the area. In fact, leftLessMin [] and rightLessMin [] can be updated by using the previous leftLessMin [] and rightLessMin [].
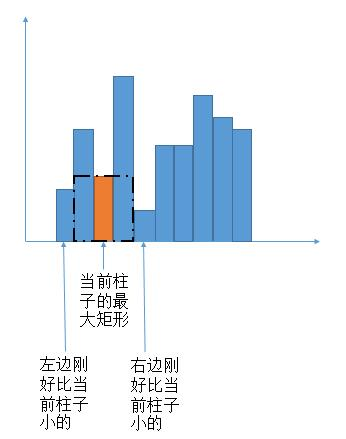
- Recall the meanings of leftLessMin [] and rightLessMin []. leftLessMin [i] represents the first subscript on the left that is lower than the current column, as shown in the following figure. When the orange column is the current traversed column, rightLessMin [] is the first on the right:
- Left and right are symmetrical relations. Only the solution of left is considered below. As shown in the following figure, if all the newly added layers are 1, of course, this is the most perfect case, then leftLessMin [] does not need to be changed at all:
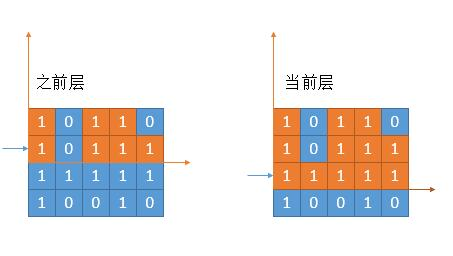
- However, the fact is cruel. There must be 0:
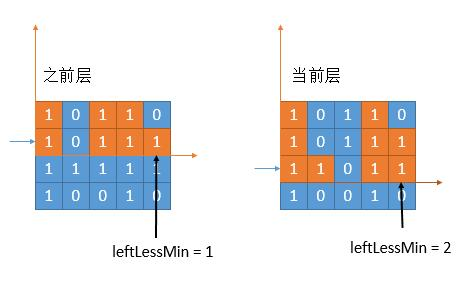
- Considering the update of the last column, leftLessMin = 1 on the upper floor, that is, the position of blue 0 is the first column lower than it. However, in the current layer, 0 appears in the middle. Therefore, it is no longer the previous leftLessMin, but compared with the position where 0 appeared last time (because 0 must be smaller than the current column). Whoever has a larger subscript and is closer to the current column will be selected. The position of 0 in the above figure is 2, and the previous leftLessMin is 1. Choose a larger one, that is 2.
- Java example:
public int maximalRectangle4(char[][] matrix) {
if (matrix.length == 0) {
return 0;
}
int maxArea = 0;
int cols = matrix[0].length;
int[] leftLessMin = new int[cols];
int[] rightLessMin = new int[cols];
// Initialize to - 1, that is, the leftmost
Arrays.fill(leftLessMin, -1);
// Initialize to cols, that is, the rightmost
Arrays.fill(rightLessMin, cols);
int[] heights = new int[cols];
for (int row = 0; row < matrix.length; row++) {
// Update all heights
for (int col = 0; col < cols; col++) {
if (matrix[row][col] == '1') {
heights[col] += 1;
} else {
heights[col] = 0;
}
}
// Update all leftLessMin
int boundary = -1; // Record the last occurrence of 0
for (int col = 0; col < cols; col++) {
if (matrix[row][col] == '1') {
// Compare with the last occurrence of 0
leftLessMin[col] = Math.max(leftLessMin[col], boundary);
} else {
// Currently 0 means the current height is 0, so it is initialized to - 1 to prevent the impact on the next cycle
leftLessMin[col] = -1;
// Update the location of 0
boundary = col;
}
}
// The same is true on the right
boundary = cols;
for (int col = cols - 1; col >= 0; col--) {
if (matrix[row][col] == '1') {
rightLessMin[col] = Math.min(rightLessMin[col], boundary);
} else {
rightLessMin[col] = cols;
boundary = col;
}
}
// Update all areas
for (int col = cols - 1; col >= 0; col--) {
int area = (rightLessMin[col] - leftLessMin[col] - 1) * heights[col];
maxArea = Math.max(area, maxArea);
}
}
return maxArea;
}









