Catalogue
2) Application of Hamming distance
3, Geometric significance and principle of SimHash algorithm
1) Geometric significance of SimHash algorithm
2) Calculation principle of SimHash
III) text similarity calculation
4, Java calculates text content similarity through SimHash code example
3) Calculate the Hash value of a single participle
4) . word segmentation calculation vector
5) . get Hamming distance of title content
6) . obtain the similarity of title content
1, Foreword
In the process of project development, there is a need to calculate the similarity of texts from a large number of texts and classify them. The general practice is to compare the similarity in pairs, but this pair of similarity calculation algorithms takes a long time. Once the amount of data is huge, it can be effective immediately. Er, compared with pairing, this may not be suitable for projects or products. It's OK to play. If we encounter a large number of texts, we should quickly and efficiently calculate the similarity of texts and classify them. How can we achieve it? This is what bloggers in this article need to express.
Through the study of this paper, it will be easy to understand and realize the similarity calculation between a large number of texts. In this paper, the blogger realizes the calculation of help similarity through SimHash algorithm and combined with the actual code. Of course, the classification needs to be divided according to the specific needs. As long as the similarity is calculated, the rest is simple.
2, About SimHash
SimHash algorithm is a fingerprint generation algorithm mentioned in the paper "detecting near duplicates for web crawling" published by Google in 2007. It is applied in the work of page de duplication of Google search engine. The SimHash value not only provides information about whether the original values are equal, but also calculates the difference degree of the content.
In short, the main work of SimHash algorithm is to reduce the dimension of the text and generate a SimHash value, that is, the "fingerprint" mentioned in the paper. By comparing the SimHash values of different texts and then comparing the "Hamming distance", we can judge the similarity between the two texts.
For the problem of text similarity, common solutions include European distance, editing distance, longest common substring, cosine algorithm, Jaccard similarity and so on. However, these methods can not deal with massive data efficiently.
For example, in search engines, there are many similar keywords. The content users need to obtain is similar, but the search keywords are different, for example:
"What are the cold knowledge that cats must know?"
"What cold knowledge do cats have to know?"
The above two keywords can be equivalent. However, through ordinary hash calculation, two hash strings will be generated. The hash string calculated by SimHash will be very similar, so we can judge the similarity of the two texts.
Supplementary knowledge
1) What is Hamming distance
Hamming distance is one of the editing distances. In information coding, the number of different bits encoded on the corresponding bits of two legal codes is called code distance, also known as Hamming distance. That is, the number of bits with different values of the corresponding bits of the two codewords is called the Hamming distance of the two codewords. The minimum Hamming distance of any two codewords in an effective coding set is called the Hamming distance of the coding set. For example, if 10101 and 00110 are different from the first, fourth and fifth positions, the Hamming distance is 3.
The N-bit codeword can be represented by a vertex of the hypercube in N-dimensional space. The Hamming distance between two codewords is an edge between the two vertices of the hypercube, and it is the shortest distance between the two vertices.
2) Application of Hamming distance
Hamming distance is most widely used in massive essays and text de duplication, which is characterized by its excellent performance. Hamming distance is mainly to vectorize the text, or extract the features of the text and map them into coding, and then XOR the coding to calculate the Hamming distance.
3) What is edit distance
Editing distance, also known as Levenshtein Distance (also known as Edit Distance), refers to the minimum number of editing operations required to convert one character into another between two strings. The allowable editing operations include replacing one character with another, inserting one character and deleting one character.
3, Geometric significance and principle of SimHash algorithm
1) Geometric significance of SimHash algorithm
Firstly, it maps each feature into a vector in f-dimensional space. The specific mapping rule is not important, as long as for many different features, their corresponding vectors are evenly and randomly distributed, and the corresponding vectors are unique for the same features. For example, the binary representation of a 4-bit Hash signature of a feature is 1010, then the 4-dimensional vector corresponding to this feature is (1,-1,1,-1)T, that is, a bit of the Hash signature is 1, and the corresponding bit of the mapped vector is 1, otherwise it is - 1. Then, the vectors corresponding to each feature contained in a document are weighted and summed, and the weighted coefficient is equal to the weight of the feature. The resulting sum vector represents the document. We can use the included angle between vectors to measure the similarity between corresponding documents. Finally, in order to obtain an F-bit signature, it needs to be further compressed. If one dimension of the sum vector is greater than 0, the corresponding bit of the final signature is 1, otherwise it is 0. Such compression is equivalent to leaving only the information of the quadrant where the sum vector is located, and the 64 bit signature can represent up to 264 quadrants, so saving only the information of the quadrant is enough to represent a document.
The geometric meaning of SimHash algorithm is clarified, which makes the algorithm intuitively reasonable. However, why is the similarity of the final signature, that is, the similarity of the original document can be measured. The specific SimHash algorithm and proof are not given in the paper of Charikar, the inventor of SimHash. The proof ideas are listed below:
SimHash is evolved from the random hyperplane Hash algorithm. The random hyperplane Hash algorithm is very simple. For an n-dimensional vector v, to obtain an F-bit signature (f < < n), the algorithm is as follows:
1. Randomly generate f n-dimensional vectors r1,... rf;
2. For each vector ri, if the dot product of v and ri is greater than 0, the i-th bit of the final signature is 1, otherwise it is 0;
This algorithm is equivalent to randomly generating f n-dimensional hyperplanes. Each hyperplane divides the space of vector v into two. v gets a 1 above this hyperplane, otherwise it gets a 0, and then combines the obtained f zeros or 1 to form an f-dimensional signature. If the angle between two vectors u and v is θ, Then the probability of a random hyperplane separating them is θ/ π. Therefore, the probability that the corresponding bits of the signatures of u and v are different is equal to θ/ π. Therefore, we can use the number of different corresponding bits of the signatures of the two vectors, that is, Hamming distance, to measure the difference between the two vectors.
How does SimHash algorithm relate to random hyperplane hash? In the SimHash algorithm, the random vector used to divide the space is not directly generated, but the ith bit of the hash signature with - > the k-th feature is indirectly generated. If it is 0, it will be changed to - 1. If it is 1, it will remain unchanged as the k-th dimension of the i-th random vector. Since the hash signature is F-bit, it can generate f random vectors corresponding to f random hyperplanes. Here is an example:
Suppose that all documents are represented by five features w1,..., w5. Now we want to get a three-dimensional signature of any document.
Assume that the three-dimensional vectors corresponding to these five features are:
h(w1) = (1, -1, 1)T
h(w2) = (-1, 1, 1)T
h(w3) = (1, -1, -1)T
h(w4) = (-1, -1, 1)T
h(w5) = (1, 1, -1)T
According to SimHash algorithm, we need to get a document vector
For the signature of d=(w1=1, w2=2, w3=0, w4=3, w5=0) T, the vector must be calculated first
m = 1*h(w1) + 2*h(w2) + 0*h(w3) + 3*h(w4) + 0*h(w5) = (-4, -2, 6) T,
Then, according to step 3 of SimHash algorithm, the final signature s=001 is obtained.
The above calculation steps are actually equivalent to - > get three 5-Dimensional vectors first:
The first 5-Dimensional vector consists of the first dimension of h(w1),..., h(w5): r1=(1,-1,1,-1,1) T;
The second 5-Dimensional vector consists of the second dimension of h(w1),..., h(w5): r2=(-1,1,-1,-1,1) T;
The third 5-Dimensional vector consists of the third dimension of h(w1),..., h(w5): r3=(1,1,-1,1,-1) T;
According to step 2 of the random hyperplane algorithm, calculate the dot product of vector d and R1, R2 and R3 respectively:
D t R1 = - 4 < 0, so s1=0;
D t R2 = - 2 < 0, so s2=0;
D t R3 = 6 > 0, so s3=1;
Therefore, the final signature s=001 is consistent with the result produced by SimHash algorithm.
From the above calculation process, it can be seen that SimHash algorithm is actually the same as random hyperplane Hash algorithm. The Hamming distance of two signatures obtained by SimHash algorithm can be used to measure the included angle of the original vector. This is actually a dimensionality reduction technique, which characterizes high-dimensional vectors with lower dimensional signatures. To measure the similarity of two contents, Hamming distance needs to be calculated, which brings some computational difficulties to the application of finding similar contents with a given signature.
The input of SimHash algorithm is a vector and the output is an f-bit signature value. For ease of expression, suppose that the input is a feature set of a document, and each feature has a certain weight. For example, the feature can be a word in the document, and its weight can be the number of times the word appears.
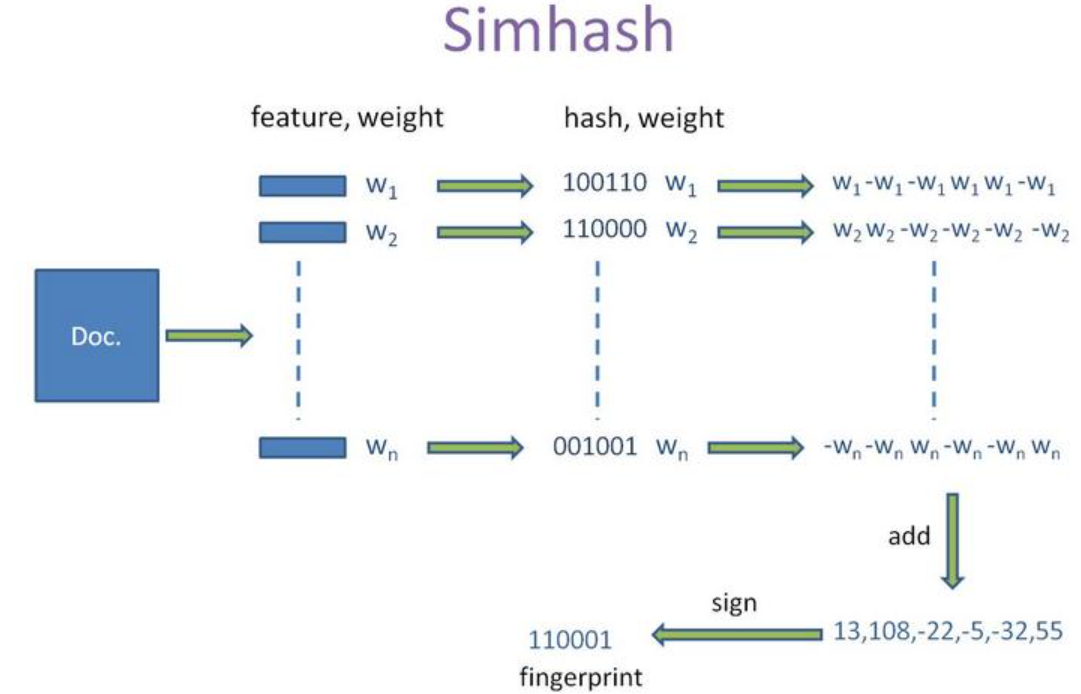
2) Calculation principle of SimHash
SimHash algorithm is mainly divided into five processes: word segmentation, Hash, weighting, merging and dimension reduction. As shown in Figure example [illustration-01]
1. Participle
A given piece of text is segmented to produce n feature words, and each feature word is given a weight.
2.Hash
Each word vector is mapped by hash function to produce an n-bit binary string.
3. Weighting
After the previous calculation, the Hash string of each word vector and the weight corresponding to the word vector have been obtained. In the third step, calculate the weight vector W=hash*weight.
4. Consolidation
For a text, the weight vector of each feature word after text word segmentation is calculated. In the merging stage, the weight vectors of all word vectors of the text are accumulated to obtain a new weight vector.
5. Dimensionality reduction
For the weight vector of the previously merged text, the SimHash value of the text can be obtained if the position is 1 greater than 0 and 0 less than or equal to 0.
The steps of SimHash algorithm are as follows:
1. Initialize a vector V of f dimension to 0; The binary number S of f bits is initialized to 0;
2. For each feature, the traditional Hash algorithm is used to generate an f-bit signature b. For i=1 to f:
If the ith bit of b is 1, the ith element of V plus the weight of the feature;
Otherwise, the i-th element of V subtracts the weight of the feature;
3. If the ith element of V is greater than 0, the ith bit of S is 1, otherwise it is 0;
4. Output S as signature;
The schematic diagram of Simhash algorithm is as follows:
III) text similarity calculation
For each text, calculate the signature according to SimHash, and then calculate the Hamming distance of two signatures (the number of 1 after two binary XORs). According to the empirical value, for 64 bit SimHash, if the Hamming distance is less than 3, it can be considered that the similarity is relatively high.
Suppose that for 64 bit SimHash, find all signatures with Hamming distance less than 3. The 64 bit binary signature can be divided into 4 blocks, 16 bits each. According to the pigeon nest principle (also known as the drawer principle, see Combinatorial Mathematics), if the Hamming distance of two signatures is within 3, they must have exactly the same piece.
Take each of the four blocks divided above as the first 16 bits to search. Establish inverted index.
The schematic diagram of similarity algorithm is as follows:
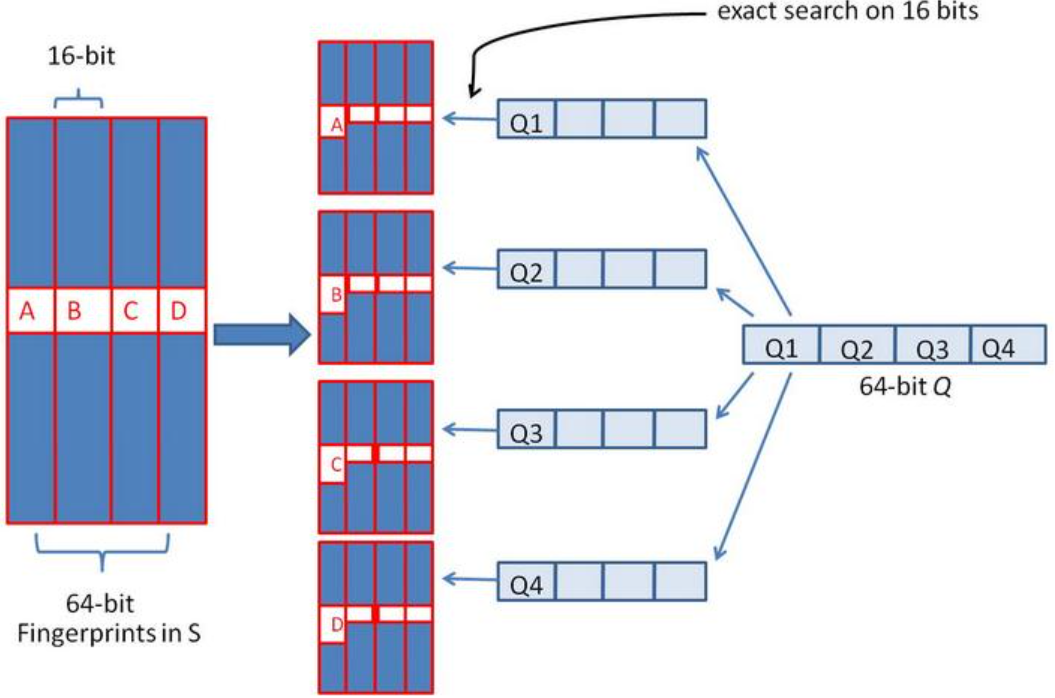
If there are 2 ^ 34 (about 1 billion) signatures in the library, the maximum number of matching results for each block is 2 ^ (34-16) = 262144 candidate results (assuming that the data is evenly distributed and the 16 bit data produces 2 ^ 16 image limits, the average number of documents per image limit distribution is 2 ^ 34 / 2 ^ 16 = 2 ^ (34-16)), and the total number of returned results from the four blocks is 4 * 262144 (about 1 million). Originally, it needs to be compared 1 billion times. After indexing, it only needs to be processed 1 million times. It can be seen that the amount of calculation is greatly reduced
4, Java calculates text content similarity through SimHash code example
1) . add dependent packages
<dependency>
<groupId>org.jsoup</groupId>
<artifactId>jsoup</artifactId>
<version>1.11.3</version>
</dependency>
<dependency>
<groupId>com.hankcs</groupId>
<artifactId>hanlp</artifactId>
<version>portable-1.8.1</version>
</dependency>
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-lang3</artifactId>
<version>3.11</version>
</dependency>2) Special characters
/**
* Description:[Filter special characters]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private String clearSpecialCharacters(String topicName) {
// Convert content to lowercase
topicName = StringUtils.lowerCase(topicName);
// Come here HTML tags
topicName = Jsoup.clean(topicName, Whitelist.none());
// Filter special characters
String[] strings = {" ", "\n", "\r", "\t", "\\r", "\\n", "\\t", " ", "&", "<", ">", """, "&qpos;"};
for (String string : strings) {
topicName = topicName.replaceAll(string, "");
}
return topicName;
}3) Calculate the Hash value of a single participle
/**
* Description:[Calculate hash value of single participle]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private BigInteger getWordHash(String word) {
if (StringUtils.isEmpty(word)) {
// If the participle is null, the default hash is 0
return new BigInteger("0");
} else {
// Word segmentation and place filling, if too short, will lead to the failure of Hash algorithm
while (word.length() < SimHashUtil.WORD_MIN_LENGTH) {
word = word + word.charAt(0);
}
// Participle operation
char[] wordArray = word.toCharArray();
BigInteger x = BigInteger.valueOf(wordArray[0] << 7);
BigInteger m = new BigInteger("1000003");
// Initial bucket pow operation
BigInteger mask = new BigInteger("2").pow(this.hashCount).subtract(new BigInteger("1"));
for (char item : wordArray) {
BigInteger temp = BigInteger.valueOf(item);
x = x.multiply(m).xor(temp).and(mask);
}
x = x.xor(new BigInteger(String.valueOf(word.length())));
if (x.equals(ILLEGAL_X)) {
x = new BigInteger("-2");
}
return x;
}
}4) . word segmentation calculation vector
/**
* Description:[Word segmentation calculation vector]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private BigInteger simHash() {
// Clear special characters
this.topicName = this.clearSpecialCharacters(this.topicName);
int[] hashArray = new int[this.hashCount];
// Word segmentation of content
List<Term> terms = StandardTokenizer.segment(this.topicName);
// Configure part of speech weight
Map<String, Integer> weightMap = new HashMap<>(16, 0.75F);
weightMap.put("n", 1);
// Set stop words
Map<String, String> stopMap = new HashMap<>(16, 0.75F);
stopMap.put("w", "");
// Set overclocking words online
Integer overCount = 5;
// Set word segmentation statistics
Map<String, Integer> wordMap = new HashMap<>(16, 0.75F);
for (Term term : terms) {
// Get word segmentation string
String word = term.word;
// Get participle part of speech
String nature = term.nature.toString();
// Filter overclocking words
if (wordMap.containsKey(word)) {
Integer count = wordMap.get(word);
if (count > overCount) {
continue;
} else {
wordMap.put(word, count + 1);
}
} else {
wordMap.put(word, 1);
}
// Filter stop words
if (stopMap.containsKey(nature)) {
continue;
}
// Calculate the Hash value of a single participle
BigInteger wordHash = this.getWordHash(word);
for (int i = 0; i < this.hashCount; i++) {
// Vector displacement
BigInteger bitMask = new BigInteger("1").shiftLeft(i);
// Judge the column after each word segmentation hash, for example: 1000 1, the first and last bits of the array will be added with 1, and the middle 62 bits will be subtracted by 1, that is, every 1 will be added with 1, and every 0 will be subtracted with 1, until all participle hash columns are judged
// Set initial weight
Integer weight = 1;
if (weightMap.containsKey(nature)) {
weight = weightMap.get(nature);
}
// Calculate the vector of all participles
if (wordHash.and(bitMask).signum() != 0) {
hashArray[i] += weight;
} else {
hashArray[i] -= weight;
}
}
}
// Generate fingerprint
BigInteger fingerPrint = new BigInteger("0");
for (int i = 0; i < this.hashCount; i++) {
if (hashArray[i] >= 0) {
fingerPrint = fingerPrint.add(new BigInteger("1").shiftLeft(i));
}
}
return fingerPrint;
}5) . get Hamming distance of title content
/**
* Description:[Get Hamming distance of title content]
*
* @return Double
* @date 2020-04-01
* @author huazai
*/
private int getHammingDistance(SimHashUtil simHashUtil) {
// Difference set
BigInteger subtract = new BigInteger("1").shiftLeft(this.hashCount).subtract(new BigInteger("1"));
// Seek differences or
BigInteger xor = this.bigSimHash.xor(simHashUtil.bigSimHash).and(subtract);
int total = 0;
while (xor.signum() != 0) {
total += 1;
xor = xor.and(xor.subtract(new BigInteger("1")));
}
return total;
}6) . obtain the similarity of title content
/**
* Description:[Get the similarity of title content]
*
* @return Double
* @date 2020-04-01
* @author huazai
*/
public Double getSimilar(SimHashUtil simHashUtil) {
// Get Hamming distance
Double hammingDistance = (double) this.getHammingDistance(simHashUtil);
// Find Hamming distance percentage
Double scale = (1 - hammingDistance / this.hashCount) * 100;
Double formatScale = Double.parseDouble(String.format("%.2f", scale));
return formatScale;
}7) , test
public static void main(String[] args) {
// Prepare test title content data
List<String> titleList = new ArrayList<>();
titleList.add("What cold knowledge do cats have to know");
titleList.add("What must cats know about cold weather");
titleList.add("What must cats know");
titleList.add("Who keeps cats");
titleList.add("What are there");
// Original data title
String originalTitle = "What cold knowledge do cats have to know?";
Map<String, Double> simHashMap = new HashMap<>(16, 0.75F);
System.out.println("======================================");
long startTime = System.currentTimeMillis();
System.out.println("Original title:" + originalTitle);
// Calculate similarity
titleList.forEach(title -> {
SimHashUtil mySimHash_1 = new SimHashUtil(title, 64);
SimHashUtil mySimHash_2 = new SimHashUtil(originalTitle, 64);
Double similar = mySimHash_1.getSimilar(mySimHash_2);
simHashMap.put(title, similar);
});
// Print test results to console
/* simHashMap.forEach((title, similarity) -> {
System.out.println("Title: "+ title +" ----------------- similarity: "+ similarity);
});*/
// Sort output console by title content
Set<String> titleSet = simHashMap.keySet();
Object[] titleArrays = titleSet.toArray();
Arrays.sort(titleArrays, Collections.reverseOrder());
System.out.println("-------------------------------------");
for (Object title : titleArrays) {
System.out.println("title:" + title + "-----------Similarity:" + simHashMap.get(title));
}
// Calculation duration (unit: ms)
long endTime = System.currentTimeMillis();
long totalTime = endTime - startTime;
System.out.println("\n Total time of this operation" + totalTime + "millisecond");
System.out.println("======================================");
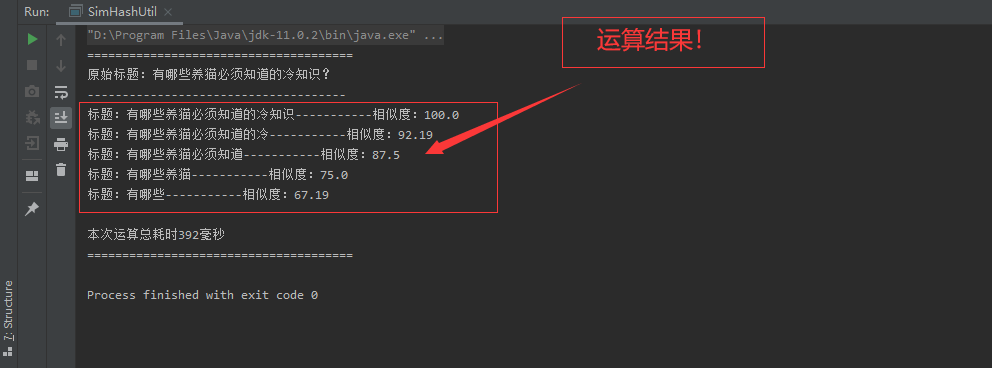
}8) . example renderings
9) Complete code example
package com.b2c.aiyou.bbs.common.utils.hanlp;
import com.hankcs.hanlp.seg.common.Term;
import com.hankcs.hanlp.tokenizer.StandardTokenizer;
import org.apache.commons.lang3.StringUtils;
import org.jsoup.Jsoup;
import org.jsoup.safety.Whitelist;
import java.math.BigInteger;
import java.util.*;
/**
* System: BBS Forum system
* Department: R & D group 1
* Title: [aiyou-bbs — SimHashUtil [module]
* Description: [SimHash Title content similarity algorithm tool class]
* Created on: 2020-04-01
* Contacts: [who.seek.me@java98k.vip]
*
* @author huazai
* @version V1.1.0
*/
public class SimHashUtil {
/**
* Title name
*/
private String topicName;
/**
* Word segmentation vector
*/
private BigInteger bigSimHash;
/**
* Initial bucket size
*/
private Integer hashCount = 64;
/**
* Minimum length limit of word segmentation
*/
private static final Integer WORD_MIN_LENGTH = 3;
private static final BigInteger ILLEGAL_X = new BigInteger("-1");
public SimHashUtil(String topicName, Integer hashCount) {
this.topicName = topicName;
this.bigSimHash = this.simHash();
this.hashCount = hashCount;
}
/**
* Description:[Word segmentation calculation vector]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private BigInteger simHash() {
// Clear special characters
this.topicName = this.clearSpecialCharacters(this.topicName);
int[] hashArray = new int[this.hashCount];
// Word segmentation of content
List<Term> terms = StandardTokenizer.segment(this.topicName);
// Configure part of speech weight
Map<String, Integer> weightMap = new HashMap<>(16, 0.75F);
weightMap.put("n", 1);
// Set stop words
Map<String, String> stopMap = new HashMap<>(16, 0.75F);
stopMap.put("w", "");
// Set overclocking words online
Integer overCount = 5;
// Set word segmentation statistics
Map<String, Integer> wordMap = new HashMap<>(16, 0.75F);
for (Term term : terms) {
// Get word segmentation string
String word = term.word;
// Get participle part of speech
String nature = term.nature.toString();
// Filter overclocking words
if (wordMap.containsKey(word)) {
Integer count = wordMap.get(word);
if (count > overCount) {
continue;
} else {
wordMap.put(word, count + 1);
}
} else {
wordMap.put(word, 1);
}
// Filter stop words
if (stopMap.containsKey(nature)) {
continue;
}
// Calculate the Hash value of a single participle
BigInteger wordHash = this.getWordHash(word);
for (int i = 0; i < this.hashCount; i++) {
// Vector displacement
BigInteger bitMask = new BigInteger("1").shiftLeft(i);
// Judge the column after each word segmentation hash, for example: 1000 1, the first and last bits of the array will be added with 1, and the middle 62 bits will be subtracted by 1, that is, every 1 will be added with 1, and every 0 will be subtracted with 1, until all participle hash columns are judged
// Set initial weight
Integer weight = 1;
if (weightMap.containsKey(nature)) {
weight = weightMap.get(nature);
}
// Calculate the vector of all participles
if (wordHash.and(bitMask).signum() != 0) {
hashArray[i] += weight;
} else {
hashArray[i] -= weight;
}
}
}
// Generate fingerprint
BigInteger fingerPrint = new BigInteger("0");
for (int i = 0; i < this.hashCount; i++) {
if (hashArray[i] >= 0) {
fingerPrint = fingerPrint.add(new BigInteger("1").shiftLeft(i));
}
}
return fingerPrint;
}
/**
* Description:[Calculate hash value of single participle]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private BigInteger getWordHash(String word) {
if (StringUtils.isEmpty(word)) {
// If the participle is null, the default hash is 0
return new BigInteger("0");
} else {
// Word segmentation and place filling, if too short, will lead to the failure of Hash algorithm
while (word.length() < SimHashUtil.WORD_MIN_LENGTH) {
word = word + word.charAt(0);
}
// Participle operation
char[] wordArray = word.toCharArray();
BigInteger x = BigInteger.valueOf(wordArray[0] << 7);
BigInteger m = new BigInteger("1000003");
// Initial bucket pow operation
BigInteger mask = new BigInteger("2").pow(this.hashCount).subtract(new BigInteger("1"));
for (char item : wordArray) {
BigInteger temp = BigInteger.valueOf(item);
x = x.multiply(m).xor(temp).and(mask);
}
x = x.xor(new BigInteger(String.valueOf(word.length())));
if (x.equals(ILLEGAL_X)) {
x = new BigInteger("-2");
}
return x;
}
}
/**
* Description:[Filter special characters]
*
* @return BigInteger
* @date 2020-04-01
* @author huazai
*/
private String clearSpecialCharacters(String topicName) {
// Convert content to lowercase
topicName = StringUtils.lowerCase(topicName);
// Come here HTML tags
topicName = Jsoup.clean(topicName, Whitelist.none());
// Filter special characters
String[] strings = {" ", "\n", "\r", "\t", "\\r", "\\n", "\\t", " ", "&", "<", ">", """, "&qpos;"};
for (String string : strings) {
topicName = topicName.replaceAll(string, "");
}
return topicName;
}
/**
* Description:[Get the similarity of title content]
*
* @return Double
* @date 2020-04-01
* @author huazai
*/
public Double getSimilar(SimHashUtil simHashUtil) {
// Get Hamming distance
Double hammingDistance = (double) this.getHammingDistance(simHashUtil);
// Find Hamming distance percentage
Double scale = (1 - hammingDistance / this.hashCount) * 100;
Double formatScale = Double.parseDouble(String.format("%.2f", scale));
return formatScale;
}
/**
* Description:[Get Hamming distance of title content]
*
* @return Double
* @date 2020-04-01
* @author huazai
*/
private int getHammingDistance(SimHashUtil simHashUtil) {
// Difference set
BigInteger subtract = new BigInteger("1").shiftLeft(this.hashCount).subtract(new BigInteger("1"));
// Seek differences or
BigInteger xor = this.bigSimHash.xor(simHashUtil.bigSimHash).and(subtract);
int total = 0;
while (xor.signum() != 0) {
total += 1;
xor = xor.and(xor.subtract(new BigInteger("1")));
}
return total;
}
}
5, Concluding remarks
That's all for SimHash algorithm to calculate text similarity. Of course, interested partners can also try the performance of cosine algorithm, Euclidean distance and Hamming distance in text similarity calculation,
Examples of test performance:
Calculation performance value ratio of 10W text;
Calculation performance value ratio of 1000W text;
Calculation performance value ratio of 3000W text;
Calculation performance value ratio of 5000W text;
reference:
Well, about Java's Title Similarity Calculation and text content similarity matching, Java calculates the title text content similarity through SimHash. If you have any questions or encounter any problems, please scan the code and ask questions. You can also leave me a message. I will answer them in detail one by one.
Xiehouyu: "learn together and make progress together". I also hope you will pay more attention to the IT community of CSND.
| Author: | Hua Zi |
| Contact author: | who.seek.me@java98k.vip |
| Source: | CSDN (Chinese Software Developer Network) |
| Original: | https://blog.csdn.net/Hello_World_QWP/article/details/122842339 |
| Copyright notice: | This article is the original article of the blogger. Please indicate the source of the blog when reprinting! |