support vector machine
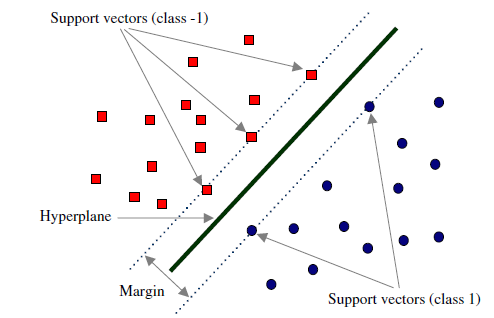
In the case of linear separability, the data point closest to the separation hyperplane in the sample points of the training data set is called support vector.
The cost function and logistic regression are similar:

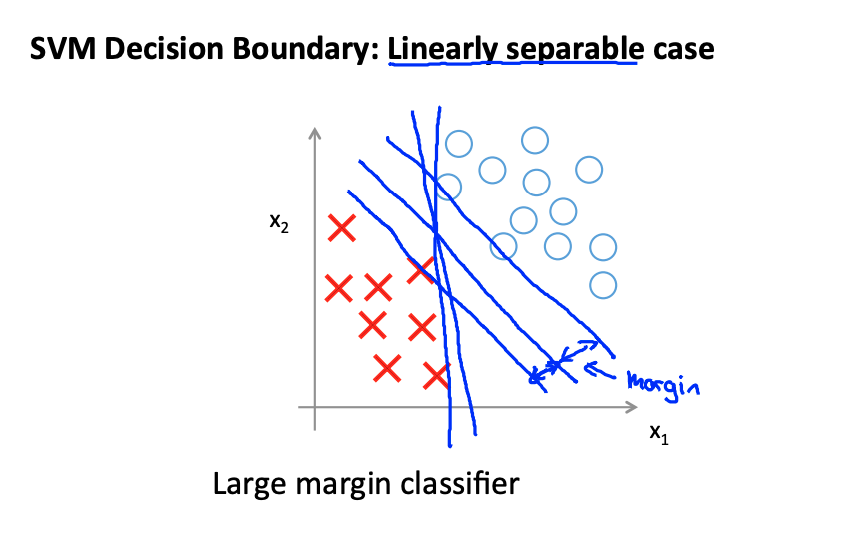
Also known as large interval classifier, it can find the best linear classification position:
The physical meaning of vector inner product is equivalent to the product of the projection length of one vector on another:
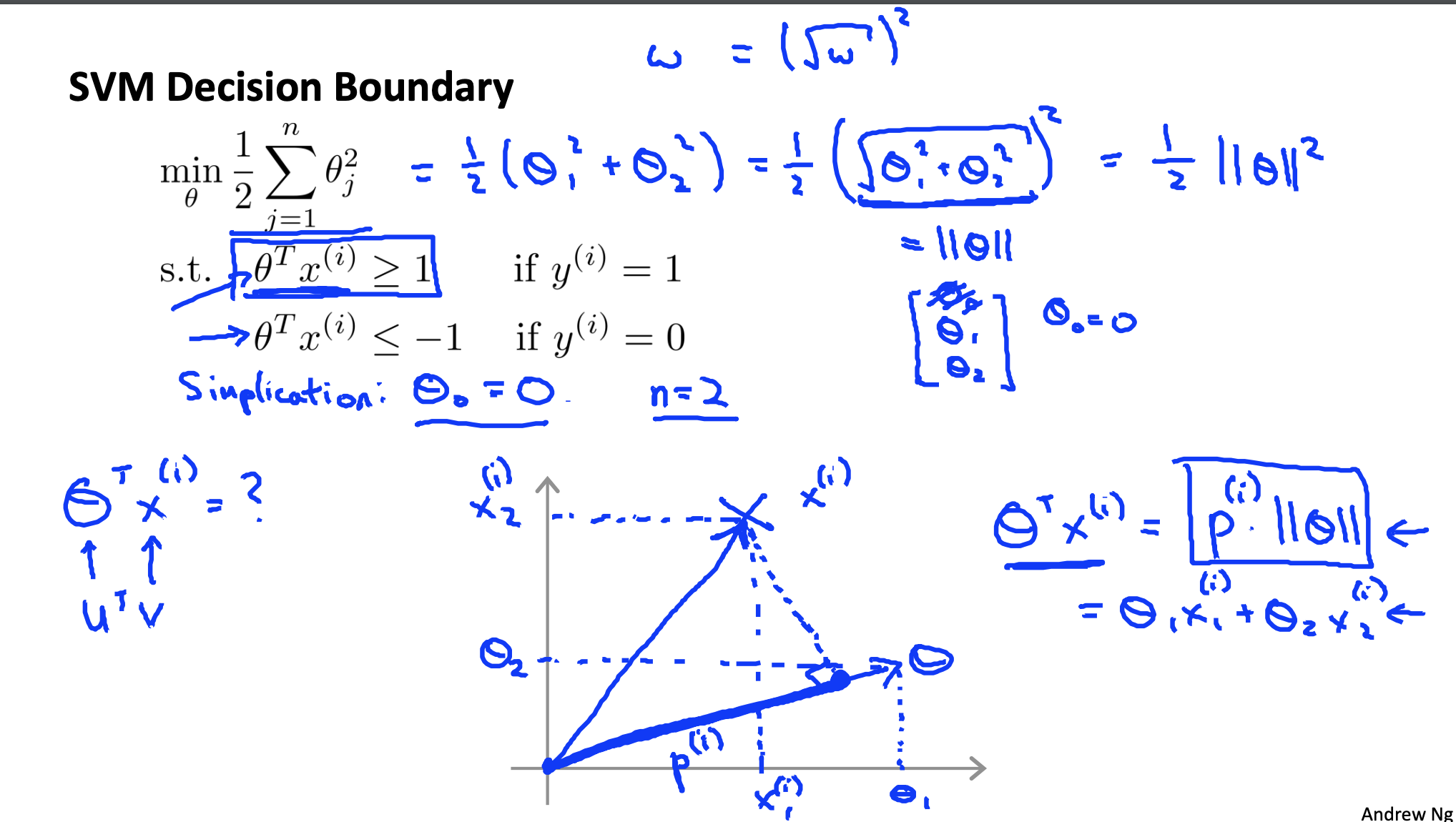
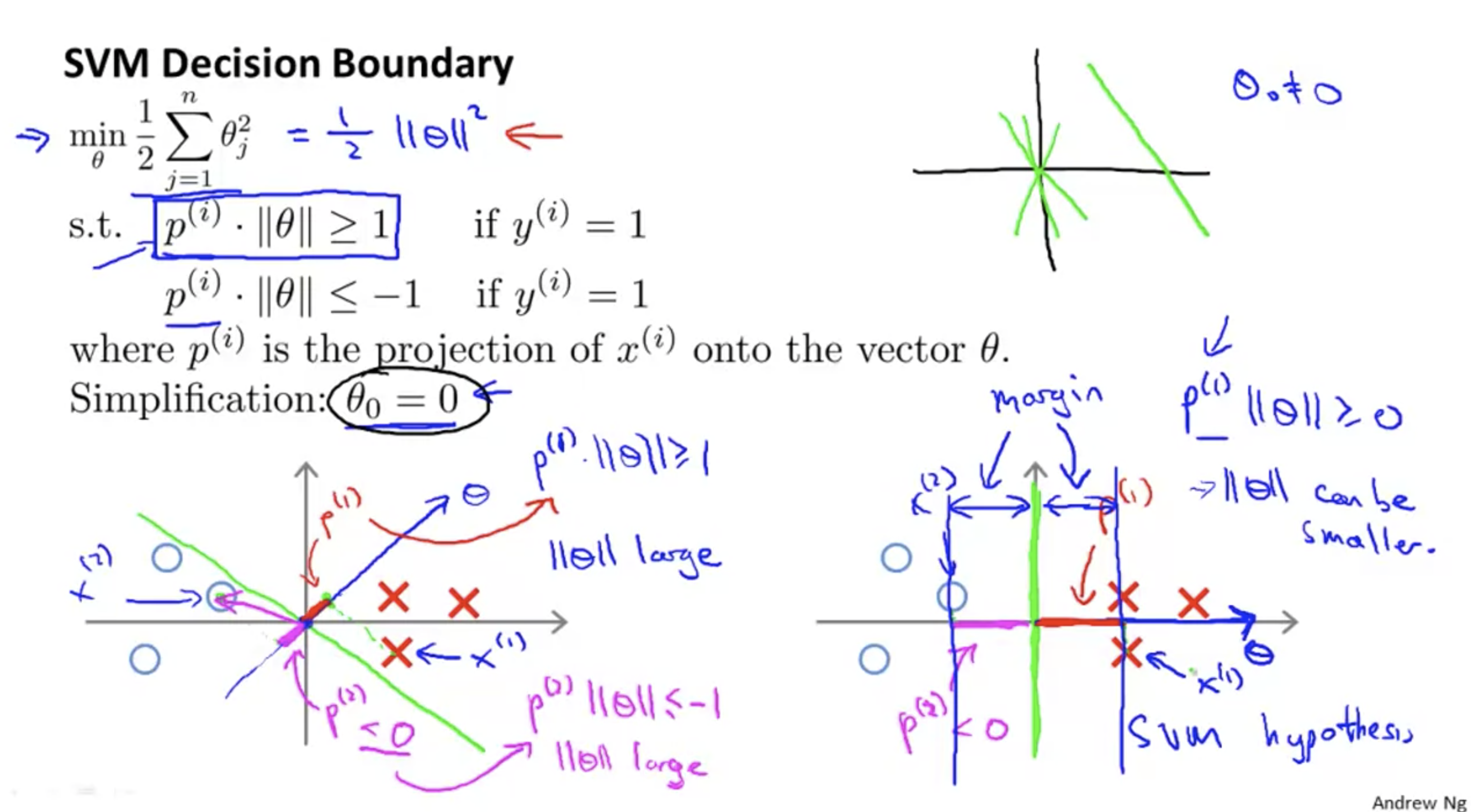
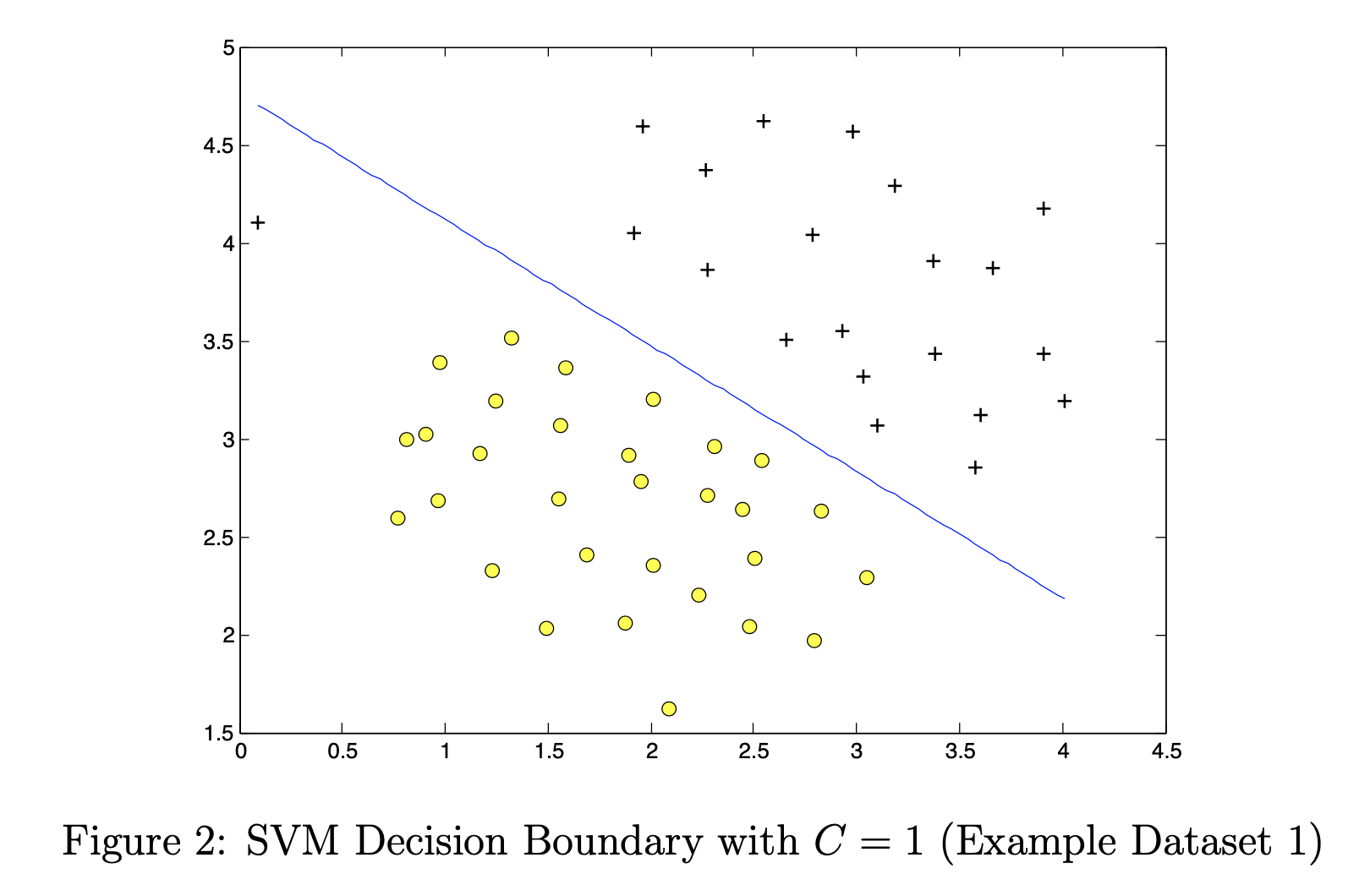
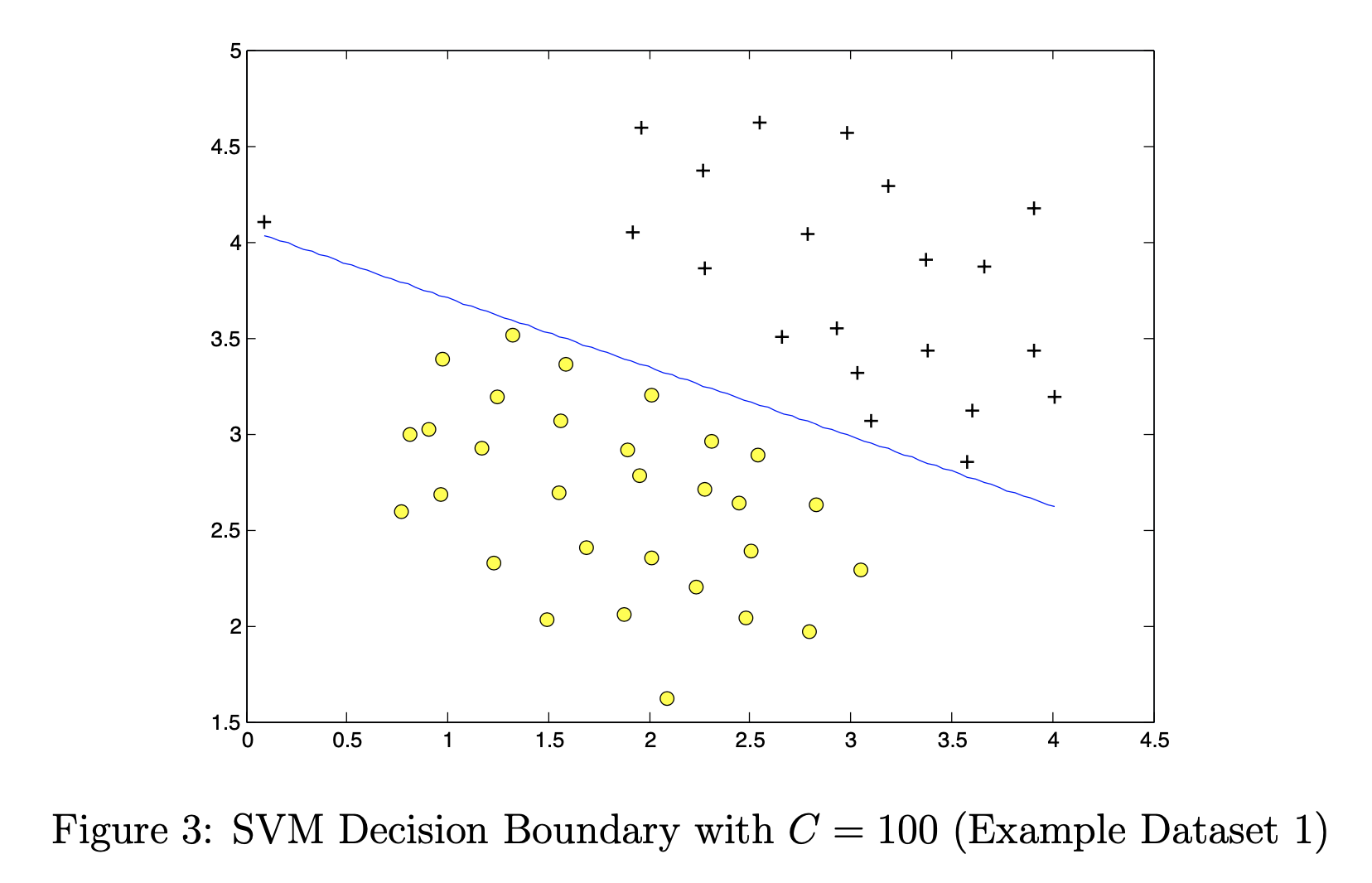
svm decision boundary,
Kernel (similarity) function
SVM is good at solving linear non separable classification problems.
Describe the similarity (distance) between a sample and the marked point. It is equivalent to mapping to a higher dimension.
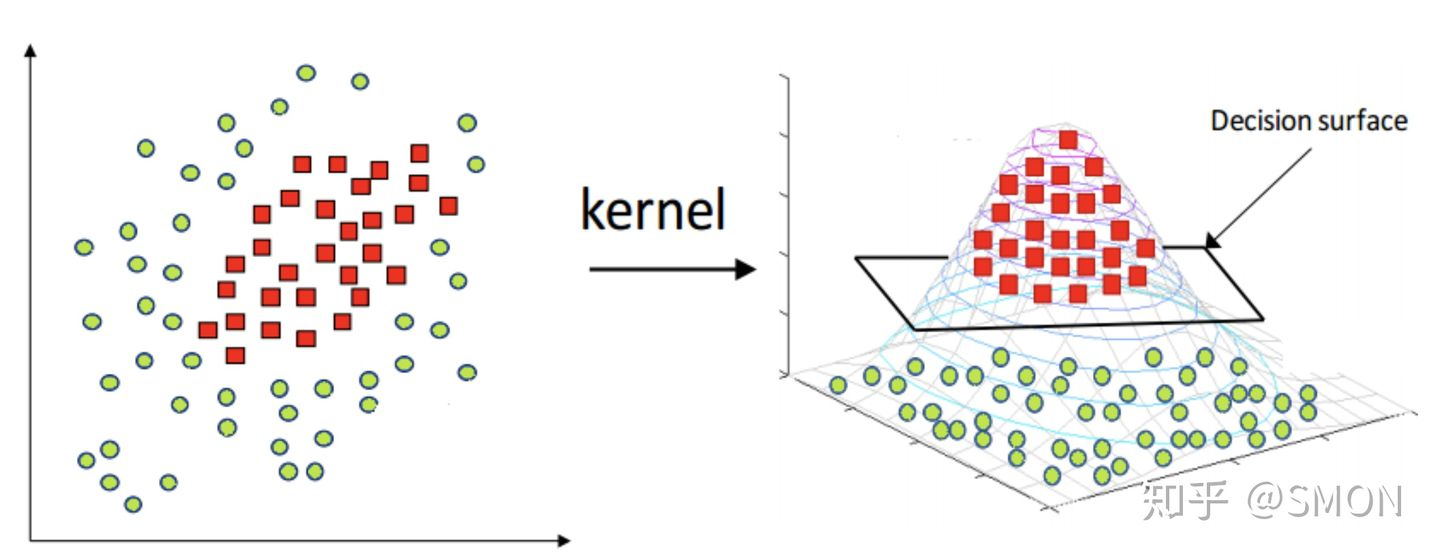
Gaussian kernel function
Gaussian kernel function is used to measure the distance between a pair of samples, such as the distance between (xi, xj).

The kernel function represents the distance between the sample point and the marked point (similarity):

σ It determines the decline speed of the similarity measurement function when the sample pair is far away from the edge.
σ The larger the slope, the smoother the slope and the slower the descent:
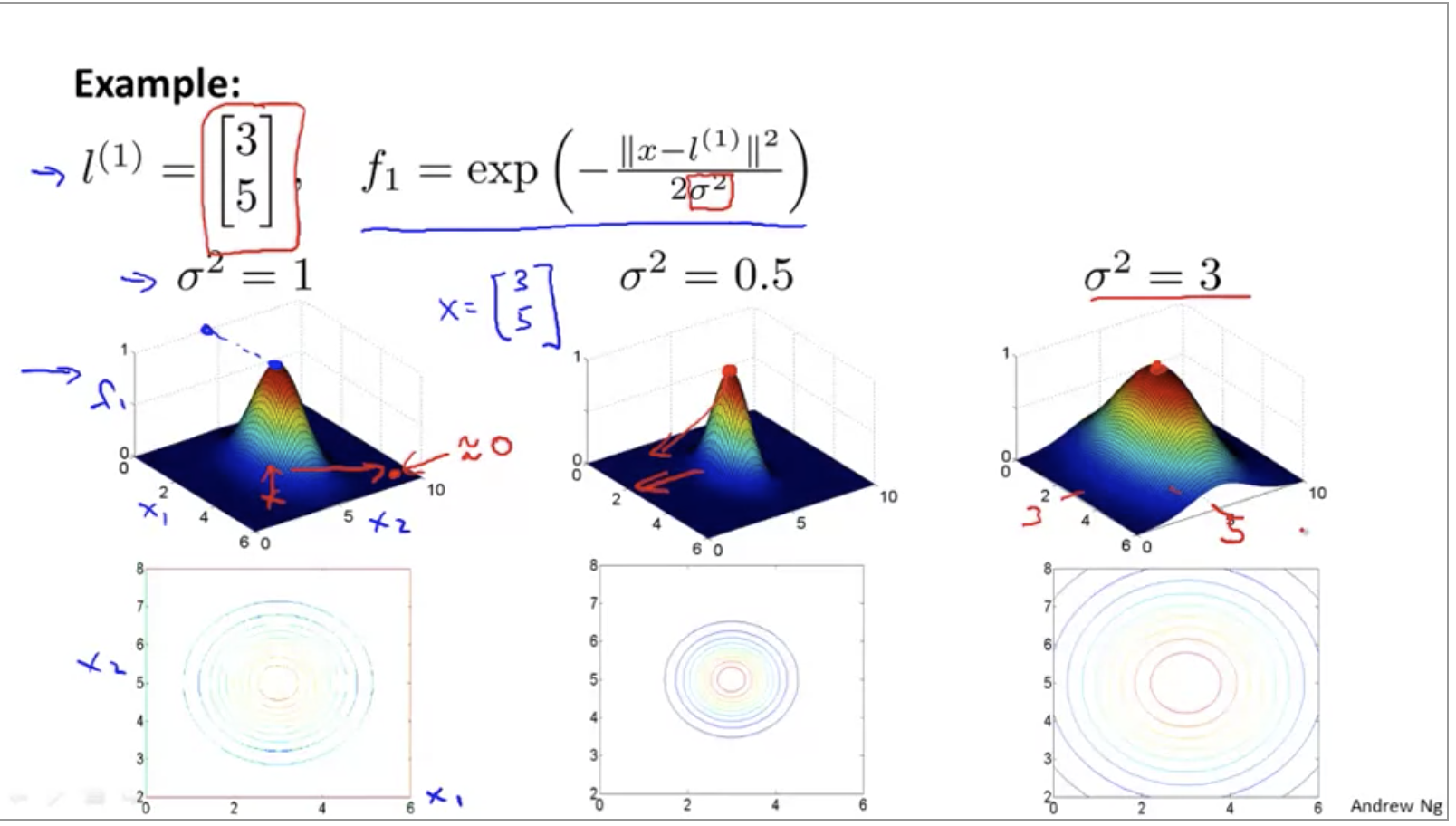
The closer to the marked point i, fi is approximately equal to 1, and the farther away it is, it is 0. In the figure below, the prediction 1 inside the red circle and the prediction 0 outside the red circle:

How to select a marker point? Treat all training set points as marker points:
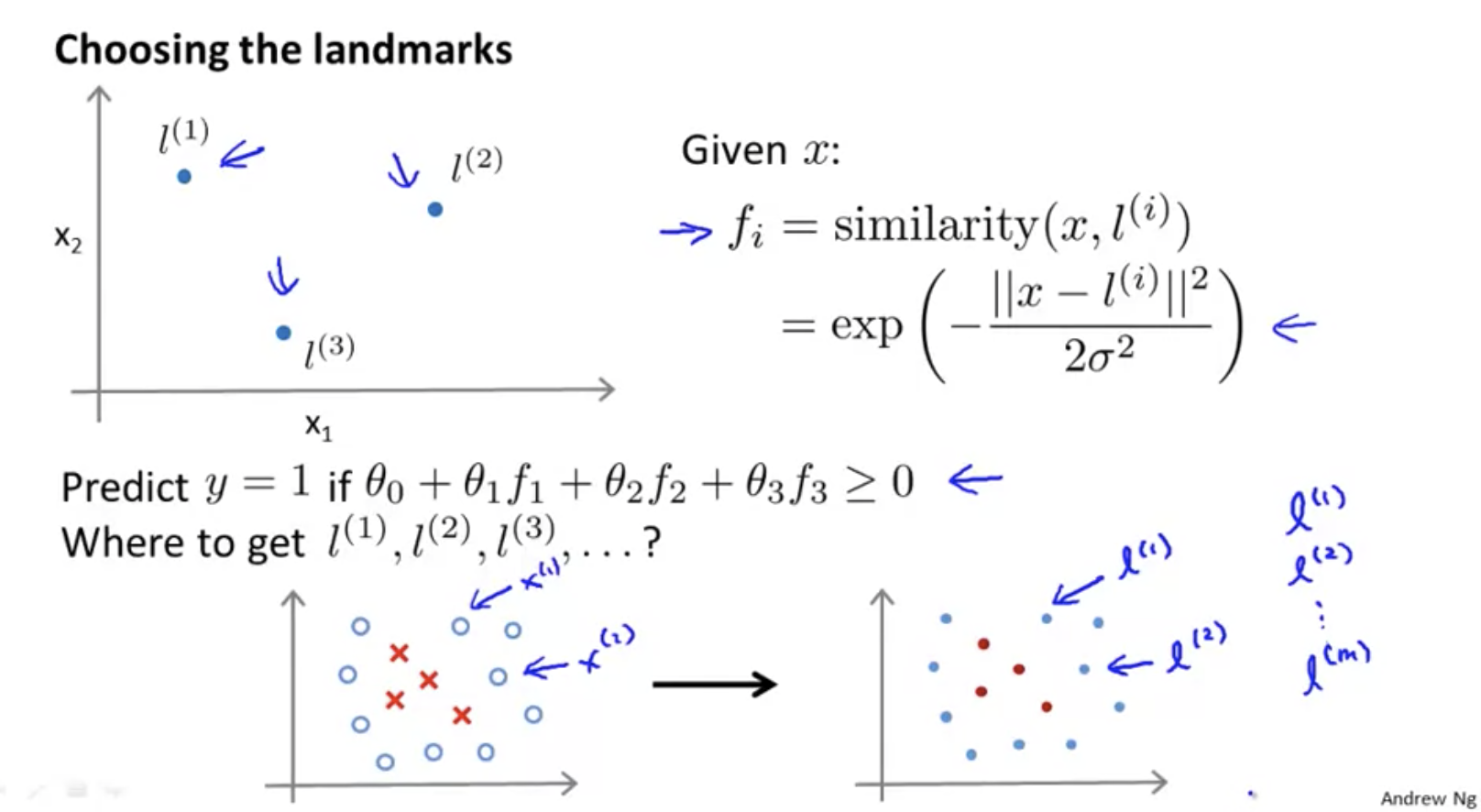
among


SVM parameters
C stands for punishment for misclassification. amount to λ The reciprocal of.
The larger the C, the smaller the deviation and the larger the variance;
The smaller the C, the greater the deviation and the smaller the variance;

Steps to use SVM
- Select parameter C
- Select kernel function
When there is no kernel function, it becomes a linear regression problem. It can also be considered that the linear kernel function is used at this time.
If Gaussian kernel function is selected, parameters need to be selected σ.


Note: do scaling first
Multi classification problem
- Many SVM packages already contain multi classification functions
- You can also use the one vs all method

Advantages and disadvantages of SVM
The advantages of support vector machine are:
- Because SVM is a convex optimization problem, the solution must be global optimization rather than local optimization.
- It is applicable not only to linear problems, but also to nonlinear problems (using kernel technique).
- SVM can also be used for data with high-dimensional sample space, because the complexity of the data set only depends on the support vector rather than the dimension of the data set, which avoids the "dimension disaster" in a sense.
- The theoretical basis is relatively perfect (for example, neural network is more like a black box).
The disadvantages of support vector machine are:
- The solution of quadratic programming problem will involve the calculation of m-order matrix (M is the number of samples), so SVM is not suitable for super large data sets. (SMO algorithm can alleviate this problem)
- It is only applicable to two classification problems. (the generalization of SVM SVR is also applicable to regression problems; multiple classification problems can be solved through the combination of multiple SVM)
SVM vs logistic regression vs neural network
How to choose the method?

task
gaussianKernel.m
function sim = gaussianKernel(x1, x2, sigma)
%RBFKERNEL returns a radial basis function kernel between x1 and x2
% sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
% and returns the value in sim
% Ensure that x1 and x2 are column vectors
x1 = x1(:); x2 = x2(:);
% You need to return the following variables correctly.
% sim = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the similarity between x1
% and x2 computed using a Gaussian kernel with bandwidth
% sigma
%
%
sim = exp(-sum((x1 - x2).^2)/(2*sigma^2));
% =============================================================
end
dataset3Params.m
Note two syntax here:
- python like for... in... Traversal list:
varList = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30];
for C = varList,
for sigma = varList,
...
- When a function is used as a parameter, the method of representing the parameter is as follows:
model = svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma));
dataset3Params.m:
function [C, sigma] = dataset3Params(X, y, Xval, yval)
%DATASET3PARAMS returns your choice of C and sigma for Part 3 of the exercise
%where you select the optimal (C, sigma) learning parameters to use for SVM
%with RBF kernel
% [C, sigma] = DATASET3PARAMS(X, y, Xval, yval) returns your choice of C and
% sigma. You should complete this function to return the optimal C and
% sigma based on a cross-validation set.
%
% You need to return the following variables correctly.
C = 1;
sigma = 0.3;
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the optimal C and sigma
% learning parameters found using the cross validation set.
% You can use svmPredict to predict the labels on the cross
% validation set. For example,
% predictions = svmPredict(model, Xval);
% will return the predictions on the cross validation set.
%
% Note: You can compute the prediction error using
% mean(double(predictions ~= yval))
%
varList = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30];
minError = inf;
minC = 1;
minSigma = 0.01;
for C = varList,
for sigma = varList,
model = svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma));
predictions = svmPredict(model, Xval);
error = mean(double(predictions ~= yval));
if error < minError,
minError = error;
minC = C;
minSigma = sigma;
end
end
end
C = minC;
sigma = minSigma;
% =========================================================================
end
processEmail.m
The following is an example of mail classification.
First, normalize the email text, such as replacing all links with httpaddr and money with dollar:
function word_indices = processEmail(email_contents)
%PROCESSEMAIL preprocesses a the body of an email and
%returns a list of word_indices
% word_indices = PROCESSEMAIL(email_contents) preprocesses
% the body of an email and returns a list of indices of the
% words contained in the email.
%
% Load Vocabulary
vocabList = getVocabList();
% Init return value
word_indices = [];
% ========================== Preprocess Email ===========================
% Find the Headers ( \n\n and remove )
% Uncomment the following lines if you are working with raw emails with the
% full headers
% hdrstart = strfind(email_contents, ([char(10) char(10)]));
% email_contents = email_contents(hdrstart(1):end);
% Lower case
email_contents = lower(email_contents);
% Strip all HTML
% Looks for any expression that starts with < and ends with > and replace
% and does not have any < or > in the tag it with a space
email_contents = regexprep(email_contents, '<[^<>]+>', ' ');
% Handle Numbers
% Look for one or more characters between 0-9
email_contents = regexprep(email_contents, '[0-9]+', 'number');
% Handle URLS
% Look for strings starting with http:// or https://
email_contents = regexprep(email_contents, ...
'(http|https)://[^\s]*', 'httpaddr');
% Handle Email Addresses
% Look for strings with @ in the middle
email_contents = regexprep(email_contents, '[^\s]+@[^\s]+', 'emailaddr');
% Handle $ sign
email_contents = regexprep(email_contents, '[$]+', 'dollar');
% ========================== Tokenize Email ===========================
% Output the email to screen as well
fprintf('\n==== Processed Email ====\n\n');
% Process file
l = 0;
while ~isempty(email_contents)
% Tokenize and also get rid of any punctuation
[str, email_contents] = ...
strtok(email_contents, ...
[' @$/#.-:&*+=[]?!(){},''">_<;%' char(10) char(13)]);
% Remove any non alphanumeric characters
str = regexprep(str, '[^a-zA-Z0-9]', '');
% Stem the word
% (the porterStemmer sometimes has issues, so we use a try catch block)
try str = porterStemmer(strtrim(str));
catch str = ''; continue;
end;
% Skip the word if it is too short
if length(str) < 1
continue;
end
% Look up the word in the dictionary and add to word_indices if
% found
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to add the index of str to
% word_indices if it is in the vocabulary. At this point
% of the code, you have a stemmed word from the email in
% the variable str. You should look up str in the
% vocabulary list (vocabList). If a match exists, you
% should add the index of the word to the word_indices
% vector. Concretely, if str = 'action', then you should
% look up the vocabulary list to find where in vocabList
% 'action' appears. For example, if vocabList{18} =
% 'action', then, you should add 18 to the word_indices
% vector (e.g., word_indices = [word_indices ; 18]; ).
%
% Note: vocabList{idx} returns a the word with index idx in the
% vocabulary list.
%
% Note: You can use strcmp(str1, str2) to compare two strings (str1 and
% str2). It will return 1 only if the two strings are equivalent.
%
for i = 1:length(vocabList),
if strcmp(str, vocabList(i))==1,
word_indices = [word_indices; i];
break;
end
end
% =============================================================
% Print to screen, ensuring that the output lines are not too long
if (l + length(str) + 1) > 78
fprintf('\n');
l = 0;
end
fprintf('%s ', str);
l = l + length(str) + 1;
end
% Print footer
fprintf('\n\n=========================\n');
end
emailFeatures.m
function x = emailFeatures(word_indices)
%EMAILFEATURES takes in a word_indices vector and produces a feature vector
%from the word indices
% x = EMAILFEATURES(word_indices) takes in a word_indices vector and
% produces a feature vector from the word indices.
% Total number of words in the dictionary
n = 1899;
% You need to return the following variables correctly.
x = zeros(n, 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return a feature vector for the
% given email (word_indices). To help make it easier to
% process the emails, we have have already pre-processed each
% email and converted each word in the email into an index in
% a fixed dictionary (of 1899 words). The variable
% word_indices contains the list of indices of the words
% which occur in one email.
%
% Concretely, if an email has the text:
%
% The quick brown fox jumped over the lazy dog.
%
% Then, the word_indices vector for this text might look
% like:
%
% 60 100 33 44 10 53 60 58 5
%
% where, we have mapped each word onto a number, for example:
%
% the -- 60
% quick -- 100
% ...
%
% (note: the above numbers are just an example and are not the
% actual mappings).
%
% Your task is take one such word_indices vector and construct
% a binary feature vector that indicates whether a particular
% word occurs in the email. That is, x(i) = 1 when word i
% is present in the email. Concretely, if the word 'the' (say,
% index 60) appears in the email, then x(60) = 1. The feature
% vector should look like:
%
% x = [ 0 0 0 0 1 0 0 0 ... 0 0 0 0 1 ... 0 0 0 1 0 ..];
%
%
for i = word_indices,
x(i) = 1;
end
% =========================================================================
end
In fact, only parameter selection and preprocessing are done in the whole process, and the principle of SVM is rarely involved.
Think of this picture:
