The original subproblem is divided into multiple subproblems, which do not need to be solved by recursive programming
Dynamic Programming (DP) requires transfer equations and boundary conditions.
catalogue
2, 198 raid homes and plunder houses
2.2.1 there are many judgment conditions
2.2.2 optimization (recommended)
I 70. Climb stairs
1.1 Title Description
Suppose you are climbing stairs. You need steps n to reach the roof.
You can climb one or two steps at a time. How many different ways can you climb to the roof?
Note: given n , is a positive integer.

1.2 code
Ideas and algorithms:
Use f(x) to represent the number of schemes for climbing to the x-th step. Consider that the last step may span one step or two steps.
1. Transfer equation of dynamic programming:
f(x) = f(x - 1) + f(x - 2)
2. Discuss the boundary conditions again: we start to climb from level 0, so we can see that there is only one scheme from level 0 to level 0, that is, f(0) = 1; There is only one scheme from level 0 to level 1, that is, climb one level, f(1) = 1. According to the transfer equation, f(2) = 2, f(3) = 3, f(4) = 5
public int climbStairs(int n){
int pre1=1,pre2=1;
for (int i = 1; i < n; i++) {
int temp=pre2
pre2=pre1+pre2;
pre1=temp;
}
return pre2;
}Complexity analysis:
Time complexity: the loop is executed n times and takes a constant time cost each time, so the progressive time complexity is O(n).
Space complexity: here only constant variables are used as auxiliary space, so the complexity of asymptotic space is O(1).
supplement
There are two other ways:
- With the increasing of N, O(n) may not meet our needs. We can use the method of "matrix fast power" to accelerate the algorithm to O(logn).
- We can also substitute n , into the calculation result of the general term formula of Fibonacci sequence, but if we use floating-point calculation to realize it, there may be accuracy error.
II 198. House raiding
2.1 Title Description
You are a professional thief who plans to steal houses along the street. There is a certain amount of cash hidden in each room. The only restrictive factor affecting your theft is that the adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.
Given a non negative integer array representing the amount stored in each house, calculate the maximum amount you can steal overnight without touching the alarm device.
2.2 code
2.2.1 there are many judgment conditions
If you have a room, steal this one f1=m1. If there are two rooms, the one with more stolen amount f2=max{m1,m2}. If there are three rooms, F3 = max {M1, m3}, {m2}, that is, f3=max{f1+m3, f2}.
If there are four rooms, if you steal the largest of the first two rooms plus the fourth, or the first three rooms, that is {f2+m4}or f3, so f4=max{{f2+m4}, f3}.
You can write the transfer equation:

public static int rob(int[] nums) {
if (nums.length==1) return nums[0];
if (nums.length==2) return Math.max(nums[0],nums[1]);
int cur=0;
int pre1=nums[0],pre2=Math.max(nums[0],nums[1]);
for (int i = 2; i < nums.length; i++) {
cur=Math.max(pre1+nums[i],pre2);
pre1=pre2;
pre2=cur;
}
return cur;
}Complexity analysis
Time complexity: O(n), where n is the length of the array. You only need to traverse the array once.
Space complexity: O(1). Using the rolling array, you can only store the maximum total amount of the first two houses without storing the results of the whole array, so the space complexity is O(1).
2.2.2 optimization (recommended)
public static int rob(int[] nums) {
if (nums.length==1) return nums[0];
int pre1=nums[0],pre2=Math.max(nums[0],nums[1]);
for (int i = 2; i < nums.length; i++) {
int temp=pre2;
pre2=Math.max(pre1+nums[i],pre2);
pre1=temp;
}
return pre2;
}
III 213. House raiding II
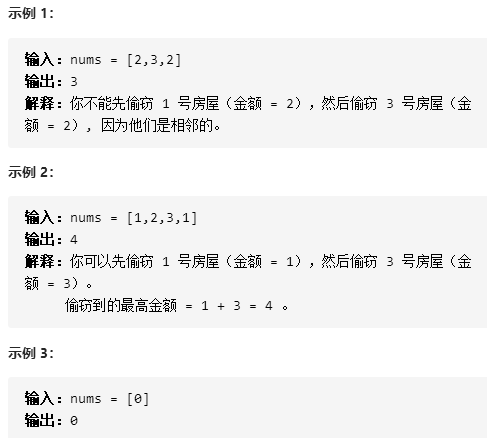
Title Description
You are a professional thief. You plan to steal houses along the street. There is a certain amount of cash in each room. All the houses in this place are in a circle, which means that the first house and the last house are next to each other. At the same time, adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.
Given a non negative integer array representing the amount stored in each house, calculate the maximum amount you can steal tonight without touching the alarm device.
3.2 code
Suppose the length of array nums is n. If the last house is not stolen, the subscript range of the stolen house is [0,n − 2]; If the first house is not stolen, the subscript range of the stolen house is [1,n − 1].
After determining the subscript range of the stolen house, you can solve it by the method of question 198.
public static int rob(int[] nums) {
int n=nums.length;
if (nums==null || n == 0) return 0;
if (n == 1) return nums[0];
if (n == 2) return Math.max(nums[0], nums[1]);
return Math.max(robRange(nums,0,n-2),robRange(nums,1,n-1));
}
public static int robRange(int[] nums,int start,int end){
int pre1 = nums[start], pre2 = Math.max(nums[start], nums[start+1]);
for (int i = start+2; i <= end; i++) {
int temp=pre2;
pre2 = Math.max(pre1 + nums[i], pre2);
pre1 = temp;
}
return pre2;
}