Machine learning watermelon book after class Exercise 3.4 -- python solution cross validation and the right rate regression error rate of leave one method
Watermelon book P69
3.3 select two UCI data sets and compare the error rate of pair rate regression estimated by 10 fold cross validation method and leave one method
Dataset: Iris dataset
Dataset attribute information:
1. Sepal length (in cm)
2. Sepal width (in cm)
3. Petal length (in cm)
4. Petal width (in cm)
5. Category:
Description of data set processing: there are three Iris species in this data set, namely iris setosa, iris versicolor and iris virginica. Since the title requires two methods to process the data set, we divide iris setosa and iris versicolor into one data set (called No. 1 data set), and use the leave one method to divide the data set, Iris versicolor and iris virginica are put into another data set (called data set 2) and divided using cross validation.
[Code]
#Iris setosa is marked as 0, iris versicolor is marked as 1, and iris virginica is marked as 2
def loadDataset(filename):
dataset_12=[]
dataset_23=[]
with open(filename,'r',encoding='utf-8') as csvfile:
csv_reader = csv.reader(csvfile)
for row in csv_reader:
if row[4] == 'Iris-setosa':
row[4]=0
dataset_12.append(copy.deepcopy(row))
elif row[4]=='Iris-virginica':
row[4]=2
dataset_23.append(copy.deepcopy(row) )
else:
row[4]=1
dataset_12.append(copy.deepcopy(row))
dataset_23.append(copy.deepcopy(row))
data_12 = [[float(x) for x in row] for row in dataset_12]
data_23= [[float(x) for x in row] for row in dataset_23]
# print(data_12)
# print(data_23)
return data_12,data_23
Note: in this program, we use append (copy. Deep copy (row)) for deep copy to avoid the operation of the array affecting the change of the original array, the same below!!!!
For dataset 2:
[code idea] we use the 10 fold cross validation method to divide the data set into training set and test set each time, then use the gradient descent method to train the training set, and use the test set to obtain the accuracy rate each time. Finally, we take the average of the accuracy rate of 10 times, that is, the final accuracy rate.
[detailed process]
-
Firstly, we use the functions in python to perform 10 fold cross validation division. Since the index of the divided data is returned, we need to find the corresponding data element, and then preprocess the data in the training set and test set (add a column of 1, 0, 1 to store the real mark at the end of the array), and then we can participate in the training, We set the number of iterations to 2000. We find that when the number of iterations reaches 2000, the accuracy is difficult to increase again. Therefore, we take 2000 as the termination condition, compare the obtained w with 10 test sets, get 10 groups of accuracy, and take the average value.
-
Finally, we get the accuracy rate of the 10 fold cross validation method is 96%!
#Define sigmoid function def sigmoid(z): return 1.0 / (1 + np.exp(-z)) #Calculation accuracy def testing(testset,w,testlabel): data = np.mat(testset).astype(float) y = sigmoid(np.dot(data, w)) b, c = np.shape(y) # The function is to view the dimension of matrix or array. rightcount = 0 for i in range(b): flag = -1 if y[i, 0] > 0.5: flag = 1 elif y[i, 0] < 0.5: flag = 0 if testlabel[i] == flag: rightcount += 1 rightrate = rightcount / len(testset) return rightrate #Iterative calculation of w def training(dataset,labelset,testset,testlabel): # np. Dot (a, b) dot multiplication of a and B matrices # np. Transfer() transpose # np.ones((m,n)) creates a multidimensional array of M rows and N columns data=np.mat(dataset).astype(float) label=np.mat(labelset).transpose() w = np.ones((len(dataset[0]),1)) #step n=0.0001 # Calculate the accuracy rate once per iteration (the accuracy rate on the test set) # When the accuracy of 0.90 is reached, stop the iteration rightrate=0.0 count=0 while count<5000: c=sigmoid(np.dot(data,w)) b=c-label change = np.dot(np.transpose(data),b) w=w-change*n #Forecast, update accuracy if rightrate<testing(testset,w,testlabel): rightrate=testing(testset,w,testlabel) count+=1 return rightrate def formdata(dataset,flag):#flag=1 represents data preprocessing for data set 1, and false = 2 is for data set 2 #It is mainly to standardize the training set and test set, so as to facilitate the accuracy calculation and iterative calculation of w in the next step data=[] label=[] if flag==1: for row in dataset: label.append(copy.deepcopy(row[4])) row[4]=1 data.append(copy.deepcopy(row)) elif flag == 2: for row in dataset: label.append(copy.deepcopy(row[4]-1)) row[4]=1 data.append(copy.deepcopy(row)) return data,label def changedata(dataset,train_index,test_index):#Process the data set and add the last column as 1 trainset=[] testset=[] for i in train_index: trainset.append(copy.deepcopy(dataset[i])) for i in test_index: testset.append(copy.deepcopy(dataset[i])) return trainset,testset #The data set 23 was classified by 10 fold cross validation def Flod_10(dataset): sam=KFold(n_splits=10) rightrate=0.0 for train_index,test_index in sam.split(dataset):#Get the indexes of training set and test set # Next, convert the index into the corresponding element, and iterate the training set to find the maximum accuracy each time trainset,testset=changedata(dataset,train_index,test_index) #print(trainset) trainset,trainlabel=formdata(trainset,2) testset,testlabel=formdata(testset,2) rightrate+=training(trainset,trainlabel,testset,testlabel) print(rightrate/10)Final result:
[[-1.90048431] [-1.20567294] [ 2.31544454] [ 2.66095658] [-0.20997301]] [[-1.86985439] [-1.3288315 ] [ 2.3427924 ] [ 2.64797632] [-0.16119412]] [[-1.90055107] [-1.29322442] [ 2.37973509] [ 2.68461371] [-0.26297932]] [[-2.00438577] [-1.18000688] [ 2.43352222] [ 2.65712983] [-0.15617894]] [[-1.94737348] [-1.16692044] [ 2.35919664] [ 2.59038908] [-0.14542583]] [[-1.91467144] [-1.22980709] [ 2.27891615] [ 2.74578832] [-0.23887025]] [[-1.94810073] [-1.27450893] [ 2.37093425] [ 2.64955955] [-0.24649082]] [[-1.99150258] [-1.25235181] [ 2.35312496] [ 2.75221192] [-0.20701229]] [[-1.96302072] [-1.29024687] [ 2.31087635] [ 2.8008307 ] [-0.16047752]] [[-1.9630222 ] [-1.35486554] [ 2.50563773] [ 2.44772595] [-0.25646535]] 0.96
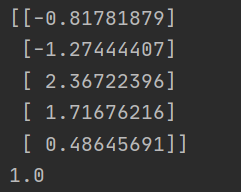
For dataset 1
[code idea] we use the leave one method to divide. 75% of the data set is used as the training set and 25% as the test set. Since the number of iris setosa and iris versicolor is 1:1, we use the stratified sampling method. We take 75% of each flower as the training set and 25% as the test set, and then iterate to find the accuracy!
#Set aside method - classify data set 12
#75% of the samples were used for training and the rest for testing
def LeftOut(dataset):
train12=[]
test12=[]
for i in range(len(dataset)):
if i<=37:
train12.append(copy.deepcopy(dataset[i]))
elif i>50 and i<=88:
train12.append(copy.deepcopy(dataset[i]))
else:
test12.append(copy.deepcopy(dataset[i]))
trainset,trainlabel=formdata(train12,1)
testset,testlabel=formdata(test12,1)
rightrate=training(trainset,trainlabel,testset,testlabel)
print(rightrate)
final result