1, Early termination of a loop with a break statement

Function: make the process jump outside the loop body, and then execute the statements below the loop body.

Note: the break statement can only be used in loop statements and switch statements, not alone.

Charity fundraising will be held among 1000 students in the Department. It will end when the total amount reaches 100000 yuan. The number of donations and the average number of donations per person at this time will be counted.

#include <stdio.h>
#define SUM 100000 	// Specifies that the symbolic constant sum represents 100000
int main()
{
	float amount,aver,total; 
	int i;
	for (i=1,total=0;i<=1000;i++)
	{
		printf("please enter amount:");
		scanf("%f",&amount);
		total=total+amount; 
		if(total>=SUM) break; 
	}
	aver=total/i;
	printf("num=%d\naver=%10.2f\n",i,aver); 
	return 0;
}

2, Terminate the loop early with the continue statement

Function: end this cycle, that is, skip the following unexecuted statements in the cycle body, go to the end point of the cycle body, then execute "expression 3" in the for statement, and then determine whether to execute the cycle next time.

It is required to output a number between 100 and 200 that cannot be divided by 3.

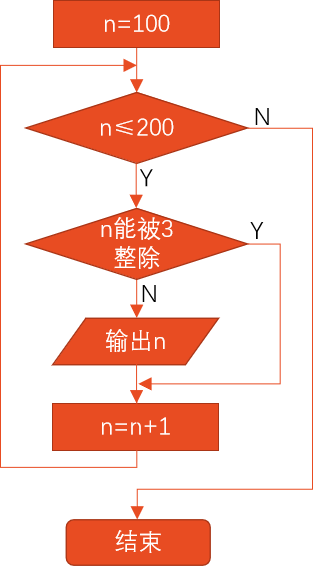
#include <stdio.h>
int main()
{	int n;
	for (n=100;n<=200;n++)
	{	if (n%3==0)
			continue;
		printf("%d ",n);
	}
	printf("\n");
	return 0;
}

3, The difference between break statement and continue statement

Output the following 4 × 5 matrix

#include <stdio.h>
int main()
{
	int i,j,n=0;
	for(i=1;i<=4;i++)
		for(j=1;j<=5;j++,n++)		//n is used to accumulate the number of output data
		{	if(n%5==0) printf("\n");	//Control line wrapping after outputting 5 data
		    //Empty statement; 	   Normal output
			//if (i==3 && j==1) break;  // The third line is missing
		    //if (i==3 && j==1) continue;// The first number of the third line is missing
			printf("%d\t",i*j);
		}  
	printf("\n");    
	return 0;
}

4, Example of cyclic procedure

1. Use the formula π / 4 ≈ 1 − 1 / 3 + 1 / 5 − 1 / 7 +... To find the approximate value of π until it is found that the absolute value of a certain item is less than 10-6 (this item is not accumulated).

Problem solving ideas: find rules:
(1) The molecule of each term is 1.
(2) The denominator of the latter term is the denominator of the previous term plus 2.
(3) The symbol of item 1 is positive. From item 2, the symbol of each item is opposite to that of the previous item.
After each item is calculated, check whether its absolute value is greater than or equal to 10-6.

#include <stdio.h>
#include <math.h> 				// The mathematical function fabs used in the program should include the header file math h
int main()
{	int sign=1;					//A sign used to represent a numeric value
	double pi=0.0,n=1.0,term=1.0;	//pi starts with the value of the polynomial, ends with the value of π, n represents the denominator, and term represents the value of the current term
	while(fabs(term)>=1e-6)		//Check whether the absolute value of the current term is greater than or equal to 10-6
	{	pi=pi+term;				//Add the current term to pi
		n=n+2;					//n+2 is the denominator of the next term 
		sign=-sign;				//sign stands for symbol, and the symbol of the next item is opposite to that of the previous item
		term=sign/n;				//Find the value term of the next item
	}
	pi=pi*4;						//The sum pi of polynomials multiplied by 4 is the approximate value of π
	printf("pi=%10.8f\n",pi);			//Approximate value of output π  
	return 0;
}

2. Find the first 40 numbers of Fibonacci series. This sequence has the following characteristics: the first and second numbers are 1 and 1. Starting from the third number, this number is the sum of the first two numbers. That is, the number sequence is 1,1,2,3,5,8,13,..., which is mathematically expressed as:
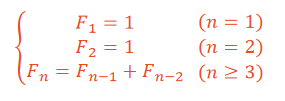This is an interesting classical mathematical problem: there is a pair of rabbits. They give birth to a pair of rabbits every month from the third month after birth. After the little rabbit grows to the third month, it gives birth to a pair of rabbits every month. Assuming that all rabbits do not die, what is the total number of rabbits per month?

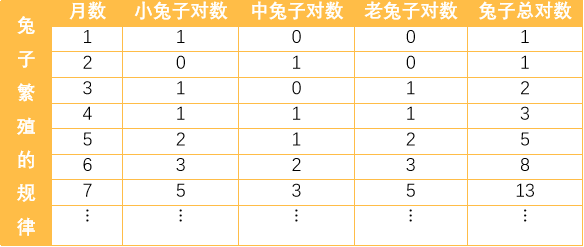
Note: it is assumed that the rabbits less than 1 month are small rabbits, those less than 1 month but less than 2 months are medium rabbits, and those more than 2 months are old rabbits.
Find the first 40 numbers of Fibonacci sequence.

#include <stdio.h>
int main()
{ 
	int f1=1,f2=1,f3;
	int i;
	printf("%12d\n%12d\n",f1,f2);
	for(i=1; i<=38; i++)
	{
		f3=f1+f2;
		printf("%12d\n",f3);
		f1=f2;
		f2=f3;
	}
	return 0;
}

3. Enter an integer n greater than 3 to determine whether it is prime.

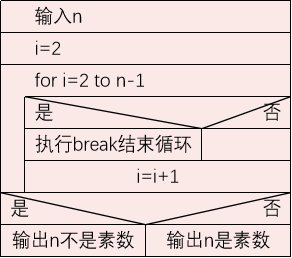
Method 1

#include <stdio.h>
int main()
{	int n,i;
	printf("please enter a integer number,n=?");
	scanf("%d",&n);
	for (i=2;i<n;i++)
		if(n%i==0) break;
	if(i<n) printf("%d is not a prime number.\n",n);
	else printf("%d is a prime number.\n",n);
	return 0;
}

Method 2
Program improvement:
In fact, n does not have to be removed by integers in the range of 2 ~ (n-1), but only by integers between 2 ~ √ n. Because each pair of factors of N must have one less than √ N and the other greater than √ n.

#include <stdio.h>
#include <math.h>
int main()
{	int n,i,k;
	printf("please enter a integer number,n=?");
	scanf("%d",&n);
	k=sqrt(n);
	for (i=2;i<=k;i++)
		if(n%i==0) break;
	if(i<=k) printf("%d is not a prime number.\n",n);
	else printf("%d is a prime number.\n",n);
	return 0;
}

4. Find all prime numbers between 100 and 200.

#include<stdio.h>
#include<math.h>
int main()
{	int n,k,i,m=0;
	for(n=101;n<=200;n=n+2)		//N changes from 100 to 200, and each odd number n is determined
	{	k=sqrt(n);
		for(i=2;i<=k;i++)
		if(n%i==0) break;			//If n is divided by i, the inner loop is terminated, and i < K + 1
		if(i>=k+1)				//If I > = K + 1, it means that n has not been divided
		{	printf("%d ",n);			//It should be determined that n is a prime number
			m=m+1;				//It is used to control a prime line within 10 m
		}
		if(m%10==0) printf("\n");	 //m accumulated to a multiple of 10, line feed
	}
	printf ("\n");
	return 0;
}

5. Translate the password. In order to keep the message confidential, it is often converted into a password according to a certain law, and then the receiver translates it back to the original text according to the agreed law. For example, a message can be changed into a password according to the following rules: the letter a becomes the letter E, a becomes e, that is, it becomes the fourth letter after it, W becomes a, X becomes B, Y becomes C, and Z becomes D.

Problem solving ideas:
(1) Determine which characters do not need to be changed and which characters need to be changed.
(2) Change the ASCII value of character c to the specified letter‘ A 'V' or 'a' V ': c=c+4‘ W 'Z' or 'W' Z ': c=c-22.

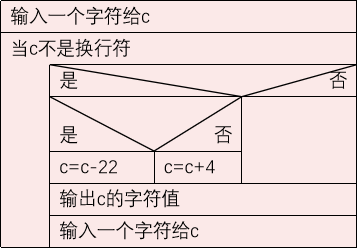
Method 1

#include <stdio.h>
int main()
{	char c;
	c=getchar();				//Enter a character into the character variable c
	while(c!='\n')				//Check whether the value of c is a newline '\ n'  
	{	if((c>='a' && c<='z') || (c>='A' && c<='Z'))	//c if letter
		{	if(c>='W' && c<='Z' || c>='w' && c<='z') c=c-22;
			//If it is one of the last four of the 26 letters, make c-22
			else c=c+4;		//If it is one of the first 22 letters, add 4 to c to become the fourth letter after it
		}
		printf("%c",c);			//Output changed characters
		c=getchar(); 			//Then enter the next character to the character variable c
	}
	printf("\n");
	return 0;
}

Method 2

#include <stdio.h>
int main()
{	char c;
				
	while((c=getchar())!='\n')				//Check whether the value of c is a newline '\ n'  
	{	if((c>='a' && c<='z') || (c>='A' && c<='Z'))	//c if letter
		{	 c=c+4;		

		}
		printf("%c",c);			//Output changed characters
		if(c>'Z' && c<='Z'+4 || c>'z' && c<='z'+4)  c=c-26;
			
	}
	printf("\n");
	return 0;
}