Data structure and algorithm
1. Overview of data structure and algorithm
1.1 general
Data structure is a subject that studies the way of organizing data. With programming language, there will be data structure Learning data structure well can write more beautiful and efficient code.
Program = data structure + algorithm
Data structure is the basis of algorithm. If you want to learn algorithm well, you need to learn data structure in place.
1.2 classification
The data structure includes linear structure and nonlinear structure
- linear structure
- There is a one-to-one linear relationship between data elements
- There are two different storage structures: sequential storage structure and chain storage structure.
-
- A linear table with sequential storage is called a sequential table, and the storage elements in the sequential table are continuous
- A linear list with linked storage is called a linked list. The storage elements in the linked list are not necessarily continuous. The address information of data elements and adjacent elements are stored in the element node
- Common linear structures are: array, queue, linked list and stack
- Nonlinear structure
- Typical nonlinear structures include multidimensional array, tree structure and graph structure
2. Sparse arrays and queues
2.1 sparse array
2.1.1 concept
Sparse array: when most element values in an array are the same and only a few values are different, when saving the array, full saving may occupy a lot of space, and too many repeated numbers are meaningless. Therefore, sparse array will be used to save the data.
2.1.2 application scenarios
In practice, for a chess game, the chess board simulation is often represented by a two-dimensional array. The value of 0 in the array represents the chess board, 1 represents the position of sunspots, and 2 represents the position of sunspots. When saving, exiting and connecting the chess board, it is necessary to save the chess board data.
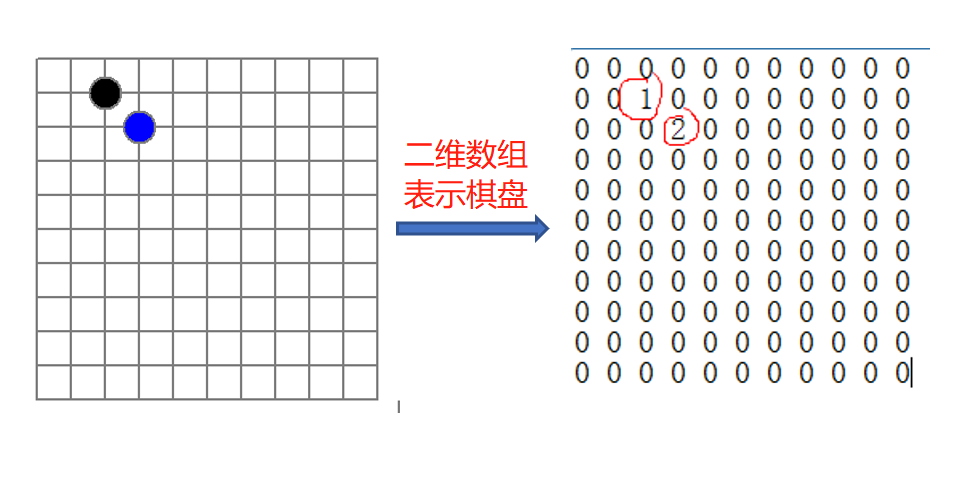
As shown in the above figure, when saving, many values of the chessboard represented by the two-dimensional array are the default value of 0. Saving in this way will record a lot of meaningless data.
2.1.3 sparse array resolution
In the above problem, when most of the elements in the array are 0 or an array with the same value, and only a few values are different, you can use a sparse array to save the array.
The processing method of sparse array is:
1) How many rows and columns are there in the record array? How many different values are there
2) The rows, columns and values of elements with different values are recorded in a small-scale array, so as to reduce the size of the program
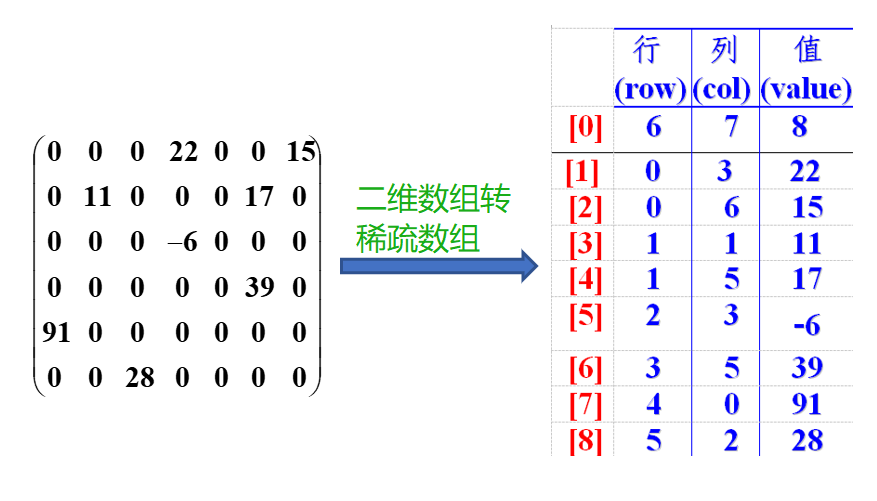
The process of converting ordinary two-dimensional array to sparse array:
-
row in sparse array: number of different values in two-dimensional array + 1;
-
Number of columns in sparse array column: 3 columns
The elements in the array represent:
-
The first row of data: the number of rows of the two-dimensional array, the number of columns of the two-dimensional array, and the number of different values in the two-dimensional array
-
The second row of data: rows with different values, columns with different values, and values with different values
-
...
The conversion of the above two-dimensional array is as follows:
2.1.4 code implementation
package com.kevin.sparsearray;
/**
* @author : kevin ding
* @date : 2022/2/9 13:42
* @description : Conversion of matrix and sparse matrix storage of two-dimensional data matrix of chessboard -- > first convert the ordinary two-dimensional array into a sparse array
* In the chessboard, 0 stands for chess space, 1 for sunspots, 2 for whites = = = = = = > many zeros will appear in the two-dimensional array, which is meaningless when stored. Sparse array is used
* Sparse array: there are three columns in the array. The three columns in the first row record the number of rows and columns of the original array, and the number of non-zero
* The number of lines cut down records the position and value of non-zero elements respectively
*/
public class SparseArray {
public static void main(String[] args) {
// 1. First create an original two-dimensional array
int[][] array = new int[10][10];
array[2][3] = 1;
array[3][4] = 2;
array[3][3] = 1;
array[1][3] = 2;
SparseArray demo = new SparseArray();
// 2. Print out the original array:
System.out.println("The original array is:");
demo.printArray(array);
// 3. Convert array to sparse array
int[][] sparseArray = demo.arrayTransToSparse(array);
// 4. Print sparse array
System.out.println("After converting to sparse array:");
demo.printArray(sparseArray);
// 5. Restore sparse matrix
int[][] normalArray = demo.sparseTransToNormalArray(sparseArray);
// 6. Output the restored matrix
demo.printArray(normalArray);
}
/**
* The process of converting an original array to a sparse array:
* 1.Traverse the entire original array and record the number of all non-zero elements
* 2.Create a sparse array according to the number of elements that are not zero: SparseArray array, array = New Int [sum + 1] [3];
* 3.Store the positions of non-zero elements in the corresponding sparse array respectively
*/
public int[][] arrayTransToSparse(int[][] array){
// 1. Traverse the whole original array and record the number of elements that are not zero
int count = 0;
for(int[] rows : array){
for(int data : rows){
if(data != 0){
count++ ;
}
}
}
// 2. Get the number of non-zero elements and create a sparse array:
int[][] sparseArray = new int[count+1][3];
sparseArray[0][0] = array.length;
sparseArray[0][1] = array[0].length;
sparseArray[0][2] = count;
// 3. Store non-zero elements in the corresponding location
int tempCount = 0; // The record is currently the number of elements that are not 0
for(int i = 0; i < array.length; i++){
for(int j = 0; j < array[i].length; j++){
if(array[i][j] != 0){
tempCount ++;
sparseArray[tempCount][0] = i;
sparseArray[tempCount][1] = j;
sparseArray[tempCount][2] = array[i][j];
}
}
}
return sparseArray;
}
// Traversal array
public void printArray(int[][] arr){
for(int[] rows: arr){
for (int data: rows){
System.out.print(data + "\t" );
}
System.out.println();
}
}
/**
* Convert sparse array to original array:
* 1. The original array is created according to the values of the first row, the first column, the first row and the second column of the sparse array
* 2. Fill the non-zero numbers in the remaining rows and columns
*/
public int[][] sparseTransToNormalArray(int[][] array){
// First, judge whether the sparse matrix has a value
if(array == null){
throw new RuntimeException("Sparse array is empty");
}
int[][] normalArray = new int[array[0][0]][array[0][1]];
// Starting from the second row, traverse each row of the sparse array
for(int i= 1; i<array.length; i++){
int rowIndex = array[i][0];
int columnIndex = array[i][1];
normalArray[rowIndex][columnIndex] = array[i][2];
}
return normalArray;
}
}
2.2 queue
2.2.1 introduction
- Queue is a sequential list, which can be realized by array or linked list;
- The queue follows the principle of * * first in first out (FIFO) * *. That is, the data stored in the queue first should be taken out first, and the data stored later should be taken out later;
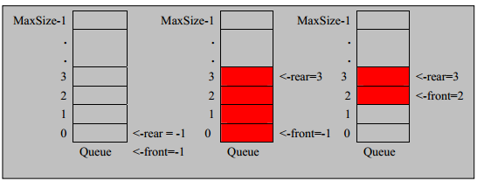
- The schematic diagram of the queue is as follows:
2.2.2 array simulation queue
- initialization:
- The queue structure should be declared as [maxfront] and the queue structure should be [maxfront] to point to the first and last of the simulated queue, and the array should point to [maxfront]; Initialize the tail of the team and the capital of the team to point to - 1;
- Method of simulating queue
-
Empty judgment: whether the queue is empty: rear == front
-
Queue full: whether the queue is full: rear == maxSize-1;
-
Join the queue (add data): addQueue:
- First judge whether the queue is full. If it is full, data cannot be added.
- Queue is not full, rear+=1; array[rear] = value;
-
Dequeue (fetch data): getQueue
- First judge whether the queue is empty. If it is empty, no element is out of the queue;
- The queue has a value, front+=1; return array[front];
-
Traversal (show all data):
- First judge whether the queue is empty
- Start from the front position of the queue to the rear, and then traverse
2.2.3 code implementation
- Array simulation queue
package com.kevin.arrayqueue;
/**
* @author : kevin ding
* @date : 2022/2/9 11:29
* @description : Create a queue class queue
* A pair of columns is an ordered list, which can be realized by array or linked list; The principle of first in, first out shall be followed for the column: the data of the column shall be stored first and taken out first
*/
public class Queue {
// The class of the column needs to have the maximum capacity of the attribute, including the head of the queue and the tail of the queue
private int maxSize;
private int front;
private int rear;
// Array simulation column
private int[] arr;
// Construction method of queue
public Queue( int maxSize){
this.maxSize = maxSize;
this.arr = new int[this.maxSize];
// The initial of the head and tail of the team point to - 1
this.front = -1;
this.rear = -1;
}
public boolean isFull(){
// When the end of the queue points to the last index, the queue is full
return this.rear == this.maxSize - 1;
}
public boolean isEmpty(){
// When the queue head and tail values are equal, the queue is empty
return this.rear == this.front;
}
public void addDataToQueue(int num){
// Adding elements first determines whether the queue is full
if(isFull()){
System.out.println("The queue is full and cannot be added...");
return;
}
// When not full, directly point the tail of the team to + 1
this.rear += 1;
arr[this.rear] = num;
}
public int getDataFromQueue(){
// First, judge whether the queue is empty
if(isEmpty()){
throw new RuntimeException("The queue is empty and cannot be taken");
}
//Team leader + 1 revaluation
this.front += 1;
return arr[this.front];
}
public void showQueue(){
// Air judgment
if(isEmpty()){
System.out.println("If the queue is empty, wool will be displayed..");
return;
}
// It needs to be displayed from the front of the queue to the end of the queue
for(int index = front+1; index <= rear; index++){
System.out.print(this.arr[index] + "\t");
}
System.out.println();
}
public int showFront(){
// Empty before displaying the header element
if(isEmpty()){
throw new RuntimeException("The queue is empty and there is no leader");
}
return arr[this.front+1];
}
}
- Console verification
package com.kevin.arrayqueue;
import java.util.Scanner;
/**
* @author : kevin ding
* @date : 2022/2/9 11:26
* @description : Queue validation using arrays
*/
public class ArrayQueueDemo {
public static void main(String[] args) {
// 1. Create a Queue through the Queue class
Queue queue = new Queue(4);
// 2. Write an interface to verify the queue function
boolean loop = true;
char choose = ' ';
Scanner sc = new Scanner(System.in);
while(loop){
System.out.println("a(add): Add data to queue");
System.out.println("g(get): Get data from queue");
System.out.println("h(head): Show team leader elements");
System.out.println("s(show): Show all queue elements");
System.out.println("e(exit): sign out");
System.out.println("Please enter the functions you need to complete:");
// Receive an input from the console
choose = sc.next().charAt(0);
// Judge choose operation
switch (choose){
case 'a':
System.out.println("Please enter the data to insert:");
int num = sc.nextInt();
queue.addDataToQueue(num);
System.out.println();
break;
case 'g':
try{
int data = queue.getDataFromQueue();
System.out.println("The extracted data is:" + data);
}catch (Exception ex){
System.out.println(ex.getMessage());
}
System.out.println();
break;
case 'h':
try {
int frontData = queue.showFront();
System.out.println("The header of the queue is:" + frontData);
}catch (Exception ex){
ex.printStackTrace();
}
System.out.println();
break;
case 's':
queue.showQueue();
System.out.println();
break;
case 'e':
loop = false;
System.out.println();
break;
default:
break;
}
}
sc.close();
System.out.println("Program exit....");
}
}
2.3 ring queue
In the verification of the above code, it is found that the queue simulated by the array can only be used once. Once the number of added data reaches maxSize, even if all the data is out of the queue, no more elements can be added. It is a one-time queue. The following uses an array to simulate a ring queue. Whenever there are elements out of the queue, new elements can be put on the stack to improve reusability.
2.3.1 train of thought analysis:
- For the ring queue, the mode is adopted to realize
- The variable meaning of front: front points to the first element of the queue, that is, it is initialized to 0, and array[front] is the first element of the queue;
- The variable meaning of rear: rear points to the last element of the queue, that is, to make a space available in the array as a convention. The initial value of rear is also 0;
- Conditions for queue full: (rear + 1)% maxsize = = front;
- Conditions for empty queue: rear == front;
- Number of valid data: (rear + maxsize - front)% maxsize
2.3.2 code implementation
- Cyclic queue code
package com.kevin.circlequeueDemo;
/**
* @author : kevin ding
* @date : 2022/2/10 0:12
* @description : Create a class of circular queue
*/
public class CircleQueue {
// The class of the column needs to have the maximum capacity of the attribute, including the head of the queue and the tail of the queue
private int maxSize;
private int front;
private int rear;
// Array simulation column
private int[] arr;
// Construction method of queue
public CircleQueue( int maxSize){
this.maxSize = maxSize;
this.arr = new int[this.maxSize];
// The team head points to 0, which directly indicates the current team head element
this.front = 0;
// The initial value of the tail of the queue is also 0, and the tail of the queue points to the last bit of the last element. Among them, an empty position is reserved in the agreed array, and no data is stored. Make an agreement
this.rear = 0;
}
public boolean isFull(){
// When reserving an empty space as an agreement, the judgment of whether it is full changes: (rear + 1)% maxSize == front indicates full
return (this.rear + 1) % this.maxSize == front;
}
public boolean isEmpty(){
// When the values of queue head and tail are equal, the judgment that the queue is empty does not change
return this.rear == this.front;
}
public void addDataToQueue(int num){
// Adding elements first determines whether the queue is full
if(isFull()){
System.out.println("The queue is full and cannot be added...");
return;
}
// When it is not full, directly add an element to the tail of the team. After adding, the tail of the team will move one bit later (it may cross the boundary and need to take a mold)
arr[this.rear] = num;
this.rear = (this.rear + 1) % this.maxSize;
}
public int getDataFromQueue(){
// First, judge whether the queue is empty
if(isEmpty()){
throw new RuntimeException("The queue is empty and cannot be taken");
}
//Because you need to return the value, you need to define a variable to store the value. After taking out the value of the head of the queue, you need to move the front first and then one bit to return the value
// When moving backward, we also need to consider the problem of array out of bounds and take modulus
int currentVal = arr[this.front];
this.front = (this.front + 1) % this.maxSize;
return currentVal;
}
public int totalNum(){
// The total number of elements in the queue is: (rear + maxsize - front)% maxsize
return (this.rear + this.maxSize - this.front) % this.maxSize;
}
public void showQueue(){
// Air judgment
if(isEmpty()){
System.out.println("If the queue is empty, wool will be displayed..");
return;
}
// Start from the front of the queue and display the number of traverses (index < front + total) (the total number of elements in the queue)
for(int index = front; index < front + totalNum(); index++){
System.out.print("arr[" + (index % this.maxSize) + "]=" + this.arr[index % this.maxSize] + "\t");
}
System.out.println();
}
public int showFront(){
// Empty before displaying the header element
if(isEmpty()){
throw new RuntimeException("The queue is empty and there is no leader");
}
//The direct front is the head of the team
return arr[this.front];
}
}
- Console test
package com.kevin.circlequeueDemo;
import java.util.Scanner;
/**
* @author : kevin ding
* @date : 2022/2/10 0:27
* @description :
*/
public class CircleQueueTest {
public static void main(String[] args) {
System.out.println("Simulate a circular queue through an array...");
// 1. Create a Queue through the Queue class
CircleQueue queue = new CircleQueue(4);
// 2. Write an interface to verify the queue function
boolean loop = true;
char choose = ' ';
Scanner sc = new Scanner(System.in);
while(loop){
System.out.println("a(add): Add data to queue");
System.out.println("g(get): Get data from queue");
System.out.println("h(head): Show team leader elements");
System.out.println("s(show): Show all queue elements");
System.out.println("e(exit): sign out");
System.out.println("Please enter the functions you need to complete:");
// Receive an input from the console
choose = sc.next().charAt(0);
// Judge choose operation
switch (choose){
case 'a':
System.out.println("Please enter the data to insert:");
int num = sc.nextInt();
queue.addDataToQueue(num);
System.out.println();
break;
case 'g':
try{
int data = queue.getDataFromQueue();
System.out.println("The extracted data is:" + data);
}catch (Exception ex){
System.out.println(ex.getMessage());
}
System.out.println();
break;
case 'h':
try {
int frontData = queue.showFront();
System.out.println("The header of the queue is:" + frontData);
}catch (Exception ex){
ex.printStackTrace();
}
System.out.println();
break;
case 's':
queue.showQueue();
System.out.println();
break;
case 'e':
loop = false;
System.out.println();
break;
default:
break;
}
}
sc.close();
System.out.println("Program exit....");
}
}