688. Knight's probability on the chessboard

2022.2.1 one question per day

Title Description

On an n x n chess board, a knight starts from a row (column) and tries to make k moves. Rows and columns start at 0, so the upper left cell is (0,0) and the lower right cell is (n - 1, n - 1).

Chess knight has 8 possible walking methods, as shown in the figure below. Each move is two cells in the basic direction, and then one cell in the orthogonal direction.

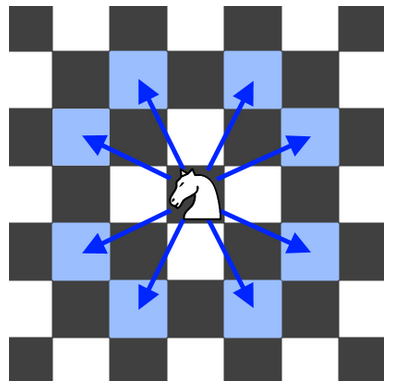
Every time the knight wants to move, it will randomly choose one of the eight possible moves (even if the piece will leave the chessboard) and move there.

The knight continues to move until it takes k steps or leaves the chessboard.

Returns the probability that the knight will remain on the chessboard after the chessboard stops moving.

Example 1:

Input: n = 3, k = 2, row = 0, column = 0
Output: 0.0625
Explanation: there are two steps (to (1,2), (2,1)) to keep the knight on the chessboard.
In each position, there are also two movements that can keep the knight on the chessboard.
The total probability of a knight remaining on the chessboard is 0.0625.

Example 2:

Input: n = 1, k = 0, row = 0, column = 0
Output: 1.00000

Tips:

1 <= n <= 25
0 <= k <= 100
0 <= row, column <= n

Source: LeetCode
Link: https://leetcode-cn.com/problems/knight-probability-in-chessboard
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

Memory search
It should be noted that the data range can only be passed by using double

class Solution {
    int n;
    int[][] dir = {{1,2}, {-1,2}, {1,-2}, {-1,-2}, {2,1}, {2,-1}, {-2,1}, {-2,-1}};
    int res = 0;
    double[][][] graph;
    public double knightProbability(int n, int k, int row, int column) {
        //First of all, you should understand the question. You can't move outside the chessboard
        //Looking at the first example, the probability is 2 * 2 / 8 * 8 = 0.0625
        //In all 64 cases of movement, 4 can be left on the chessboard,
        //This gives us an idea
        //The total case is the k-th power of 8, and several cases can be left on the chessboard,
        //You can traverse every point on the chessboard and count how many situations each point can stay on the chessboard
        //Then start counting from the starting point
        
        //It will time out. You have to add a memory
        this.n = n;
        graph = new double[n][n][k + 1];
        double temp = dfs(row, column, k);
        //System.out.println(temp);
        return (double)temp / Math.pow(8, k);
    }

    public double dfs(int x, int y, int step){
        if(step == 0)
            return 1;
        if(step <= 0)
            return 0;
        if(graph[x][y][step] != 0)
            return graph[x][y][step];
        for(int[] d : dir){
            int nx = x + d[0];
            int ny = y + d[1];
            if(nx < 0 || ny < 0 || nx >= n || ny >= n)
                continue;
            graph[x][y][step] += dfs(nx, ny, step - 1);
        }
        return graph[x][y][step];
    }
}

Or write it as dynamic programming

class Solution {
    int[][] dir = {{1,2}, {-1,2}, {1,-2}, {-1,-2}, {2,1}, {2,-1}, {-2,1}, {-2,-1}};
    public double knightProbability(int n, int k, int row, int column) {
        //dynamic programming
        //dp[i][j][k] represents the probability of remaining on the chessboard when i,j points and the remaining steps are K

        double[][][] dp = new double[n][n][k + 1];
        for(int step = 0; step <= k; step++){
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    if(step == 0)
                        dp[i][j][0] = 1;
                    else{
                        for(int[] d : dir){
                            int x = i + d[0];
                            int y = j + d[1];
                            if(x < 0 || y < 0 || x >= n || y >= n)
                                continue;
                            dp[i][j][step] += dp[x][y][step - 1] / 8;
                        }
                    }
                }
            }
        }
        return dp[row][column][k];
    }
}

1791. Find the central node of the star chart

2022.2.18 one question per day

Title Description

There is an undirected star graph, which is composed of N nodes numbered from 1 to n. The star graph has a central node and exactly n - 1 edges connect the central node with each other.

Give you a two-dimensional integer array edges, where edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and VI. Please find and return the central node of the star graph represented by edges.

Example 1:

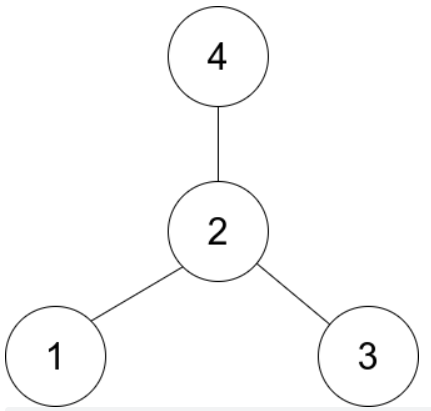
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: as shown in the figure above, node 2 is connected with every other node, so node 2 is the central node.

Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1

Tips:

3 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
The edges given by the title data represent an effective star graph

Source: LeetCode
Link: https://leetcode-cn.com/problems/find-center-of-star-graph
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

class Solution {
    public int findCenter(int[][] edges) {
        //Because it is a star graph, the number of edges is fixed, and each point has only one edge with the central node
        //So just look at which point connects the two sides

        //One of the two sides must have the same number, so just find the same number
        if(edges[0][0] == edges[1][0] || edges[0][0] == edges[1][1])
            return edges[0][0];
        else
            return edges[0][1];
    }
}

969. Pancake sorting

2022.2.19 one question per day

Title Description

Give you an integer array arr, please use pancake flip to sort the array.

The execution process of a pancake flip is as follows:

Select an integer k ，1 <= k <= arr.length
 Anti rotor array arr[0...k-1](Subscript from 0)

For example, arr = [3,2,1,4], select k = 3 to flip the pancake once, reverse the rotor array [3,2,1], and get arr = [1,2,3,4].

Return the k-value sequence corresponding to the pancake flipping operation that can make arr orderly in the form of array. Any valid answer that sorts the array and flips the array within 10 * arr.length will be judged to be correct.

Example 1:

Input: [3,2,4,1]
Output: [4,2,4,3]
Explanation:
We performed four pancake flips with k values of 4, 2, 4, and 3, respectively.
Initial state arr = [3, 2, 4, 1]
After the first flip (k = 4): arr = [1, 4, 2, 3]
After the second flip (k = 2): arr = [4, 1, 2, 3]
After the third flip (k = 4): arr = [3, 2, 1, 4]
After the fourth flip (k = 3): arr = [1, 2, 3, 4], the sorting has been completed.

Example 2:

Input: [1,2,3]
Output: []
Explanation:
The input has been sorted, so there is no need to flip anything.
Please note that other possible answers, such as [3, 3], will also be judged to be correct.

Tips:

1 <= arr.length <= 100
1 <= arr[i] <= arr.length
All integers in arr are different from each other (that is, arr is an arrangement of integers from 1 to arr.length)

Source: LeetCode
Link: https://leetcode-cn.com/problems/pancake-sorting
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

class Solution {
    public List<Integer> pancakeSort(int[] arr) {
        //How to flip it? Change the current maximum number to the first, and then flip it to the back
        //For example, the first example 3 2 4 1
        //Flip the first three 4 2 3 1, and then flip the first four 1 3 2 4
        //Then flip the first two 3 1 2 4 and the first three 2 1 3 4
        //Then turn over the first two. The method is feasible

        int l = arr.length;
        int max = l;
        int idx = l - 1;
        List<Integer> list = new ArrayList<>();
        while(idx > 0){
            int temp = 0;
            for(int i = 0; i <= idx; i++){
                if(arr[i] == max){
                    temp = i;
                }
            }
            if(temp != idx){
                reverse(arr, temp, idx);
                list.add(temp + 1);
                list.add(idx + 1);
            }
            max--;
            idx--;
        }
        return list;
    }
    public void reverse(int[] arr, int temp, int idx){
        int left = 0;
        int right = temp;
        while(left < right){
            int t = arr[left];
            arr[left++] = arr[right];
            arr[right--] = t;
        }
        left = 0;
        right = idx;
        while(left < right){
            int t = arr[left];
            arr[left++] = arr[right];
            arr[right--] = t;
        }
    }
}