preface

If you think the article is helpful, please leave some praise and collection. Pay attention to xiaoleng and read more dry goods learning articles

★ this is Xiao Leng's blog ‡ see the column for good articles on high-quality technology The official account of the individual, sharing some technical articles, and the pit encountered. Current series: data structure series Source code git warehouse Data structure code address Code Git warehouse address

catalogue

• • preface
    • Sequential storage binary tree
    • • The concept of sequential storage binary tree
      • Features of sequential storage binary tree:
      • Sequential storage binary tree traversal
      • code implementation

Sequential storage binary tree

The concept of sequential storage binary tree

From the perspective of data storage, the storage methods of array and tree can be converted to each other, that is, array can be converted into tree and tree can also be converted into array,

The nodes of the binary tree in the figure above are required to store the ARR in the form of array: [1, 2, 3, 4, 5, 6, 6] 2) it is required that when traversing the array arr, the nodes can still be traversed in the way of pre order traversal, middle order traversal and post order traversal

Features of sequential storage binary tree:

1. Sequential binary trees usually only consider complete binary trees
2. The left child node of the nth element is 2 * n + 1 (calculation formula)
3. The right child node of the nth element is 2 * n + 2 (calculation formula)
4. The parent node of the nth element is (n-1) / 2
5. n: indicates the number of elements in the binary tree

Sequential storage binary tree traversal

demand

Give you an array {1,2,3,4,5,6,7}, which is required to be traversed in the way of binary tree preorder traversal.

The result of preorder traversal should be 1,2,4,5,3,6,7

Coding idea

The idea of judgment here is to transform an array into a tree,

Array: 1,2,3,4,5,6,7

Tree (as shown below)

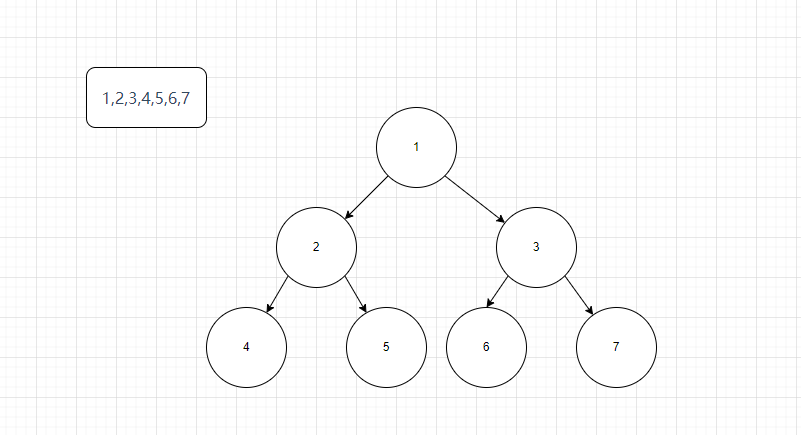
• The left child node of the nth element is 2 * n + 1 (calculation formula)
• The right child node of the nth element is 2 * n + 2 (calculation formula)

We can use this formula to prove the correctness of array to tree

For example, we need to calculate the position of two. 2 is the left child node of 1, 1 is the element with subscript 0, 2 * 0 + 1. Apply the formula = 1, and the following nodes are the same

code implementation

package com.hyc.DataStructure.tree;

/**
 * @projectName: DataStructure
 * @package: com.hyc.DataStructure.tree
 * @className: ArrayTreeDemo
 * @author: Cold Huanyuan doorwatcher
 * @description: TODO
 * @date: 2022/2/4 19:07
 * @version: 1.0
 */
public class ArrayTreeDemo {
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7};
        ArrayTree arrayTree = new ArrayTree(arr);
        //452 6731
        arrayTree.postOrder(0);
    }
}

class ArrayTree {
    private int[] arr;

    public ArrayTree(int[] arr) {
        this.arr = arr;
    }

    //    Preorder traversal of sequential storage tree
    // Traverse the formula to find the nth left node n*2+1 of N and the nth right node n*2+2 of n
    // The input parameter int index is to start traversing to the root node, which is the array subscript 0
    public void preOrder(int index) {
        //Non null judgment avoids null pointers
        if (arr == null || arr.length == 0) {
            System.out.println("The tree is empty and cannot be traversed");
        }
        //    Preorder traversal first outputs itself
        System.out.println(arr[index]);
        //    Then recursively traverse the left node
        //Judge whether the index is out of bounds
        if ((2 * index + 1) < arr.length) {
            preOrder(index * 2 + 1);
        }
        //    Then recursively traverse the right node
        //Judge whether the index is out of bounds
        if ((2 * index + 2) < arr.length) {
            preOrder(index * 2 + 2);
        }
    }

    public void infixOrder(int index) {
        //Non null judgment avoids null pointers
        if (arr == null || arr.length == 0) {
            System.out.println("The tree is empty and cannot be traversed");
        }
        //    Recursively traverse the left node
        //Judge whether the index is out of bounds
        if ((2 * index + 1) < arr.length) {
            infixOrder(index * 2 + 1);
        }
        //    Middle order traversal output
        System.out.println(arr[index]);
        //    Recursively traverse the right node
        //Judge whether the index is out of bounds
        if ((2 * index + 2) < arr.length) {
            infixOrder(index * 2 + 2);
        }
    }

    public void postOrder(int index) {
        //Non null judgment avoids null pointers
        if (arr == null || arr.length == 0) {
            System.out.println("The tree is empty and cannot be traversed");
        }
        //    Recursively traverse the left node
        //Judge whether the index is out of bounds
        if ((2 * index + 1) < arr.length) {
            postOrder(index * 2 + 1);
        }
        //    Recursively traverse the right node
        //Judge whether the index is out of bounds
        if ((2 * index + 2) < arr.length) {
            postOrder(index * 2 + 2);
        }
        //    Post order traversal output
        System.out.println(arr[index]);
    }
}

Here, we first understand the sequential storage binary tree, and master its node calculation ideas and traversal ideas. When sorting the article heap after a small cold, we will use the knowledge points and preheat in advance