catalogue

1. Storage structure and definition of single linked list

storage structure

Function definition

Example: Student transcript

2. Function definition

2.1 initialization function

2.2 empty judgment function

2.3 destruction function

2.4 emptying function

2.5 finding table length function

2.6 search function by location

2.7} find function by value

2.8 insert function

2.9 delete function

2.10 create linked list - head interpolation / front interpolation

2.11 create linked list tail insertion method

1. Storage structure and definition of single linked list

storage structure

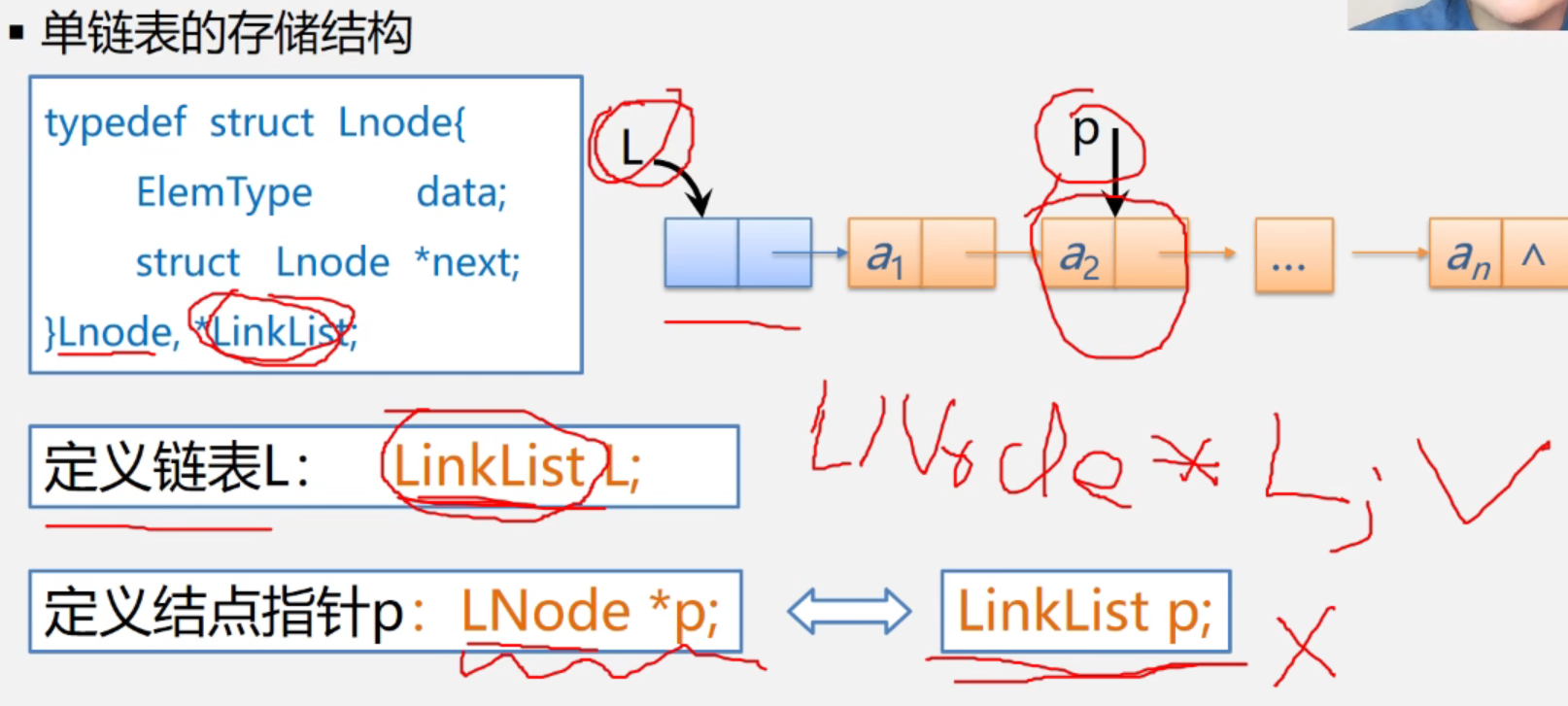
Typedef Description: typedef int status. The first is the type, and the second is the given object. In the following example, a pointer Linklist is given, and then Linklist can be directly used to represent the pointers to nodes similar to L and p in the figure. Linklist L = Lnode *L, simpler.

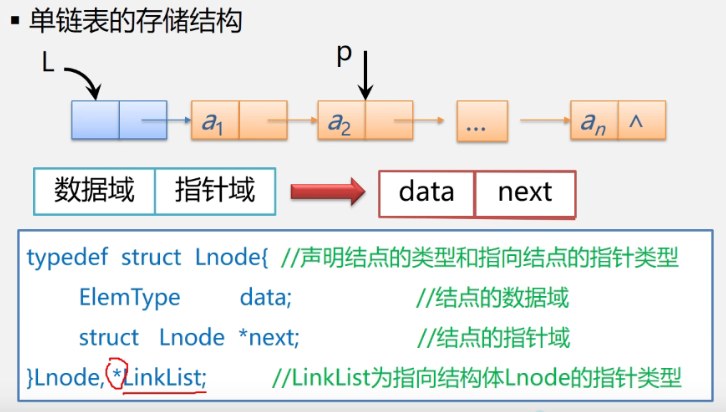
Function definition

Linklist is generally used for linked list and LNode is used for defining pointer. Actually, it's all right, but I'm more used to it.

Example: Student transcript

For unified operation, data fields are generally defined separately. In this way, there are only data field and pointer field in Lnode.  

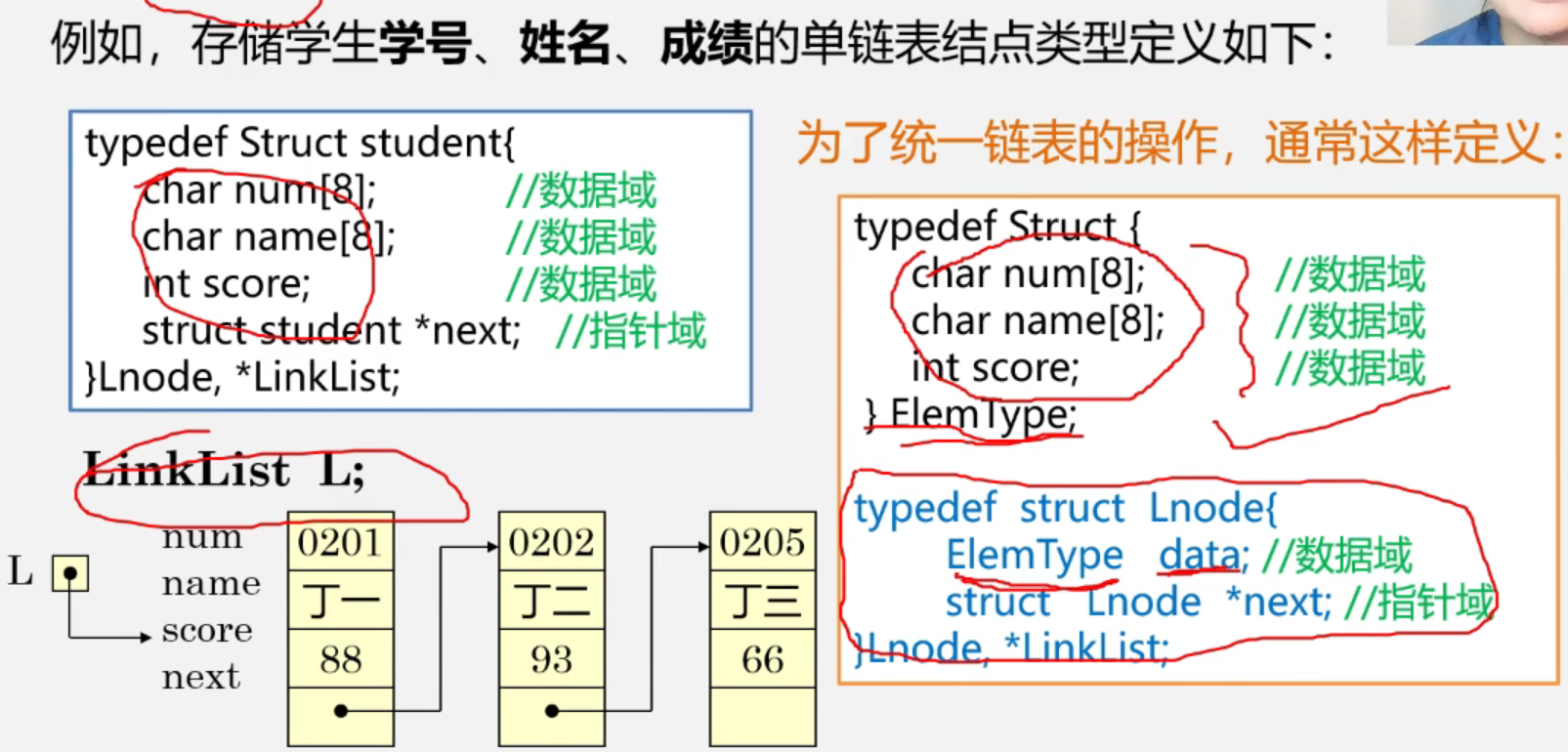
2. Function definition

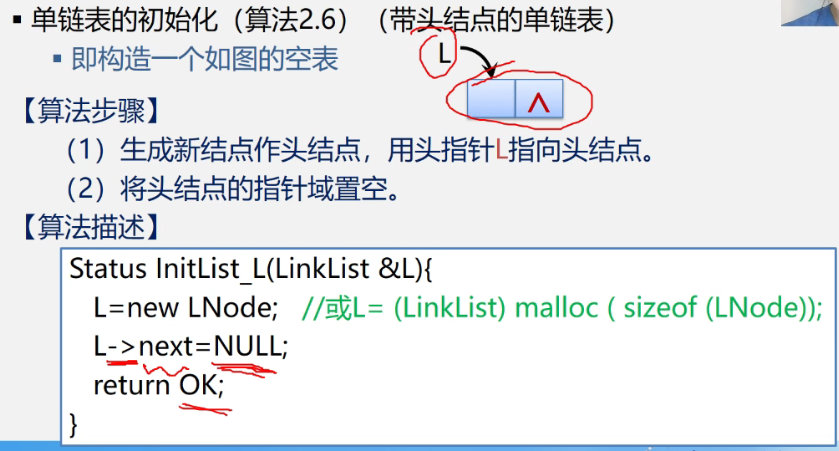
2.1 initialization function

Note: Linklist itself is a pointer, so you don't need to add *. The int * used in the previous sequential storage is an int pointer.

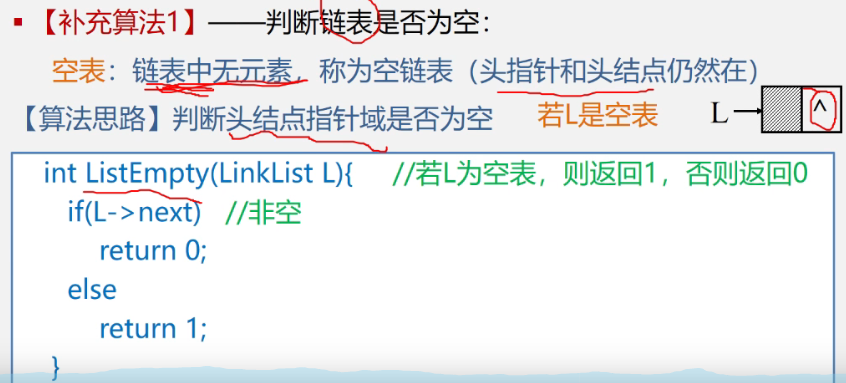
2.2 empty judgment function

2.3 destruction function

thinking

Use a new pointer to point to the head node, then make the original pointer point to the next node, delete the area pointed by the new pointer, and so on.

Release operation:

C++: new with delete p

C: malloc(sizeof()) with free(p)

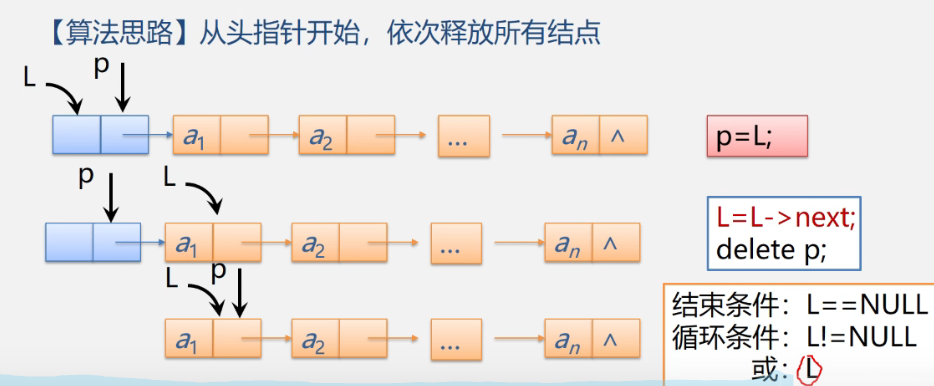
Code (C + +)

Note: when defining a new pointer p, it is written as Linklist *p, which is not standardized. Node pointer definition should be Lnode *p

Status DestroyList_L(Linklist &L){
    Lnode *p;
    while(L){
        p=L;
        L=L->next;
        delete p;//free(p);
    }
    return OK;
}

2.4 emptying function

thinking

Step by step is simpler than step by step, but the code implementation is more complex. So still use the teacher's method.

code

Status ClearList(Linklist &L){
    Lnode *p,*q;
    p = L->next;
    while(p){
        q = p->next;
        delete p;
        p = q；
    }
    L->next = NULL;
    return OK;
}

2.5 finding table length function

Start from the first element node and cycle back to the next field. If p is not empty, the table length is + 1

code

Status ListLength(Linklist L){
    Lnode *p;
    p = L->next;
    int i=0;
    while(p){
        i++;
        p = p->next;
    }
    return i;
}

2.6 search function by location

Train of thought

code

Status GetElem(Linklist L, int i, Elemtype &e){
    Lnode *p;
    p = L->next;
    int j = 1;
    while(p&&j<i){
        j++;
        p = p->next;
    }
    if(!p||j>i) return ERROR;//! p means i is too large and not found. J > i means i is too small. It may be 0 or negative
    e = p->data;
    return e;
}

2.7} find function by value

Code (return address pointer)

Lnode *LocateElem(Linklist L, Elemtype e){
    Lnode *p;
    p = L->next;
    while(p && p->data!=e)
        p = p->next;
    if(!p) return ERROR;
    return p;
}

Code (return location)

Status LocateElem(Linklist L, Elemtype e){
    Lnode *p;
    p = L->next;
    int i = 1;
    while(p && p->data!=e){
        p = p->next;
        i++;
    }
    if(!p) return ERROR;
    return i;
}

Time complexity O(n)

2.8 insert function

thinking

Reasonable position of insertion: 1-n+1. If it is inserted in bit n+1, the pointer p should be in bit n after passing through the loop. Therefore, when initializing, p=L head node and j=0 (bit 0) can be inserted into the first bit.

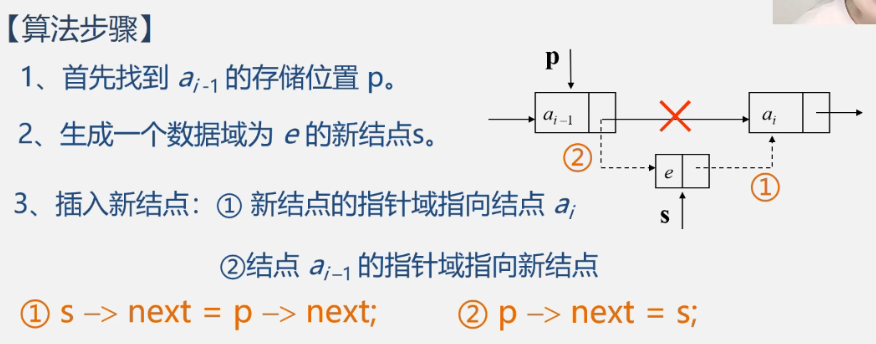
code

Status ListInsert(Linklist &L, int i, Elemtype e){
    Lnode *p = L;//Initialization is on the header node L, not the first element node
    int j = 0;
    while(p && j<i-1){
        j++;
        p = p->next;
    }
    if(!p||j>i) return ERROR;//If the length exceeds + 1 or i is not a positive number, an error will be reported
    s = new Lnode; s->data = e;//Create a new node space storage e
    s->next = p->next;
    p->next = s;//Re bridging
    return OK;
}

Time complexity O(n) because you need to find it from scratch

2.9 delete function

thinking

Before deleting bit i, connect the next of bit i-1 to bit i+1, and then release it.

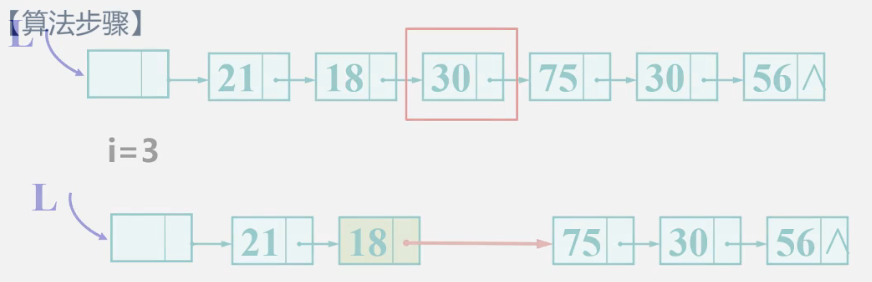
code

Status DeleteElem(Linklist &L, int i, Elemtype &e){//**ElemType & E optional**
    Lnode *p = L;
    Lnode *s;
    int j = 0;
    while(p->next && j<i-1){
        j++;
        p = p->next;//p is now the direct precursor of the i-th bit to be deleted
    }
    if(!(p->next)||j>i-1) return ERROR;
    s = p->next;  //Pos i tion s of the record to be deleted
    p->next = p->next->next;  //Re bridging from i-1 to i+1
    e = s->data; //**Optional * * the deleted value of the record, which can be used to view
    delete s;
    return OK;
}

Time complexity O(n) because you need to find it from scratch

2.10 create linked list - head interpolation / front interpolation

thinking

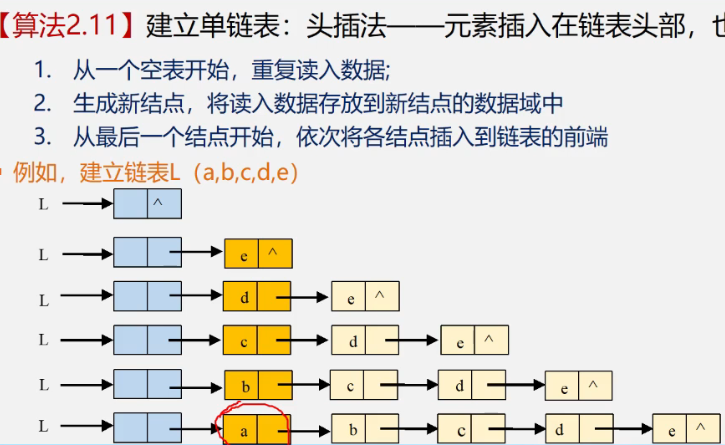
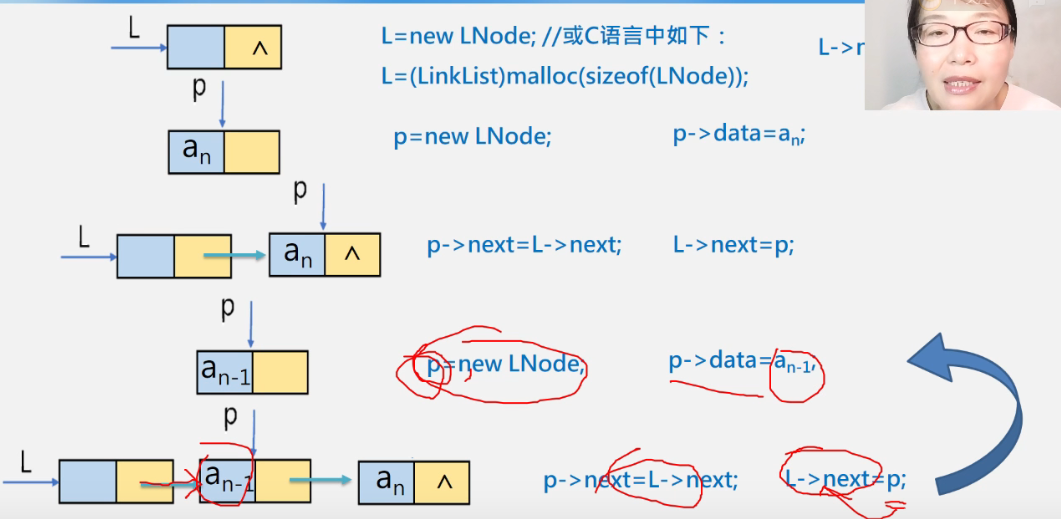
code

void CreateList(Linklist &L, int n){
    L = new Lnode; //L = (Linklist)malloc(sizeof(Lnode));
    L->next = NULL;
    for(i = n; i > 0; i--){
        p = new Lnode; //L = (Lnode*)malloc(sizeof(Lnode));
        cin>>p->data; //scanf(&p->data);
        p->next = L->next;
        L->next = p; //Re bridging
    }
}

Time complexity O(n), executed n+1 times in for.

2.11 create linked list tail insertion method

thinking

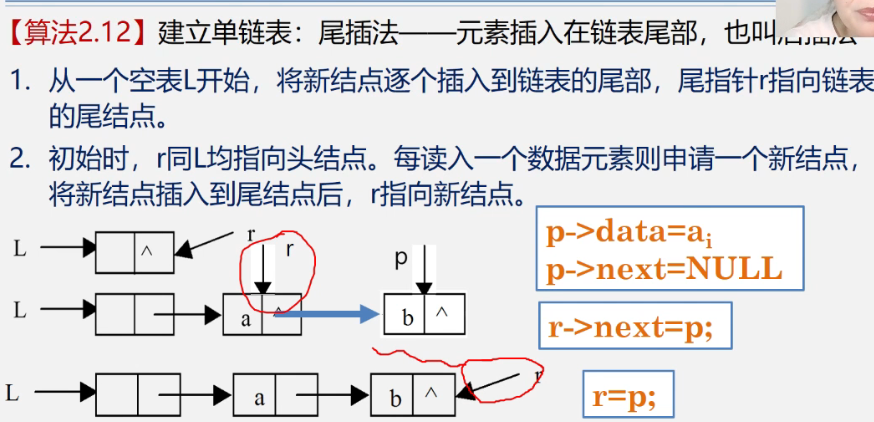
Code

void CreateList(Linklist &L, int n){
    L = new Lnode; // L = (Linklist)malloc(sizeof(Lnode));
    L->next = NULL;
    Lnode *r = L;
    for(i = 0; i < n; i++){
        p = new Lnode; cin>>p->data; p->next = NULL;
        r->next = p; //Connect p to the end
        r = p; //r points last
    }
}