Python WeChat Subscription Applet Course Video
https://edu.csdn.net/course/detail/36074
Python Actual Quantitative Transaction Finance System
https://edu.csdn.net/course/detail/35475
Preface:
This article mainly explains some preparations I have made in learning the sorting algorithm in Java development environment, and personal experiences. I will summarize this article as my own summary and notes on the sorting algorithm understanding.
The content is mainly about the introduction, principle, dynamic and static illustrations and analysis of source code implementation of the ten classical sorting algorithms.
As a programmer, we all know that data structures and algorithms are mainly used in C language at first, but there are few cases of using algorithms in Java language, so sorting algorithms in Java development environment are sorted out for everyone to learn and explore.
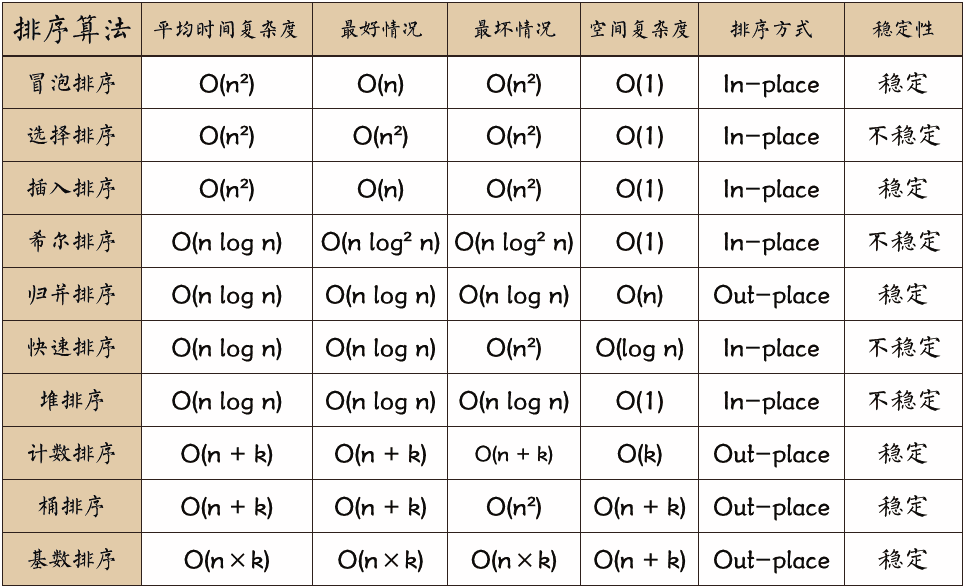
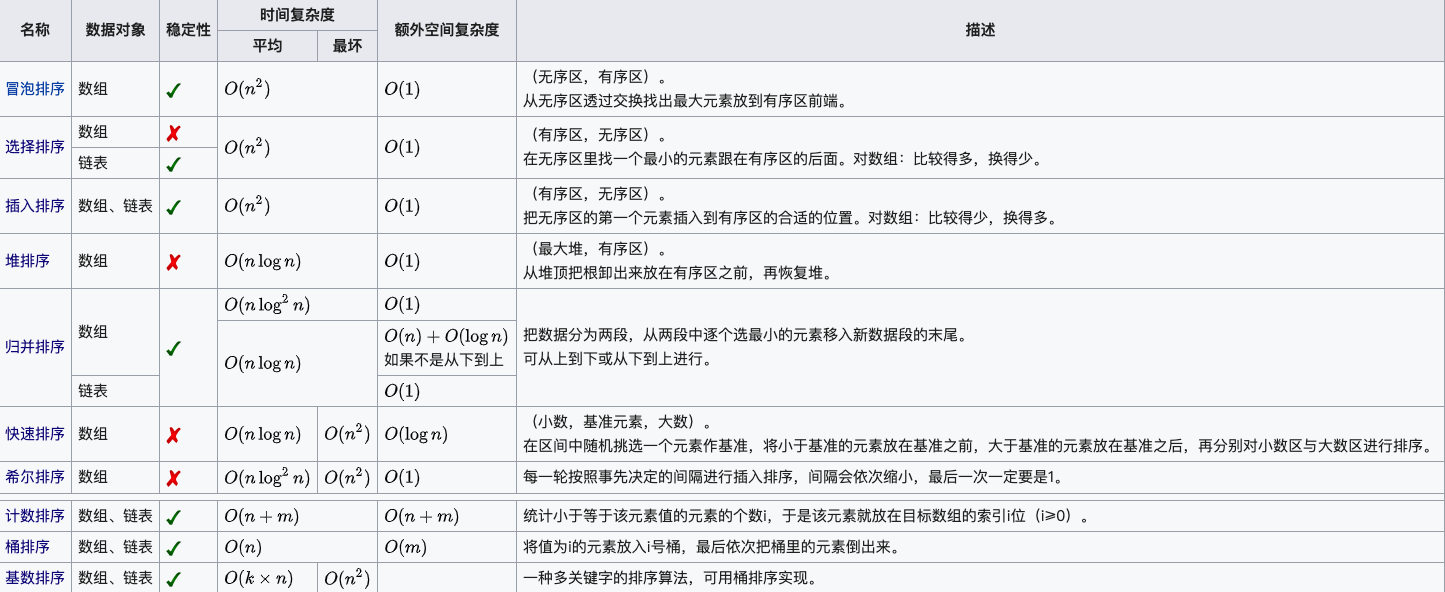
1. Sorting algorithm
1. Overview of sorting algorithm (Baidu Encyclopedia):
The so-called sorting algorithm means that one or more sets of data are reordered according to a given pattern by a specific algorithm factor. This new sequence follows certain rules and reflects certain rules. Therefore, the processed data is easy to filter and calculate, and greatly improves the calculation efficiency. For sorting, we first require some stability, that is, when two identical elements appear in a sequence at the same time, after a certain sorting algorithm, the relative position of both before and after sorting does not change. In other words, even two identical elements are different in the sorting process and confusion is not allowed.
2. Sorting algorithm in Data Structure and Algorithms
Common sorting algorithms are insertion sort, Hill sort, selection sort, bubble sort, merge sort, quick sort, heap sort, cardinality sort, and so on.
Algorithmic illustrations (novice bird tutorial borrowed):
Graphical analysis:
3. Algorithmic Analysis
Time Complexity
Square Order (O(n2)) Sorting All kinds of simple sorting: direct insertion, direct selection, and bubble sort.
Linear logarithmic order (O(nlog2n)) sorting quick sort, heap sort and merge sort;
O(n1+) sorting, is a constant between 0 and 1. Shell Sort
Linear order (O(n)) sort cardinality sort, in addition to barrel, box sort.
About stability
Stable sorting algorithms: bubble sorting, insert sorting, merge sorting, and base sorting.
Not a stable sorting algorithm: select sorting, quick sorting, Hill sorting, heap sorting.
Noun Interpretation:
- n: Data size
- k: Number of buckets
- In-place: Constant memory, no extra memory
- Out-place: Extra memory usage
- Stability: The order of the two equal key values after sorting is the same as before sorting
- Average time complexity refers to the running time of the algorithm when all possible input instances occur with equal probability
- Worst-case time complexity, generally discussed, is the worst-case time complexity, because in the worst-case case time complexity is the boundary at which the algorithm runs on any input instance, which ensures that the algorithm does not run longer than in the worst-case case case.
- Whether the average time complexity is the same as the worst time complexity depends on the algorithm.
2. Top 10 Classic Sorting Algorithms (Java Development Edition)
PS: Cases take the array {15, 63, 97, 12, 235, 66} sort as an example
1. Bubble sort
Bubble Sort is a simpler sorting algorithm in computer science.
It repeatedly visits the column of elements to be sorted, compares two adjacent elements in turn, and swaps them if the order (large to small, Z to A) is wrong. The work of visiting an element is repeated until no adjacent elements need to be exchanged, that is, the element column has been sorted.
The algorithm's name comes from the fact that smaller elements "float" slowly to the top of a number of columns (ascending or descending) by exchange, just as the bubbles of carbon dioxide in a carbonated drink eventually float to the top, hence the name "bubble sort".
1.1 Implementation Principle
- Compare adjacent elements. If the first one is bigger than the second, swap the two.
- Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. At this point, the last element should be the maximum number.
- Repeat the above steps for all elements except the last one.
- Continue repeating the above steps for fewer and fewer elements each time until no pair of numbers need to be compared.

1.2 Kinematic Demo
1.3 Instance Show
1 import java.util.Arrays;
2 public class BubbleSort {
3 public static void main(String[] args) {
4 int[] arrays =new int[]{15,63,97,12,235,66};
5 for (int i=0;i1;i++){
6
7 // Controlling the number of comparisons, exchanging the three to achieve sorting
8 for(int j=0;j1-i;j++){
9 if (arrays[j] > arrays[j+1]){
10 int temp = 0;//Similar to empty bucket
11 temp = arrays[j]; //Water in bucket A is poured into empty bucket C
12 arrays[j] = arrays[j+1];//Pour the water from bucket B into bucket A
13 arrays[j+1] = temp;//Pour C bucket of water into B bucket
14 }
15 }
16 }
17 System.out.println(Arrays.toString(arrays));
18 }
19 }
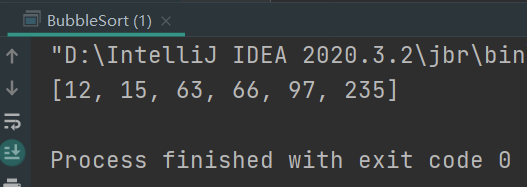
Sort results display:
2. Quick Sort
Quicksort, computer science vocabulary, applicable fields Pascal, c++ and other languages, is an improvement of the bubble sort algorithm.
2.1 Implementation Principles
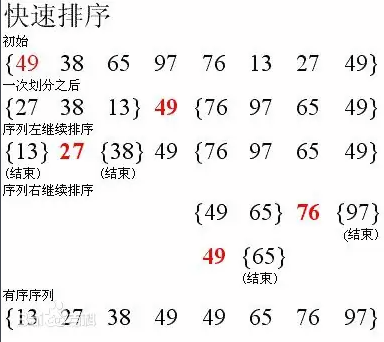
Quick sorting is an improvement on bubble sorting. The data to be sorted is divided into two separate parts by one-time sorting, in which all the data in one part is smaller than all the data in the other part. Then the two parts are sorted separately by this method, and the whole sorting process can be done recursively so that the whole data becomes an ordered sequence.
2.2 Kinematic Demo
2.3 Instance Show
1 import java.util.Arrays;
2 public class QuickSort {
3 public static void main(String[] args) {
4 int[] arrays = new int[]{15,63,97,12,235,66};
5 sort(arrays,0,arrays.length-1);
6 System.out.println(Arrays.toString(arrays));
7 }
8 public static void sort(int[] arrays,int left,int right){
9 int l = left;
10 int r = right;
11
12 int pivot = arrays[(left+right)/2];
13 int temp = 0;
14 while (l15
16 //Find below the middle value on the left
17 while(arrays[l]18 l++;
19 }
20 //Query right less than median
21 while (arrays[r]>pivot){
22 r--;
23 }
24 if (l>=r){
25 break;
26 }
27 temp = arrays[l];
28 arrays[l] = arrays[r];
29 arrays[r] = temp;
30
31 // Exchanged data arrays[l] = pivot
32 if (arrays[l]==pivot){
33 r--;
34 }
35 if (arrays[r]==pivot){
36 l++;
37 }
38 if (r==l){
39 l++;
40 r--;
41 }
42 if (left43 sort(arrays,left,r);
44 }
45 if (right>l){
46 sort(arrays,l,right);
47 }
48 }
49 }
50 }
Sort results display:
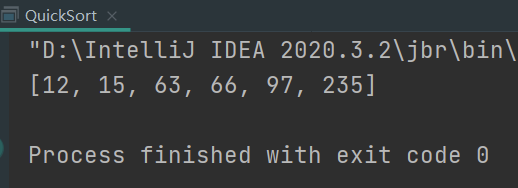
3. Cardinal Sorting
radix sort is a distribution sort, also known as bucket sort or bin sort. As the name implies, it is sorted by some information about the key values. Element Allocation To some "barrels" in order to achieve the sorting effect, the cardinality sorting method is a stable sort. Time Complexity Is O (nlog) ® m), where r is the cardinality to be used and m is the heap number, the cardinality sorting method is more efficient than other stable sorting methods in some cases.
The cardinality order was invented by Herman and Horley in 1887. The idea is to cut integers into different numbers by digits and compare them by digits.
3.1 Implementation Principles
Say that all the values to be compared are set to the same bit length, with the shorter digits preceded by zeros, and then sorted one by one from the top, so that the column becomes an ordered sequence from the lowest to the highest.
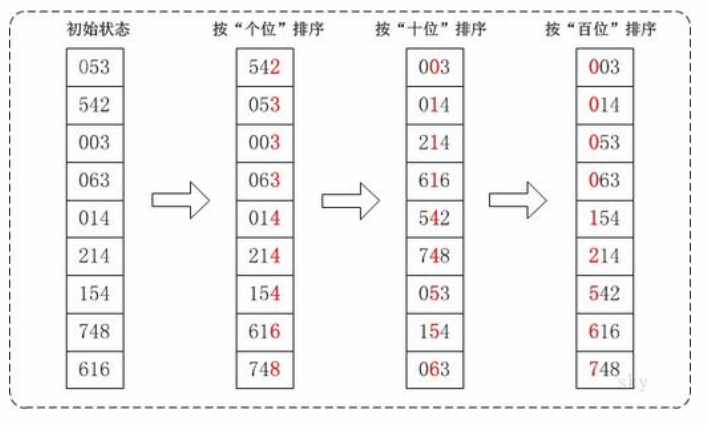
3.2 Kinematic Demo

3.3 Example Show
1 import java.text.SimpleDateFormat;
2 import java.util.Arrays;
3 import java.util.Date;
4
5 public class BasicSort {
6
7 public static void main(String[] args) {
8 int[] arrays = new int[]{15,63,97,12,235,66};
9 SimpleDateFormat simpleDateFormat =new SimpleDateFormat("yyyy-mm-dd HH:MM:ss:SS");
10 System.out.println("Before starting sorting:"+simpleDateFormat.format(new Date()));
11 sort(arrays);
12 System.out.println("End of Sort:"+simpleDateFormat.format(new Date()));
13 }
14
15 // 1. Get the maximum bits of the original sequence
16 // @param arrays
17 public static void sort(int[] arrays){
18
19 // Get the maximum number of bits
20 int max = 0;
21 for(int i=0;i22 if (arrays[i]>max){
23 max = arrays[i];
24 }
25 }
26
27 // Gets the string length, so converts the int type to the string type
28 int maxLength = (max+"").length();
29
30 // Defines a two-dimensional array of 10 barrels, one for each barrel
31 // [[],[],[],[],[]...]
32 int[][] bucket = new int[10][arrays.length];
33
34 // Auxiliary array
35 int[] bucketElementCount = new int[10];
36
37 // Loop to get an unordered column
38 for (int j=0;j39 int locationElement = arrays[j]%10;
40
41 // Place in bucket
42 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j] ;
43 bucketElementCount[locationElement]++;
44 }
45
46 // Walk through each bucket and say that elements are stored in the original array
47 int index = 0;
48 for (int k = 0;k49 if (bucketElementCount[k] !=0){
50 for (int l = 0;l51 arrays[index++] = bucket[k][l];
52 }
53 }
54 bucketElementCount[k] = 0;
55 }
56 System.out.println(Arrays.toString(arrays));
57
58 // First round of comparison for bits
59 for (int j = 0;j60 int locationElement = arrays[j]/1%10;
61
62 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j];
63 bucketElementCount[locationElement]++;
64 }
65
66 // Take it out and put it back into the original array in bucket order
67 int indx = 0;
68 for (int k = 0;k69 if (bucketElementCount[k] !=0){
70 for (int l=0;l71 arrays[indx++] = bucket[k][l];
72 }
73 }
74 bucketElementCount[k] = 0;
75 }
76
77 // Decide Ten Digits
78 for (int j = 0;j79 int locationElement = arrays[j]/10%10;
80
81 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j];
82 bucketElementCount[locationElement]++;
83 }
84
85 // Take it out and put it back into the original array in bucket order
86 indx = 0;
87 for (int k = 0;k88 if (bucketElementCount[k] !=0){
89 for (int l=0;l90 arrays[indx++] = bucket[k][l];
91 }
92 }
93 bucketElementCount[k] = 0;
94 }
95
96 // Get a 100-digit comparison
97 for (int j = 0;j98 int locationElement = arrays[j]/100%10;
99
100 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j];
101 bucketElementCount[locationElement]++;
102 }
103
104 // Take it out and put it back into the original array in bucket order
105 indx = 0;
106 for (int k = 0;k107 if (bucketElementCount[k] !=0){
108 for (int l=0;l109 arrays[indx++] = bucket[k][l];
110 }
111 }
112 bucketElementCount[k] = 0;
113 }
114 System.out.println("Order after cardinality sorting:"+Arrays.toString(arrays));
115 }
116 }
Sort results display:
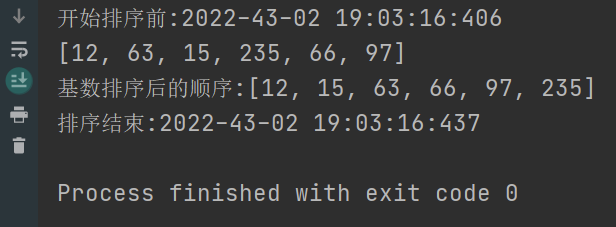
4. Insert Sort
Insert sort, also known as direct insert sort. It is an effective algorithm for sorting a small number of elements. Insert sort is one of the simplest sort The basic idea of this method is to insert a record into an ordered table that has been sorted so as to create a new ordered table with an increase of one record number. In its implementation, a two-tier loop is used, an outer loop finds and moves all elements except the first one, and an inner loop finds and moves an ordered table in front of the current element where it needs to be inserted.
4.1 Implementation Principles
Insert sort works like many people sort first hand poker cards. At first, our left hand was empty and the cards on the table were facing down. Then we take a card from the table each time and insert it in the right position in our left hand. To find the right position for a card, we compare it from right to left with each card that is already in hand. Cards held on the left hand are always sorted. They were originally the top cards in the stack on the table.
Insertion sort refers to the element to be sorted, assuming that the number of the first n-1 (where n>=2) is already in order, inserting the nth number into the previously arranged sequence and finding the appropriate position so that the sequence with the nth number is also in order. Inserting all elements in this way until the entire sequence is ordered is called insertion ordering.
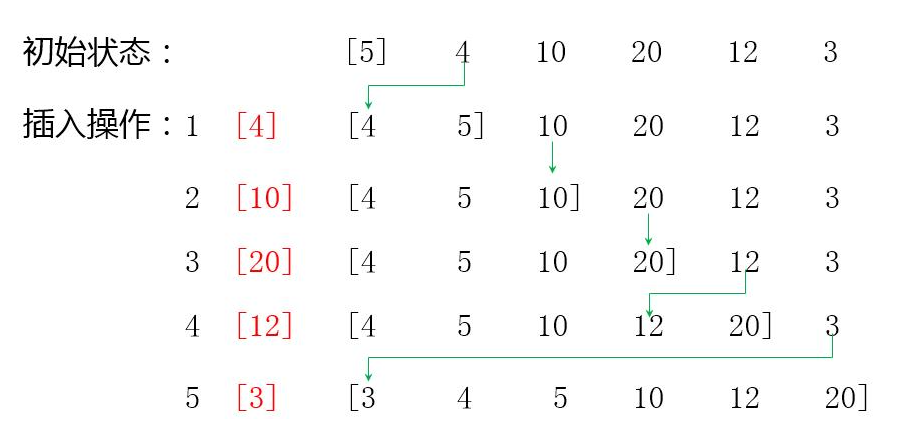
4.2 Kinematic Demo
4.3 Instance Show
1 public class InsertSort {
2 public static void main(String[] args) {
3 int[] array = new int[]{15,63,97,12,235,66};
4 //Control takes every element
5 for(int i=1;i<array.length;i++){
6 //Number of comparisons
7 for (int j=i;j>=1;j--){
8 //Is it smaller than the previous element
9 if (array[j]<array[j-1]){
10 int temp = 0;
11 temp = array[j];
12 array[j] = array[j-1];
13 array[j-1] = temp;
14 }else {
15 //continue and break
16 break;
17 }
18 }
19 }
20 System.out.println("Sorted results:"+ Arrays.toString(array));
21 }
22 }
Sort results display:
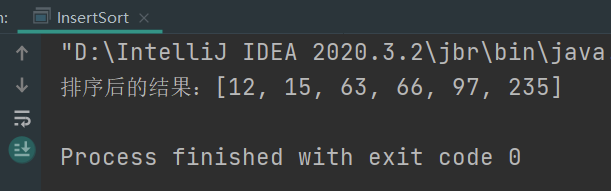
5. Select Sort
Selection sort is simple and intuitive Sorting algorithm . It works like this: the first time it's sorted data elements Select the smallest (or largest) element, store it at the beginning of the sequence, find the smallest (largest) element from the remaining unsorted elements, and place it at the end of the sorted sequence. And so on until all the data elements to be sorted have zero number. Choice sort Is an unstable sorting method.
5.1 Implementation Principles
First time from pending data elements Select the smallest (or largest) element, store it at the beginning of the sequence, find the smallest (largest) element from the remaining unsorted elements, and place it at the end of the sorted sequence. And so on until all the data elements to be sorted have zero number. Choice sort Is an unstable sorting method.
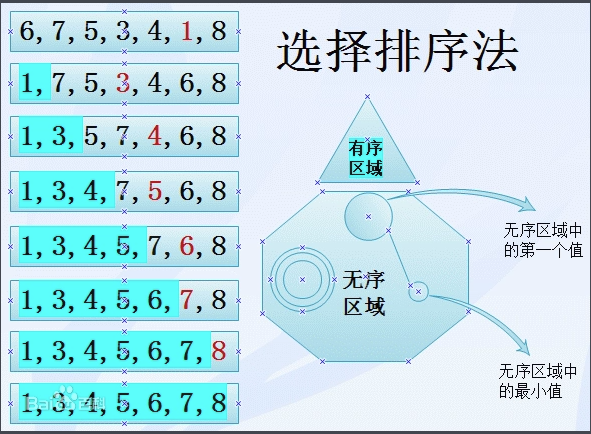
5.2 Kinematic Demo
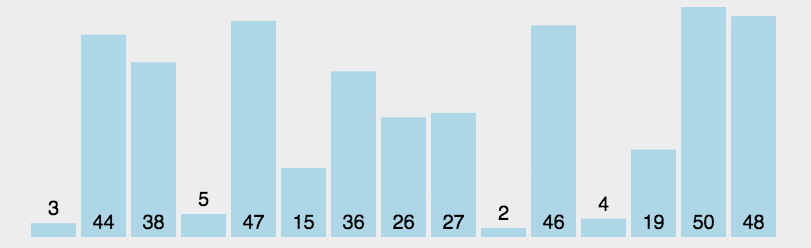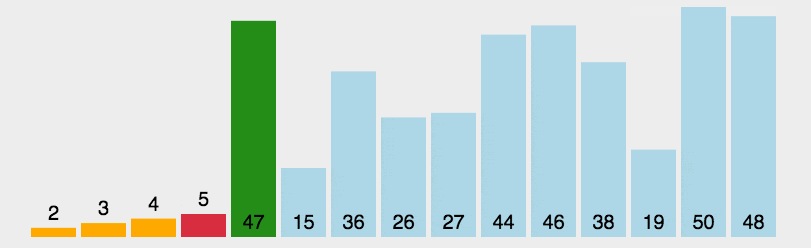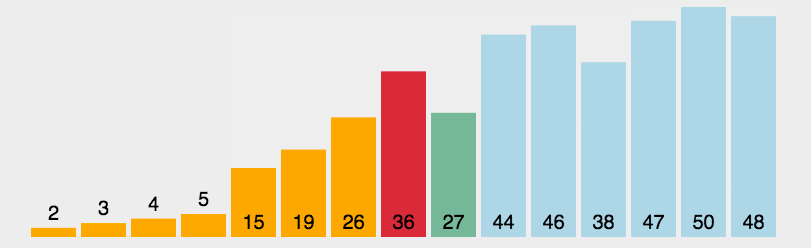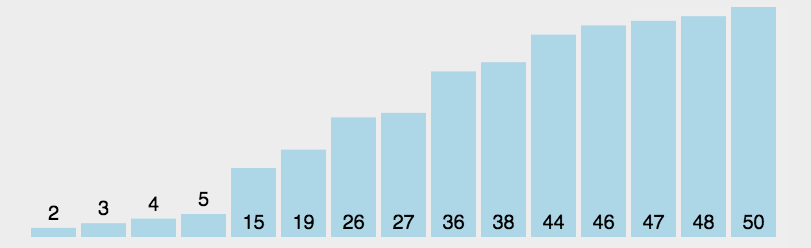
5.3 Instance Show
1 import java.util.Arrays;
2 public class SelectSort {
3 public static void main(String[] args) {
4 int[] arr = new int[]{15,63,97,12,235,66};
5 for (int i=0;i6
7 for (int j=arr.length-1;j>i;j--){
8
9 if (arr[j]10
11 int temp = 0;
12 temp = arr[j];
13 arr[j] = arr[i];
14 arr[i] = temp;
15 }
16 }
17 }
18 System.out.println("Select sorted results:"+ Arrays.toString(arr));
19 }
20 }
Sort results display:
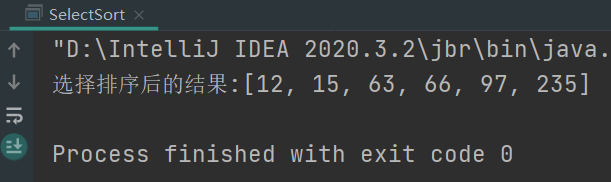
6. Hill Sorting
Shell's Sort, also known as Diminishing Increment Sort, is a more efficient and improved version of the insert sort algorithm. Hill sorting is an unstable sorting algorithm. This method was named after D.L.Shell's introduction in 1959.
Hill sorting uses a direct insertion sorting algorithm to sort each group by an incremental grouping of records by subscripts. As the increment decreases, each group contains more and more keywords. When the increment decreases to 1, the entire file is divided into groups and the algorithm terminates.
6.1 Implementation Principles
First take an integer d1 less than n as the first increment To group all records of a file. All records whose distances are multiples of d1 are placed in the same group. Start in groups Insert Sort Directly ; Then, take the second increment d2
Half of the normal initial sequence is increment And halve each time until the increment is 1.
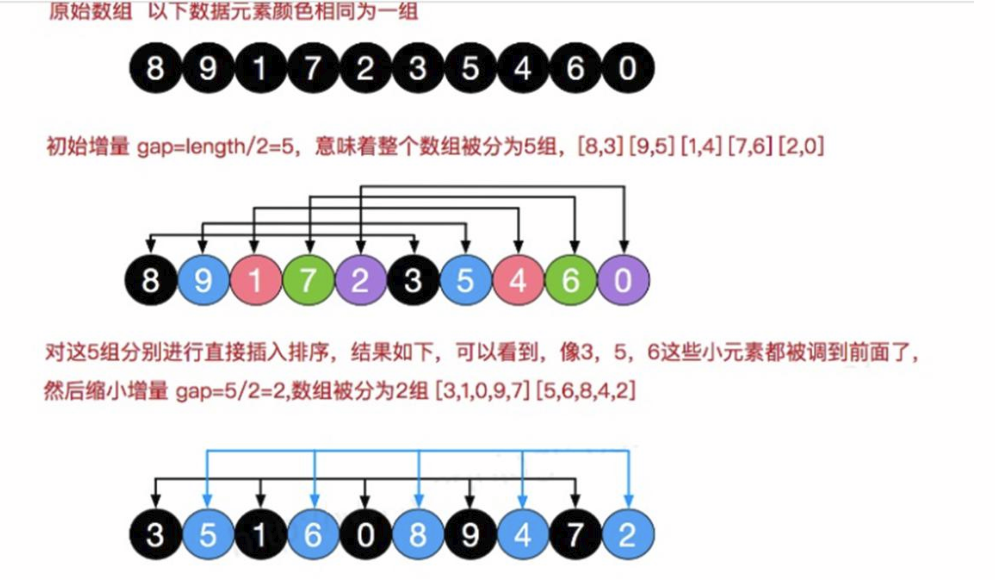
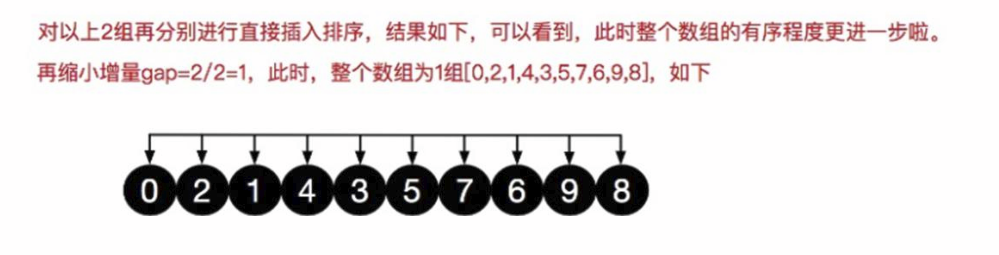

6.2 Kinematic Demo
6.3 Example Show
1 import java.util.Arrays;
2 public class ShellSort {
3 public static void main(String[] args) {
4 int[] array = new int[]{15,63,97,12,235,66};
5
6 // Achieve incremental change
7 for (int gap = array.length/2;gap>0;gap/=2){
8
9 for (int i=gap;i<array.length;i++){
10
11 for (int j=i-gap;j>=0;j-=gap){
12 if (array[j]>array[j+gap]){
13 int temp = 0;
14 temp = array[j];
15 array[j] = array[j+gap];
16 array[j+gap] = temp;
17 }
18 }
19 }
20 }
21 System.out.println(Arrays.toString(array));
22 }
23 }
Sort results display:
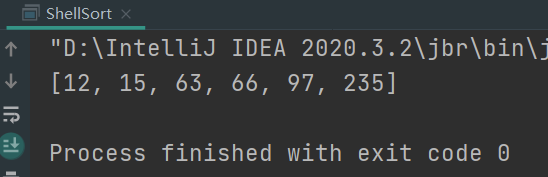
7. Merge Sort
Merge Sort is an effective and stable sorting algorithm based on merge operation. It is a very typical application of Divide and Conquer. Merge the existing ordered subsequences to obtain a completely ordered sequence. That is, each subsequence is ordered before the subsequence segments are ordered. If two ordered tables are merged into one ordered table, it is called two-way merge.
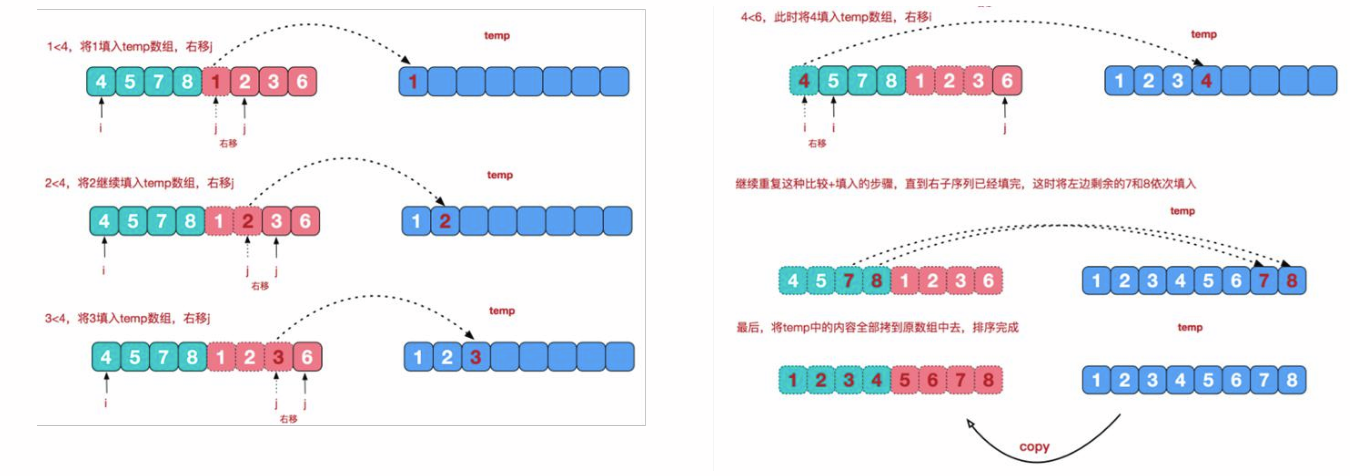
7.1 Implementation Principles
- Step 1: Request space to be the sum of two sorted sequences that will hold the merged sequence
- Step 2: Set two pointers at the beginning of two sorted sequences
- Step 3: Compare the elements that the two pointers point to, select the relatively small elements to put into the merge space, move the pointer to the next position and repeat step 3 until one pointer exceeds the end of the sequence and copy all the remaining elements of the other sequence directly to the end of the merge sequence
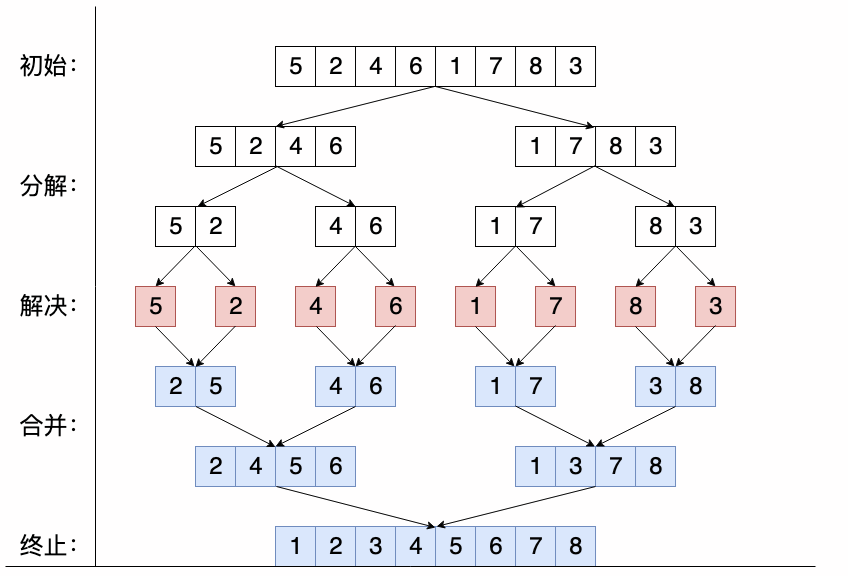
We need to merge two already ordered subsequences into one ordered sequence, such as the last merge in the figure above, and merge [2,4,5,6] and [1,3,7,8] already ordered subsequences into the final sequence [1,2,3,4,5,6,7,8]
7.2 Kinematic Demo
7.3 Example Show
1 import java.util.Arrays;
2 public class MSort {
3 public static void main(String[] args) {
4 int[] array = new int[]{15,63,97,12,235,66};
5 //Temporary Array
6 int[] temp = new int[array.length];
7 sort(array,0,array.length-1,temp);
8 System.out.println(Arrays.toString(array));
9
10 }
11 public static void sort(int[] array,int left,int right,int[] temp){
12 if (left13
14 // Find the middle value
15 int mid = (left+right)/2;
16
17 // Decomposition Left
18 sort(array,left,mid,temp);
19 // Decomposition Right
20 sort(array,mid+1,right,temp);
21 // Merge data
22 sum(array,left,right,mid,temp);
23 }
24 }
25 /**
26 * Merge Elements
27 * @param array
28 * @param left
29 * @param right
30 * @param mid
31 * @param temp
32 */
33 public static void sum(int[] array,int left,int right,int mid,int[] temp){
34 int i = left;
35 int j = mid+1;
36
37 // Point to Temporary Array Subscript
38 int t = 0;
39
40 // Start a loop to compare left and right array elements
41 while (i<=mid && j<=right){
42
43 if (array[i]<=array[j]){
44 temp[t] = array[i];
45 t++;
46 i++;
47 }else {
48 temp[t] = array[j];
49 t++;
50 j++;
51 }
52 }
53
54 // Store the remaining elements directly in a temporary array
55 while(i<=mid){
56 temp[t] = array[i];
57 t++;
58 i++;
59 }
60 while (j<=right){
61 temp[t] = array[j];
62 t++;
63 j++;
64 }
65
66 // Copy elements from temporary array to original array
67 int tempIndex = left;
68 int k = 0;
69 while (tempIndex<=right){
70 array[tempIndex] = temp[k];
71 k++;
72 tempIndex++;
73 }
74 }
75 }
Sort results display:
8. Count sorting
Count sorting is a non-comparison-based sorting algorithm proposed by Harold H. Seward in 1954. Its advantage is that when sorting a range of integers, its complexity is Ο (n+k) (where K is the range of integers) faster than any comparison sort algorithm. Of course, this is a trade-off of space for time, and when O(k)>O(nlog(n)) is less efficient than comparison-based sorting (the theoretical lower limit of time complexity for comparison-based sorting is O(nlog(n)), such as merge sorting, heap sorting)
8.1 Implementation Principles
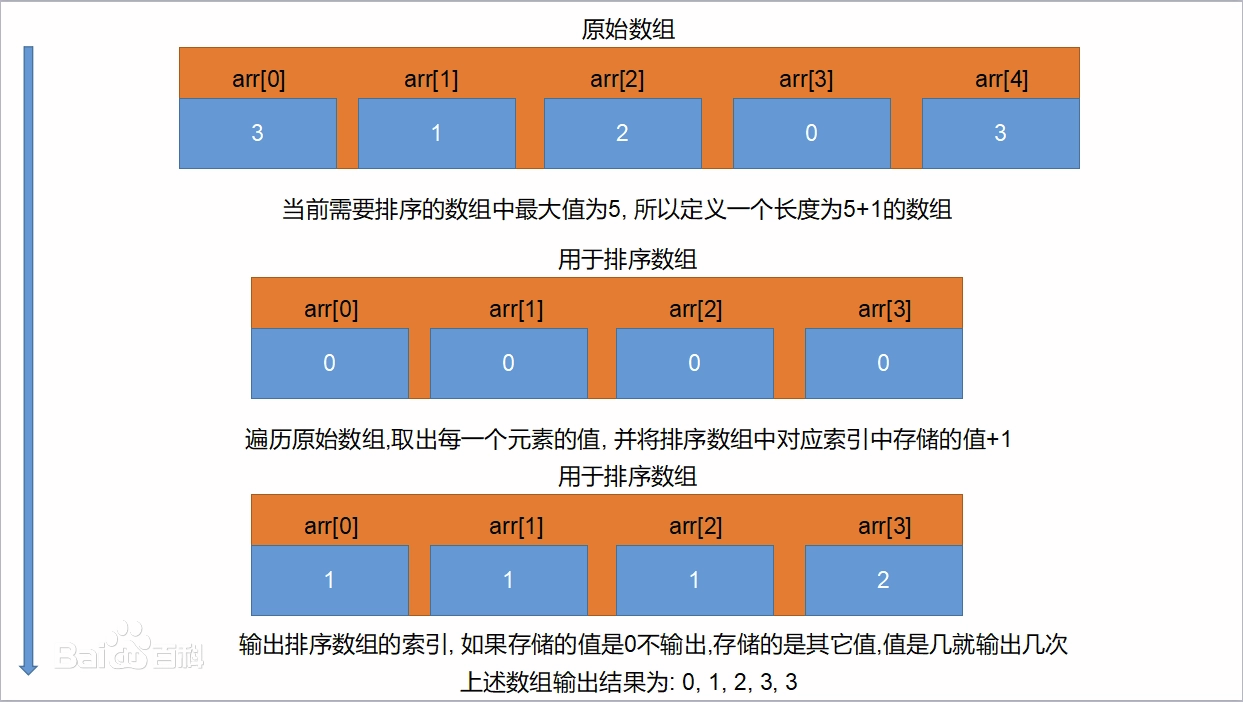
Assume that the length of the input linear table L is n, L=L1,L2,..., L n; The elements of the linear table belong to the finite partial set S, |S|=k and k=O(n), S={S1,S2,... S k}; Then the sorting of counts can be described as follows:
- Scanning the entire set S, for each Si < S, the number T(Si) of elements less than or equal to Si in linear table L is found.
- Scanning the entire linear table L, for each element Li in L, place Li at position T(Li) of the output linear table and subtract T(Li) by 1.
8.2 Kinematic Demo
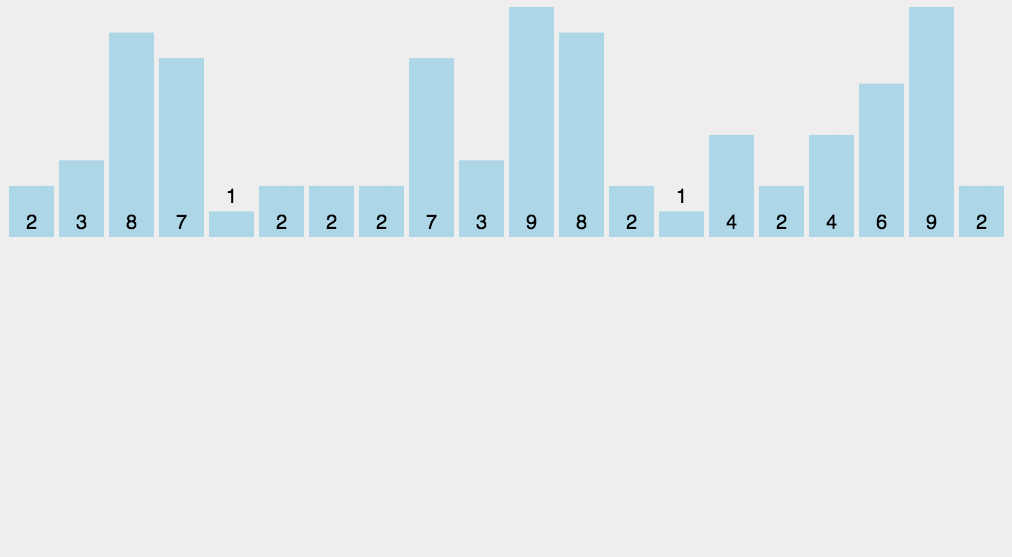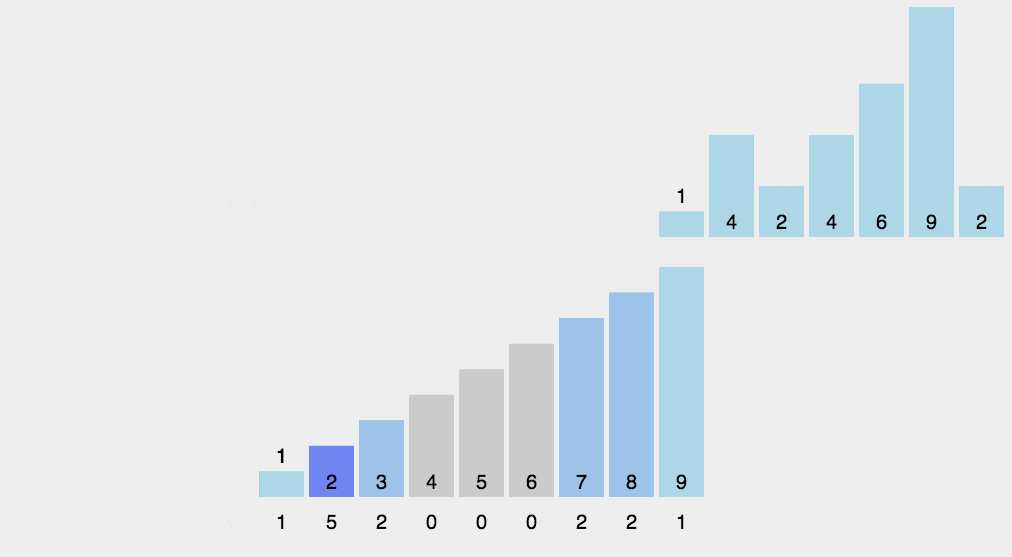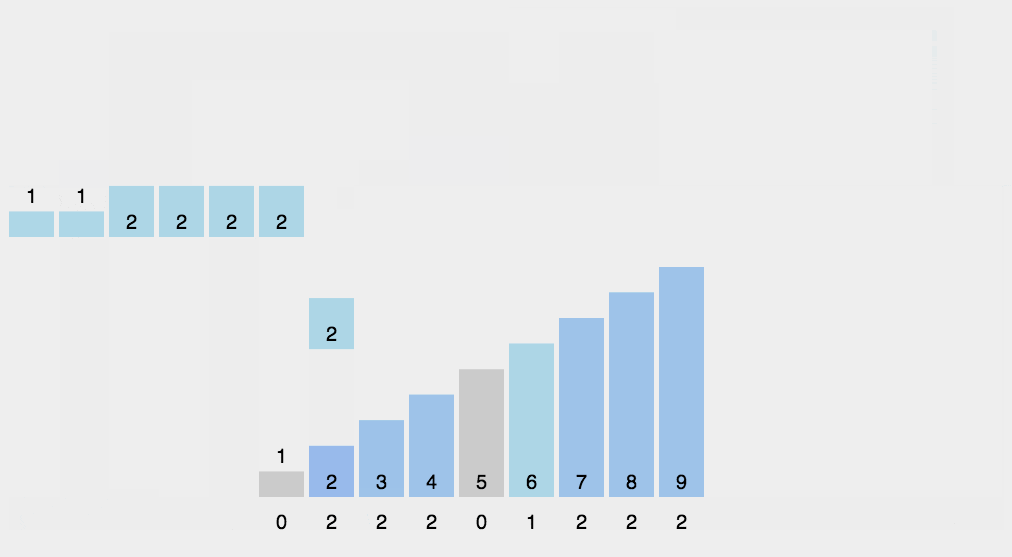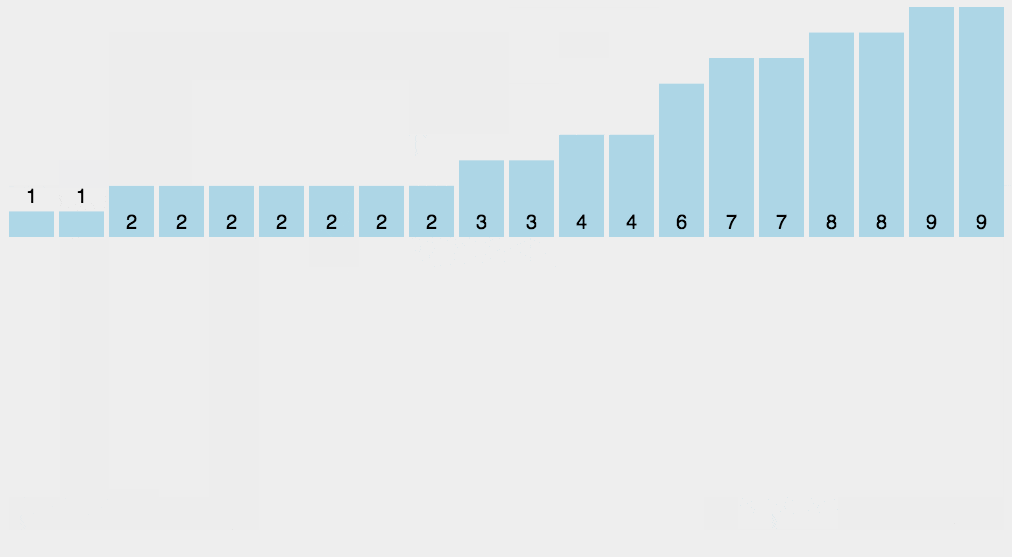
8.3 Instance Show
1 public class CountSort {
2 public static void main(String[]args){
3 //Sorted Array
4 int a[]={15,63,97,12,235,66};
5 int b[]=countSort(a);
6 for(int i:b){
7 System.out.print( i+",");
8 }
9 System.out.println();
10 }
11 public static int[] countSort(int[]a){
12 int b[] = new int[a.length];
13 int max = a[0],min = a[0];
14 for(int i:a){
15 if(i>max){
16 max=i;
17 }
18 if(i19 min=i;
20 }
21 }//Here the size of k is the extreme difference of element size + 1 in the array to be sorted
22 int k=max-min+1;
23 int c[]=new int[k];
24 for(int i=0;i25 c[a[i]-min]+=1;//Optimized to reduce the size of array c
26 }
27 for(int i=1;i28 c[i]=c[i]+c[i-1];
29 }
30 for(int i=a.length-1;i>=0;--i){
31 b[--c[a[i]-min]]=a[i];//Remove elements of c by access
32 }
33 return b;
34 }
35 }
Sort results display:
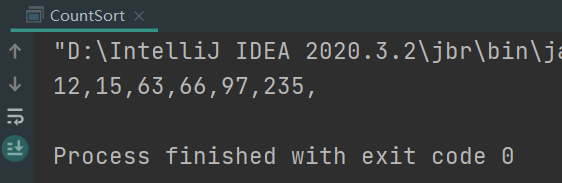
9. Heap Sorting
Heapsort is a sort algorithm designed with heap as the data structure. A heap is a nearly complete binary tree structure that also satisfies the nature of stacking: that is, the key value or index of a child node is always less than (or greater than) its parent node.
9.1 Implementation Principles
- Create a heap H[0...n-1];
- Swap the heap head (maximum) with the heap tail;
- Reduce heap size by 1 and call shift_down(0), the purpose is to adjust the top data of the new array to the corresponding position;
- Repeat step 2 until the heap size is 1.
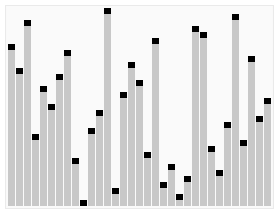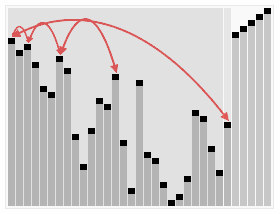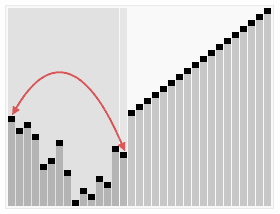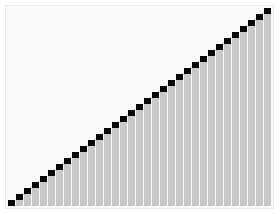
9.2 Kinematic Demo

9.3 Instance Show
1 public static int[] heapSort(int[] array) {
2 //Here the index of the element starts at 0, so the last non-leaf node array.length/2 - 1
3 for (int i = array.length / 2 - 1; i >= 0; i--) {
4 adjustHeap(array, i, array.length); //Adjust heap
5 }
6
7 // The above logic, end of build
8 // Next, start sorting logic
9 for (int j = array.length - 1; j > 0; j--) {
10 // Element exchange to remove the heap
11 // Put the root element of the big top heap at the end of the array; In other words, after each heap adjustment, one element reaches its final location
12 swap(array, 0, j);
13 // After the elements have been exchanged, there is no doubt that sorting is no longer a concern for the last element.
14 // The next thing we need to sort is that we have removed some of the elements from the heap, which is why this method is placed in the loop
15 // And here, essentially, it's top-down, left-to-right
16 adjustHeap(array, 0, j);
17 }
18 return array;
19 }
20
21 /**
22 * The most critical place to sort the entire heap
23 * @param array Standby heap
24 * @param i Start Node
25 * @param length Heap length
26 */
27 public static void adjustHeap(int[] array, int i, int length) {
28 // Remove the current element first, because it may be moving all the time
29 int temp = array[i];
30 for (int k = 2 * i + 1; k < length; k = 2 * k + 1) { //2*i+1 is the left subtree of left subtree I (since I starts from 0), 2*k+1 is the left subtree of K
31 // Let k point first to the largest of the child nodes
32 if (k + 1 < length && array[k] < array[k + 1]) { //If there is a right subtree and the right subtree is larger than the left subtree
33 k++;
34 }
35 //If a node (left and right subnodes) is found to be larger than the root node, the value is exchanged
36 if (array[k] > temp) {
37 swap(array, i, k);
38 // If the child node is replaced, then the subtree rooted on the child node will be affected, so the cycle continues to judge which tree the child node is in
39 i = k;
40 } else { //Terminate the loop without swapping
41 break;
42 }
43 }
44 }
45
46 /**
47 * Exchange Elements
48 * @param arr
49 * @param a Subscript of element
50 * @param b Subscript of element
51 */
52 public static void swap(int[] arr, int a, int b) {
53 int temp = arr[a];
54 arr[a] = arr[b];
55 arr[b] = temp;
56 }
Sort results display:

10. Bucket sorting
Bucket sort, or so-called box sort, is a sort algorithm that works by dividing arrays into a limited number of buckets. Each bucket is sorted individually (possibly using a different sorting algorithm or continuing to use bucket sorting recursively). Bucket sorting is a generalization of pigeon nest sorting. Bucket sorting uses linear time when the values in the array to be sorted are evenly distributed. Θ (n)). However, bucket sorting is not a comparative sort, and it is not affected by the lower limit of O(n log n).
10.1 Implementation Principles
Assume that the input is a real number evenly distributed across [0,1] intervals generated by a random process. The interval [0,1] is divided into n equal-sized subintervals (barrels), with each barrel size of 1/n:[0,1/n], [1/n, 2/n, 3/n),..., [k/n, (k+1)/n),... Assign n input elements to these barrels, sort the elements in the barrels, and then connect the barrel inputs of 0 < A[1...n] <1 The auxiliary array B[0...n-1] is a pointer array that points to a bucket (chain table).
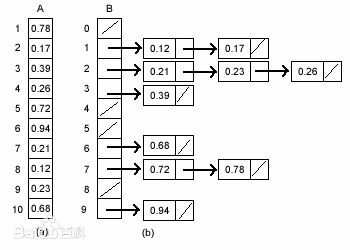
10.2 Kinematic Demo
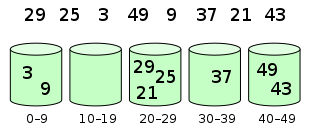
The elements are then sorted in each bucket:

10.3 Instance Show
1 public static void basket(int data[])//data is the array to be sorted
2 {
3 int n=data.length;
4 int bask[][]=new int[10][n];
5 int index[]=new int[10];
6 int max=Integer.MIN\_VALUE;
7 for(int i=0;i8 {
9 max=max>(Integer.toString(data[i]).length())?max:(Integer.toString(data[i]).length());
10 }
11 String str;
12 for(int i=max-1;i>=0;i--)
13 {
14 for(int j=0;j15 {
16 str="";
17 if(Integer.toString(data[j]).length()
18 {
19 for(int k=0;kInteger.toString(data[j]).length();k++)
20 str+="0";
21 }
22 str+=Integer.toString(data[j]);
23 bask[str.charAt(i)-'0'][index[str.charAt(i)-'0']++]=data[j];
24 }
25 int pos=0;
26 for(int j=0;j<10;j++)
27 {
28 for(int k=0;k29 {
30 data[pos++]=bask[j][k];
31 }
32 }
33 for(intx=0;x<10;x++)index[x]=0;
34 }
35 }
Sort results display:

Summary:
- That's all about the Top 10 Classic Sorting Algorithms written in this article. It's not easy to code. If it's helpful to you, leave a comment in the comments section with questions (concerns, comments, favorites).
- Please indicate the source link when reloading
Reference documents:
- 1. Baidu Encyclopedia (meaning of each noun): https://www.baidu.com/
- 2. Newbie Tutorial (Motion Map Demo): Top 10 Classic Sorting Algorithms | Rookie Birds Tutorial (runoob.com)
- 3.linux Commune: Top 10 Classic Sorting Algorithms Summary (with Java code implementation)_ Linux Programming_ Linux Commune-Linux System Portal (linuxidc.com)