General catalogue

Online evaluation address (ybt)

Evaluation address (LOJ)

Online evaluation address (LUOGU)

Understanding examples is the key.

By the middle order traversal, pre order traversal to determine the sample, binary tree form.

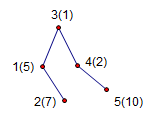
The sample score is calculated as follows:

f(2)=7
f(5)=1*7+5=12

f(5)=10
f(4)=1*10+2=12

f(3)=12*12+1=145

Node number n=5, binary tree, number of forms, the calculation process is as follows:

f(0)=1
f(1)=1

The number of nodes is 2. After deducting the root node, there is still one node left. This node is in the left subtree, corresponding to the number of forms f(1)*f(0)=1,
This node is in the right subtree, corresponding to the number of forms f(0)*f(1)=1
f(2)=f(1)*f(0)+f(0)*f(1)=2

f(3)=f(2)*f(0)+f(0)*f(2)+f(1)*f(1)=5

f(4)=f(3)*f(0)+f(0)*f(3)+f(2)*f(1)+f(1)*f(2)=5+5+2+2=14

f(5)=f(4)*f(0)+f(0)*f(4)+f(3)*f(1)+f(1)*f(3)+f(2)*f(2)=14+14+5+5+4=42

n=5, the number of forms is 42, P(5,5)=5*4*3*2*1=120 is placed at the corresponding node of each form, and the total possibility is 120 * 42 = 5040, so n=30 enumerates the problem, and it must timeout.

It is basically confirmed that the shape of the final tree is close to symmetry with respect to the root node.

The approximate algorithm is as follows:

Sort the node scores from small to large, put the root node to the minimum, put the second layer from left to right, put the second small, the third small, the third layer, from right to left, put the fourth small, the fifth small, the fourth layer, from left to right, put the sixth small, the seventh small, and so on. But it doesn't feel easy to operate.

Think again.

First of all, what we need to do is to design the state. In fact, it is to design the meaning of dp array, which should meet the requirement of no aftereffect.
Pay attention to this # left subtree * right subtree + root # I just need to know the score of left subtree and right subtree and the score of root (given), isn't it OK? No matter what his sub tree looks like!
So, what we store in ff array is the maximum score. How to store it?
We find that a subtree is a collection of one or more nodes.
So can we open a f[i][j] to represent the maximum bonus of the tree from node i to node j? You can keep this idea first (after all, you can't think of a better one for the time being).

If so, let's design the state transition equation.
According to the design just now, our answer is f[1][n], so we can start with a small subtree, that is, len, interval length. With the interval length, we need to enumerate the starting point of the interval, i is the starting point of the interval, and then we can calculate the end point j of the interval. Obviously, interval dynamic gauge.
Through the formula of the binary tree, we can know that the division of the binary tree depends on who is the root, so we enumerate the root k in the interval.
In particular, f[i][i]=a[i], where a[i] is the score of the ith node.
Because the maximum value is required, we can design it

f[i][j]=MAX(f[i][k-1]*f[k+1][j]+f[k][k])

Please note: f[i][k-1] left subtree, k-root and f[k+1][j] right subtree correspond to the middle order traversal given in the question.

Therefore, we designed a dp process by ourselves. Because it comes along, it rarely fails.

As for the output preorder traversal, we design a state root[i][j] to represent the root node selected for the maximum bonus of the tree from node i to node j.
So we can output recursively in the order of root - > left - > right.

The process simulation of sample maximum value is as follows:

f[1][1]=5,f[2][2]=7,f[3][3]=1,f[4][4]=2,f[5][5]=10
f[1][0]=1,f[2][1]=1,f[3][2]=1,f[4][3]=1,f[5][4]=1

len=1
 Take node 1 as the root node f[1][2]=max(f[1][2],f[1][0]*f[2][2]+f[1][1])=12
 Take node 2 as the root node f[1][2]=max(f[1][2],f[1][1]*f[3][2]+f[2][2])=12


Take node 2 as the root node f[2][3]=max(f[2][3],f[2][1]*f[3][3]+f[2][2])=8
 Take node 3 as the root node f[2][3]=max(f[2][3],f[1][1]*f[3][2]+f[2][2])=12

......

ybt

adopt

Test point	result	Memory	time
Test point 1	The answer is correct	620KB	2MS
Test point 2	The answer is correct	632KB	2MS
Test point 3	The answer is correct	628KB	1MS
Test point 4	The answer is correct	616KB	1MS
Test point 5	The answer is correct	640KB	1MS

LOJ

LUOGU

 

The AC code is as follows:

#include <bits/stdc++.h>
#define LL long long
#define maxn 35
using namespace std;
LL f[maxn][maxn];
int root[maxn][maxn];
void PreOrder(int lt,int rt){
	if(lt>rt)return;
	printf("%d ",root[lt][rt]);
	PreOrder(lt,root[lt][rt]-1);
	PreOrder(root[lt][rt]+1,rt);
}
int main(){
	int n,lt,rt,len,k,i;
	scanf("%d",&n);
	for(i=1;i<=n;i++)scanf("%lld",&f[i][i]);
	for(i=1;i<=n+1;i++)f[i][i-1]=1;//Vacancy tree 
	for(i=1;i<=n;i++)root[i][i]=i;
	for(len=1;len<n;len++)
		for(lt=1;lt<n;lt++){
			rt=lt+len;
			if(rt>n)break;
			for(k=lt;k<=rt;k++)//Take k as the root node 
				if(f[lt][rt]<f[lt][k-1]*f[k+1][rt]+f[k][k]){
					f[lt][rt]=f[lt][k-1]*f[k+1][rt]+f[k][k];
					root[lt][rt]=k;
				}
		}
	printf("%lld\n",f[1][n]);
	PreOrder(1,n);
	printf("\n");		
	return 0;
}