Continuous learning & continuous updating
Learning attitude: down to earth
The traditional adjacency matrix or adjacency table is not used in the code implementation diagram, because they are too complex and troublesome.
The code implementation adopts a compromise scheme, which is more inclined to the adjacency table.
When the code implements a graph, it is generally implemented as a directed graph, because an undirected graph can be expressed by a directed graph.
Implementation scheme of graph

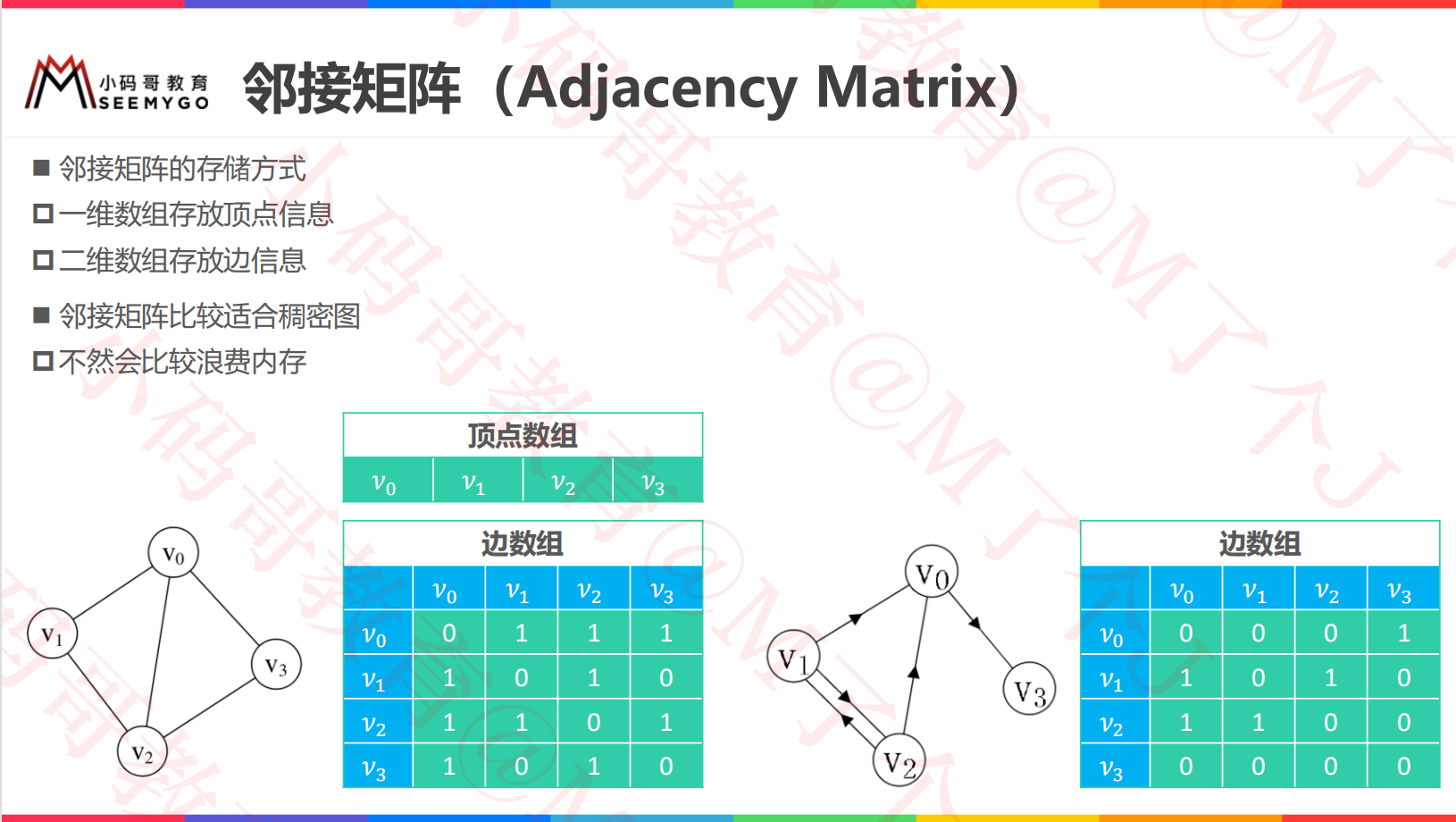
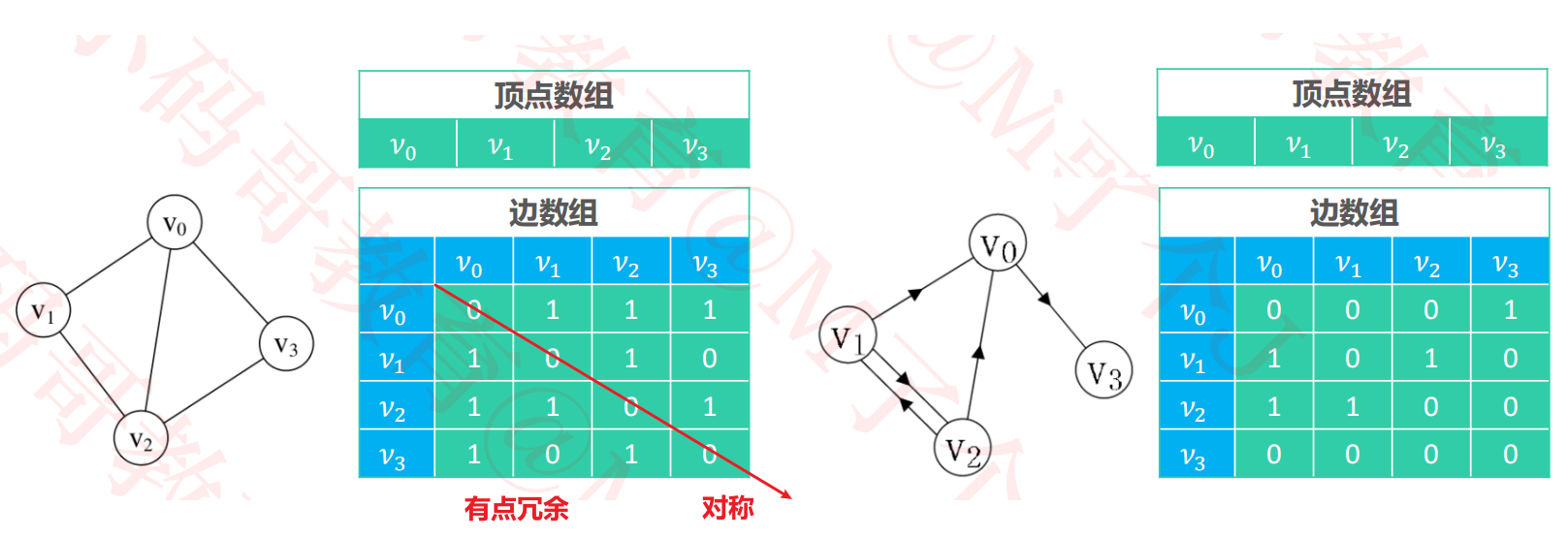
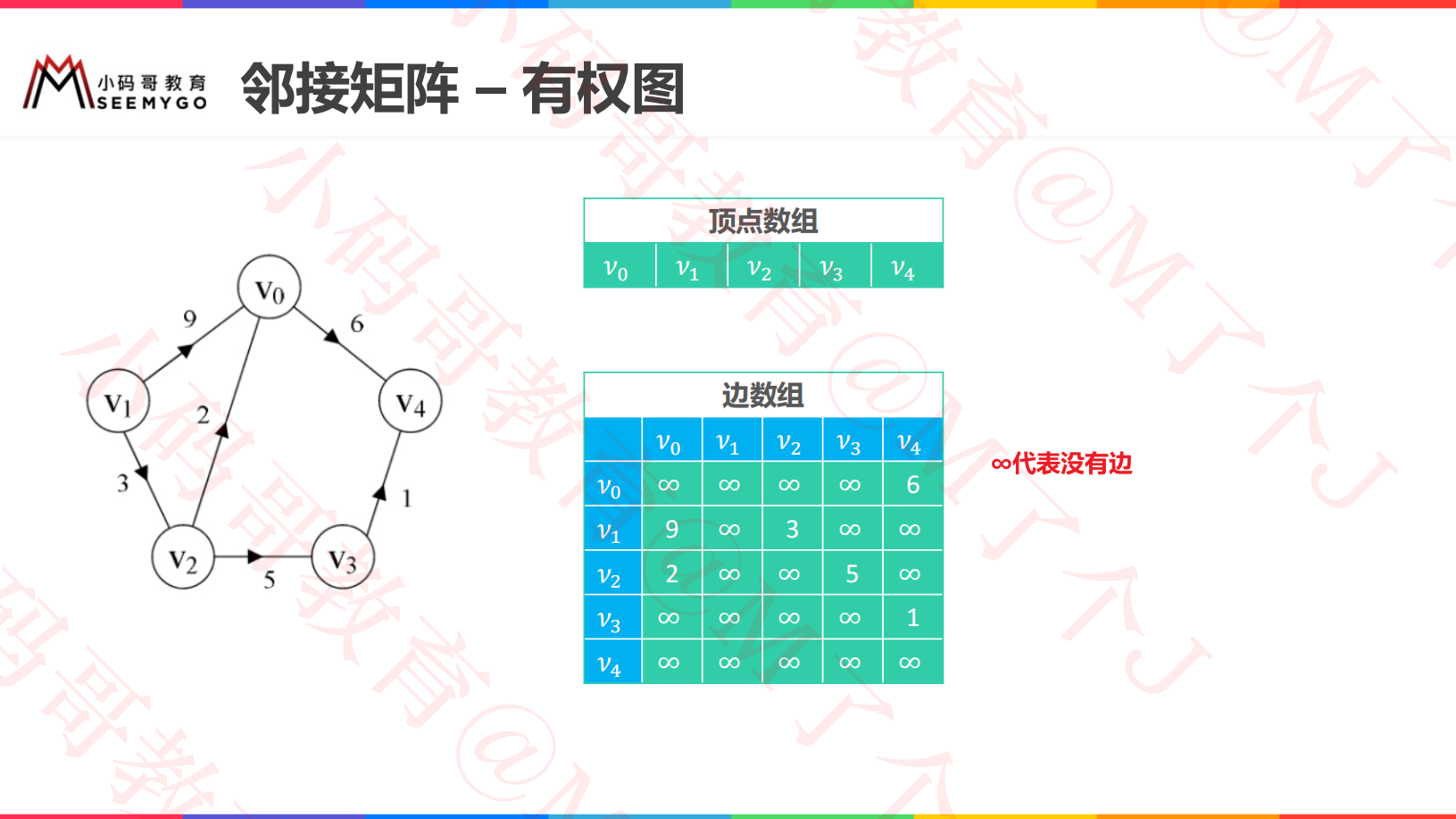
adjacency matrix
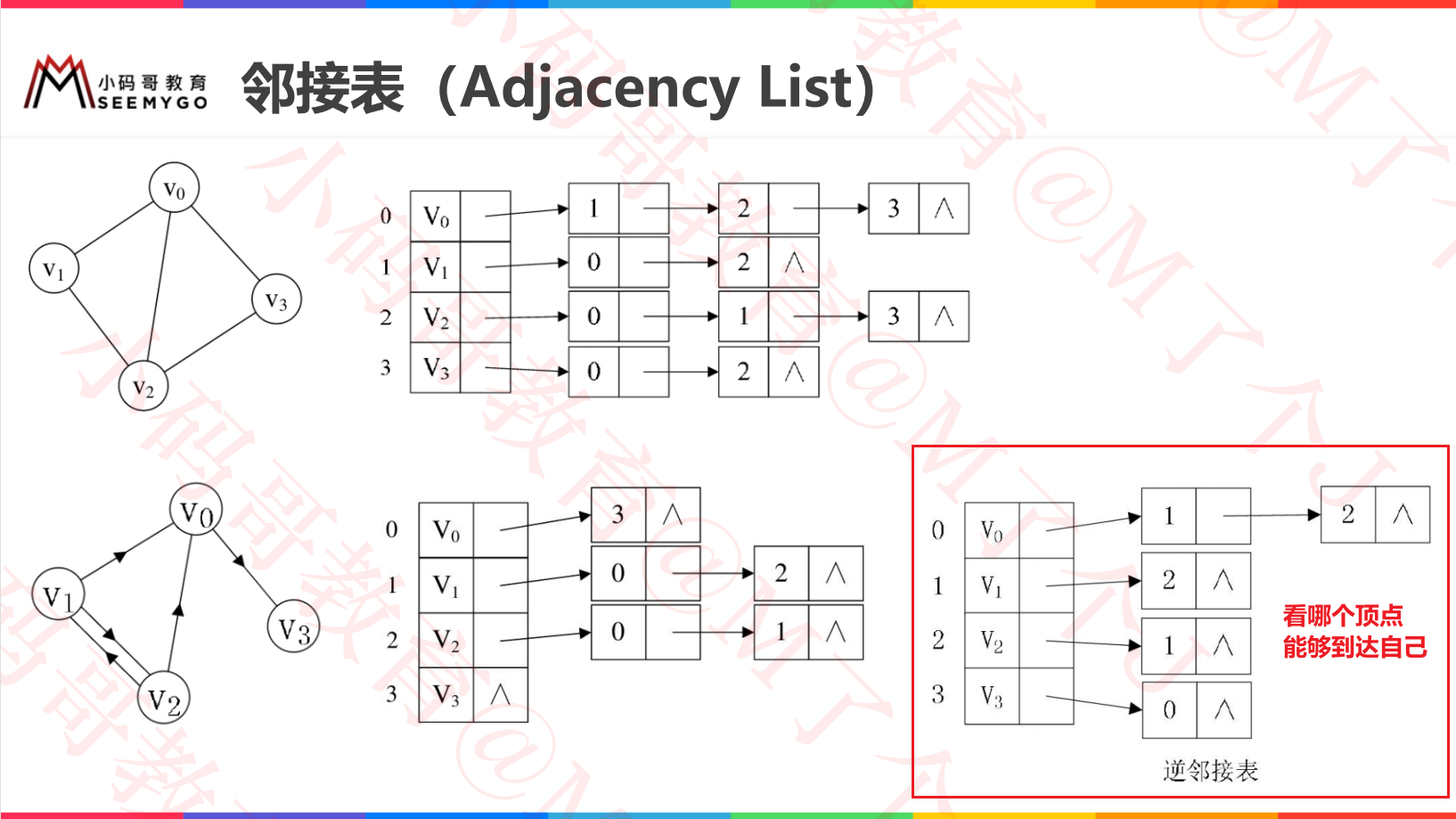
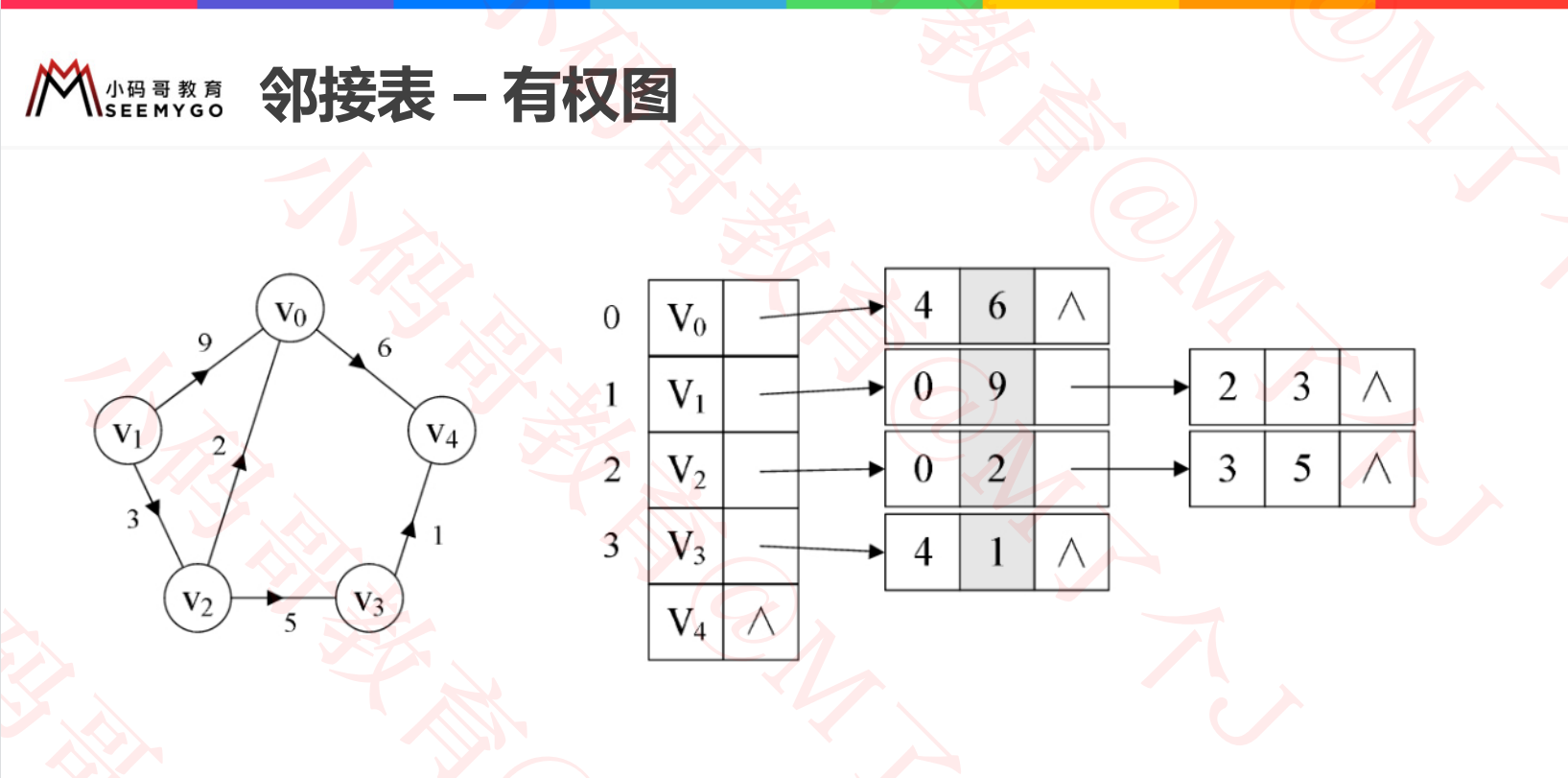
Adjacency table
The adjacency table only needs a one-dimensional array
Basic interface of figure

public interface Graph<V, E> {
int vertexSize(); // Number of vertices
int edgeSize(); // Number of edges
void addVertex(V v); // Add a vertex
void removeVertex(V v); // Delete a vertex
void addEdge(V from, V to); // Add an edge
void addEdge(V from, V to, E weight); // Add an edge (weighted)
void removeEdge(V from, V to); // Delete an edge
}
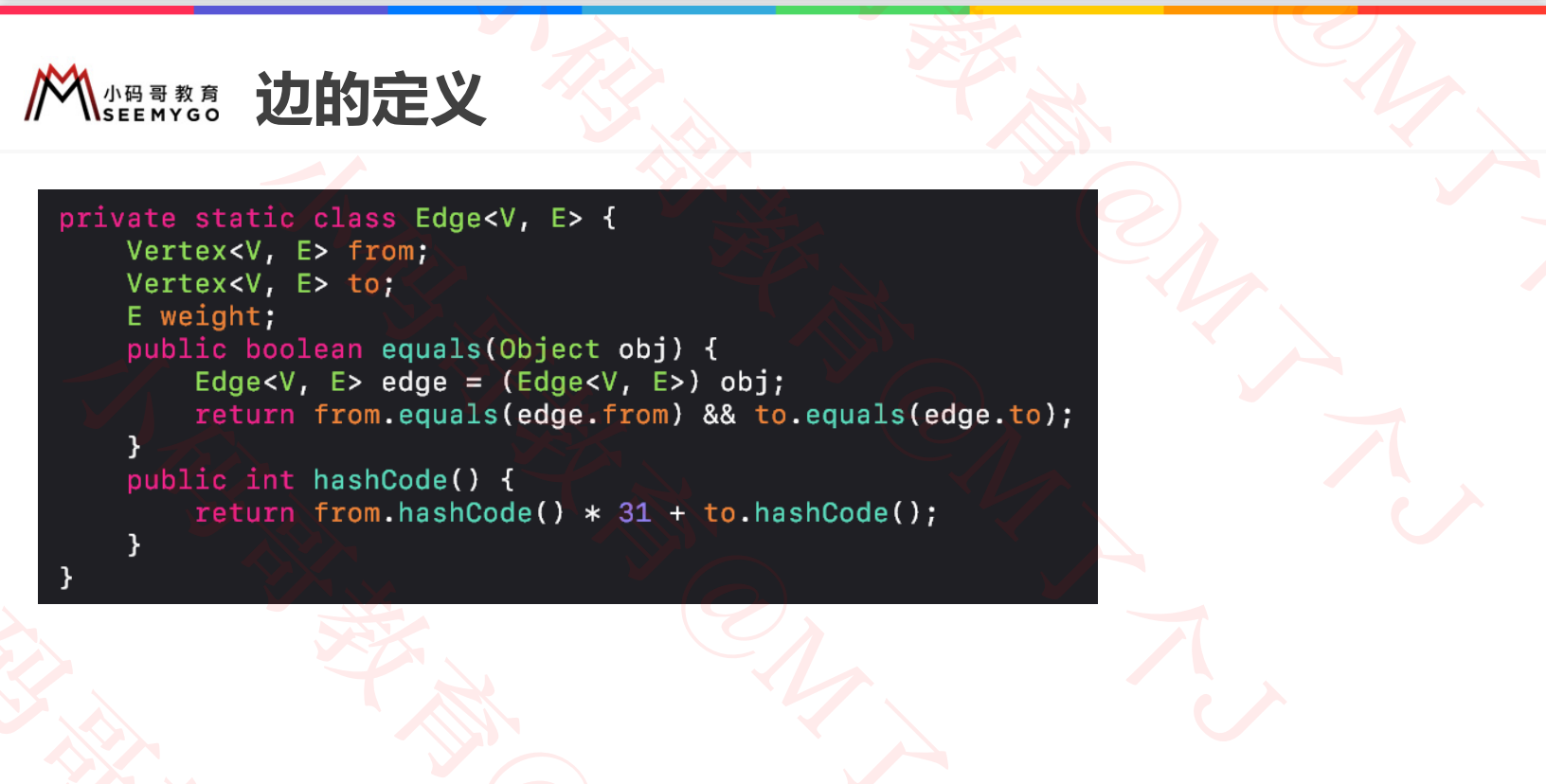
Definition of vertex and edge

public class ListGraph<V, E> implements Graph<V, E> {
// vertex
private static class Vertex<V, E> {
V value; // Vertex stored elements
Set<Edge<V, E>> inEdges = new HashSet<>(); // The edge that ends at the vertex (the edge that reaches the vertex)
Set<Edge<V, E>> outEdges = new HashSet<>(); // Edge starting from this vertex (edge starting from this vertex)
Vertex(V value) {
this.value = value;
}
@Override
public boolean equals(Object o) {
Vertex<V, E> vertex = (Vertex<V, E>) o;
return Objects.equals(value, vertex.value);
}
@Override
public int hashCode() {
return value != null ? value.hashCode() : 0;
}
@Override
public String toString() {
return value == null ? "null" : value.toString();
}
}
// edge
private static class Edge<V, E> {
E weight; // Weight of edge
Vertex<V, E> from; // Which vertex does this edge start from
Vertex<V, E> to; // Which vertex does this edge reach
Edge(Vertex<V, E> from, Vertex<V, E> to, E weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public boolean equals(Object o) {
Edge<V, E> edge = (Edge<V, E>) o;
return from.equals(edge.from) && to.equals(edge.to);
}
@Override
public int hashCode() {
int result = 0;
result = 31 * result + from.hashCode();
result = 31 * result + to.hashCode();
return result;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
}
Basic implementation of graph
public class ListGraph<V, E> implements Graph<V, E> {
private final Map<V, Vertex<V, E>> vertices = new HashMap<>();
private final Set<Edge<V, E>> edges = new HashSet<>();
public void print() {
System.out.println("Vertex:");
vertices.forEach((k, v) -> {
System.out.println(k);
System.out.println("in:");
System.out.println(v.inEdges);
System.out.println("out:");
System.out.println(v.outEdges);
System.out.println("---------------------");
});
System.out.println("Edge:");
edges.forEach(System.out::println);
}
@Override
public int vertexSize() {
return vertices.size();
}
@Override
public int edgeSize() {
return edges.size();
}
@Override
public void addVertex(V v) {
if (vertices.containsKey(v)) return;
vertices.put(v, new Vertex<>(v));
}
@Override
public void removeVertex(V v) {
// Vertex<V, E> vertex = vertices.get(v);
// if (null == vertex) return;
final Vertex<V, E> removeVertex = vertices.remove(v);
if (null == removeVertex) return;
for (Iterator<Edge<V, E>> iterator = removeVertex.outEdges.iterator(); iterator.hasNext(); ) {
final Edge<V, E> edge = iterator.next();
edges.remove(edge);
edge.to.inEdges.remove(edge);
// iterator.remove();
}
// removeVertex.outEdges.clear();
removeVertex.outEdges = null;
for (Iterator<Edge<V, E>> iterator = removeVertex.inEdges.iterator(); iterator.hasNext(); ) {
final Edge<V, E> edge = iterator.next();
edges.remove(edge);
edge.from.outEdges.remove(edge);
// iterator.remove();
}
// removeVertex.inEdges.clear();
removeVertex.inEdges = null;
}
@Override
public void addEdge(V from, V to) {
addEdge(from, to, null);
}
// If you find that a vertex does not exist, you need to create it
@Override
public void addEdge(V from, V to, E weight) {
Vertex<V, E> fromVertex = vertices.get(from);
Vertex<V, E> toVertex = vertices.get(to);
if (fromVertex == null) {
fromVertex = new Vertex<>(from);
vertices.put(from, fromVertex);
}
if (toVertex == null) {
toVertex = new Vertex<>(to);
vertices.put(to, toVertex);
}
Edge<V, E> edge = new Edge<>(fromVertex, toVertex, weight);
if (fromVertex.outEdges.remove(edge)) { // If this edge already exists
toVertex.inEdges.remove(edge);
edges.remove(edge);
}
fromVertex.outEdges.add(edge);
toVertex.inEdges.add(edge);
edges.add(edge);
}
@Override
public void removeEdge(V from, V to) {
Vertex<V, E> fromVertex = vertices.get(from);
Vertex<V, E> toVertex = vertices.get(to);
if (fromVertex == null || toVertex == null) {
return;
}
Edge<V, E> edge = new Edge<>(fromVertex, toVertex, null);
if (edges.remove(edge)) { // If this edge exists, it needs to be deleted
toVertex.inEdges.remove(edge);
fromVertex.outEdges.remove(edge);
}
}
// vertex
private static class Vertex<V, E> {
V value; // Vertex stored elements
Set<Edge<V, E>> inEdges = new HashSet<>(); // The edge that ends at the vertex (the edge that reaches the vertex)
Set<Edge<V, E>> outEdges = new HashSet<>(); // Edge starting from this vertex (edge starting from this vertex)
Vertex(V value) {
this.value = value;
}
@Override
public boolean equals(Object o) {
Vertex<V, E> vertex = (Vertex<V, E>) o;
return Objects.equals(value, vertex.value);
}
@Override
public int hashCode() {
return value != null ? value.hashCode() : 0;
}
@Override
public String toString() {
return value == null ? "null" : value.toString();
}
}
// edge
private static class Edge<V, E> {
E weight; // Weight of edge
Vertex<V, E> from; // Which vertex does this edge start from
Vertex<V, E> to; // Which vertex does this edge reach
Edge(Vertex<V, E> from, Vertex<V, E> to, E weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public boolean equals(Object o) {
Edge<V, E> edge = (Edge<V, E>) o;
return from.equals(edge.from) && to.equals(edge.to);
}
@Override
public int hashCode() {
int result = 0;
result = 31 * result + from.hashCode();
result = 31 * result + to.hashCode();
return result;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
}
Traversal of Graphs
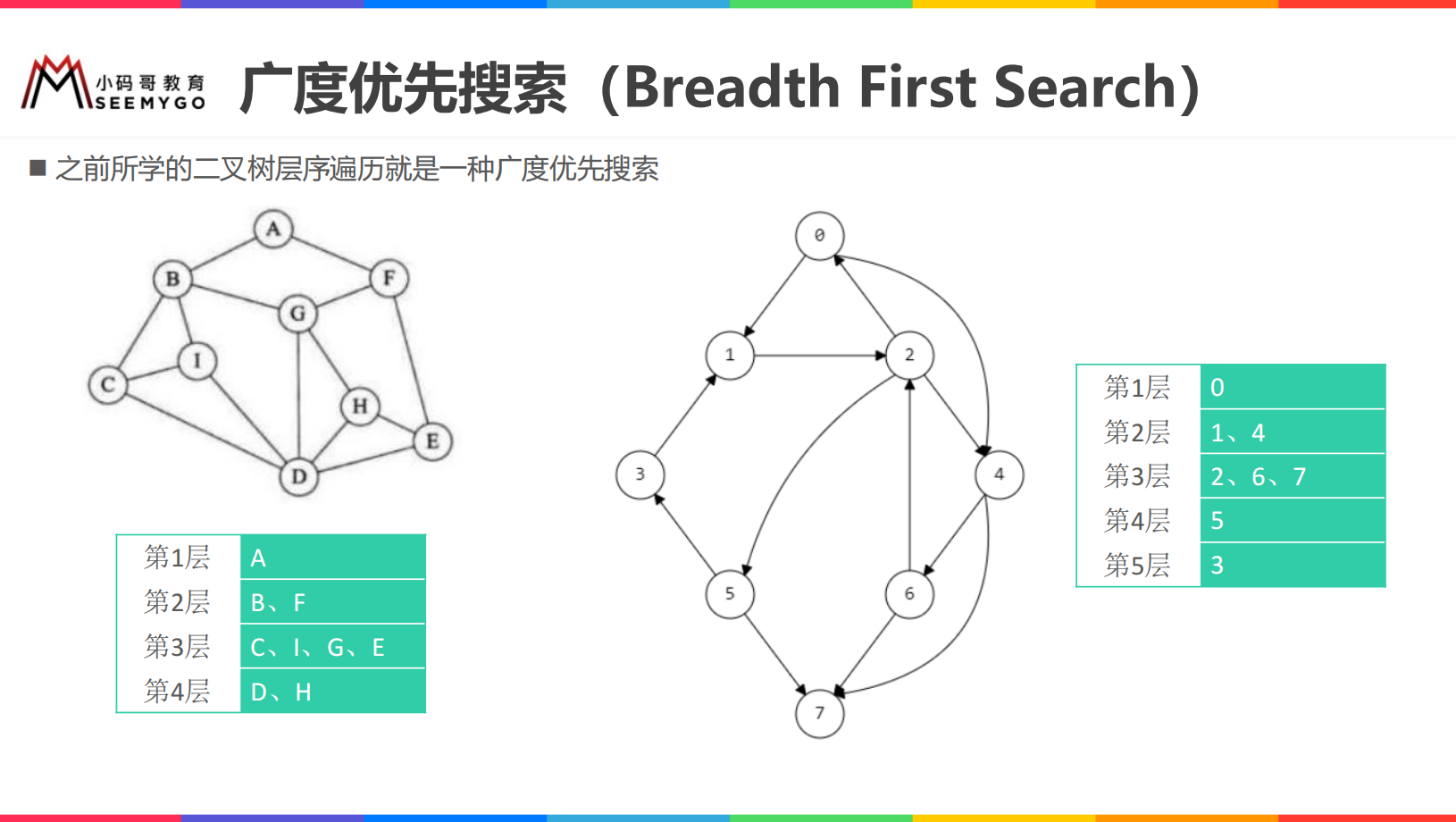
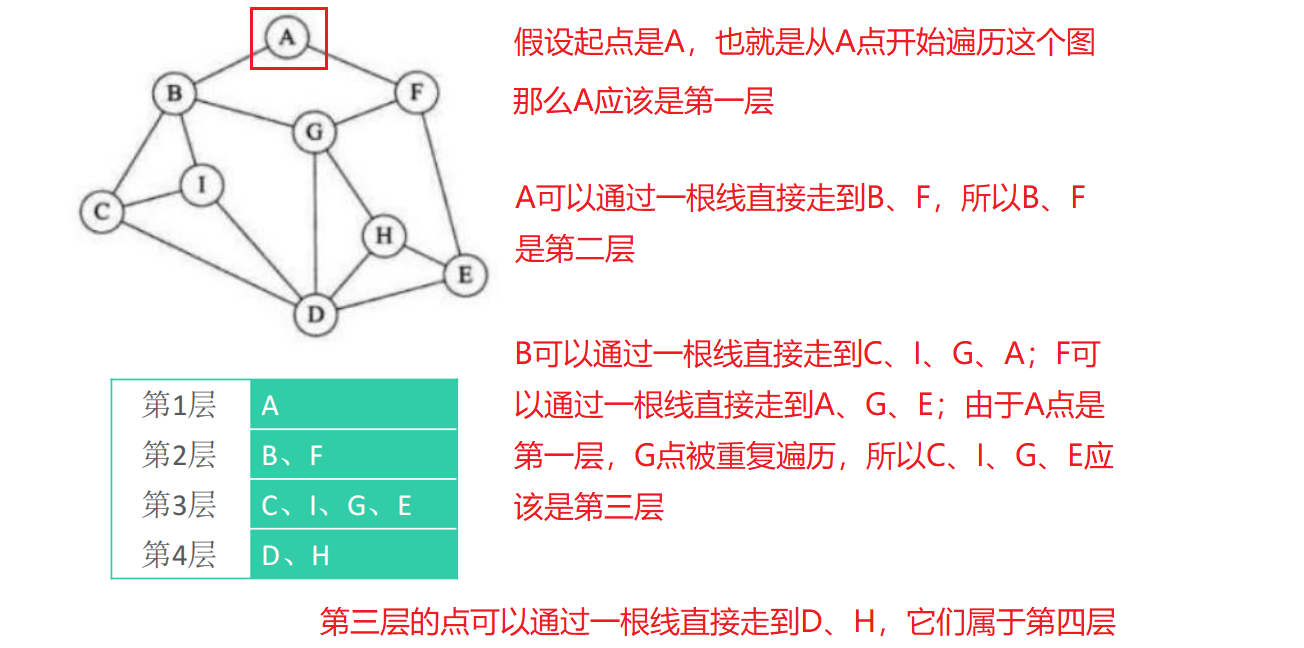
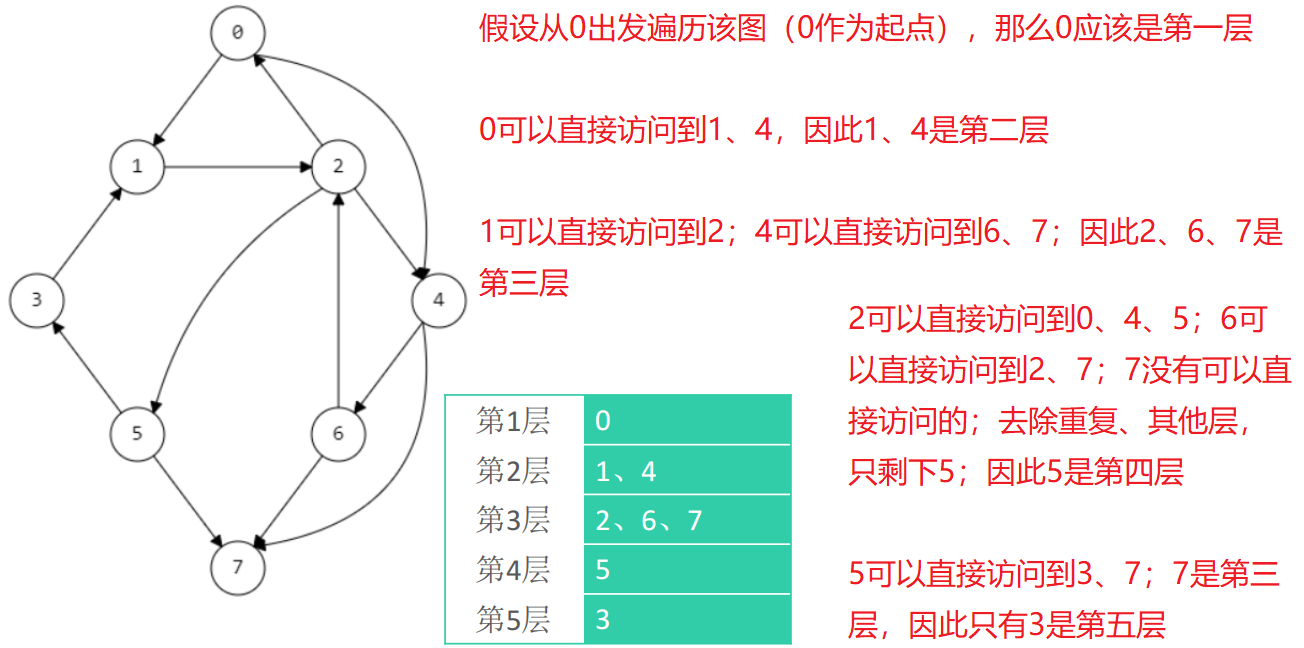
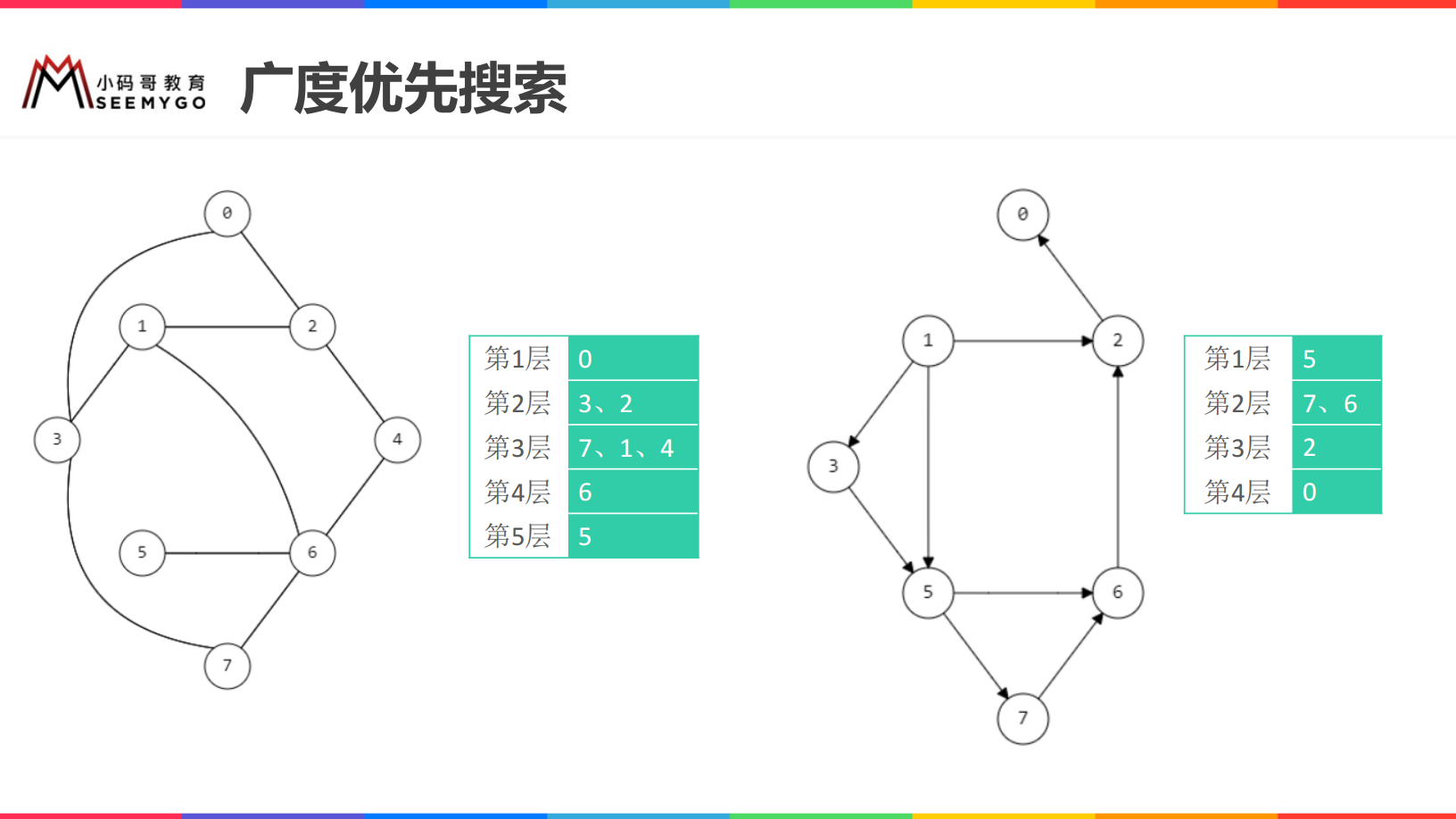
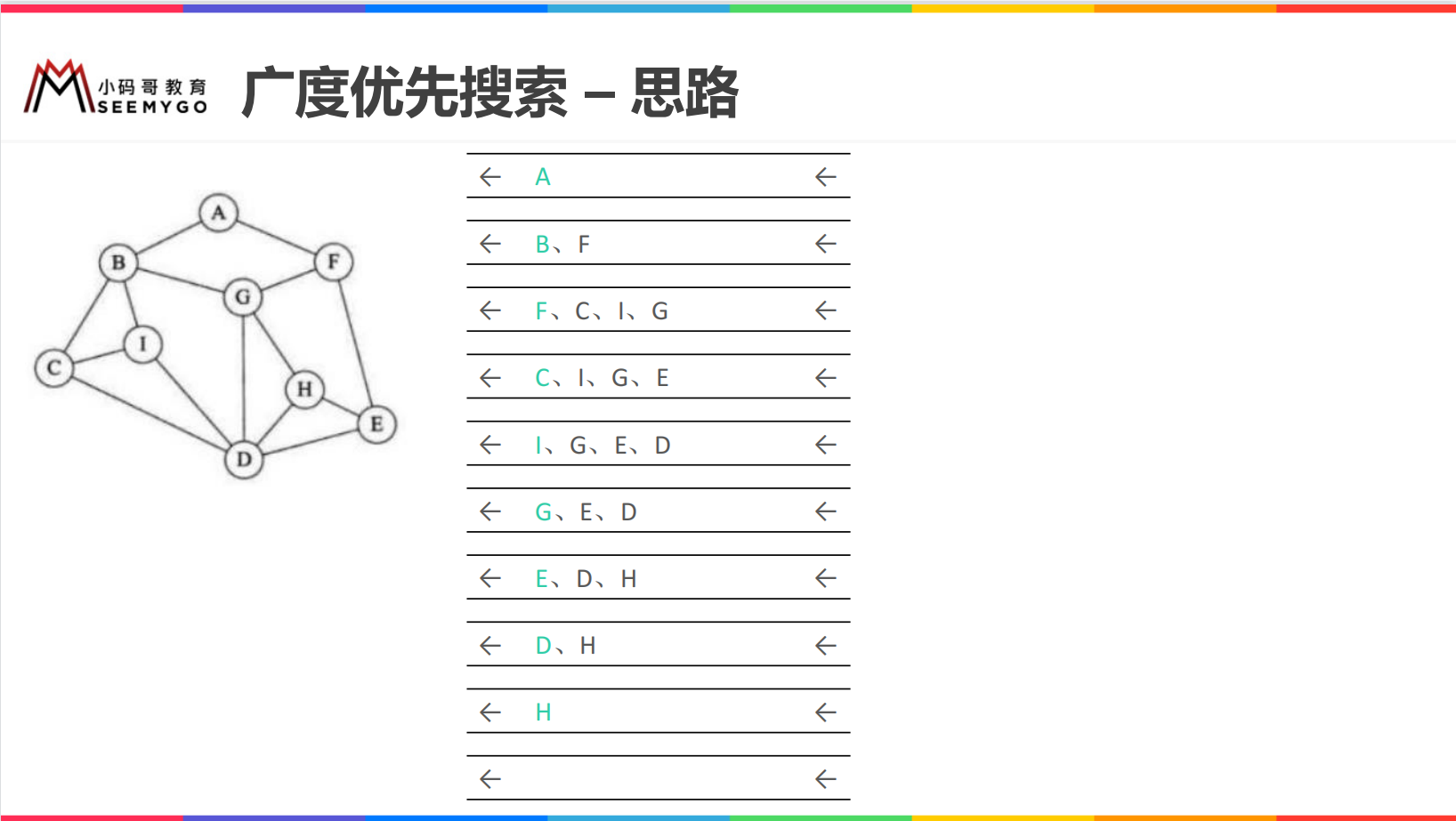
Breadth first search
When using breadth first search to traverse a graph, the traversal results are different from different vertices (it should be noted that some vertices can not be traversed sometimes)
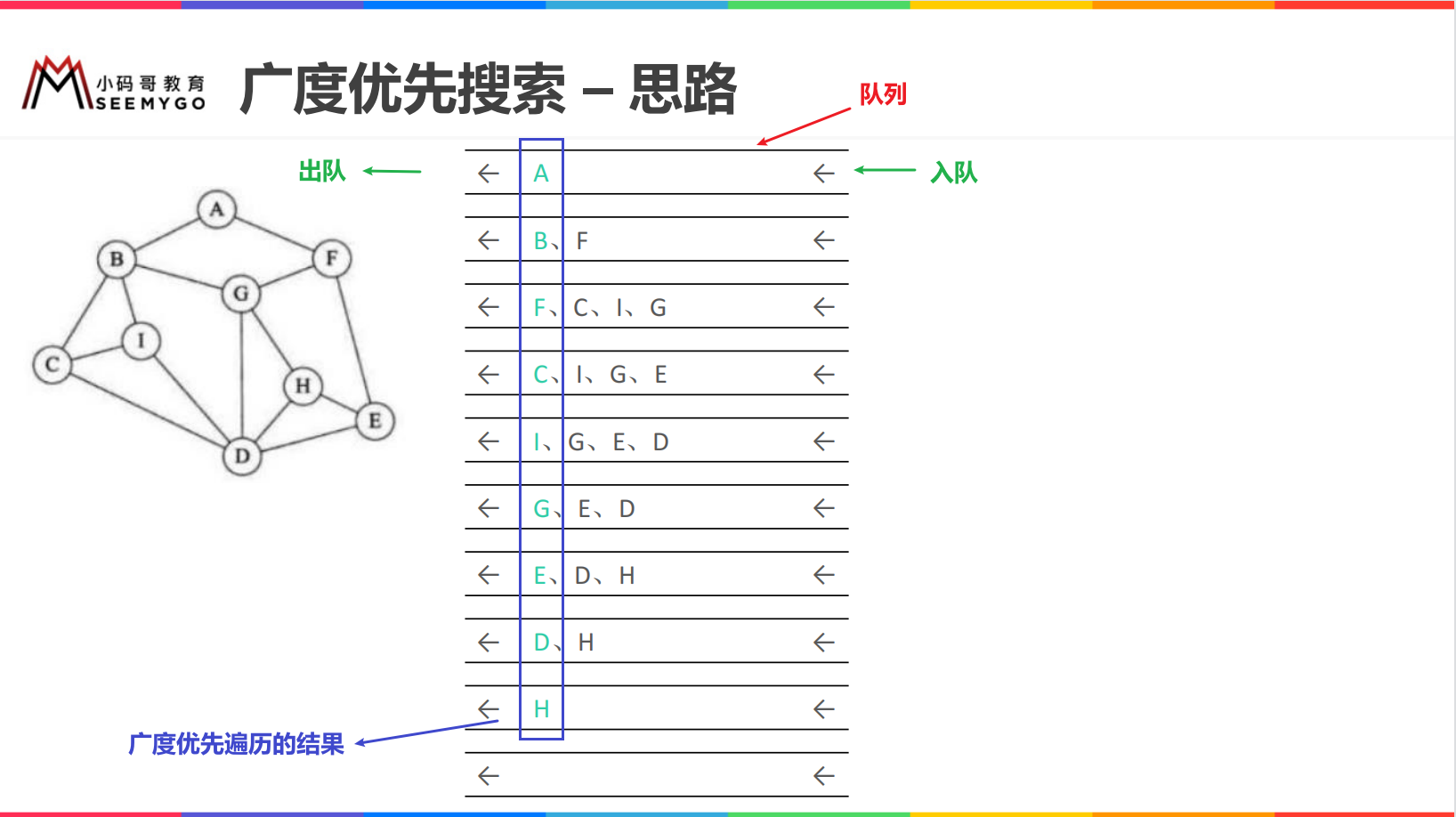
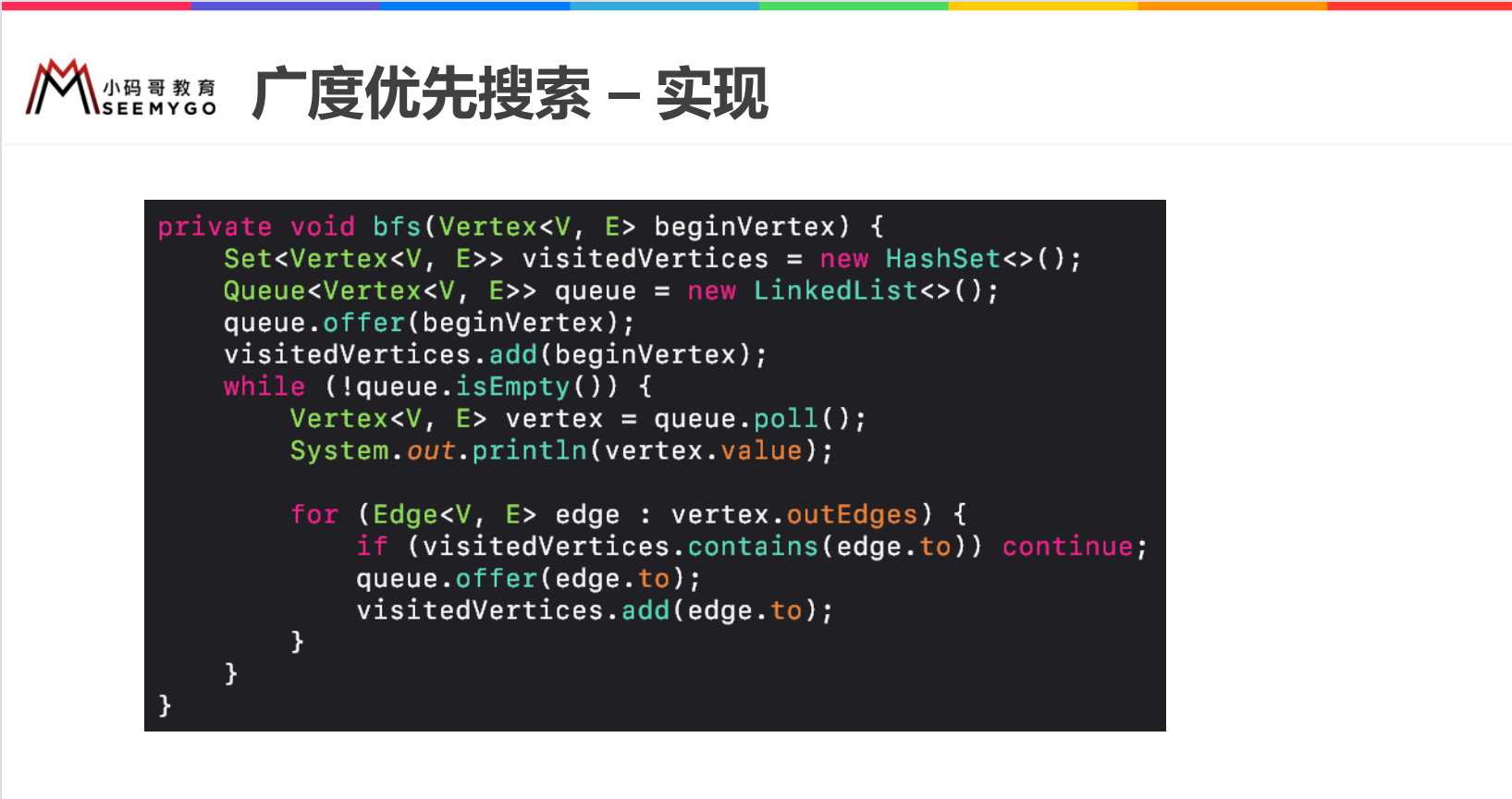
// Breadth first search
@Override
public void bfs(V begin) {
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Queue<Vertex<V, E>> queue = new LinkedList<>();
Set<Vertex<V, E>> set = new HashSet<>();
queue.offer(beginVertex);
set.add(beginVertex);
while (!queue.isEmpty()) {
final Vertex<V, E> vertex = queue.poll();
System.out.println(vertex); // The traversal here is simply to print the vertices
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
queue.offer(edge.to);
set.add(edge.to);
}
}
}
Depth first search
When using the depth first search to traverse the graph, starting from different vertices, the traversal results will be different as the breadth first search (it should be noted that some vertices can not be traversed sometimes);
When using depth first search to traverse the graph, there will be many paths to traverse from the same vertex.
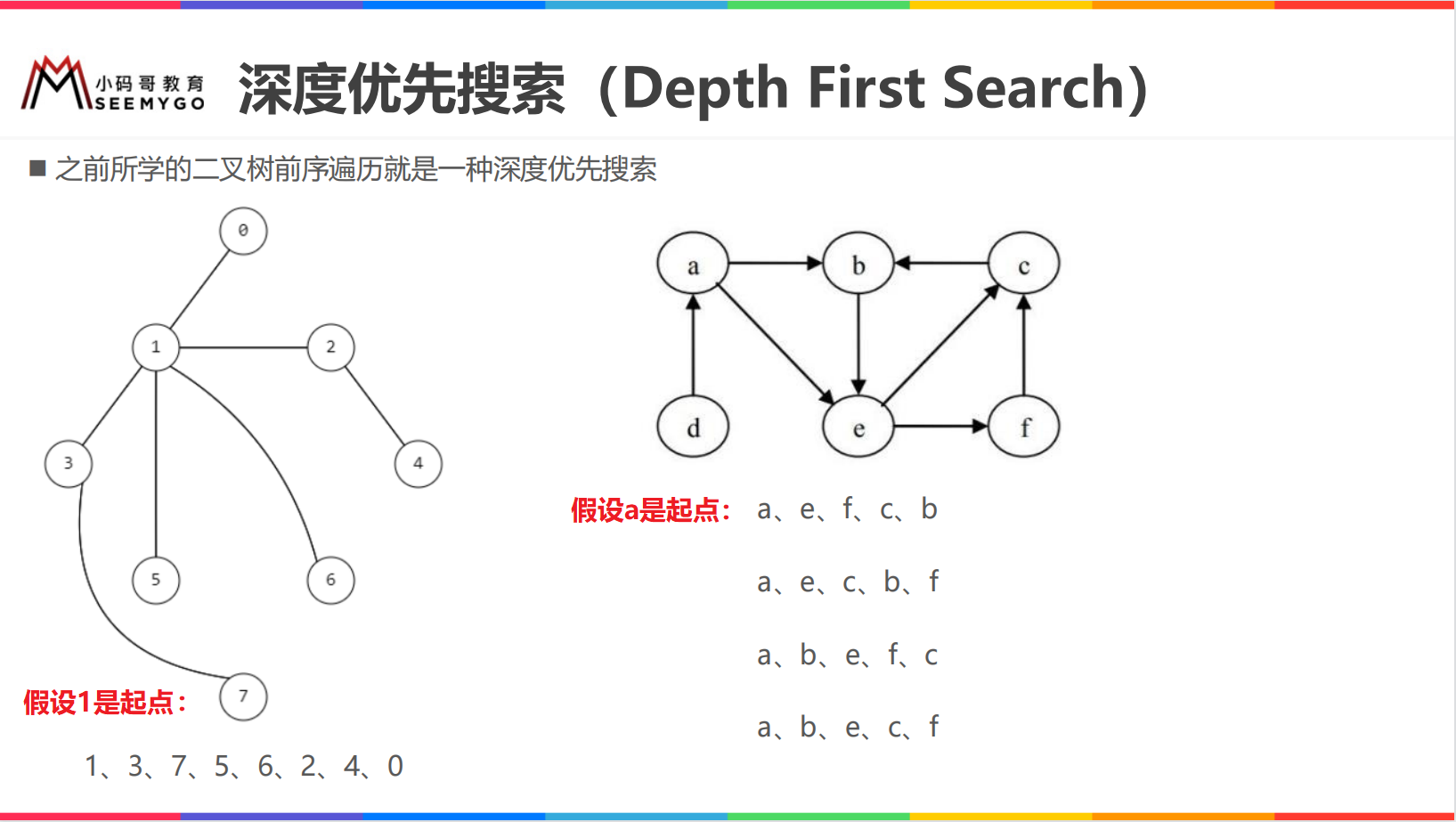
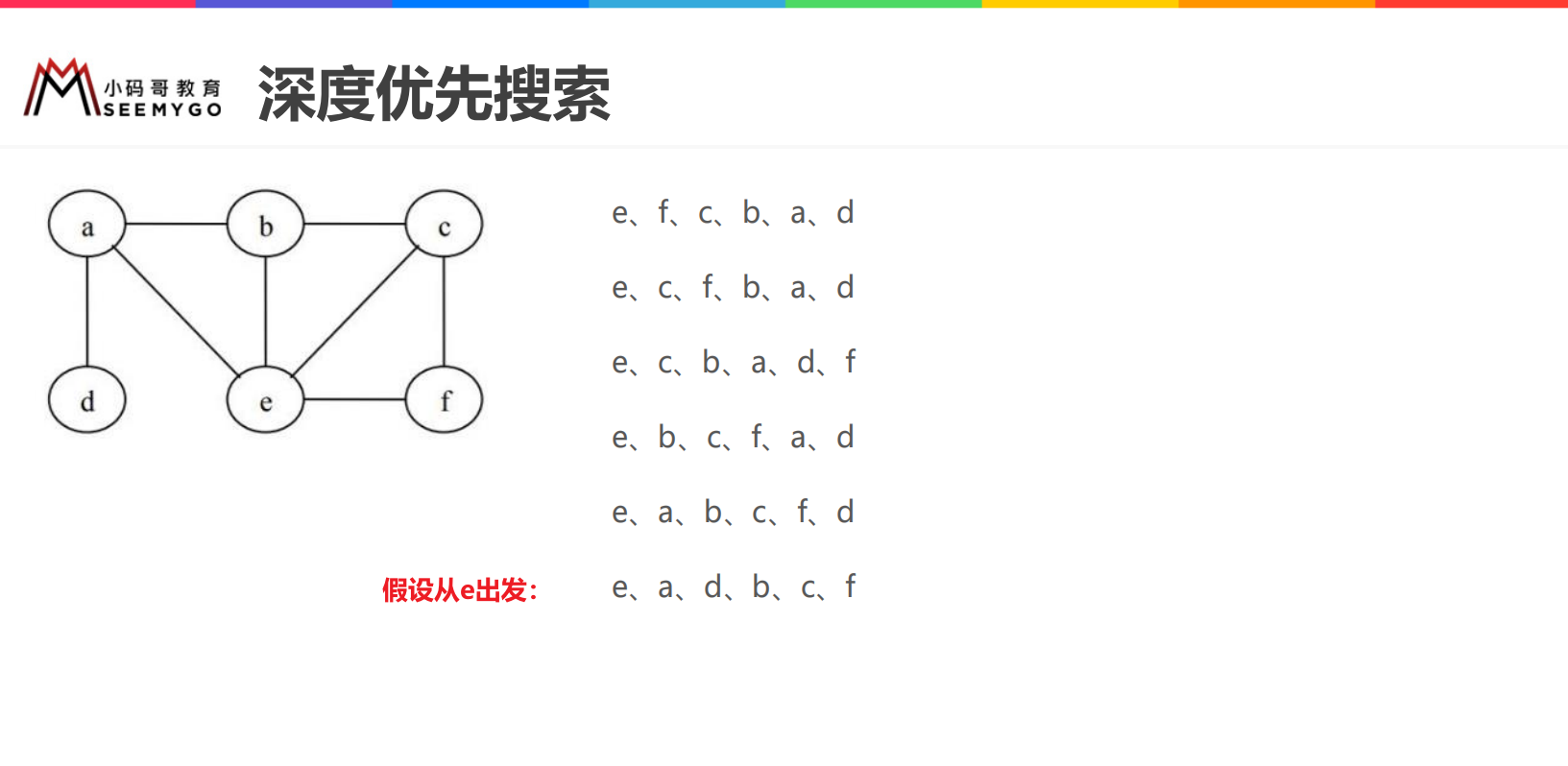

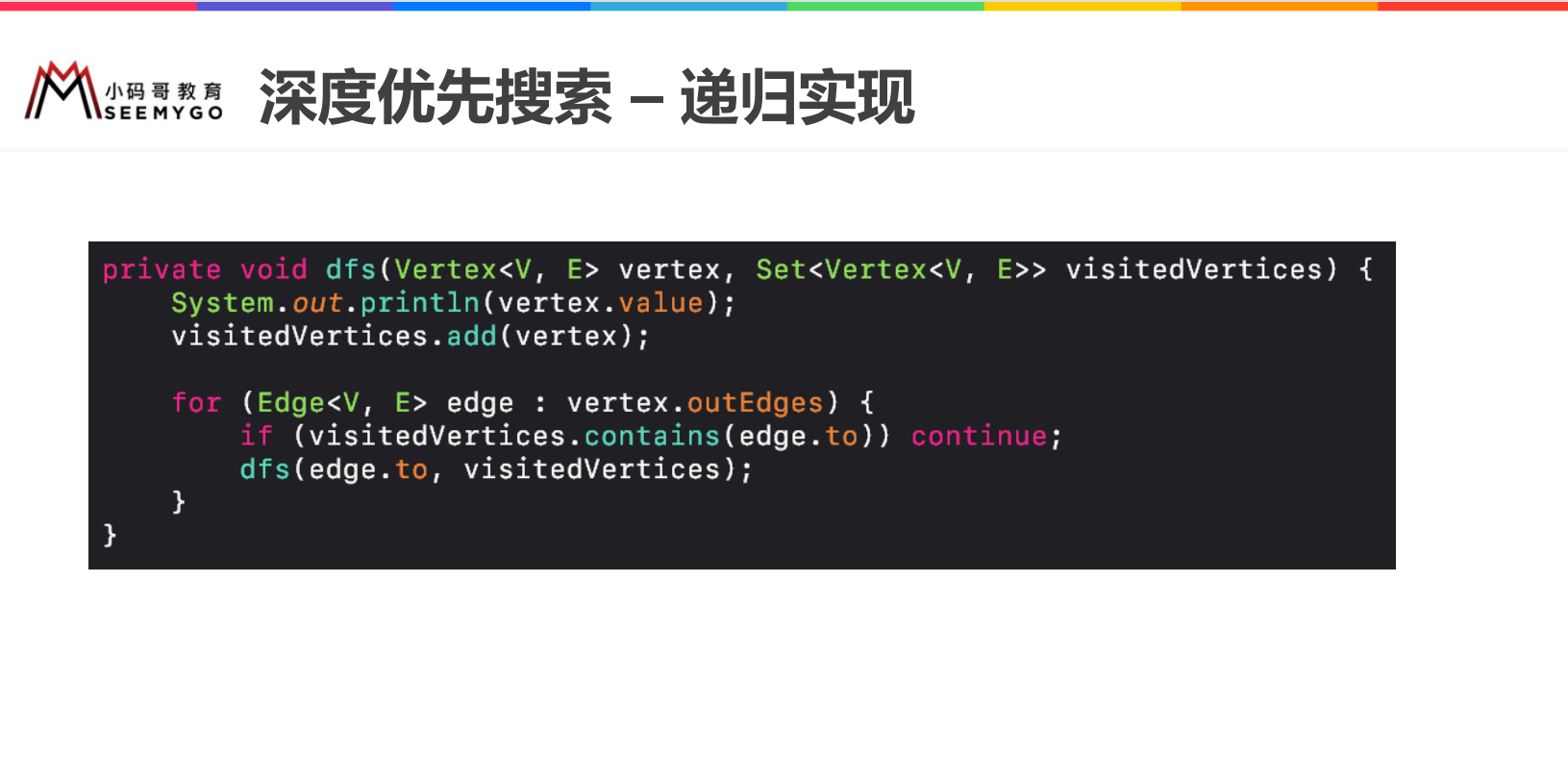
// Depth first search -- recursive implementation
@Override
public void dfs(V begin) {
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
dfs(beginVertex, new HashSet<>());
}
private void dfs(Vertex<V, E> vertex, Set<Vertex<V, E>> set) {
System.out.println(vertex);
set.add(vertex);
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
dfs(edge.to, set);
}
}
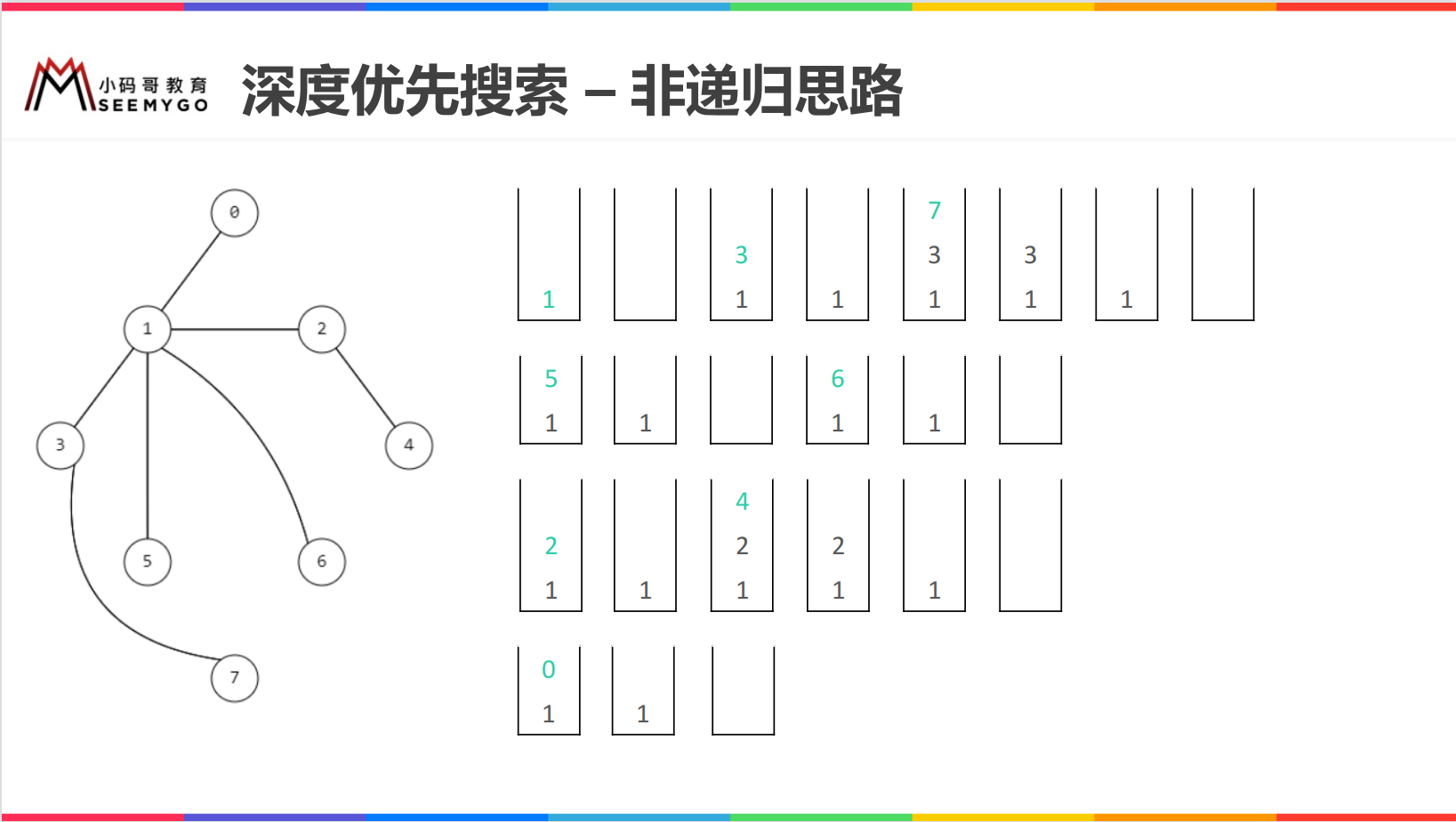

// Depth first search -- non recursive implementation
@Override
public void dfs(V begin) {
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Set<Vertex<V, E>> set = new HashSet<>();
Stack<Vertex<V, E>> stack = new Stack<>();
stack.push(beginVertex);
set.add(beginVertex);
System.out.println(beginVertex);
while (!stack.isEmpty()) {
final Vertex<V, E> vertex = stack.pop();
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
stack.push(edge.from);
stack.push(edge.to);
set.add(edge.to);
System.out.println(edge.to);
break;
}
}
}
Modify traversal interface
public interface Graph<V, E> {
int vertexSize(); // Number of vertices
int edgeSize(); // Number of edges
void addVertex(V v); // Add a vertex
void removeVertex(V v); // Delete a vertex
void addEdge(V from, V to); // Add an edge / / if a vertex does not exist, it will be created automatically
void addEdge(V from, V to, E weight); // Add an edge (with weight) / / if a vertex does not exist, it will be created automatically
void removeEdge(V from, V to); // Delete an edge
// void bfs(V begin); // Breadth first search traversal
// void dfs(V begin); // depth first search
void bfs(V begin, Visitor<V> visitor); // Breadth first search traversal
void dfs(V begin, Visitor<V> visitor); // depth first search
interface Visitor<V> {
void vertex(V v);
}
}
// Breadth first search
@Override
public void bfs(V begin, Visitor<V> visitor) {
if (null == visitor) return;
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Queue<Vertex<V, E>> queue = new LinkedList<>();
Set<Vertex<V, E>> set = new HashSet<>();
queue.offer(beginVertex);
set.add(beginVertex);
while (!queue.isEmpty()) {
final Vertex<V, E> vertex = queue.poll();
visitor.vertex(vertex.value);
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
queue.offer(edge.to);
set.add(edge.to);
}
}
}
// Depth first search -- non recursive implementation
@Override
public void dfs(V begin, Visitor<V> visitor) {
if (null == visitor) return;
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Set<Vertex<V, E>> set = new HashSet<>();
Stack<Vertex<V, E>> stack = new Stack<>();
stack.push(beginVertex);
set.add(beginVertex);
visitor.vertex(beginVertex.value);
while (!stack.isEmpty()) {
final Vertex<V, E> vertex = stack.pop();
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
stack.push(edge.from);
stack.push(edge.to);
set.add(edge.to);
visitor.vertex(edge.to.value);
break;
}
}
// Depth first search -- recursive implementation
public void dfs2(V begin, Visitor<V> visitor) {
if (null == visitor) return;
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
dfs2(beginVertex, new HashSet<>(), visitor);
}
private void dfs2(Vertex<V, E> vertex, Set<Vertex<V, E>> set, Visitor<V> visitor) {
visitor.vertex(vertex.value);
set.add(vertex);
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
dfs2(edge.to, set, visitor);
}
}
}
If you want to stop (exit) traversal during traversal:
void bfs(V begin, Visitor<V> visitor); // Breadth first search traversal
void dfs(V begin, Visitor<V> visitor); // depth first search
// You can stop traversal
interface Visitor<V> {
boolean vertex(V v); // If true is returned, the traversal is terminated
}
// You can stop traversal
// Breadth first search
@Override
public void bfs(V begin, Visitor<V> visitor) {
if (null == visitor) return;
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Queue<Vertex<V, E>> queue = new LinkedList<>();
Set<Vertex<V, E>> set = new HashSet<>();
queue.offer(beginVertex);
set.add(beginVertex);
while (!queue.isEmpty()) {
final Vertex<V, E> vertex = queue.poll();
if (visitor.vertex(vertex.value)) return;
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
queue.offer(edge.to);
set.add(edge.to);
}
}
}
// Depth first search -- non recursive implementation
@Override
public void dfs(V begin, Visitor<V> visitor) {
if (null == visitor) return;
final Vertex<V, E> beginVertex = vertices.get(begin);
if (null == beginVertex) return;
Set<Vertex<V, E>> set = new HashSet<>();
Stack<Vertex<V, E>> stack = new Stack<>();
stack.push(beginVertex);
set.add(beginVertex);
if (visitor.vertex(beginVertex.value)) return;
while (!stack.isEmpty()) {
final Vertex<V, E> vertex = stack.pop();
for (Edge<V, E> edge : vertex.outEdges) {
if (set.contains(edge.to)) continue;
stack.push(edge.from);
stack.push(edge.to);
set.add(edge.to);
if (visitor.vertex(edge.to.value)) return;
break;
}
}
}
AOV network
Homework: self study AOV network
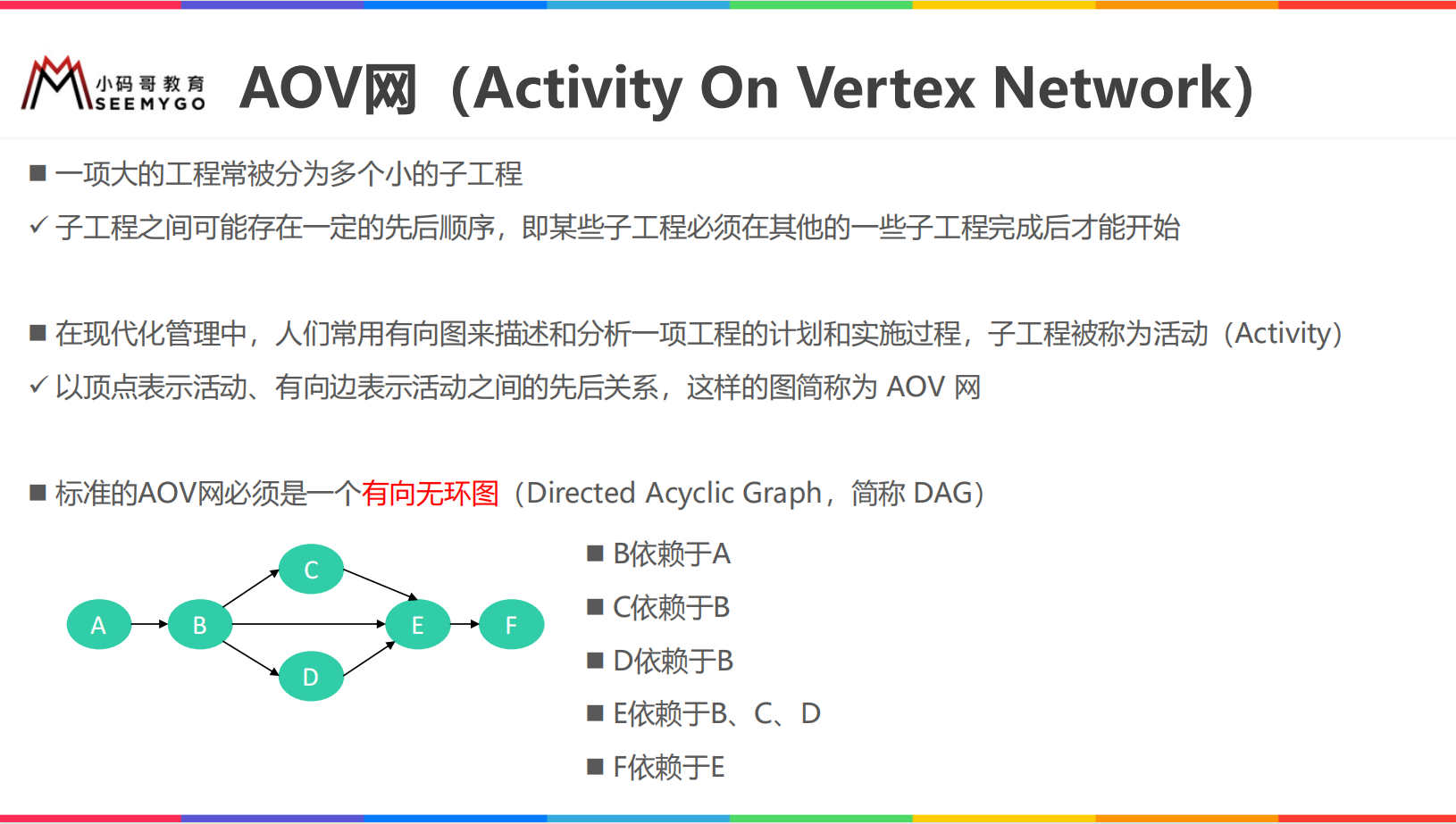
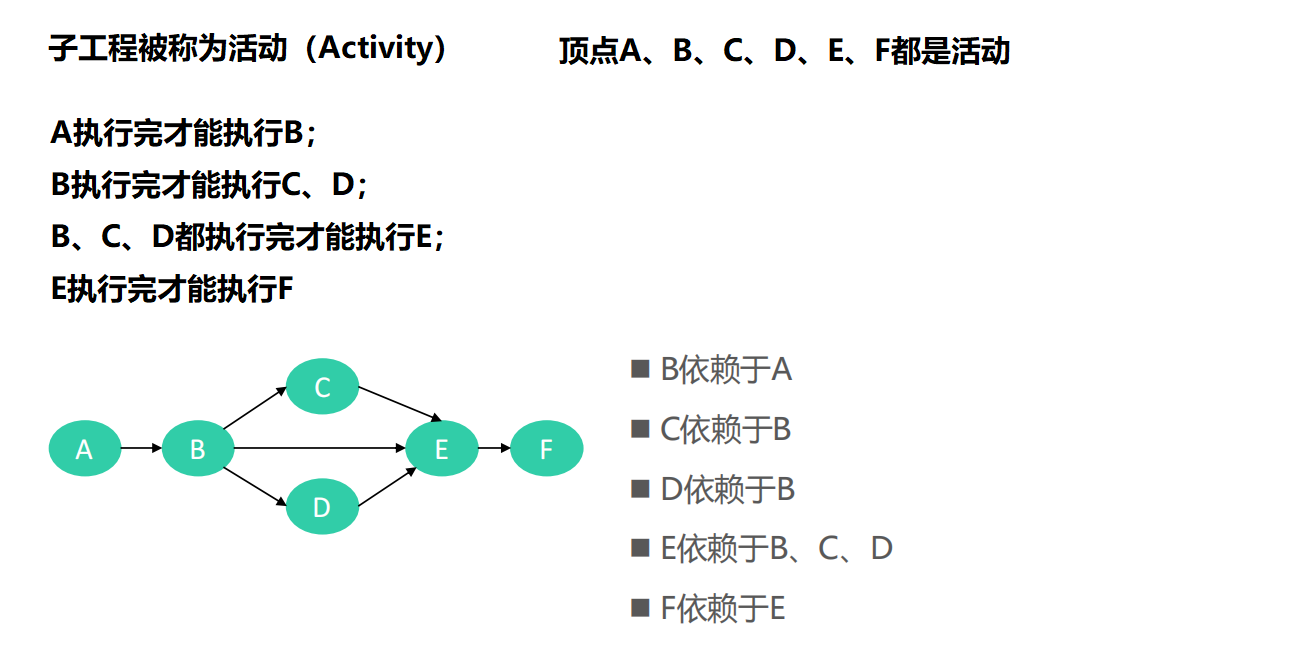
Topological sorting
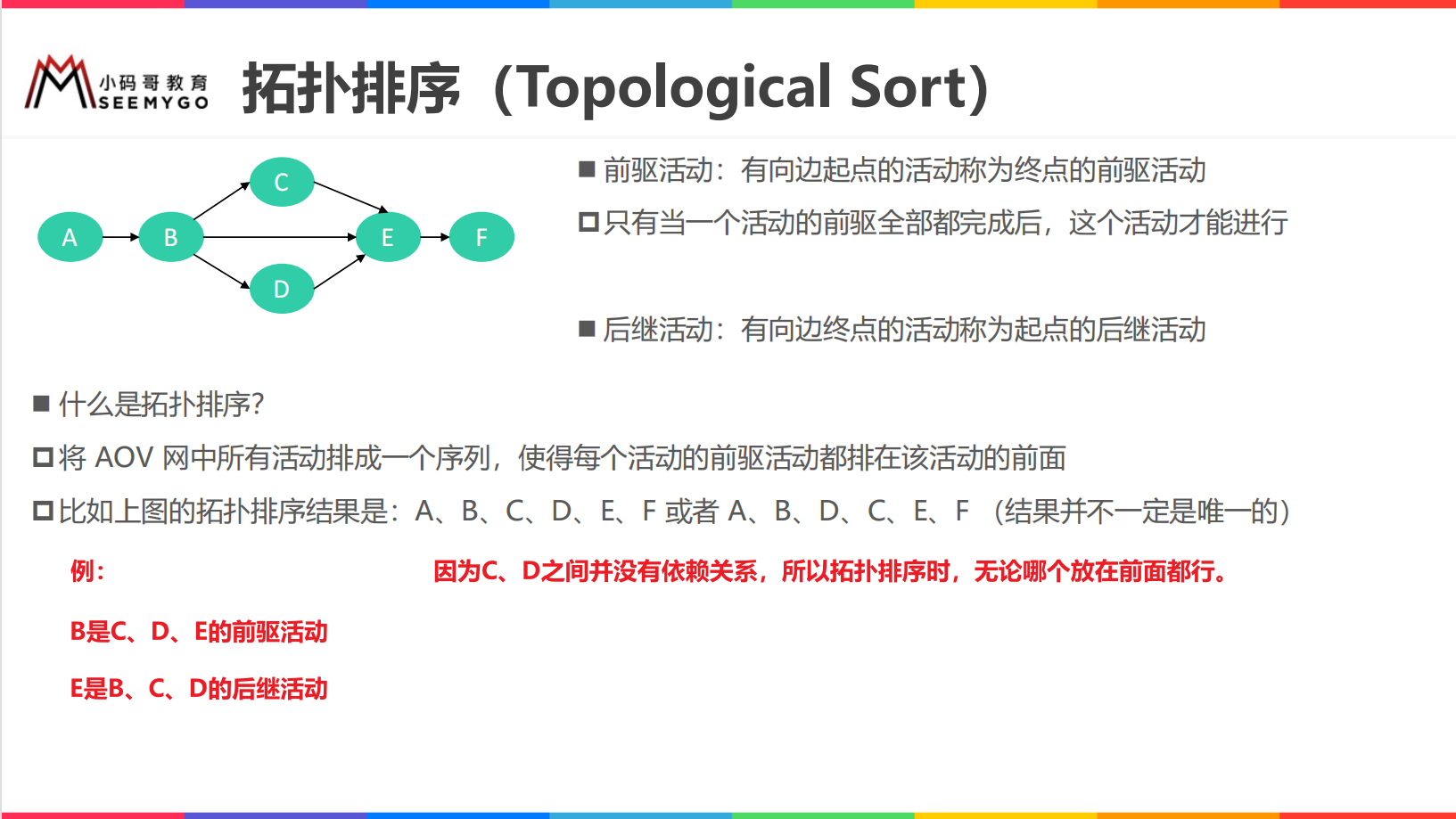
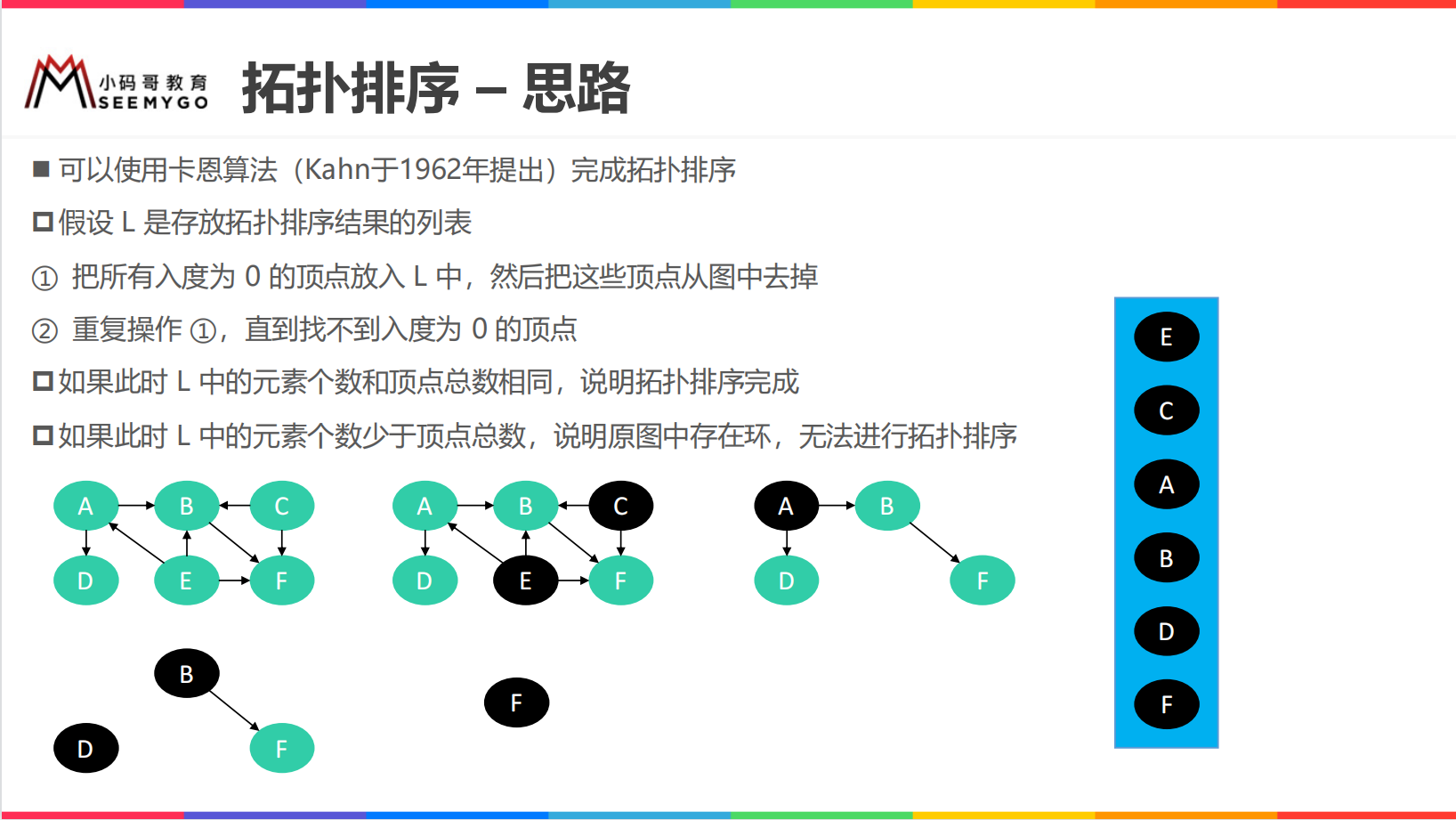
The idea of Kahn algorithm is right, but when implementing the code, we must not delete the vertices, because this will destroy the original graph structure. Therefore, when using Kahn algorithm to realize topological sorting, we should make some modifications:
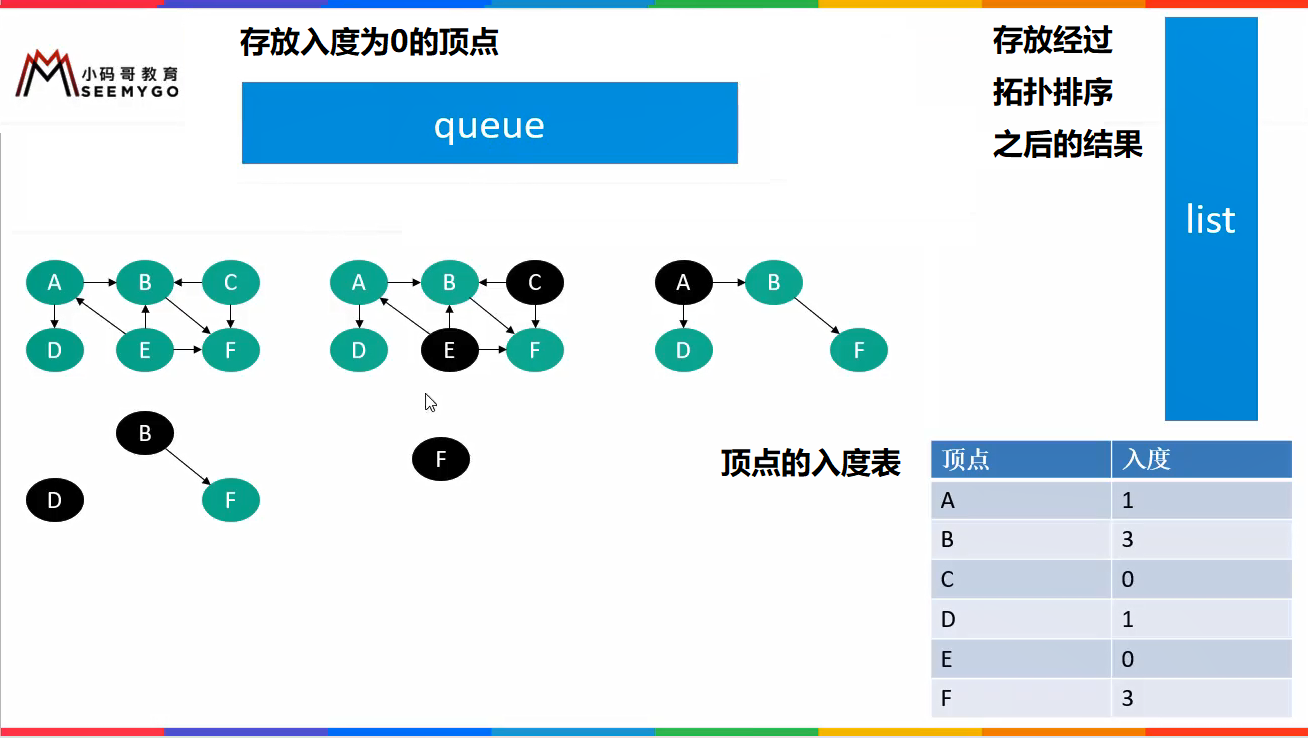
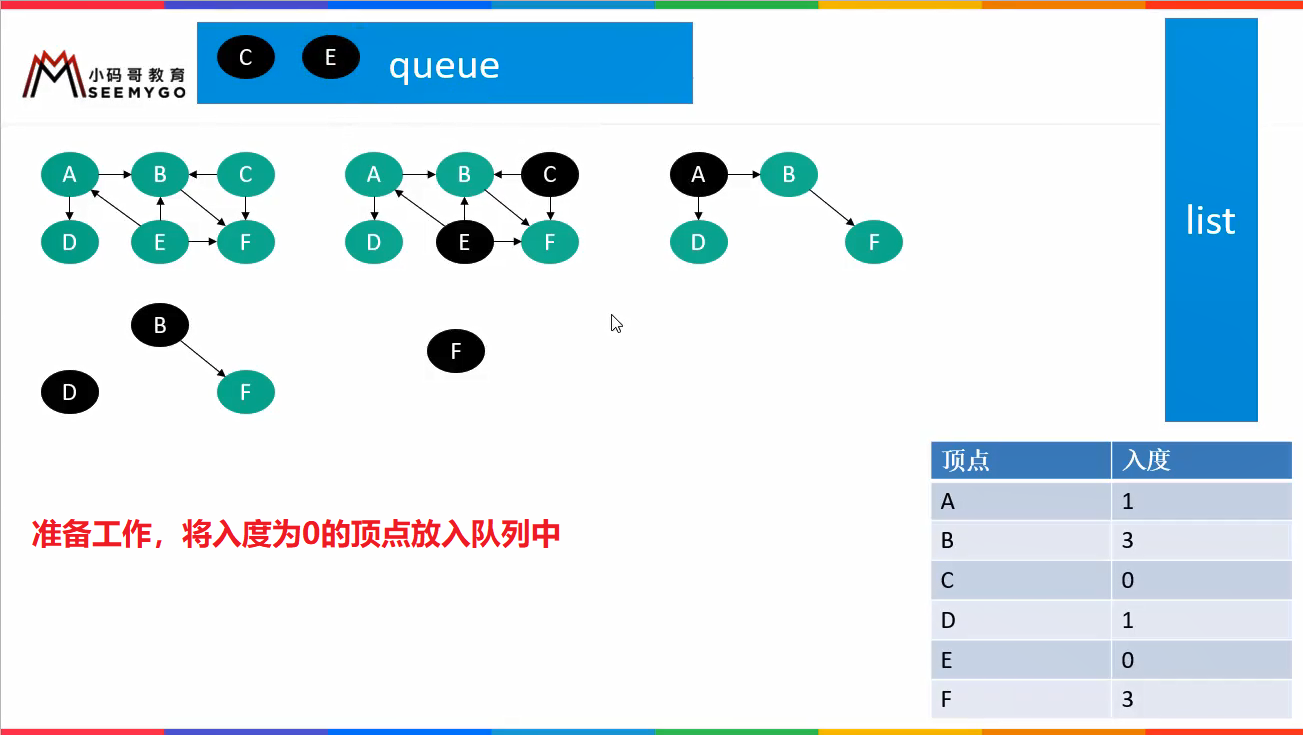
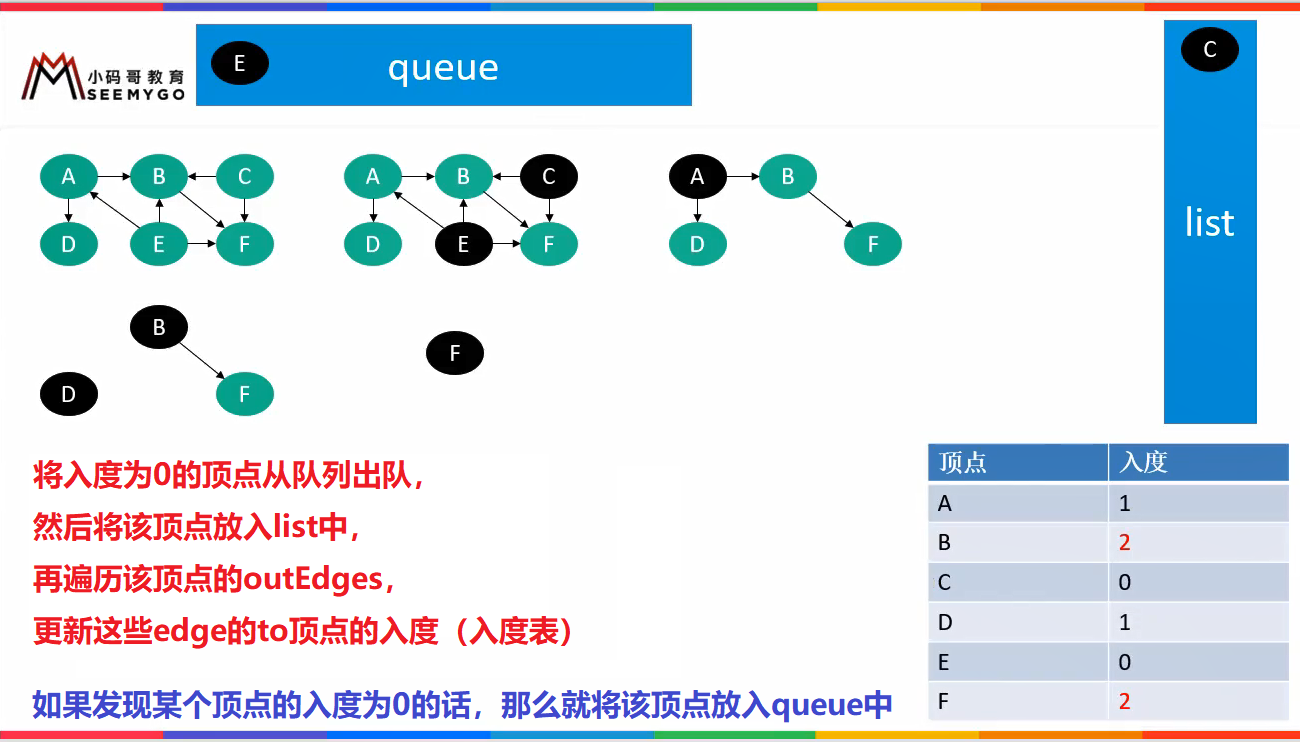

// The DAG is topologically sorted by Kahn algorithm
@Override
public List<V> topologicalSort() {
List<V> list = new ArrayList<>(); // list is used to store the traversal results and return them to the user
Queue<Vertex<V, E>> queue = new LinkedList<>(); // queue is used to store vertices with a penetration of 0
Map<Vertex<V, E>, Integer> map = new HashMap<>(); // Vertex entry table
// Initialize the degree table and queue (put the nodes with degree 0 into the queue)
vertices.forEach((v, vertex) -> {
int inSize = vertex.inEdges.size();
if (inSize == 0) queue.offer(vertex);
else
// When initializing the in meter, it is not necessary to put the vertices with the in degree of 0 into the in meter
map.put(vertex, inSize);
});
while (!queue.isEmpty()) {
Vertex<V, E> vertex = queue.poll();
list.add(vertex.value);
vertex.outEdges.forEach(edge -> {
Integer integer = map.get(edge.to);
integer--;
if (integer == 0)
// After joining this vertex into the team, you don't need to update the penetration of this vertex
queue.offer(edge.to);
else map.put(edge.to, integer);
});
}
return list;
}
Test:
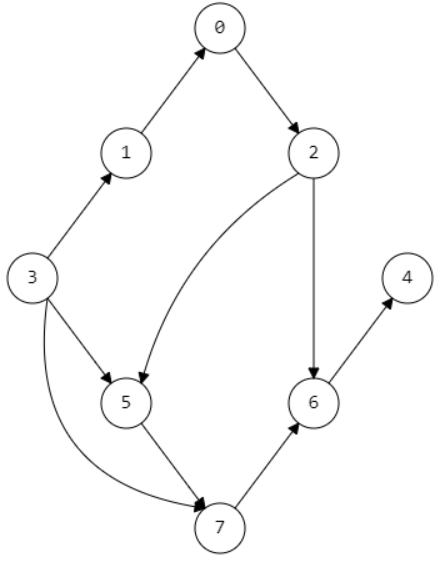
public class Data {
public static final Object[][] TOPO = {
{0, 2},
{1, 0},
{2, 5}, {2, 6},
{3, 1}, {3, 5}, {3, 7},
{5, 7},
{6, 4},
{7, 6}
};
}
/**
* Directed graph
*/
private static Graph<Object, Double> directedGraph(Object[][] data) {
Graph<Object, Double> graph = new ListGraph<>();
for (Object[] edge : data) {
if (edge.length == 1) {
graph.addVertex(edge[0]);
} else if (edge.length == 2) {
graph.addEdge(edge[0], edge[1]);
} else if (edge.length == 3) {
double weight = Double.parseDouble(edge[2].toString());
graph.addEdge(edge[0], edge[1], weight);
}
}
return graph;
}
/**
* Undirected graph
*/
private static Graph<Object, Double> undirectedGraph(Object[][] data) {
Graph<Object, Double> graph = new ListGraph<>();
for (Object[] edge : data) {
if (edge.length == 1) {
graph.addVertex(edge[0]);
} else if (edge.length == 2) {
graph.addEdge(edge[0], edge[1]);
graph.addEdge(edge[1], edge[0]);
} else if (edge.length == 3) {
double weight = Double.parseDouble(edge[2].toString());
graph.addEdge(edge[0], edge[1], weight);
graph.addEdge(edge[1], edge[0], weight);
}
}
return graph;
}
private static void testTopologicalSort() {
Graph<Object, Double> graph = directedGraph(Data.TOPO);
graph.topologicalSort().forEach(System.out::println);
}
public static void main(String[] args) {
testTopologicalSort();
}
reference resources
Little brother Li Mingjie's course: Fall in love with data structures and algorithms Season 2.
At the end of this article, thank you for your attention and support!