Recommend a blog post with a clear idea of quick sorting: https://blog.csdn.net/jiangtianjiao/article/details/88929408
The contents are as follows:
basic thought
Select a benchmark number and divide the data to be sorted into two independent parts through one-time sorting. All data in one part is smaller than all data in the other part. Then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so as to make all data orderly.

step
(1) Pick a reference value from the sequence.
(2) Place all smaller than the benchmark value in front of the benchmark, and all larger than the benchmark value behind the benchmark (the same number can be on either side). After the partition exits, the benchmark will be in the middle of the sequence.
(3) Recursively sort the subsequence before the reference value and the subsequence after the reference value.

Note: benchmark elements / left cursors / right cursors are for single pass sorting, that is to say, in the multi pass sorting of the whole sorting process, the benchmark elements / left cursors / right cursors obtained by each pass sorting are generally different. In principle, the selection of reference elements is arbitrary, but generally we select the first element in the array as the reference element (assuming that the array is randomly distributed).

The schematic diagram of sorting process is as follows:

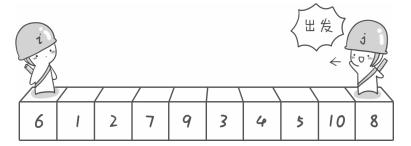
Select the first element 6 of the above array as the reference element. The left cursor is i sentinel and the right cursor is j sentinel. The rules they follow are as follows:
1, The right cursor scans to the left and crosses all array elements larger than the reference element until it encounters an array element less than or equal to the reference element and stops at that position. 2, The left cursor scans to the right, crossing all array elements that are smaller than the reference element, until it encounters an array element that is greater than or equal to the reference element, and stops at that position.

Step one: the sentry j starts out first. Because the reference number set here is the leftmost number, it is necessary to let sentry j start to move out first, and sentry j gradually moves to the left until an element less than 6 is found and stops. Next, the sentry i moves gradually to the right until it finds an element greater than 6 and stops. Finally, sentry i stopped in front of the number 7 and sentry j stopped in front of the number 5.

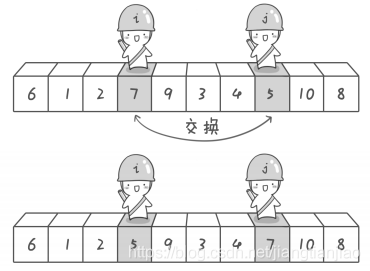
At the end of the first exchange, then sentry j continues to move to the left. It finds that 4 is smaller than the reference number 6, so it stops in front of the number 4. Sentry i then moves to the right, then stops in front of the number 9, and then sentry i and sentry j exchange again.

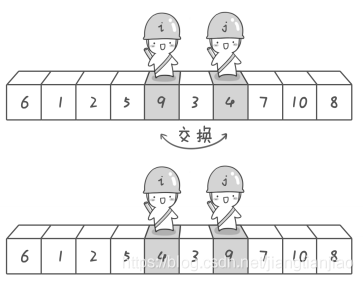
At the end of the second exchange, sentry j continued to move to the left and then stopped in front of the number 3; Sentry i continued to move to the right, but it found that it had met sentry j. At this time, the detection is completed, and the number 3 and the reference number 6 are exchanged.

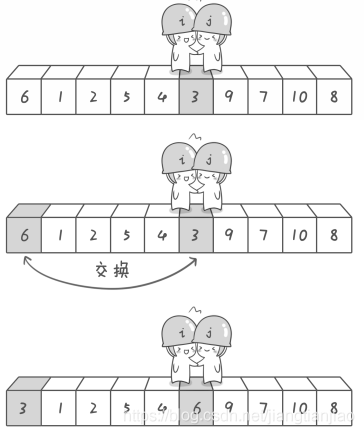
This is the real end of the first probe. At this time, with benchmark 6 as the dividing line, the array elements on the left are less than or equal to 6 and the array elements on the right are greater than or equal to 6. The left sequence is 3, 1, 2, 5, 4. The sequence on the right is 9, 7, 10 and 8. At this time, for the left sequence, take the number 3 as the reference element and repeat the above detection. The sequence after detection is 2, 1, 3, 5 and 4. For the sequence on the right, take the number 9 as the reference element, and repeat the above detection, divide step by step, and finally sort completely.

To sum up: quick sort is to continuously process an array with the idea of branching and recursion, and finally sort
The quick sort template is as follows:

def partition(nums,left, right): # Branch idea for benchmark index
    pivot = left
    i = left
    j = right
    while i<j:
        while i<j and nums[j]> nums[pivot]:
            j-=1
        while i<j and nums[i]< nums[pivot]:
            i+=1
        nums[i] , nums[j] = nums[j], nums[i]  #When you get to this step, it means that the value pointed by the right pointer is smaller than that of the sentry, and the value pointed by the left pointer is larger than that of the sentry. Exchange the two values pointed by the left and right pointers
    nums[pivot] , nums[i] = nums[pivot], nums[i] # When i and j meet, the traversal (detection) ends, and the value pointed by pivot is interchanged with the value pointed by i (J). At this time, Num [pivot] is the dividing line
    return i

def quick(nums, left, right): # The recursive idea is to sort the array
    if left>=right: # No sorting required
        return nums
    i = partition(nums, left, right)
    quick(nums, left, i-1)   #Call the function recursively and sort the left part of pivot
    quick(nums, i+1, right)  #Call the function recursively and sort the right part of pivot
    return nums

def quick_sort(nums): # Quick row
    n = len(nums)
    return quick(nums, 0, n-1)

You can also combine the partition() and quick() functions into one:

def quick_sort(nums):
    n = len(nums)
    return quick(nums, 0, n - 1)

def quick(nums,left, right):
    if left >= right:
        return nums
    pivot = left
    i = left
    j = right
    while i < j:
        while i < j and nums[j] > nums[pivot]:
            j -= 1
        while i < j and nums[i] <= nums[pivot]:
            i += 1
        nums[i], nums[j] = nums[j], nums[i]
    nums[pivot], nums[j] = nums[j], nums[pivot]
    quick(nums, left, j - 1)
    quick(nums, j + 1, right)
    return nums

The kth largest element in the Leetcode215 array

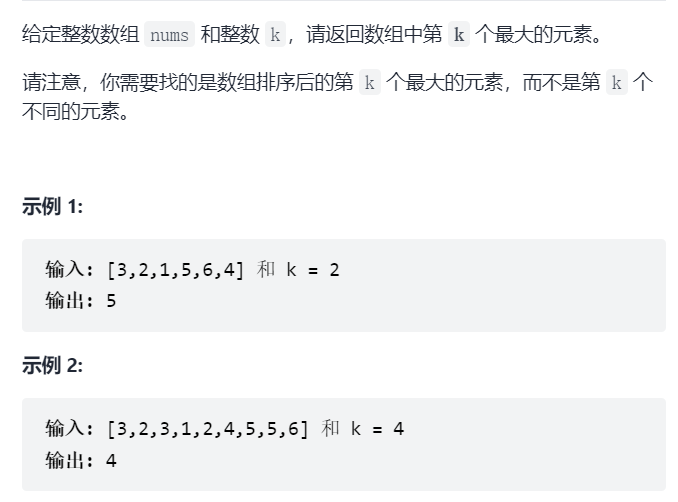
Idea: according to the divide and conquer idea of quic k sorting, we can determine the final position I of an element every time, and ensure that each element in num [left... i-1] is less than or equal to num [i], and num [i] is less than or equal to num [i + 1... right]. Therefore, as long as I of a partition is the penultimate subscript, we have found the answer

def topk_split(nums, k ,left, right):
	if left<right:
		index = partition(nums, left, right) 
		if index == k:
			return
		elif index< k: #
			topk_split(nums, k, left, index-1)
		else:
			topk_split(nums, k, index+1, right)

Get the number of the first k small

#Get the number of the first k small
def topk_smalls(nums, k):
    topk_split(nums, k, 0, len(nums)-1)
    return nums[:k]

arr = [1,3,2,3,0,-19]
k = 2
print(topk_smalls(arr, k))
print(arr)

Get the smallest number of k

#Get the smallest number k
def topk_small(nums, k):
    topk_split(nums, k, 0, len(nums)-1)
    return nums[k-1] #On the right is the open section, which requires - 1

arr = [1,3,2,3,0,-19]
k = 3
print(topk_small(arr, k))
print(arr)

Get the number of the first k

#Get the number of the first k 
def topk_larges(nums, k):
    #Parts are divided from small to large. If the left side of index is the first n-k small numbers, the right side of index is the first k large numbers
    topk_split(nums, len(nums)-k, 0, len(nums)-1) #Replace k with len(nums)-k
    return nums[len(nums)-k:] 

arr = [1,3,-2,3,0,-19]
k = 3
print(topk_larges(arr, k))
print(arr)

Get the k-th largest number

#Get the k-th largest number 
def topk_large(nums, k):
    #Parts are divided from small to large. If the left side of index is the first n-k small numbers, the right side of index is the first k large numbers
    topk_split(nums, len(nums)-k, 0, len(nums)-1) #Replace k with len(nums)-k
    return nums[len(nums)-k] 

arr = [1,3,-2,3,0,-19]
k = 2
print(topk_large(arr, k))
print(arr)

Sort only the first k small numbers

#Sort only the first k small numbers
#Obtain the number O(n) smaller than the first k and perform fast row O(klogk)
def topk_sort_left(nums, k):
    topk_split(nums, k, 0, len(nums)-1) 
    topk = nums[:k]
    quicksort(topk, 0, len(topk)-1)
    return topk+nums[k:] #Sort only the first k digits

arr = [0,0,1,3,4,5,0,7,6,7]
k = 4
topk_sort_left(arr, k)

Only the last k large numbers are sorted

#Only the last k large numbers are sorted
#Obtain the number O(n) that is smaller than the first n-k, and perform fast discharge O(klogk)
def topk_sort_right(nums, k):
    topk_split(nums, len(nums)-k, 0, len(nums)-1) 
    topk = nums[len(nums)-k:]
    quicksort(topk, 0, len(topk)-1)
    return nums[:len(nums)-k]+topk #Sort only the last k digits

arr = [0,0,1,3,4,5,0,-7,6,7]
k = 4
print(topk_sort_right(arr, k))