Placeholder

#A multiplication

Total score of this question: 5 points

Problem description

  Xiaolan found that he would 1 1 1 to 1000000007 1000000007 Different numbers between 1000000007 and 2021 2021 2021 multiply and then divide 1000000007 1000000007 The remainder of 100000007 will get different numbers.
  Xiaolan wants to know if she can 1 1 1 to 1000000007 1000000007 Find a number between 1000000007, and 2021 2021 2021 multiply and divide 1000000007 1000000007 The remainder after 100000007 is 999999999 999999999 999999999. If yes, please submit this number in the answer;
  if it does not exist, please submit it in the answer 0 0 0.

Answer submission

  this is a question to fill in the blank with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

17812964

Simple solution

  simple enumeration [ 1 , 1000000007 ] [1,1000000007] Every number in [11000000007] seems unwise, but in fact,

  for modern C P U \mathrm{CPU} For CPU, it is to sprinkle water.

  even yours C P U \mathrm{CPU} CPU dominant frequency is as low as 2.0 G h z 2.0\mathrm{Ghz} 2.0Ghz, which is also the calculation speed of 2 billion times per second.

  don't underestimate modern computers, asshole.

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 1000000007, M = 999999999;

    void run() {
        for (int i = 1; i <= N; i++)
            if (i * 2021L % N == M) System.out.println(i);
    }
}

Remainder definition

   remainder is defined as,

   give two integers a a a, b b b. Among them b ≠ 0 b \ne 0 b  = 0, then there must be two unique integers q q q, r r r. Make a = q b + r ， 0 ≤ r < ∣ b ∣ a=qb+r，0 \leq r < |b| a=qb+r，0≤r<∣b∣

    in this question, the last number we want to find, which may exist, can be expressed as,

   2021 ⋅ a ′ = 1000000007 ⋅ q + 999999999 2021 \cdot a' = 1000000007 \cdot q + 999999999 2021⋅a′=1000000007⋅q+999999999，

  obviously q q q will not exceed 2021 2021 2021，

   select the variable of enumeration as q q q, the enumeration range can be greatly reduced.

public class Test {

    public static void main(String[] args) { new Test().run(); }

    long N = 1000000007, M = 999999999;

    void run() {
        for (int i = 1; i < 2021; i++)
            if ((i * N + M) % 2021 == 0)
                System.out.println((i * N + M) / 2021);
    }
}

Congruence equation

extended euclidean algorithm

   according to the meaning of the topic, there is a congruence linear equation:

   a × x ≡ b ( m o d n ) a × x \equiv b \pmod{n} a×x≡b(modn)， gcd ⁡ ( a , n ) ∣ b \gcd(a,n) \mid b gcd(a,n)∣b

  will 2021 2021 2021 substitution a a a， 1000000007 1000000007 1000000007 substituted n n n， gcd ⁡ ( a , n ) = 1 \gcd(a,n)=1 gcd(a,n)=1, the equation has infinite solutions.

  a little explanation,

   a × x ≡ b ( m o d n ) a × x \equiv b \pmod{n} a × x ≡ b(modn) can be rewritten as a × x + n × y = b a × x + n × y = b a×x+n×y=b，

  find a group of numbers with extended Euclidean algorithm x 0 , y 0 x_{0}, y_{0} x0, y0, make a × x 0 + n × y 0 = gcd ⁡ ( a , n ) a × x_{0} + n × y_{0} = \gcd(a,n) a×x0​+n×y0​=gcd(a,n)，

  rule x = b × x 0 gcd ⁡ ( a , n ) x = \cfrac{b × x_{0}}{\gcd(a,n)} x=gcd(a,n)b × x0 is a solution of the original equation.

  the general solution is b × x 0 gcd ⁡ ( a , n )   m o d   n ‾ ( m o d n ) \overline{\cfrac{b × x_{0}}{\gcd(a,n)} \bmod n} \pmod{n} gcd(a,n)b×x0​​modn​(modn)，

                  n n n and x x Congruence classes of x congruences.

def exgcd(a, b):
    if b == 0:
        return (1, 0, a)
    (x, y, d) = exgcd(b, a % b)
    return (y, x - a // b * y, d);

(x, y, d) = exgcd(2021, 1000000007)
print((x * 999999999 // d) % (1000000007 // d))

  after all, it's the result of filling in the blank,

  just use it P y t h o n \mathrm{Python} Python wrote,

  put another one below J a v a \mathrm{Java} Java.

Fermat's theorem

  right a a a， a ∈ Z a \in \mathbb{Z} a ∈ Z, if p p p is prime, gcd ⁡ ( a , p ) = 1 \gcd (a,p) = 1 gcd(a,p)=1, yes

   a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod p ap−1≡1(modp)

  it's easy to sort out the equation,

   a x ≡ a p − 1 ( m o d p ) x ≡ a p − 2 ( m o d p ) b x ≡ b a p − 2 ≡ b ( m o d p ) \begin{aligned}ax & \equiv a^{p-1} &\pmod p\\x & \equiv a^{p-2} &\pmod p\\bx & \equiv ba^{p-2} \equiv b &\pmod p\end{aligned} axxbx​≡ap−1≡ap−2≡bap−2≡b​(modp)(modp)(modp)​

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int a = 2021, b = 999999999, p = 1000000007;

    void run() {
        System.out.println(pow(a, p - 2) * b % p);
    }

    long pow(int a, int n) {
        if (n == 1) return a;
        long res = pow(a, n >> 1);
        res = res * res % p;
        return (n & 1) == 1 ? res * a % p : res;
    }
}

   J a v a \mathrm{Java} Java is easier to implement.

#B straight line

Total score of this question: 5 points

Problem description

  in a plane rectangular coordinate system, two points can determine a straight line. If there are multiple points on a straight line, the straight line determined by any two of these points is the same.
  on a given plane 2 × 3 2 × 3 two × 3 full points { ( x , y ) ∣ 0 ≤ x < 2 , 0 ≤ y < 3 , x ∈ Z , y ∈ Z } \{(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z\} {(x,y) ∣ 0 ≤ x < 2,0 ≤ y < 3, X ∈ Z,y ∈ Z}, that is, the abscissa is 0 0 0 to 1 1 1 (inclusive) 0 0 0 and 1 1 1) The integer and ordinate between are 0 0 0 to 2 2 2 (inclusive) 0 0 0 and 2 2 2) Points between integers. These points have been determined 11 11 11 different lines.
  on a given plane 20 × 21 20 × 21 twenty × 21 hours { ( x , y ) ∣ 0 ≤ x < 20 , 0 ≤ y < 21 , x ∈ Z , y ∈ Z } \{(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z\} {(x,y) ∣ 0 ≤ x < 20,0 ≤ y < 21, X ∈ Z,y ∈ Z}, that is, the abscissa is 0 0 0 to 19 19 19 (inclusive) 0 0 0 and 19 19 19) The integer and ordinate between are 0 0 0 to 20 20 20 (inclusive) 0 0 0 and 20 20 20) Points between integers. How many different straight lines are determined by these points.

Answer submission

  this is a question to fill in the blank with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

40257

Set of linear equations

  a simple idea is to connect all points, remove duplicate lines, and then count.

   for the convenience of expression, the oblique section equation is adopted here y = k x + b y=kx+b y=kx+b to represent each straight line, where k k k is the slope of the straight line, b b b is a straight line at y y Intercept on the y-axis, and uniformly do not deal with the line where the slope does not exist, and add one to the result 20 20 20.

  attention! The result of this procedure is inaccurate.

import java.util.HashSet;
import java.util.Set;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int X = 20, Y = 21;

    void run() {
        Set<Line> set = new HashSet();
        for (int x1 = 0; x1 < X; x1++)
            for (int y1 = 0; y1 < Y; y1++)
                for (int x2 = x1; x2 < X; x2++)
                    for (double y2 = 0; y2 < Y; y2++)
                        if (x1 != x2){
                            double k = (y2 - y1) / (x2 - x1);
                            double b = -x1 * k + y1;
                            set.add(new Line(k, b));
                        }
        System.out.println(set.size() + X);
    }

    class Line {

        double k, b;

        Line(double b, double k) {
            this.k = k;
            this.b = b;
        }

        @Override
        public boolean equals(Object obj) {
            return k == ((Line)obj).k && b == ((Line)obj).b;
        }

        @Override
        public int hashCode() {
            return (int)k ^ (int)b;
        }
    }
}

Fraction elimination error

   when the slope is represented by floating-point numbers, the accuracy is uneven. It is true that the error can be limited to a range. When the absolute difference falls into it, we regard it as the same value.

   however, when the representable range is small, we can define the fraction to achieve no error, rather than control accuracy.

import java.util.HashSet;
import java.util.Set;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int X = 20, Y = 21;

    void run() {
        Set<Line> set = new HashSet();
        for (int x1 = 0; x1 < X; x1++)
            for (int y1 = 0; y1 < Y; y1++)
                for (int x2 = x1; x2 < X; x2++)
                    for (int y2 = 0; y2 < Y; y2++)
                        if (x1 != x2){
                            Fraction k = new Fraction(y2 - y1, x2 - x1);
                            Fraction b = new Fraction(y1 * (x2 - x1) - x1 * (y2 - y1),x2 - x1);
                            set.add(new Line(k, b));
                        }
        System.out.println(set.size() + X);
    }

    class Fraction {

        int numerator, denominator;

        Fraction(int numerator, int denominator) {
            int gcd = gcd(numerator, denominator);
            this.denominator = denominator /gcd;
            this.numerator = numerator / gcd;
        }

        int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

        @Override
        public boolean equals(Object obj) {
            return this.numerator == ((Fraction)obj).numerator && this.denominator == ((Fraction)obj).denominator;
        }
    }

    class Line {

        Fraction k, b;

        Line(Fraction b, Fraction k) {
            this.k = k;
            this.b = b;
        }

        @Override
        public boolean equals(Object obj) {
            return this.k.equals(((Line)obj).k) && this.b.equals(((Line)obj).b);
        }

        @Override
        public int hashCode() {
            return k.denominator;
        }
    }
}

Plane geometry

   this is a plane rectangular coordinate system, the origin and ( 1 , 2 ) (1,2) (1,2) connect into a line segment.

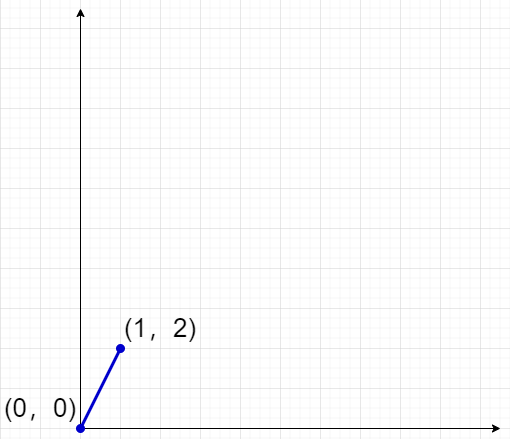
  we will mark the straight line passing through these two points and the point through which the straight line passes and the vertical line of the point on the horizontal and vertical axis.

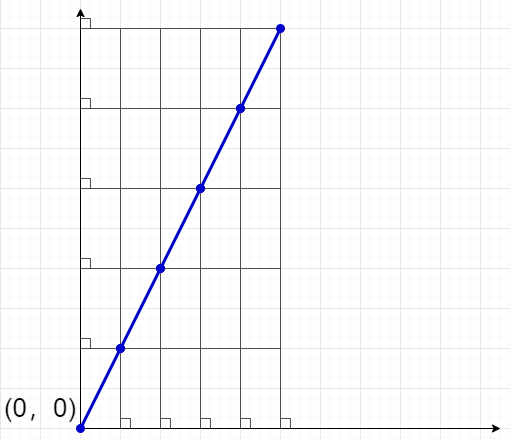
  obviously, if a straight line passes ( x 1 , y 1 ) (x_{1},y_{1}) (x1​,y1​), ( x 2 , y 2 ) (x_{2},y_{2}) (x2, y2) two points, then it must also pass through ( x 1 + k ( x 1 − x 2 ) , y 1 + k ( y 1 − y 2 ) ) (x_{1} +k(x_{1} - x_{2}),y_{1} + k(y_{1} - y_{2})) (x1​+k(x1​−x2​),y1​+k(y1​−y2​))， k ∈ Z k \in Z k∈Z.

   when connecting a straight line, mark the points through which all the straight lines pass, and we can skip directly the next time we encounter the marked two points.

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int X = 20, Y = 21;

    void run() {
        int count = 0;
        boolean[][][][] marked = new boolean[X][Y][X][Y];
        for (int x1 = 0; x1 < X; x1++)
            for (int y1 = 0; y1 < Y; y1++) {
                marked[x1][y1][x1][y1] = true;
                for (int x2 = 0; x2 < X; x2++)
                    for (int y2 = 0; y2 < Y; y2++) {
                        if (marked[x1][y1][x2][y2]) continue;
                        int x = x1, y = y1, xOffset = x - x2, yOffset = y - y2;
                        while (x >= 0 && x < X && y >= 0 && y < Y) {
                            x += xOffset;
                            y += yOffset;
                        }
                        x -= xOffset;
                        y -= yOffset;
                        while (x >= 0 && x < X && y >= 0 && y < Y) {
                            for (int i = x - xOffset, j = y - yOffset; i >= 0 && i < X && j >= 0 && j < Y; i -= xOffset, j -= yOffset) {
                                marked[x][y][i][j] = marked[i][j][x][y] = true;
                            }
                            x -= xOffset;
                            y -= yOffset;
                        }
                        count++;
                    }
            }
        System.out.println(count);
    }
}

   I think we may get another similar test. Here's a inference for everyone.

   on the plane rectangular coordinate system n × n n × n n×n， n ≥ 2 n \ge 2 n ≥ 2 points { ( x , y ) ∣ 0 ≤ x < n , 0 ≤ y < n , x ∈ Z , y ∈ Z } \{(x, y)|0 ≤ x < n, 0 ≤ y < n, x ∈ Z, y ∈ Z\} {(x,y) ∣ 0 ≤ x < n, 0 ≤ y < n, X ∈ Z,y ∈ Z}, the different lines that can be connected from the origin are 1 ≤ x , y < n 1 \leq x,y <n 1≤x,y<n， x ≠ y x \ne y x  = in y g c d ( x , y ) = 1 gcd(x,y) = 1 gcd(x,y)=1 times plus 3 3 3.

  interested readers can prove it by themselves.

  at the same time 1 ≤ x < y < n 1 \leq x < y < n When 1 ≤ x < y < n, g c d ( x , y ) = 1 gcd(x,y) = 1 The number of occurrences of gcd(x,y)=1 is exactly equal to ∑ y = 2 n − 1 φ ( y ) \displaystyle\sum_{y = 2}^{n-1}\varphi(y) y=2∑n−1​ φ (y) , where φ \varphi φ Is Euler function.

  capacity is limited, so we will not continue to discuss here.

#C. cargo placement

Total score of this question: 10 points

Problem description

  Xiaolan has a large warehouse, which can put a lot of goods.
  now, little blue has n n n boxes of goods shall be placed in the warehouse, and each box of goods is a regular cube. Xiaolan stipulates three mutually perpendicular directions of length, width and height. The side of each box of goods must be strictly parallel to the length, width and height.
  Xiaolan hopes that all the goods will eventually be placed into a big cube. That is, pile in the direction of length, width and height respectively L , W , H L,W,H 50. Goods of W and H meet n = L × W × H n = L × W × H n=L×W×H.
  given n n n. How many schemes for stacking goods meet the requirements.
  for example, when n = 4 n = 4 When n=4, there are the following 6 6 6 schemes: 1 × 1 × 4 1×1×4 1×1×4, 1 × 2 × 2 1×2×2 1×2×2, 1 × 4 × 1 1×4×1 1×4×1, 2 × 1 × 2 2×1×2 2×1×2, 2 × 2 × 1 2 × 2 × 1 2×2×1, 4 × 1 × 1 4 × 1 × 1 4×1×1.
  excuse me, when n = 2021041820210418 n = 2021041820210418 n=2021041820210418 (Note: 16 16 16 digits), how many schemes are there in total?
  tip: it is recommended to use computer programming to solve the problem.

Answer submission

  this is a question to fill in the blank with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

2430

Violent search

  basic arithmetic theorems that must be tested in each session.

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    long n = 2021041820210418L;

    void run() {
        List<Integer> exps0 = new ArrayList();
        ArrayDeque<Integer> exps1 = new ArrayDeque();
        for (int k = 2; k <= n; k++)
            if (n % k == 0) {
                int e = 0;
                while (n % k == 0) {
                    n /= k;
                    e++;
                }
                exps0.add(e);
            }
        System.out.println(dfs(exps0, exps1, 0));
    }

    int dfs(List<Integer> exps0, ArrayDeque<Integer> exps1, int cur) {
        if (cur == exps0.size()) {
            int comb = 1;
            for (int exp : exps1)
                comb *= exp + 1;
            return comb;
        }
        int ans = 0;
        for (int i = exps0.get(cur); i >= 0; i--) {
            exps1.push(i);
            ans += dfs(exps0, exps1, cur + 1);
            exps1.pop();
        }
        return ans;
    }
}

  it's not impossible to set two for directly, but the program written in this way usually can't run until the end of the game.

  therefore, we should avoid the judgment of invalid factors,

   the statistics here is that the qualitative factor is divided into three parts and the number of possible combinations, which is equivalent to the original proposition.

  there's nothing to say.

Scaling quality factor

  for example,

  when n = 9 n = 9 When n=9 ， yes 6 6 6 schemes: 1 × 1 × 9 1×1×9 1×1×9, 1 × 3 × 3 1×3×3 1×3×3, 1 × 9 × 1 1×9×1 1×9×1, 3 × 1 × 3 3×1×3 3×1×3, 3 × 3 × 1 3 × 3 × 1 3×3×1, 9 × 1 × 1 9 × 1 × 1 9×1×1;

  when n = 25 n = 25 When n=25, yes 6 6 6 schemes: 1 × 1 × 25 1×1×25 1×1×25, 1 × 5 × 5 1×5×5 1×5×5, ⋯ \cdots ⋯ ;

  when n = p 2 n =p^{2^{}} When n=p2, there is 6 6 6 schemes: 1 × 1 × p 2 1×1×p^{2} 1×1×p2, 1 × p × p 1×p×p 1×p×p, ⋯ \cdots ⋯ ;

  where p p p is a prime number.

   in fact, in the above example solution, we can find that the number of combinations has nothing to do with its specific value, it is only linked to the quality factor index.

   2021041820210418 = 2 × 3 3 × 17 × 131 × 2857 × 5882353 2021041820210418 = 2 × 3^3 × 17 × 131 × 2857 × 5882353 2021041820210418=2×33×17×131×2857×5882353

  if we find the smallest prime numbers to replace them, we get the new numbers 2 3 × 3 × 5 × 7 × 11 × 13 = 120120 2^3 × 3 × 5 × 7 × 11 × 13 = 120120 twenty-three × three × five × seven × eleven × 13 = 120120 and 2021041820210418 2021041820210418 2021041820210418 is equivalent under this proposition.

  and 120120 120120 The size of 120120 is enough. We found the combination of all its factors.

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    long N = 2021041820210418L;

    void run() {
        List<Integer> exps = new ArrayList();
        for (int k = 2; k <= N; k++)
            if (N % k == 0) {
                int e = 0;
                while (N % k == 0) {
                    N /= k;
                    e++;
                }
                exps.add(e);
            }
        exps.sort((a, b) -> (b - a));
        int n = 1, p = 2, ans = 0;
        for (int exp : exps) {
            for (int i = 2; i * i <= p; i++)
                if (p % i == 0) {
                    i = 1;
                    p++;
                }
            while (exp-- > 0) n *= p;
            p++;
        }
        for (int a = 1; a <= n; a++)
            if (n % a == 0)
                for (int b = 1; b <= n; b++)
                    if (n / a % b == 0) ans++;
        System.out.println(ans);
    }
}

#D path

Total score of this question: 10 points

Problem description

  Xiaolan is very happy after learning the shortest path. He defines a special graph and hopes to find the shortest path in the graph.
  the picture of little blue 2021 2021 2021 nodes, numbered in sequence 1 1 1 to 2021 2021 2021. For two different nodes a , b a, b a. B. If a a a and b b The absolute value of the difference of b is greater than 21 21 21, then there is no edge connection between the two nodes; If a a a and b b The absolute value of the difference of b is less than or equal to 21 21 21, then there is a line between the two points with a length of a a a and b b The undirected edge of the least common multiple of b is connected.
  for example: node 1 1 1 and node 23 23 There is no edge connection between 23; node 3 3 3 and nodes 24 24 There is an undirected edge between 24, with a length of 24 24 24； node 15 15 15 and nodes 25 25 There is an undirected edge between 25 with a length of 75 75 75.
  please calculate, node 1 1 1 and node 2021 2021 What is the shortest path length between 2021.
  tip: it is recommended to use computer programming to solve the problem.

Answer submission

  this is a question to fill in the blank with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

10266837

  the topic has been made clear enough,

  build a 2021 2021 2021 vertices 21 × 2000 + 21 ( 21 + 1 ) 2 21 × 2000 + \cfrac{21(21 + 1)}{2} twenty-one × For an undirected graph with 2000 + 221 (21 + 1) edges, the algorithm on the running graph is finished.

  another detail is whether the plastic surgery will overflow. We take ( 1 , 2021 ] (1,2021] The largest prime number in [12021] 2017 2017 2017 and 202 1 2 2021^2 The result obtained by multiplying 20212 is a little exaggerated. Although it has been tested, the possible line weight combination will not exceed at most 2 31 − 1 2^{31} - 1 231 − 1, but after all, it is competition oriented. Considering the time cost of screening, it is more cost-effective to directly use long plastic surgery.

search

Depth first search

   2021 2021 2021 vertices, most of which are connected 2 × 21 2 × 21 two × 21 sides,

  don't search deeply, just search

  compilaition completed successfully in 500ms(4 hour ago)

  just, the computer is facing the player and goes to jail.

Memory search

   depth first search. When searching for the best result, you usually need to completely enumerate all possible problem states.

   but in the set of problem States, the "suffix" of all options is the same, that is, all optional branches end with the same node.

  if we save the shortest path from the searched node to the target node, we will return directly when we search the branch of this "suffix" again.

  then the problem may be solved in a relatively short time.

  this is also the so-called memory search.

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    int[] weight = new int[N + 1];

    List<Edge>[] graph = new List[N + 1];

    boolean[] visited = new boolean[N + 1];

    void run() {
        for (int i = 1; i <= N; i++)
            graph[i] = new ArrayList();
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        visited[1] = true;
        System.out.println(dfs(1));
    }

    int dfs(int v) {
        if (v == N) return 0;
        if (weight[v] != 0) return weight[v];
        int min = 0x7FFFFFFF;
        for (Edge edge : graph[v]) {
            if (visited[edge.w]) continue;
            visited[edge.w] = true;
            min = min(min, dfs(edge.w) + edge.weight);
            visited[edge.w] = false;
        }
        return weight[v] = min;
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }
}

Pruning and searching

  in fact, simple search, whether deep search or wide search, is a very aggressive behavior in the competition,

  there are too many factors affecting the execution efficiency of these two algorithms.

   of course, if there are no other ideas, we can only treat a dead horse as a living horse doctor.

  fortunately, the results can be calculated in a very short time with simple branch scissors

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Queue;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;
    
    void run() {
        List<Edge>[] graph = new List[N + 1];
        long[] visited = new long[N + 1];
        for (int i = 1; i <= N; i++)
            graph[i] = new ArrayList();
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        Queue<Vertex> queue = new PriorityQueue();
        Arrays.fill(visited, Long.MAX_VALUE);
        queue.offer(new Vertex(1, 0));
        Vertex V = null;
        while (queue.size() > 0) {
            V = queue.poll();
            if (V.v == N) break;
            if (V.weight >= visited[V.v]) continue;
            visited[V.v] = V.weight;
            for (Edge edge : graph[V.v])
                queue.offer(new Vertex(edge.w, edge.weight + V.weight));
        }
        System.out.println(V.weight);
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }

    class Vertex implements Comparable<Vertex> {

        int v;
        long weight;

        Vertex(int v, long weight) {
            this.weight = weight;
            this.v = v;
        }

        @Override
        public int compareTo(Vertex V) { return Long.compare(this.weight, V.weight); }
    }
}

Single source shortest path

Dijkstra

   the graph given in the title is obviously an undirected graph with edge weighting and non negative weight. Run all over D i j k s t r a Dijkstra Dijkstra is done.

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Queue;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        boolean[] marked = new boolean[N + 1];
        List<Edge>[] graph = new List[N + 1];
        long[] distTo = new long[N + 1];
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList();
            distTo[i] = Long.MAX_VALUE;
        }
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        Queue<Vertex> queue = new PriorityQueue();
        queue.offer(new Vertex(1, distTo[1] = 0));
        while (queue.size() > 0) {
            Vertex V = queue.poll();
            if (marked[V.v])
                    continue;
            marked[V.v] = true;
            for (Edge edge : graph[V.v])
                if (distTo[edge.w] > distTo[V.v] + edge.weight)
                    queue.offer(new Vertex(edge.w, distTo[edge.w] = distTo[V.v] + edge.weight));
        }
        System.out.println(distTo[N]);
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }

    class Vertex implements Comparable<Vertex> {

        int v;
        long dist;

        Vertex(int v, long dist) {
            this.dist = dist;
            this.v = v;
        }

        @Override
        public int compareTo(Vertex V) { return Long.compare(this.dist, V.dist); }
    }
}

Floyd

  if it is the result of the shortest path.

  it can run within the competition time limit O ( n 3 ) O(n^{3}) O(n3).

  that's actually no brain trap F l o y d Floyd Just Floyd.

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        long[][] floyd = new long[N + 1][N + 1];
        for (int v = 1; v < N; v++)
            for (int w = v + 1; w <= min(N, v + 21); w++)
                floyd[v][w] = floyd[w][v] = lcm(v, w);
        for (int k = 1; k <= N; k++)
            for (int v = 1; v <= N; v++)
                if (floyd[v][k] == 0) continue;
                else for (int w = 1; w <= N; w++)
                    if (floyd[k][w] == 0) continue;
                    else if (floyd[v][w] == 0 || floyd[v][k] + floyd[k][w] < floyd[v][w])
                        floyd[v][w] = floyd[v][k] + floyd[k][w];
        System.out.println(floyd[1][N]);
    }

    long min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
}

  I'll be out in half a minute, OK.

#E loop count

Total score of this question: 15 points

Problem description

  blue bridge College 21 21 It is composed of 21 teaching buildings with teaching building number 1 1 1 to 21 21 21. For two teaching buildings a a a and b b b. When a a a and b b b in case of Coprime, a a a and b b b there is a corridor directly connected between them, which can pass in both directions, otherwise there is no corridor directly connected.
  Xiao Lan is now in the first teaching building. He wants to visit each teaching building exactly once and finally return to the first teaching building (i.e. take a Hamilton loop). How many different access schemes does he have? The difference between the two access schemes means that there is a i i i. Xiao Lan visited the teaching building in two ways i i After i visited different teaching buildings.
  tip: it is recommended to use computer programming to solve the problem.

Answer submission

  this is a question to fill in the blank with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

881012367360

Memory search

  the title description can obviously form an edge set with a size of ∑ i = 1 21 φ ( i ) = 140 \displaystyle\sum_{i=1}^{21} \varphi (i) = 140 i=1∑21​ φ (i)=140, the complexity of ergodic graph is estimated as O ( ∏ i = 1 n φ ( i ) ) O(\prod_{i=1}^n \varphi(i)) O(∏i=1n​φ(i))，

  violent search seems not feasible, but we can use certain optimization methods and memory processing to make it calculate the results in an acceptable time.

  design f v , s t a t u s f_{v,status} fv,status = from v v Start at v and go through s t a t u s status Number of schemes in status, s t a t u s status status in binary representation, the second i i i bit is 1 1 1 means to pass i i i point.

  then the answer is ∑ v = 2 21 f v , s t a t u s − v − 1 \displaystyle\sum_{v = 2}^{21} f_{v,status - v-1} v=2 Σ 21 fv,status − v − 1, because 1 1 1 and how to be greater than 1 1 The integer coprime of 1, that is, it can be obtained from any point 1 1 For point 1, we only need to count the number of paths through the whole graph divided by point 1.

  then [ 2 , n ] [2,n] [2,n] map to [ 0 , n − 2 ] [0, n - 2] [0,n − 2] optimize certain performance,

╭ last 3 3 It's quite unexpected that it can run in 3s.

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 21;

    long[][] cnt = new long[N - 1][1 << N - 1];

    List<Integer>[] graph = new List[N];

    void run() {
        for (int i = 0; i < N; i++)
            graph[i] = new ArrayList();
        for (int i = 2; i <= N; i++)
            for (int j = 2; j < i; j++)
                if (gcd(i, j) == 1){
                    graph[i - 2].add(j - 2);
                    graph[j - 2].add(i - 2);
                }
        for (int i = 0; i < cnt.length; i++)
            for (int j = 0; j < cnt[i].length; j++) cnt[i][j] = -1;
        long sum = 0;
        for (int i = 0; i < N - 1; i++)
            sum += dfs(i, (1 << N - 1) - 1 - (1 << i));
        System.out.println(sum);
    }

    long dfs(int start, int status) {
        if (status == 0) return 1;
        if (cnt[start][status] != -1) return cnt[start][status];
        long sum = 0;
        for (int v : graph[start])
            if ((status & (1 << v)) > 0)
                sum += dfs(v, status - (1 << v));
        return cnt[start][status] = sum;
    }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
}

  memory search is like pressure d p \mathrm{dp} Recursive implementation of dp,

  written to A \mathrm{A} There is no need to implement the words of group A,

That is to say.

#F minimum weight

time limit: 1.0 1.0 1.0s memory limit: 512.0 512.0 512.0MB total score of this question: 15 15 15 points

Problem description

  you have a balance. Now you have to design a set of weights, so that you can use these weights to weigh any less than or equal to N N The positive integer weight of N.
  how many weights should this set of weights contain at least?
  note that the weight can be placed on both sides of the balance.

Input format

  the input contains a positive integer N N N.

Output format

   output an integer representing the answer.

Test example 1

Input: 
7

Output: 
3

Explanation: 
3 The weights are 1, 4 and 6, which can weigh all the weights from 1 to 7.
1 = 1；
2 = 6 − 4 (Put 6 on one side and 4 on the other)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
It is impossible to weigh all weights from 1 to 7 with less than 3 weights.

Scale and agreement of evaluation cases

  for all evaluation cases, 1 ≤ N ≤ 1000000000 1 ≤ N ≤ 1000000000 1≤N≤1000000000.

Variant ternary

  a set contains n n n numbers, any number can be added or subtracted, and any number less than or equal to N N A positive integer of N.

  first of all, we should consider how to meet the nature of the subject requirements,

            i i The weight of i weights is w i w_{i} wi, original set A N = { w 1 , w 2 , ⋯   , w n } A_{N} = \{w_{1},w_{2},\cdots,w_{n}\} AN​={w1​,w2​,⋯,wn​}.

  to meet the meaning of the topic, we must first have s u m ( A ) ≥ N sum(A) \ge N sum(A)≥N，

  let's know A ⌊ N / 3 ⌋ A_{\lfloor N/3 \rfloor} A ⌊ N/3 ⌋ scheme, then we can add one to this scheme 2 ⌊ N / 3 ⌋ + 1 2\lfloor N/3 \rfloor + 1 2 ⌊ N/3 ⌋ + 1, you can use it 2 ⌊ N / 3 ⌋ + 1 2\lfloor N/3 \rfloor + 1 2 ⌊ N/3 ⌋ + 1 pair A ⌊ N / 3 ⌋ A_{\lfloor N/3 \rfloor} Several elements in A ⌊ N/3 ⌋ are expressed by difference ( ⌊ N / 3 ⌋ , 2 ⌊ N / 3 ⌋ + 1 ) (\lfloor N/3 \rfloor, 2\lfloor N/3 \rfloor + 1) (⌊ N/3 ⌋, 2 ⌊ N/3 ⌋ + 1), which is expressed by summing several elements ( 2 ⌊ N / 3 ⌋ + 1 , N ] (2\lfloor N/3 \rfloor + 1, N] (2 ⌊ N/3 ⌋ + 1,N], incorporated A ⌊ N / 3 ⌋ A_{\lfloor N/3 \rfloor} A ⌊ N/3 ⌋ itself can represent the range, that is, it can represent any less than or equal to N N A positive integer of N.

  if A ⌊ N / 3 ⌋ A_{\lfloor N/3 \rfloor} A ⌊ N/3 ⌋ itself is optimal, so add it K = 2 ⌊ N / 3 ⌋ + 1 K = 2\lfloor N/3 \rfloor + 1 K=2 ⌊ N/3 ⌋ + 1 A N A_N AN ， must also be optimal, because to make K + s u m ( A ⌊ N / 3 ⌋ ) ≥ N K + sum(A_{\lfloor N/3 \rfloor}) \ge N K+sum(A⌊N/3⌋​)≥N， K K Must be greater than or equal to K 2 ⌊ N / 3 ⌋ + 1 2\lfloor N/3 \rfloor + 1 2 ⌊ N/3 ⌋ + 1, and when K > 2 ⌊ N / 3 ⌋ + 1 K > 2\lfloor N/3 \rfloor + 1 K> When 2 ⌊ N/3 ⌋ + 1, it cannot be expressed ⌊ N / 3 ⌋ + 1 \lfloor N/3 \rfloor + 1 ⌊N/3⌋+1，

  of course, there is a prerequisite for all this, that is s u m ( A ⌊ N / 3 ⌋ ) = ⌊ N / 3 ⌋ sum(A_{\lfloor N/3 \rfloor}) = \lfloor N/3 \rfloor sum(A⌊N/3⌋​)=⌊N/3⌋. '

  but it's enough to inspire us to push forward,

  because the boundary of this problem is obvious,

  when N = 1 N = 1 When N=1, A 1 = { 1 } A_{1} = \{1\} A1​={1}，

  let's go A 1 A_{1} Added in A1 + 2 × s u m ( A 1 ) + 1 2 × sum(A_{1}) + 1 two × sum(A1) + 1, get A 4 A_{4} A4, i.e

  when N = 4 N = 4 When N=4, A 4 = { 1 , 3 } A_{4} = \{1,3\} A4​={1,3}，

  when N = 13 N = 13 When N=13, A 13 = { 1 , 3 , 9 } A_{13} = \{1,3,9\} A13​={1,3,9}，

   ⋯ ⋯ \cdots \cdots ⋯⋯

  of course, it still exists N N N is not in the optimal law we found.

  we set N = 5 N = 5 N=5，

  because A 4 = { 1 , 3 } A_{4} = \{1,3\} A4 = {1,3} optimality, 2 2 Two elements can form at most any less than or equal to 4 4 A positive integer of 4,

  because A 13 = { 1 , 3 , 9 } A_{13} = \{1,3,9\} A13 = {1,3,9} optimality, 3 3 Three elements can represent any less than or equal to 13 13 A positive integer of 13.

  that's right N = 5 N = 5 The answer given by N=5 must be greater than 2 2 2 less than or equal to 3 3 3.

  for any given N N N we can all find the answer according to this property.

  at the same time, look at this Law in ternary system:

   { N } = { ( 1 ) 3 , ( 11 ) 3 , ( 11 ) 3 , ⋯   } \{N\} = \{(1)_{3},(11)_{3},(11)_{3},\cdots\} {N}={(1)3​,(11)3​,(11)3​,⋯}

  it can be divided into two points, but it's not necessary.

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        long N = new Scanner(System.in).nextLong(), ans = 1;
        for (long pow3 = 1; pow3 < N; pow3 = pow3 * 3 + 1, ans++);
        System.out.println(ans);
    }
}

                   .

#G left child right brother

time limit: 3.0 3.0 3.0s memory limit: 512.0 512.0 512.0MB total score of this question: 20 20 20 points

Problem description

  for a multi fork tree, we can convert it into a binary tree through the representation of "left child and right brother".
  if we think that the child nodes of each node are disordered, the resulting binary tree may not be unique. In other words, each node can choose any child node as the left child and connect the right brothers in any order.
  a given tree contains N N N-node multitree, node from 1 1 1 to N N N number, where 1 1 Node 1 is the root, and the number of the parent node of each node is smaller than its own number. Please calculate the maximum height of the binary tree transformed by the representation of "left child and right brother". Note: the tree height of only the root node is 0 0 0 .
  for example, the following multi tree:

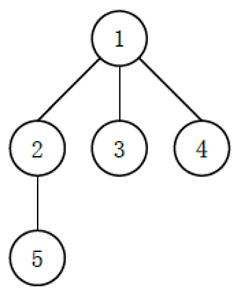
  there may be the following 3 3 3 (only listed here) 3 3 Three (but not all) different "left child right brother" means:

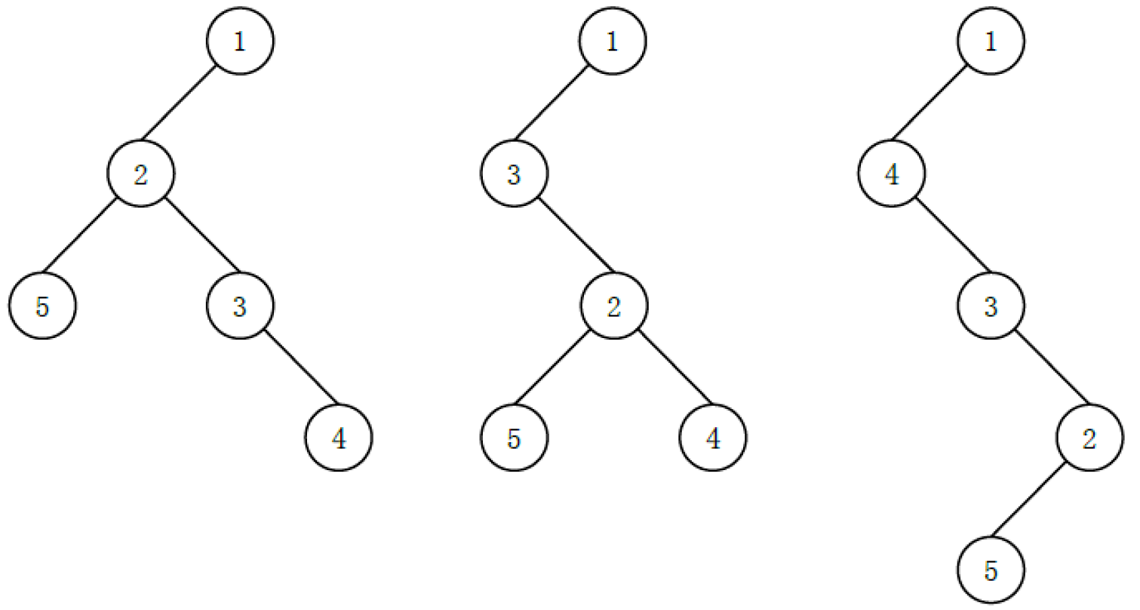
  the height of the last one is the highest, which is 4 4 4.

Input format

  the first line of input contains an integer N N N.
   below N − 1 N −1 N − 1 line, each line contains an integer, which is represented in turn 2 2 2 to N N The parent node number of node N.

Output format

   output an integer to represent the answer.

Test example 1

Input: 
5
1
1
1
2

Output: 
4

Scale and agreement of evaluation cases

  for 30 30 30% of the evaluation cases, 1 ≤ N ≤ 20 1 ≤ N ≤ 20 1≤N≤20；
  for all evaluation cases, 1 ≤ N ≤ 100000 1 ≤ N ≤ 100000 1≤N≤100000.

Tree DP

  the height of a tree is equal to the height of the highest subtree of the root node plus one,

  and a binary tree obtained from the representation of left child and right brother,

  we can put the largest subtree on the far right,

  under this strategy, the height of each subtree is the number of subtrees plus the height of the highest subtree.

  obviously right

  then there is the state transition equation: d p ( v ) = c o u n t ( s o n ( v ) ) + m a x { d p ( s o n ( v ) ) } dp(v) = \mathrm{count(son(}v\mathrm{))} + \mathrm{max\{}dp\mathrm{(son(}v\mathrm{))\}} dp(v)=count(son(v))+max{dp(son(v))}

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    List<Integer>[] tree;

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), v;
        tree = new List[n + 1];
        for (int w = 2; w <= n; w++) {
            v = in.readInt();
            if (tree[v] == null)
                tree[v] = new ArrayList();
            tree[v].add(w);
        }
        System.out.println(dp(1));
    }

    int dp(int v) {
        if (tree[v] == null) return 0;
        int max = 0;
        for (int w : tree[v])
            max = Math.max(max, dp(w));
        return tree[v].size() +  max;
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

#H exclusive or sequence

time limit: 2.0 2.0 2.0s memory limit: 512.0 512.0 512.0MB total score of this question: 20 20 20 points

   A l i c e \mathrm{Alice} Alice and B o b \mathrm{Bob} Bob is playing a game of XOR sequence. Initially, A l i c e \mathrm{Alice} Alice and B o b \mathrm{Bob} Bob has an integer respectively a a a and b b b. There is a given length of n n Common sequence of n X 1 , X 2 , ⋯   , X n X_1, X_2, \cdots , X_n X1​,X2​,⋯,Xn​.
   A l i c e \mathrm{Alice} Alice and B o b \mathrm{Bob} Bob takes turns, A l i c e \mathrm{Alice} Alice takes the lead. You can choose one of the following two options for each step:
  options 1 1 1: Choose one from the sequence X i X_i Xi # give A l i c e \mathrm{Alice} Alice's number XOR, or order a a a becomes a ⊕ X i a ⊕ X_i a⊕Xi​. (among them) ⊕ ⊕ ⊕ indicates bitwise XOR)
  options 2 2 2: Choose one from the sequence X i X_i Xi # give B o b \mathrm{Bob} Bob's number XOR, or order b b b becomes b ⊕ X i b ⊕ X_i b⊕Xi​.
  each number X i X_i Xi can only be used once when all X i X_i Xi # after being used( n n (after n rounds) the game is over. At the end of the game, the party with a larger number wins. If the two sides have the same number, it is a tie.
  now both sides are smart enough to adopt the best strategy. Who can win?

Input format

  each evaluation case contains multiple sets of queries. Inquiries are independent of each other.
  the first line of input contains an integer T T T. Indicates the number of queries.
  next T T Line T each line contains a set of queries. Among them i i The first integer of line i n i n_i ni represents the length of the sequence, and then n i n_i ni is an integer X 1 , X 2 , ⋯   , X n i X_1, X_2, \cdots , X_{ni} X1, X2,..., Xni represent each number in the sequence.

Output format

  output T T Line T, corresponding to the answers of each group in turn.
  each line contains an integer 1 1 1, 0 0 0 or − 1 −1 − 1 respectively indicates A l i c e \mathrm{Alice} Alice wins, draws or loses.

Test example 1

Input: 
4
1 1
1 0
2 2 1
7 992438 1006399 781139 985280 4729 872779 563580

Output: 
1
0
1
1

Scale and agreement of evaluation cases

  for all evaluation cases, 1 ≤ T ≤ 200000 1 \leq T \leq 200000 1≤T≤200000， 1 ≤ ∑ i = 1 T n i ≤ 200000 1 \leq \sum_{i=1}^T n_i \leq 200000 1≤∑i=1T​ni​≤200000， 0 ≤ X i < 2 20 0 \leq X_i < 2^{20} 0≤Xi​<220.

To be done

#I bidirectional sorting

time limit: 5.0 5.0 5.0s memory limit: 512.0 512.0 512.0MB total score of this question: 25 25 25 points

Problem description

  given sequence ( a 1 , a 2 , ⋅ ⋅ ⋅ , a n ) = ( 1 , 2 , ⋅ ⋅ ⋅ , n ) (a_{1}, a_{2}, · · · , a_{n}) = (1, 2, · · · , n) ½½½½½, i.e.,½½, ½½, ½½, ½½, ½½, ½½ a i = i a_{i} = i ai​=i.
  Xiaolan will test this sequence m m m operations, each time may be a 1 , a 2 , ⋅ ⋅ ⋅ , a q i a_{1}, a_{2}, · · · , a_{q_{i}} a1, a2, ⋅⋅⋅⋅, aqi are arranged in descending order, or a q i , a q i + 1 , ⋅ ⋅ ⋅ , a n a_{q_{i}}, a_{q_{i+1}}, · · · , a_{n} aqi, aqi+1, ⋅⋅⋅, an ⋅ in ascending order.
  request the sequence after the operation is completed.

Input format

  the first line of input contains two integers n , m n, m n. M, respectively represents the length of the sequence and the number of operations.
  next m m Line m describes the operation on the sequence, where i i Line i contains two integers p i , q i p_{i}, q_{i} pi and qi denote the operation type and parameters. When p i = 0 p_{i} = 0 When pi = 0, it means that a 1 , a 2 , ⋅ ⋅ ⋅ , a q i a_{1}, a_{2}, · · · , a_{q_{i}} a1, a2, ⋅⋅⋅⋅, aqi in descending order; When p i = 1 p_{i} = 1 When pi = 1, it means that a q i , a q i + 1 , ⋅ ⋅ ⋅ , a n a_{q_{i}}, a_{q_{i+1}}, · · · , a_{n} aqi, aqi+1, ⋅⋅⋅, an ⋅ in ascending order.

Output format

   output a line containing n n n integers. Adjacent integers are separated by a space, indicating the sequence after the operation is completed.

Test example 1

Input: 
3 3
0 3
1 2
0 2

Output: 
3 1 2

Explanation: 
The original sequence is (1, 2, 3). 
After step 1 (3, 2, 1). 
After step 2 (3, 1, 2). 
After step 3 (3, 1, 2). The same as after step 2, because the first two numbers are in descending order.

Scale and agreement of evaluation cases

  for 30 30 30% of the evaluation cases, n , m ≤ 1000 n, m ≤ 1000 n,m≤1000；
  for 60 60 60% of the evaluation cases, n , m ≤ 5000 n, m ≤ 5000 n,m≤5000；
  for all evaluation cases, 1 ≤ n , m ≤ 100000 1 ≤ n, m ≤ 100000 1≤n,m≤100000， 0 ≤ p i ≤ 1 0 ≤ p_{i} ≤ 1 0≤pi​≤1， 1 ≤ q i ≤ n 1 ≤ q_{i} ≤ n 1≤qi​≤n；

De redundant operation

   in fact, if you see this data scale, you can write Brute Force in five minutes, and then you can go next, O ( m n log ⁡ n ) O(mn \log n) O(mnlogn) can pass 60 60 60% of use cases,

More time to prove the correctness of other procedures may lead to higher profits.

   however, just cheat two more points.

  for continuous and p i p_{i} pi ， same operation, in p i = 0 p_{i} = 0 When pi = 0, you only need to do q i q_{i} qi maximum operation, in p i = 1 p_{i} = 1 When pi = 1, you only need to do q i q_{i} qi) minimum operation, as shown in the figure:

   obviously, after removing the redundant operation, it is still equivalent to the original operation. It only needs to establish a stack to complete the redundancy removal in linear time, and the amount of code is less.

  in particular, I can first ( p : 1 , q : 1 ) (p:1,q:1) (p:1,q:1) press into the bottom of the stack.

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.readInt(), m = in.readInt();
        Deque<Step> deque = new ArrayDeque();
        deque.push(new Step(1, 1));
        while (m-- > 0) {
            int p = in.readInt();
            int q = in.readInt();
            while (deque.size() > 0 && deque.peek().p == p)
                if (p == 0)
                    q = max(q, deque.pop().q);
                else
                    q = min(q, deque.pop().q);
            deque.push(new Step(p, q));
        }
        Integer[] ans = new Integer[n];
        for (int i = 0; i < n; i++)
            ans[i] = i + 1;
        deque.pollLast();
        while (deque.size() > 0) {
            Step step = deque.pollLast();
            if (step.p == 0)
                Arrays.sort(ans, 0, step.q, (a, b)->(b - a));
            else
                Arrays.sort(ans, step.q - 1, n);
        }
        for (int i = 0; i < n; i++) {
            out.print(ans[i]);
            out.print(' ');
        }
        out.flush();
    }

    int max(int a, int b) { return a > b ? a : b; }

    int min(int a, int b) { return a < b ? a : b; }

    class Step {

        int p, q;

        Step(int p, int q) {
            this.p = p;
            this.q = q;
        }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

Figure filling game

  in fact, I wanted to write directly to this step at the beginning,

  but I'm busy and a little free at the same time. Let's open it and write it.

   after the above redundancy removal operation, it can be found that the last thing to be operated is a p   0 ∣ 1 p \ 0\mid 1 p ∣ 0 ∣ 1 alternating sequence, in order to facilitate readers' understanding,

   here, the original sequence and operation are abstracted into unequal length and different color line segments,

  special, original sequence and p = 1 p = 1 The operation of p=1 is a color, because the original sequence is in ascending order.

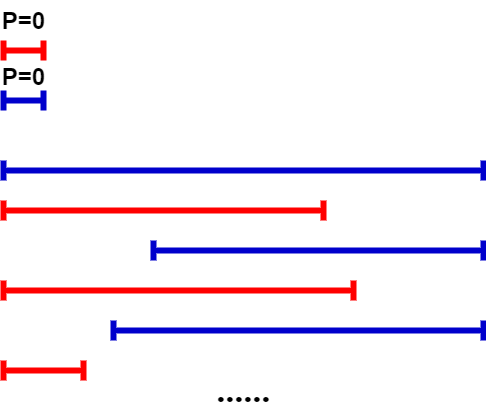
  will p = 0 p=0 p=0 and p = 1 p=1 p=1 maximum operating range is marked.

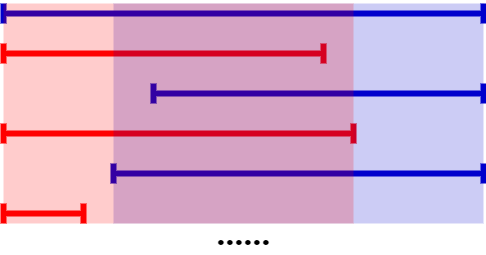
  obviously, in q q When q is not the endpoint, each operation has a constant interval.

  the image tells us that if q q The scope of q operation exceeds the nearest one in the stack q q q. So not only this recent q q q. Together with the top of the stack q q q the opposite operations can be skipped.

   at the same time, after optimization according to this property, we can always find an invariant interval in forward or reverse order according to the remaining operations in the stack.

   fill the invariant interval into the final answer, and the whole algorithm is basically completed.

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.readInt(), m = in.readInt(), top;
        Step[] stack = new Step[m + 1];
        for (top = 0; m-- > 0;) {
            int p = in.readInt();
            int q = in.readInt();
            if (p == 0) {
                while (top > 0 && stack[top].p == p) q = max(q, stack[top--].q);
                while (top > 1 && stack[top - 1].q <= q) top -= 2;
                stack[++top] = new Step(p, q);
            } else if (top > 0){
                while (top > 0 && stack[top].p == p) q = min(q, stack[top--].q);
                while (top > 1 && stack[top - 1].q >= q) top -= 2;
                stack[++top] = new Step(p, q);
            }
        }
        int[] ans = new int[n + 1];
        int a = n, l = 0, r = n - 1;
        for (int i = 1; i <= top; i++)
            if (stack[i].p == 0)
                while (r >= stack[i].q && l <= r) ans[r--] = a--;
            else
                while (l + 1 < stack[i].q && l <= r) ans[l++] = a--;
        if ((top & 1) == 1)
            while (l <= r) ans[l++] = a--;
        else
            while (l <= r) ans[r--] = a--;
        for (int i = 0; i < n; i++) {
            out.print(ans[i]);
            out.print(' ');
        }
        out.flush();
    }

    int max(int a, int b) { return a > b ? a : b; }

    int min(int a, int b) { return a < b ? a : b; }

    class Step {

        int p, q;

        Step(int p, int q) {
            this.p = p;
            this.q = q;
        }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

Chtholly Tree

  unlimited Kodori tree( C h t h o l l y T r e e \mathrm{Chtholly Tree} Chthallytree) is a value domain line segment tree built on the red black tree. Under the randomly constructed data, the expected complexity is O ( n log ⁡ log ⁡ n ) O(n \log \log n) O(nloglogn)，

  but J a v a \mathrm{Java} Java implementation is very painful, so p l a n   B \mathrm{plan\ B} plan B, using linked list instead,

  the expected complexity under the randomly constructed data is O ( n log ⁡ n ) O(n \log n) O(nlogn).

The strategy of   Kodori tree is to merge the intervals with the same value range into one node,

  for any [ L , R ] [L,R] We can all convert the operations on [L,R] into a Kodori tree m e r g e ( s p l i t ( L ) , s p l i t ( R + 1 ) ) \mathrm{merge(split(L), split(R+1))} Operation on merge(split(L),split(R+1)).

  this is actually a Kodori list, not a tree

  it's still too difficult for me to give a concrete and vivid example,

  brothers, please find a blog for reference.

  although it's simple to pinch and kick the data of the cortoria tree,

  but in terms of the difficulty of blue bridge,

  it's still a question whether the author has seen it or not.

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), m = in.readInt();
        Node[] root = new Node[n + 1];
        int[] P = new int[n + 1];
        Range lower, temp, now;
        lower = now = new Range(0);
        for (int i = 1; i <= n; i++) {
            now = now.next = new Range(i);
            root[i] = build(1, n, i);
        }
        now.next = new Range(n + 1);
        while (m-- > 0) {
            int p = in.readInt();
            int L = in.readInt();
            int R = n;
            if (p == 0) {
                R = L;
                L = 1;
            }
            now = lower;
            while (now.next.L <= L) now = now.next;
            if (L > now.L) {
                root[L] = split(root[now.L], L - now.L, P[now.L]);
                now = now.next = new Range(L, now.next);
            }
            temp = now;
            Node pq = null;
            while (now.L <= R) {
                if (now.next.L > R + 1) root[R + 1] = split(root[now.L], R + 1 - now.L, P[R + 1] = P[now.L]);
                pq = merge(pq, root[now.L]);
                now = now.next;
            }
            if (now.L == R + 1) temp.next = now;
            else temp.next = new Range(R + 1, now);
            root[L] = pq;
            P[L] = p;
        }
        StringBuilder ans = new StringBuilder();
        while ((lower = lower.next).L <= n)
            buildAns(ans, root[lower.L], 1, n, P[lower.L]);
        System.out.println(ans);
    }

    Node split(Node tree, int k, int p) {
        if (tree == null) return null;
        Node split= new Node(0);
        if (p == 0) {
            int K = K(tree.right);
            if (k <= K) {
                if (k != K) split.right = split(tree.right, k, p);
                split.left = tree.left;
                tree.left = null;
            } else split.left = split(tree.left, k - K, p);
        } else {
            int K = K(tree.left);
            if (k <= K) {
                if (k != K) split.left = split(tree.left, k, p);
                split.right = tree.right;
                tree.right = null;
            } else split.right = split(tree.right, k - K, p);
        }
        split.k = tree.k - k;
        tree.k = k;
        return split;
    }

    Node merge(Node tree1, Node tree2) {
        if (tree1 == null) return tree2;
        if (tree2 != null){
            tree1.k += K(tree2);
            tree1.left = merge(tree1.left, tree2.left);
            tree1.right = merge(tree1.right, tree2.right);
        }
        return tree1;
    }

    Node build(int L, int R, int k) {
        if (L == R) return new Node(1);
        Node node = new Node(1);
        int mid = L + R >> 1;
        if (k <= mid) node.left = build(L, mid, k);
        else node.right = build(mid + 1, R, k);
        return node;
    }

    void buildAns(StringBuilder builder, Node root, int L, int R, int p) {
        if (root == null) return;
        if (L == R) builder.append(L).append(' ');
        else {
            int mid = L + R >> 1;
            if (p == 0) {
                buildAns(builder, root.right, mid + 1, R, p);
                buildAns(builder, root.left, L, mid, p);
            } else {
                buildAns(builder, root.left, L, mid, p);
                buildAns(builder, root.right, mid + 1, R, p);
            }
        }
    }

    int K(Node node) { return node == null ? 0 : node.k; }

    class Range {

        int L;

        Range next;

        Range(int L) { this(L, null); }

        Range(int L, Range next) {
            this.L = L;
            this.next = next;
        }
    }

    class Node {

        int k = 1;

        Node left, right;

        Node(int k) { this.k = k; }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) { this.reader = new BufferedReader(new InputStreamReader(in)); }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(this.read()); }
    }
}

#J sub fruit

time limit: 10.0 10.0 10.0s memory limit: 512.0 512.0 512.0MB total score of this question: 25 25 25 points

Problem description

  Xiao Lan is going to be at her birthday party n n n packets of candy m m m children. Each package of candy should be distributed. Each child should be divided into at least one package or more packages.
   Xiaolan has prepared the candy in advance. In order to divide the candy more evenly on the day of the banquet, Xiaolan must first calculate the distribution plan.
  little blue took the candy from 1 1 1 to n n n number, page i i i package candy weight w i w_i wi​. Children from 1 1 1 to m m m number. Each child can only get candy with consecutive numbers. Xiaolan thought for a long time and didn't come up with an appropriate distribution plan, so that each child's candy was almost heavy. So you need to help him find a way together. In order to better distribute candy, he can buy some more candy and make two copies of some numbered candy. When there are two pieces of candy with a certain number, a child can only share one of them at most.
   please find a plan to minimize the difference between the maximum weight and the minimum weight of candy distributed by children. Please output this difference.
  for example, Xiaolan now has 5 5 5 bags of candy, weighing 6 , 1 , 2 , 7 , 9 6, 1, 2, 7, 9 6,1,2,7,9. If Xiaolan wants to share it with two children, he can buy another copy of all the candy and both children will share it 1 1 1 to 5 5 Five packs of candy, all weighing 25 25 25, the difference is 0 0 0.
  for another example, Xiaolan has 5 5 5 bags of candy, weighing 6 , 1 , 2 , 7 , 9 6, 1, 2, 7, 9 6,1,2,7,9. If Xiaolan wants to give three children, he can give the third child 3 3 Buy another three packs of candy and the first child will share it 1 1 1 to 3 3 Three children, three children 3 3 3 to 4 4 Four bags, the third child is divided into three 5 5 5 bags. Each child is given a weight of 9 9 9. The difference is 0 0 0.
  for another example, Xiaolan has 5 5 5 bags of candy, weighing 6 , 1 , 2 , 7 , 9 6, 1, 2, 7, 9 6, 1, 2, 7, 9. If Xiao Lan wants to give it to four children, he can give it to the third child 3 3 Package 3 and section 3 5 5 If you buy another five packs of candy, you can still share the weight of each child 9 9 9. The difference is 0 0 0.
  for another example, Xiaolan has 5 5 5 bags of candy, weighing 6 , 1 , 2 , 7 , 9 6, 1, 2, 7, 9 6,1,2,7,9. If Xiaolan wants to give five children, he can give the third child 4 4 Package 4 and 5 5 Buy another five packs of candy, and the first child will share the second 1 1 1 to 2 2 2 packages weighing 7 7 7. The second child is divided into two groups 3 3 3 to 4 4 4 packages weighing 9 9 9. The third child is divided into three groups 4 4 4 packages weighing 7 7 7. The fourth and fifth children are divided into the third 5 5 5 packages weighing 9 9 9. Difference is 2 2 2.

Input format

  the first line of input contains two integers n n n and m m m. It indicates the number of candy bags and the number of children respectively.
  the second line contains n n n integers w 1 , w 2 , ⋅ ⋅ ⋅ , w n w_1, w_2, · · · , w_n w1, w2, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅.

Output format

   output an integer indicating the difference between the maximum weight and the minimum weight of candy distributed by children under the optimal condition.

Test example 1

Input: 
5 2
6 1 2 7 9

Output: 
0

Test example 2

Input: 
5 5
6 1 2 7 9

Output: 
2

Scale and agreement of evaluation cases

  for 30 30 30% of the evaluation cases, 1 ≤ n ≤ 10 1 \leq n \leq 10 1≤n≤10， 1 ≤ m ≤ 10 1 \leq m \leq 10 1≤m≤10， 1 ≤ w i ≤ 10 1 \leq w_i \leq 10 1≤wi​≤10；
  for 60 60 60% of the evaluation cases, 1 ≤ n ≤ 30 1 \leq n \leq 30 1≤n≤30， 1 ≤ m ≤ 20 1 \leq m \leq 20 1≤m≤20， 1 ≤ w i ≤ 30 1 \leq w_i \leq 30 1≤wi​≤30；
  for all evaluation cases, 1 ≤ n ≤ 100 1 \leq n \leq 100 1≤n≤100， 1 ≤ m ≤ 50 1 \leq m \leq 50 1≤m≤50， 1 ≤ w i ≤ 100 1 \leq w_i \leq 100 1≤wi​≤100. In the evaluation data, w i w_i wi# randomly generated and evenly distributed in a certain interval.

To be done