Sword finger Offer 30 Stack containing min function

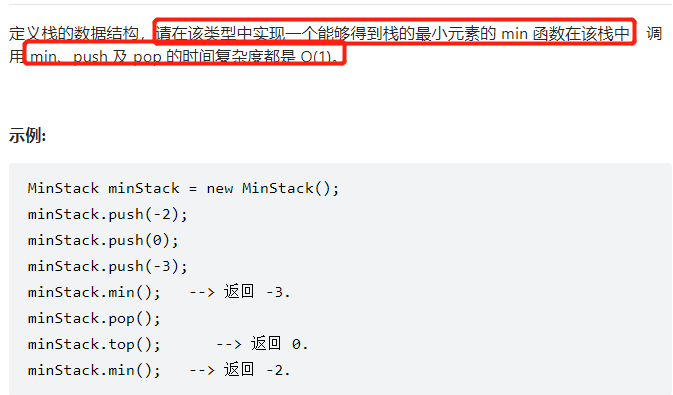
Use the auxiliary value s2 to store the minimum value. If there is one smaller than s2, let the smaller value enter s2. When the minimum value in the original s1 comes out of the stack, judge that if it is equivalent to the s2 value, it means that the minimum value needs to be updated, then the s2 stack pushes out of the stack

class MinStack {
public:
    stack<int>s1;
    stack<int>s2;
    
    /** initialize your data structure here. */
    MinStack() {
        s2.push(INT_MAX);
    }
    
    void push(int x) {
        s1.push(x);
        if(x<=s2.top()){	
            s2.push(x);
        }
    }
    void pop() {
        if(s1.top()==s2.top())  s2.pop(); //s1 out of stack element is equal to the minimum value saved at the top of s2 stack
        s1.pop();        
    }
    int top() {
        return s1.top();
    }   
    int min() {
        return s2.top();	//The stack top of s2 always keeps the minimum value
    }
};

Interview question 32 - I. print binary tree from top to bottom

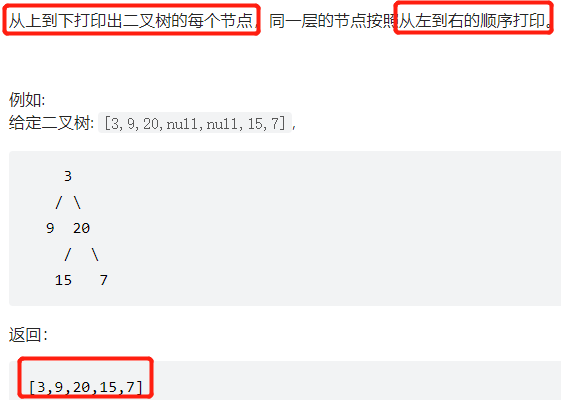
The hierarchical traversal of binary tree 3, 9, 20, 15 and 7 join the team in turn

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int>v;
        if(root == NULL)    return v;
        queue<TreeNode*>q;	//Initialize queue
        q.push(root);	    //Root node join
        while(!q.empty()){
            TreeNode * node = q.front();	//Team first team
            q.pop();
            v.push_back(node->val);			
            if(node->left)  q.push(node->left);		//The left child of this node joins the team
            if(node->right)  q.push(node->right);	//Right child joins the team
        }
        return v;
    }
};

Sword finger Offer 32 - II Print binary tree II from top to bottom

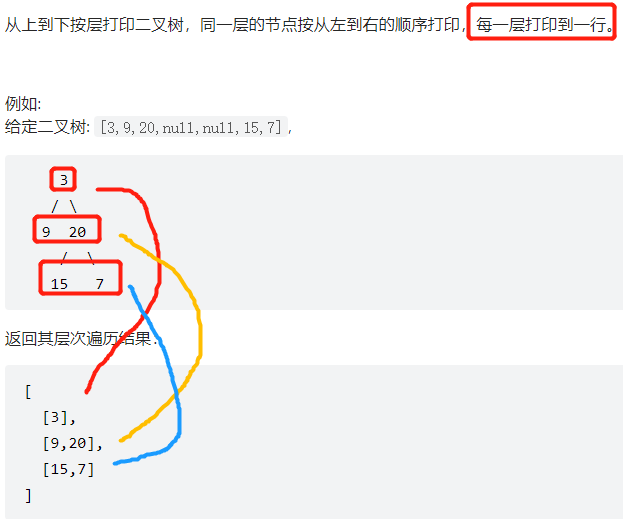
It is almost as like as two peas. It is more stratified output. How to divide into groups: root node joining, queue size() 1, root node children joining the team, queue size() 2, assuming two full tree, then down, size() 4. All the time, there are several nodes in each layer, i=q.size(), and then i -- output each node

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // Hierarchical traversal problem
        vector<vector<int>> v;
        if(root==NULL){
            return v;
        }
        queue<TreeNode *>q;
        q.push(root);
        while(!q.empty()){	//When the queue is not empty
        vector<int>temp;
            for(int i=q.size();i>0;i--)	//Key layered approach
            {
                TreeNode * node = q.front();
                q.pop();
                temp.push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            v.push_back(temp);	//Save the results of this layer
        }
        return v;
    }
};

Sword finger Offer 32 - III. print binary tree III from top to bottom![image-20220306113134809]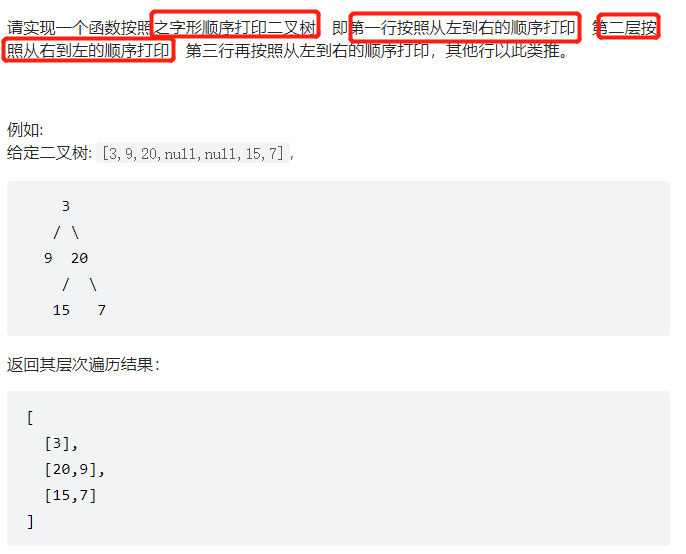

Method 1: the same as the previous question, but use a number to record the number of layers, and then the odd layers are normal, and the even layers can be reversed

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // Hierarchical traversal problem
        vector<vector<int>> v;
        if(root==NULL){
            return v;
        }
        queue<TreeNode *>q;
        q.push(root);
        int deep = 1;
        while(!q.empty()){//When the queue is not empty
        vector<int>temp;
        
            for(int i=q.size();i>0;i--)//Key layered approach
            {
                TreeNode * node = q.front();
                q.pop();
                temp.push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            if(deep%2 ==0){
                reverse(temp.begin(),temp.end());
            }
            v.push_back(temp);
            deep++;
        }
        return v;
    }
};

Double ended queues can also be used

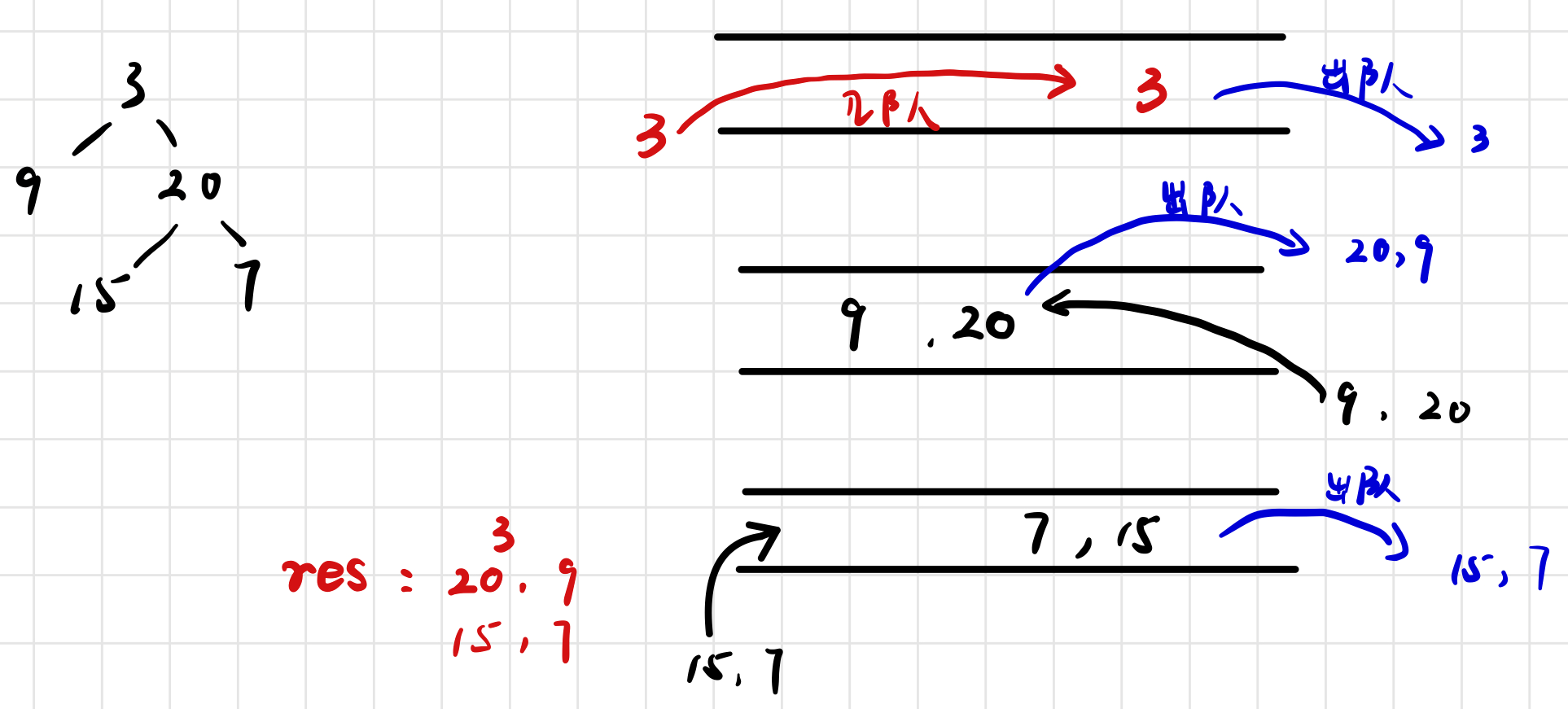
// Use double ended queue (even layer of tree): tail in (first left child node and then right child node) and head out; Odd layer of tree: head in (first right child node and then left child node) tail out)
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }

        vector<vector<int>> vec;
        deque<TreeNode*>dqe;           

        int level = 0;
        dqe.push_back(root);                   // The root node is in layer 0 (even layer), so it enters from the end of the queue
        while (!dqe.empty()) {
            int level_nodes = dqe.size();
            vec.push_back({});

            if (level % 2 != 0) {              // Odd layer: enter from the head of the queue (first the right child node and then the left child node), and exit from the end of the queue
                while (level_nodes) {
                    TreeNode* p_node = dqe.back();
                    if (p_node->right != nullptr) dqe.push_front(p_node->right);
                    if (p_node->left != nullptr) dqe.push_front(p_node->left);

                    vec[level].push_back(p_node->val);
                    dqe.pop_back();
                    --level_nodes;
                }
                ++level;
            }
            else {                             // Even layer: enter from the end of the queue (first the left child node and then the right child node), and exit from the head of the queue
                while (level_nodes) {
                    TreeNode* p_node = dqe.front();
                    if (p_node->left != nullptr) dqe.push_back(p_node->left);
                    if (p_node->right != nullptr) dqe.push_back(p_node->right);

                    vec[level].push_back(p_node->val);
                    dqe.pop_front();
                    --level_nodes;
                }
                ++level;
            }
        }

        return vec;
    }
};

88. Merge two ordered arrays

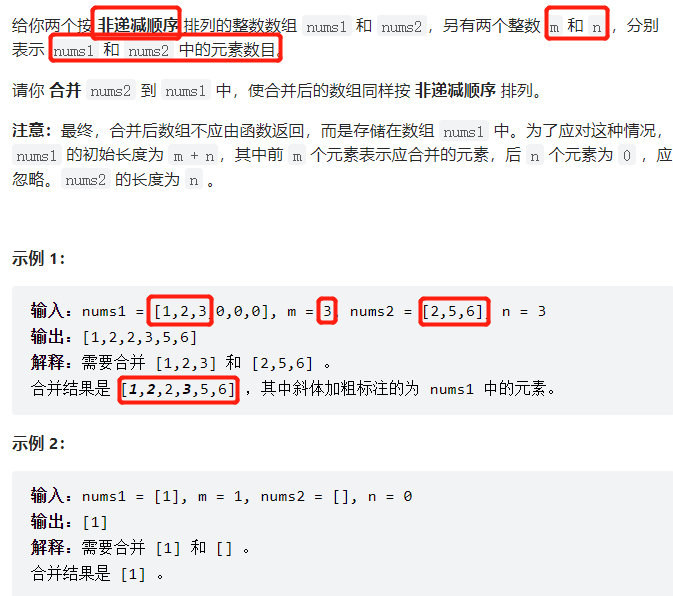
That is, give two non decreasing arrays, and then let you combine the first n bits of the first array and the first m bits of the second array into one array 1 (the length of array 1 is M+N)

Reverse order double pointer (the idea of double pointer is commonly used)

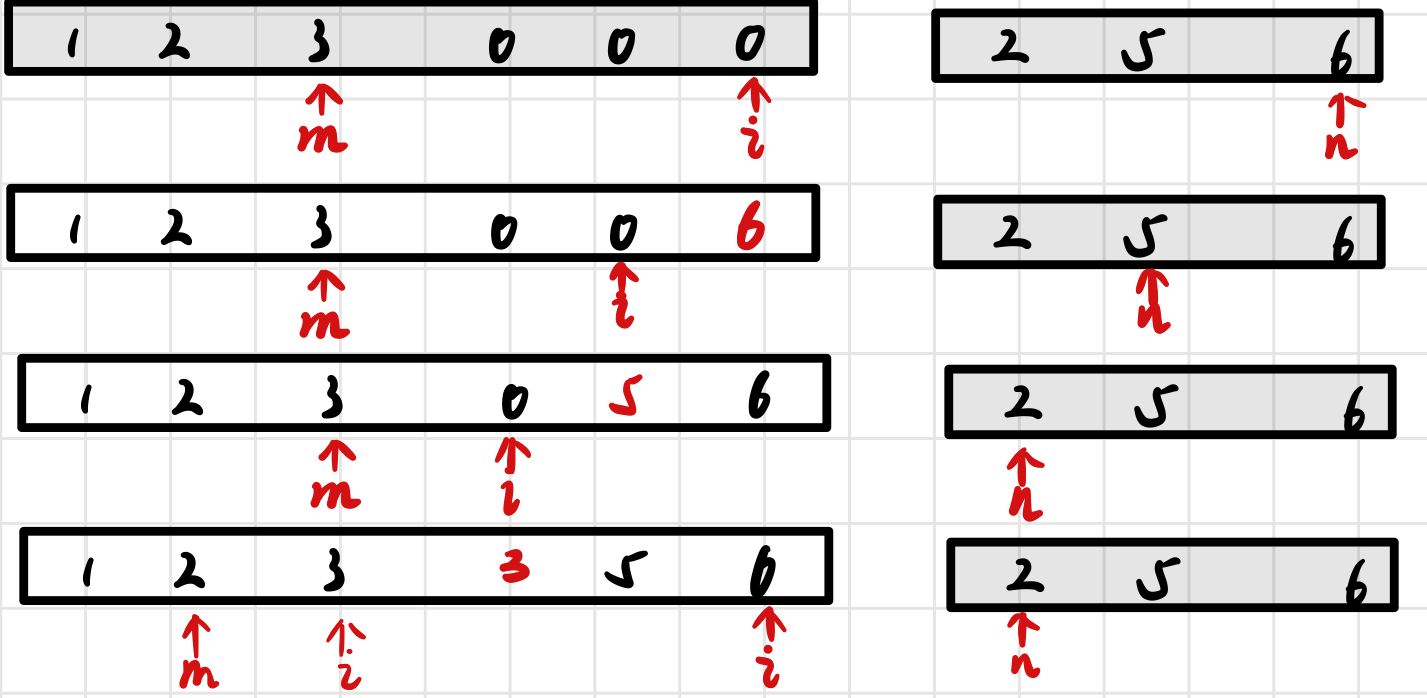
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int i = nums1.size() - 1;
    m--;	 //The subscript starts at 0, so subtract 1 first
    n--;
    while (n >= 0) {
        while (m >= 0 && nums1[m] > nums2[n]) {
            nums1[i--]=nums1[m--];
        }
        nums1[i--]=nums2[n--];
    }
}

Sword finger Offer 39 A number that appears more than half the time in the array

This question is the original question that appeared in 408. The best thing to think of is to make statistics and sort, but this question uses the voting method

Because the mode must appear. Every time the mode appears, it will be + 1, not - 1. Finally, it must be greater than 0

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int res = nums[0];	//Let nums[0] be the mode first
        int count = 1;
        for(int i = 1;i<nums.size();i++){
            if(nums[i]==res){	//Equal value++
                count++;
            }else{	//Further judgment of unequal values
                if(count==1){	//If there is only one time left, update the mode
                    res = nums[i];
                }else{
                    count--;	//Number of occurrences--
                }
            }
        }
        return res;
    }
};

The writing method of the boss: this question has particularity, that is, it is not necessary to judge whether it is a mode. It is best to add a judgment

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x = 0, votes = 0, count = 0;
        for(int num : nums){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        // Verify that x is mode
        for(int num : nums)
            if(num == x) count++;
        return count > nums.size() / 2 ? x : 0; // Returns 0 when there is no mode
    }
};

Sword finger Offer 40 Minimum number of k

Four solutions to spike TopK (fast row / heap / binary search tree / count sort) ❤️ - Minimum k number - LeetCode (LeetCode CN. Com)

Sword finger Offer 40 Minimum number of k (array division based on quick sorting, clear illustration) - minimum number of k - LeetCode (leetcode-cn.com)

1. Fast selection algorithm

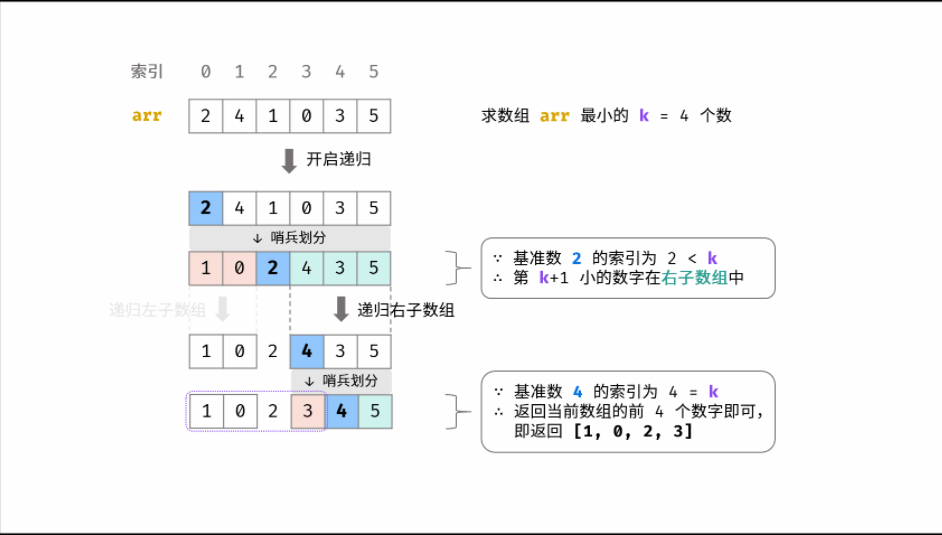
Optimized quick sort, because you only need to find the smallest k, and don't care about their order

As with the fast platoon, it is used frequently

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {

        if(k>=arr.size())    return arr;
        return quick_select(arr, k, 0, arr.size() - 1);
    }
    vector<int>quick_select(vector<int>&arr,int k,int low,int high){
        int i = low;
        int j = high;
        int pivot = arr[i];//Select pivot
        while(i<j){
            while(i<j && arr[j]>=pivot)  --j;
            arr[i] = arr[j] ;
            while(i<j && arr[i]<=pivot)  ++i;
            arr[j] = arr[i];
        }
        arr[i] = pivot;    //Pivot return
        // Then judge whether to continue. If I > k, the range is large and the range is reduced
        //If I < K represents that our scope is small, it needs to be divided again
        if (i > k) return quick_select(arr, k, low, i - 1);
        if (i < k) return quick_select(arr, k, i + 1, high);
        vector<int> res;
        res.assign(arr.begin(), arr.begin() + k);   //Return to the first K
        return res;
    }
};

414. The third largest number

Method 1: use the set (default sorting) and save only 3 numbers

class Solution {
public:
    int thirdMax(vector<int> &nums) {
        set<int> s;
        for (int num : nums) {
            s.insert(num);
            if (s.size() > 3) {	//If there are more than 3 elements, delete the smallest one
                s.erase(s.begin());
            }
        }
        return s.size() == 3 ? *s.begin() : *s.rbegin();	//If the number is less than 3, the maximum number will be returned (in the case of example 2)
    }
};

Solution 2: with three pointers, you can find it with only one round of scanning

class Solution {
public:
    int thirdMax(vector<int> &nums) {
        int *a = nullptr, *b = nullptr, *c = nullptr;
        for (int &num : nums) {
            if (a == nullptr || num > *a) {
                c = b;
                b = a;
                a = &num;
            } else if (*a > num && (b == nullptr || num > *b)) {
                c = b;
                b = &num;
            } else if (b != nullptr && *b > num && (c == nullptr || num > *c)) {
                c = &num;
            }
        }
        return c == nullptr ? *a : *c;
    }
};

215. The kth largest element in the array (this condition is more stringent than the above)

Solution 1: direct fast platoon

Solution 2: quick selection

class Solution {
public:
    int quickSelect(vector<int>& a, int l, int r, int index) {
        int q = randomPartition(a, l, r);
        if (q == index) {
            return a[q];
        } else {
            return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
        }
    }
    inline int randomPartition(vector<int>& a, int l, int r) {
        int i = rand() % (r - l + 1) + l;//Introduce randomization 	 The time complexity of fast scheduling depends on the partition
        swap(a[i], a[r]);
        return partition(a, l, r);
    }
    inline int partition(vector<int>& a, int l, int r) {//divide
        int x = a[r], i = l - 1;
        for (int j = l; j < r; ++j) {
            if (a[j] <= x) {
                swap(a[++i], a[j]);
            }
        }
        swap(a[i + 1], a[r]);
        return i + 1;
    }
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(0));
        return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
    }
};

Solution 3: using large root pile

class Solution {
public:
    void maxHeapify(vector<int>& a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a[i], a[largest]);
            maxHeapify(a, largest, heapSize);
        }
    }

​    void buildMaxHeap(vector<int>& a, int heapSize) {	//Reactor building operation
​        for (int i = heapSize / 2; i >= 0; --i) {
​            maxHeapify(a, i, heapSize);
​        } 
​    }

​    int findKthLargest(vector<int>& nums, int k) {
​        int heapSize = nums.size();
​        buildMaxHeap(nums, heapSize);
​        for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
​            swap(nums[0], nums[i]);
​            --heapSize;
​            maxHeapify(nums, 0, heapSize);
​        }
​        return nums[0];
​    }
};