Data structure - red black tree

preface

Red black tree is the underlying data structure of map, set, mutilmap and mutilset containers. It is also a very important data structure. It further optimizes AVL in efficiency, because AVL structure cannot avoid a large number of rotation operations during insertion or deletion, resulting in loss of efficiency. However, red black tree has been better optimized in this point, But at the expense of balance, it is not a fully balanced binary search tree.

1, Concept and properties of red black tree

Concept:

Red Black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node, which can be red or Black. By limiting the coloring mode of each node on any path from root to leaf, the red Black tree ensures that no path will be twice longer than other paths, so it is close to balance.

nature:
1. The root node is black

2. Each node is either red or black

3. The child nodes of red nodes must be black

4. Red nodes cannot be connected

5. Starting from any node, the number of black nodes on each path is the same

Here is a doggerel summarizing the red and black trees:

One head and one foot are black,
Black and red.
Look at your uncle,
Delete watch brother.

These four sentences summarize all the properties of red black trees and how to deal with them when inserting and deleting them.

2, Definition of red black tree node

#include<iostream>
#include<stack>
#include<vector>
using namespace std;
enum Color{BLACK = 0,RED = 1};  //Set color

template<typename Type>    //Class, otherwise there may be an error when declaring a friend class due to the compiler version
class RBTree;

template<typename Type>
class RBTreeNode
{
	friend class RBTree<Type>;   //Become a friend class that can access private members of the node
public:
	RBTreeNode(Type val = Type())
		:_rightChild(nullptr),_leftChild(nullptr),_parent(nullptr),_Val(val),_color(RED)
	{}
	~RBTreeNode()
	{}
private:
	Type _Val;
	RBTreeNode<Type>* _rightChild;
	RBTreeNode<Type>* _leftChild;
	RBTreeNode<Type>* _parent;
	Color _color;
};

template<typename Type>
class RBTree
{
public:
	RBTree():Nul(_BuyNode()),_root(Nul)
	{
		Nul->_leftChild = Nul->_rightChild = Nul->_parent = nullptr;
		Nul->_color = BLACK;
	}
protected:
	RBTreeNode<Type>* _BuyNode(const Type val = Type())  
	{
		RBTreeNode<Type>* s = new RBTreeNode<Type>(val);
		s->_leftChild = s->_rightChild = Nul;
		return s;
	}
private:
	RBTreeNode<Type>* Nul;
	RBTreeNode<Type>* _root;
};

We have two classes, one is our red black tree class, the other is the leaf node class
Red and black trees:
There are two members. Here is another man-made view of the red black tree, that is, all empty nodes are black nodes, and the root must be black nodes. Therefore, we can't have no root during initialization, and there must be a black node as the root node during initialization. Then why_ There is another node besides root as an empty node, and all empty nodes point to this node.

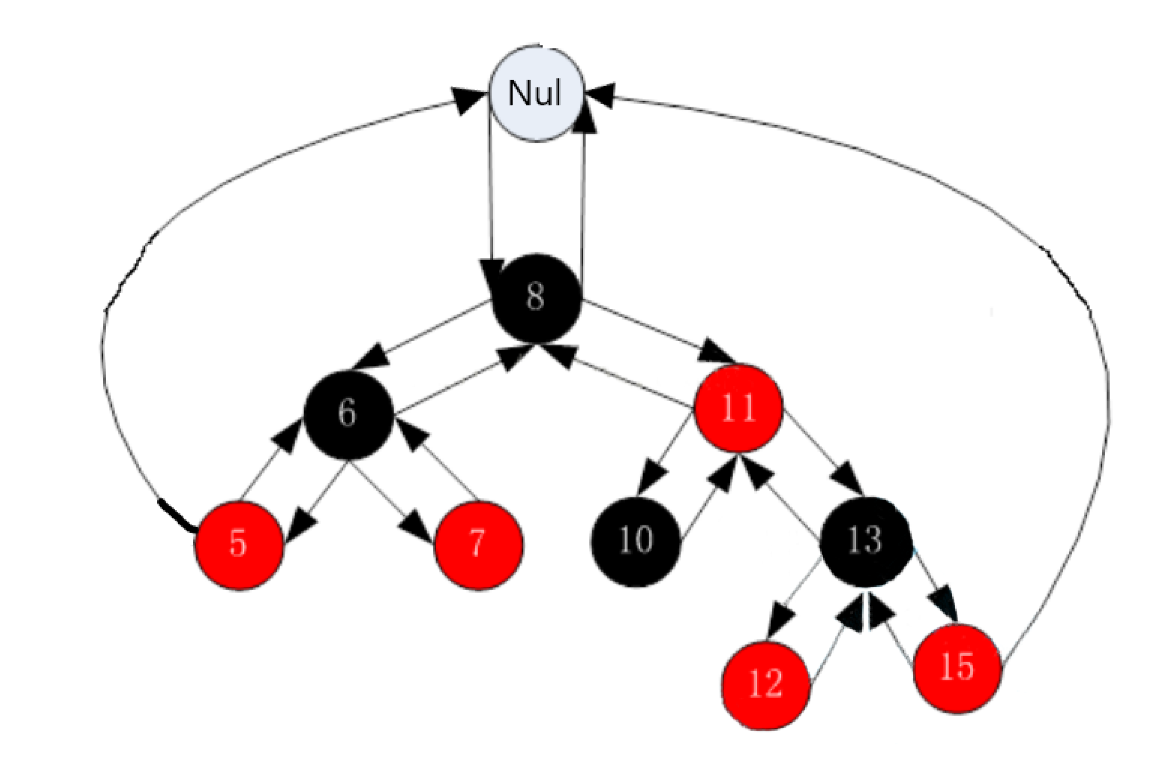
Then, for the convenience of adjustment, we use an extra parent pointer to point to our parent node, because without this, inserting and deleting will become super troublesome in the future! We'll talk about it later.

3, Rotation of red black tree

Here, we don't need to write four rotation methods like AVL tree. Because we are beginning to learn, we need to be more detailed. Now we directly choose to call left single rotation and right single rotation to realize double rotation at the same time, so we don't need to repeat the implementation. It improves the reusability of the code.

1. Right single rotation

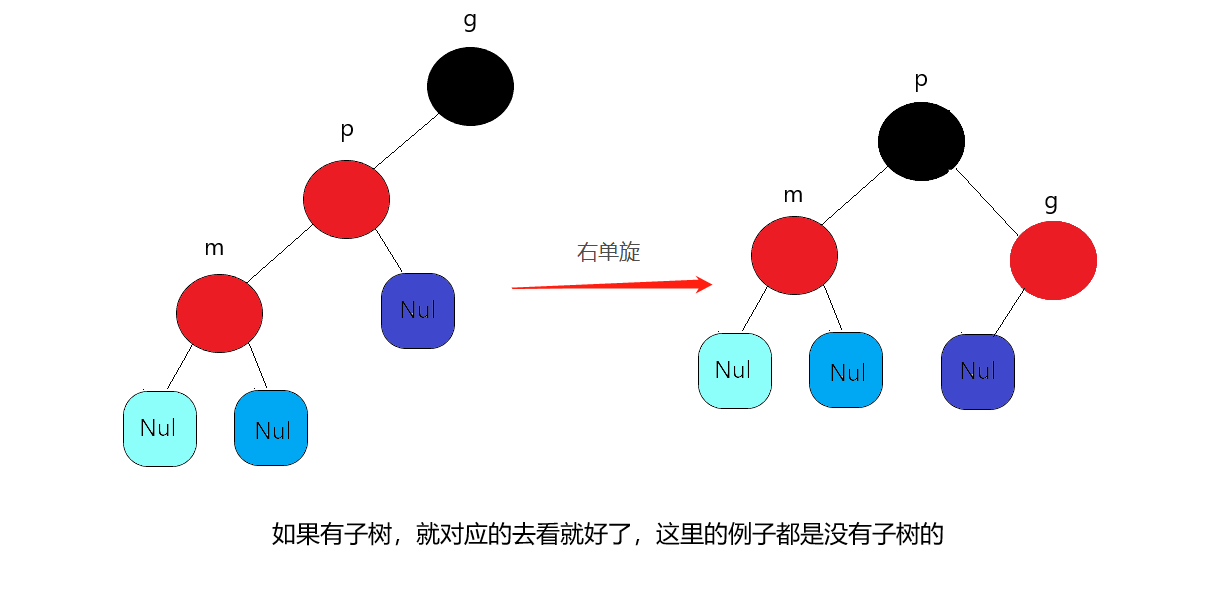
Because we have finished the color modification before the rotation, we only need to rotate

template<typename Type>
void RBTree<Type>::RotateR(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
	RBTreeNode<Type>* s = p->_leftChild;
	/*Judge whether there is a left subtree at the position to be rotated. If so, hang it on the right subtree of the node to be rotated in the future
	  secondly. If not, as mentioned at the beginning, the empty nodes of all nodes point to the empty node Nul set by ourselves,
	  So just let the right subtree of p point to it.*/
	if (s->_rightChild != Nul)
		s->_rightChild->_parent = p;
	p->_leftChild = s->_rightChild;
	s->_parent = p->_parent;
	
	if (p->_parent == Nul)   //The rotated node is the root node
		t = s;
	else if (p == p->_parent->_leftChild)  //If it is not the root node, judge whether it is the left subtree or the right subtree for connection
		p->_parent->_leftChild = s; 
	else
		p->_parent->_rightChild = s;
		
	s->_rightChild = p;   //Adjust the other pointers of the node to
	p->_parent = s;
}

Why is it different from AVL tree in using reference to pass the value to be rotated this time? We can know from the code that the connection is completed directly while rotating this time, and the meaning of the specific steps will be identified in the code, which is more convenient to look at.

2. Left single rotation

void RBTree<Type>::RotateL(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
	RBTreeNode<Type>* s = p->_rightChild;
	/*Judge whether there is a left subtree at the position to be rotated. If so, hang it on the right subtree of the node to be rotated in the future
	  secondly. If not, as mentioned at the beginning, the empty nodes of all nodes point to the empty node Nul set by ourselves,
	  So just let the right subtree of p point to it.*/
	if (s->_leftChild != Nul)
		s->_leftChild->_parent = p;
	p->_rightChild = s->_leftChild;
	s->_parent = p->_parent;
	
	if (p->_parent == Nul)  //The rotated node is the root node
		t = s;
	else if (p == p->_parent->_leftChild) //If it is not the root node, judge whether it is the left subtree or the right subtree for connection
		p->_parent->_leftChild = s;
	else
		p->_parent->_rightChild = s;
		
	s->_leftChild = p;  //Adjust the other pointers of the node to
	p->_parent = s;
}

4, Insertion of red black tree

template<typename Type>
void RBTree<Type>::_Insert(RBTreeNode<Type>* &t, const Type val)
{
	RBTreeNode<Type>* p = t;
	RBTreeNode<Type>* pr = Nul;
	while (p != Nul)    //Find insertion location
	{
		if (val == p->_Val)  //The same data is not accepted
			return;

		pr = p;

		if (val > p->_Val)
			p = p->_rightChild;
		else
			p = p->_leftChild;
	}

	p = _BuyNode(val);
	if (pr == Nul)  // The first root node is inserted
	{
		t = p;
		t->_parent = pr;
	}

	if (val > pr->_Val)
		pr->_rightChild = p;
	else
		pr->_leftChild = p;
	p->_parent = pr;

	/*Adjust balance*/
	In_balance(t, p);
}
template<typename Type>
void RBTree<Type>::In_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
	while (m->_parent->_color == RED)
	{
		RBTreeNode<Type>* u;   //uncle node
		if (m->_parent == m->_parent->_parent->_leftChild)   //Left branch
		{
			u = m->_parent->_parent->_rightChild;
			if (u->_color == RED)     //Status 3: uncle s are red nodes
			{
				m->_parent->_color = BLACK;
				m->_parent->_parent->_color = RED;
				u->_color = BLACK;
				m = m->_parent->_parent;
			}
			else    //Uncles are black nodes
			{
				if (m == m->_parent->_rightChild)  //Status II  
				{
					m = m->_parent;
					RotateL(t, m);
				}
				m->_parent->_color = BLACK;                  //Status one
				m->_parent->_parent->_color = RED;
				RotateR(t, m->_parent->_parent);
			}
		}
		else   //Right branch
		{
			u = m->_parent->_parent->_leftChild;
			if (u->_color == RED)     //uncle is a red node
			{
				//Status III  
				m->_parent->_color = BLACK;
				m->_parent->_parent->_color = RED;
				u->_color = BLACK;
				m = m->_parent->_parent;
			}
			else      //The uncle node is black
			{
				if (m == m->_parent->_leftChild)  //Status II  
				{
					m = m->_parent;
					RotateR(t, m);
				}
				m->_parent->_color = BLACK;                  //Status one
				m->_parent->_parent->_color = RED;
				RotateL(t, m->_parent->_parent);
			}
		}
	}
	t->_color = BLACK;  //No matter how you adjust it, the root node must be black
}

I won't say much about finding the insertion position. I'll take a closer look. I'll mainly talk about adjusting the balance here:

Two cases of adjusting balance

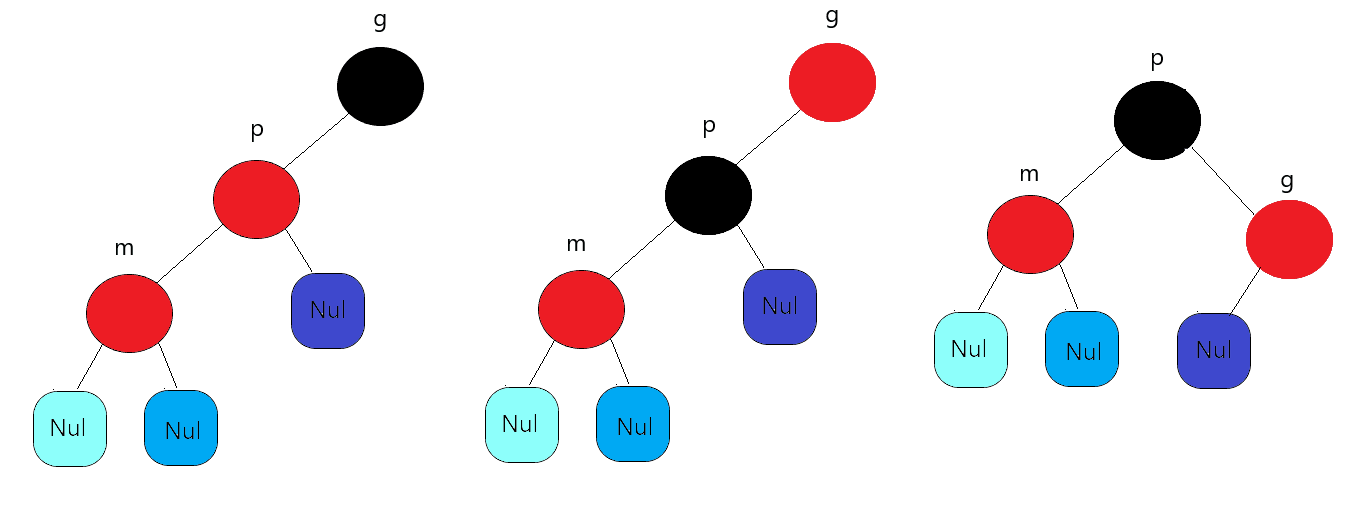
1, The uncle node is black

uncle may or may not exist. It doesn't matter. If it doesn't exist, it also points to the black empty node Nul set by ourselves

Case 1: the insertion node is inserted on the outside (single rotation)

We only need to change the parent node to black and the grandfather node to red first. We can achieve balance by single rotation

Case 2: the insertion node is inserted inside (double rotation)

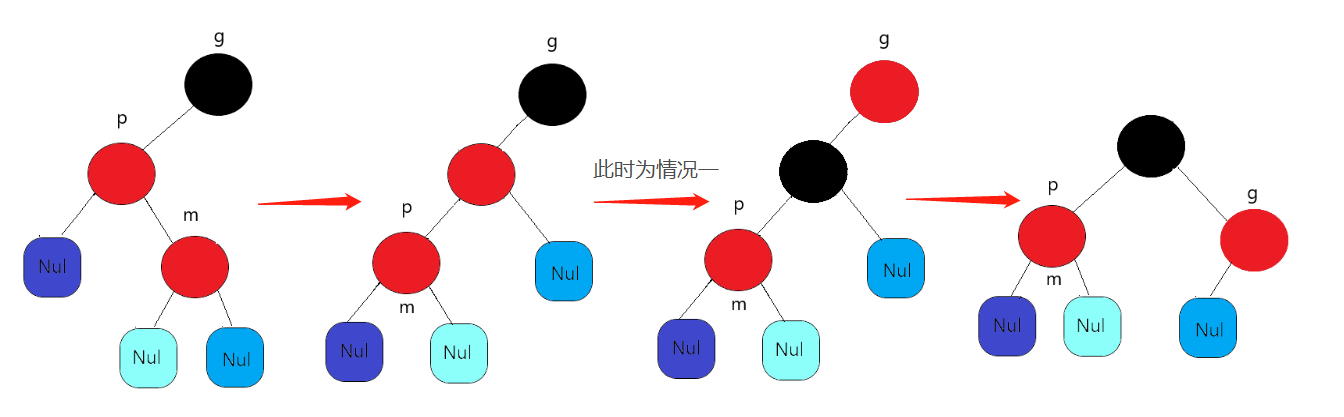
First, make it a single rotation to turn it into case one, and then color and rotate it through case one to achieve balance. Here is a small detail, that is, we need to catch m node to M's parent node in advance, because our goal is to make it a case one. Students who have carefully looked at the rotation function must have found that the parent node will rotate after rotation, Therefore, we need to trace the parent node according to the rotation function to make it become a case after rotation

2, The uncle node is red

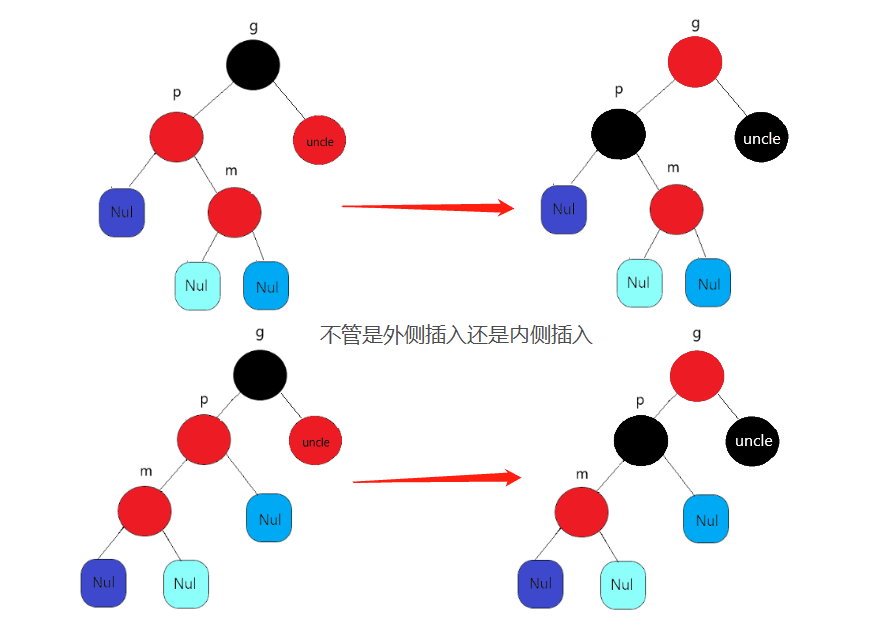
At this time, our processing is relatively simple. We only need to change the color of its father node and uncle node to black, the color of grandfather node to red, and then continue to adjust upward. At this time, it will be converted to case 1 or case 2 above, and then adjust according to the corresponding adjustment method

5, Deletion of red black tree

template<class Type>
void RBTree<Type>::_Remove(RBTreeNode<Type>*& t, const Type val)
{
	RBTreeNode<Type>* p = t;
	while (p != Nul)            //Find the node to be deleted
	{
		if (p->_Val == val)
			break;

		if (val > p->_Val)
			p = p->_rightChild;
		else
			p = p->_leftChild;
	}
	
	RBTreeNode<Type>* q;    

	if (p == Nul)   //The deleted node does not exist
		return;
	 
	if (p->_leftChild != Nul && p->_rightChild != Nul)   //The deleted node has left and right subtrees
	{
		q = p->_leftChild;

		while (q->_rightChild != Nul)
			q = q->_rightChild;

		p->_Val = q->_Val;
		p = q;
	}

	if (p->_leftChild != Nul)   //The deleted node has only one subtree
		q = p->_leftChild;
	else
		q = p->_rightChild;
	q->_parent = p->_parent;   //Hang the q node to the subtree of the parent node of the deleted node

	if (q->_parent == Nul) // The root node is deleted
	{
		t = q;
		t->_color = BLACK;
		delete p;
		return;
	}
	
	if (p == p->_parent->_leftChild)    //The parent node connects the child tree of p in the corresponding left tree or right tree
		p->_parent->_leftChild = q;
	else
		p->_parent->_rightChild = q;
	
	/*Adjust balance*/
	if (p->_color == BLACK)
	{
		if (q != Nul)   //Combination 4: directly exchange colors and delete the p node
			q->_color = BLACK;
		else            //Combination II
			Re_balance(t, q);
	}
	delete p;
}
template<class Type>
void RBTree<Type>::Re_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
	while (m != t)
	{
		RBTreeNode<Type>* b;
		if (m == m->_parent->_leftChild)     //Left branch
		{
			b = m->_parent->_rightChild;

			/*-—  Case 4 -——*/
			if (b->_color == RED)    
			{
				b->_color = BLACK;
				m->_parent->_color = RED;
				RotateL(t, m->_parent);
				b = m->_parent->_rightChild;
			}

			/*-—  Case 3 -——*/
			if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)  
			{
				b->_color = RED;
				if (m->_parent->_color == RED)
				{
					m->_parent->_color = BLACK;
					m = t;
				}
				else
					m = m->_parent;    //Go back up and continue to judge
			}
			else
			{
				/*-—  Case 2 -——*/
				if (b->_leftChild->_color == RED)  
				{
					b->_color = RED;
					b->_leftChild->_color = BLACK;
					RotateR(t, b);
					b = b->_parent;
				}
				/*-—  Case 1 -——*/
				b->_color = m->_parent->_color;
				m->_parent->_color = BLACK;
				b->_rightChild->_color = BLACK;
				RotateL(t, m->_parent);

				m = t;
			}
		}
		else   //Right branch
		{
			b = m->_parent->_leftChild;

			/*-—  Case 4 -——*/
			if (b->_color == RED)
			{
				b->_color = BLACK;
				m->_parent->_color = RED;
				RotateR(t, m->_parent);
				m = m->_parent;
			}

			/*-—  Case 3 -——*/
			if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)
			{
				b->_color = RED;
				if (m->_parent->_color = RED)
				{
					m->_parent->_color = BLACK;
					m = t;
				}
				else
					m = m->_parent;
			}
			else
			{
				/*-—  Case 2 -——*/
				if (b->_rightChild->_color == RED)
				{
					b->_color = RED;
					b->_rightChild->_color = BLACK;
					RotateL(t, b);
					b = b->_parent;
				}

				/*-—  Case 1 -——*/
				b->_color = m->_parent->_color;
				m->_parent->_color = BLACK;
				b->_leftChild->_color = BLACK;
				RotateR(t, m->_parent);

				m = t;
			}
		}
		t->_color = BLACK;
	}
}

How to find the deletion location and the processing of the child nodes of the deleted node are the same as that of the AVL tree. They are transformed into the situation that there is only one child tree or no child tree at most. Therefore, we won't talk about it here. We mainly talk about how to delete the nodes with different colors and positions during deletion.

Six situations encountered when deleting

Case 1:
If the deleted node is a RED node and a leaf node, you can delete it directly

Case 2:
The deleted node is RED node, and there is only one leaf node

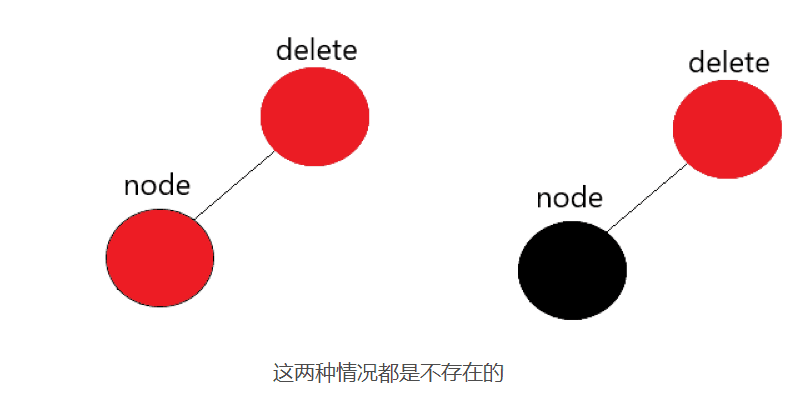
Explanation:
This situation does not exist, otherwise it will violate the nature of red black tree - the number of black nodes on each path is the same; Or it violates the nature of red black tree - red nodes cannot be connected

Case 3:
The deleted node is a BLACK node, and there is only one leaf node

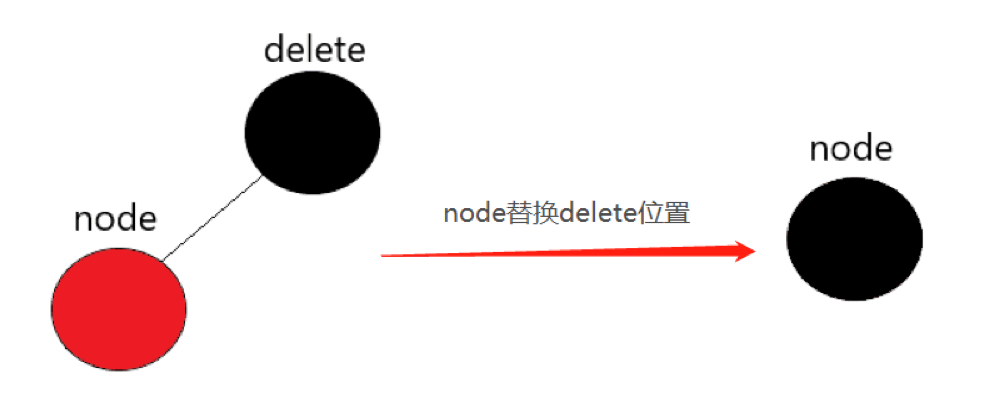
Explanation:
The leaf node color of this node can only be RED. If it is a BLACK node, it will still violate the nature of the RED BLACK tree - the number of BLACK nodes on each path is the same, so it can only be RED leaf nodes. Then directly change the leaf node color to BLACK and use the leaf node to replace the position of the deleted node to achieve balance

Situation IV and V
The deleted node has two nodes. Here, the deleted node may be RED or BLACK
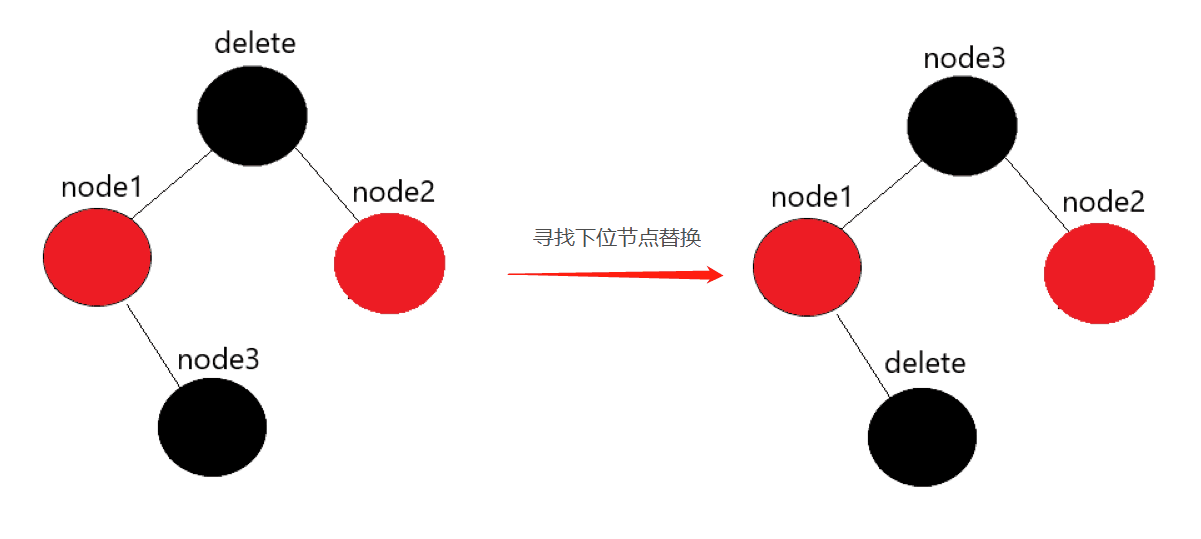Explanation:
The replacement search here is the same as the AVL tree. The node color here is not necessarily like this, but just an example. Therefore, after replacement, case 4 and 5 will be transformed into case 3 or case 6

Situation VI
The deleted node is a BLACK node and has no children.

In this case, there are four situations:

Case 1:
The brother node of the deleted node has a child node with the same direction

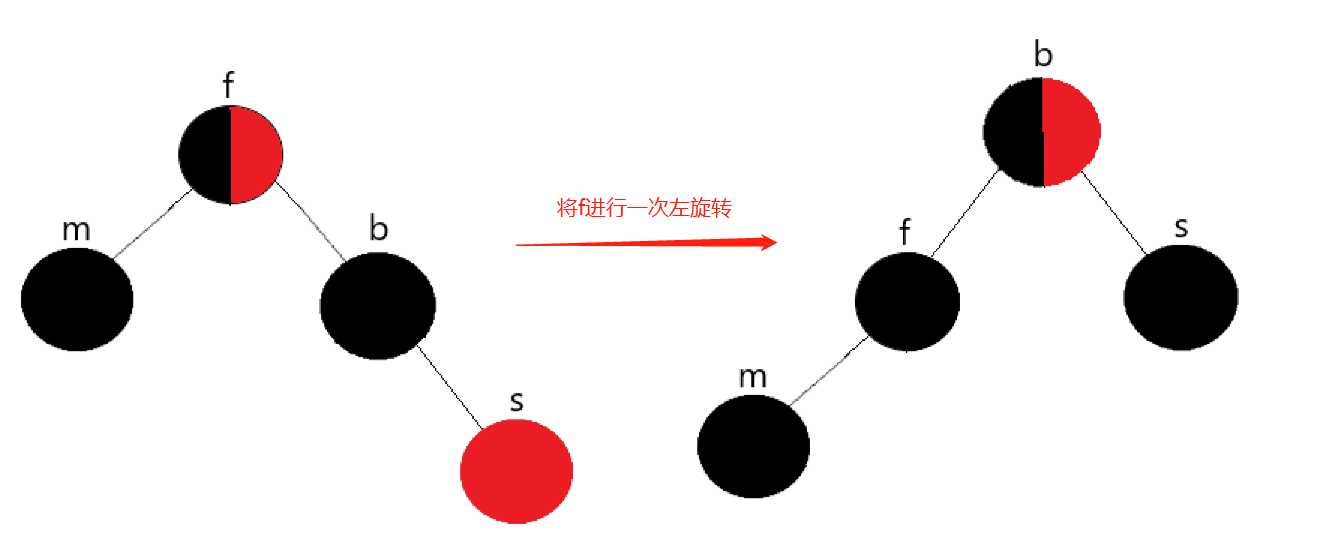
Explanation:
First swap the colors of the father node and the brother node, then rotate the father node to the left, and then delete the mine node to achieve balance.

Scenario 2:
The brother node of the deleted node has a child node in the opposite direction

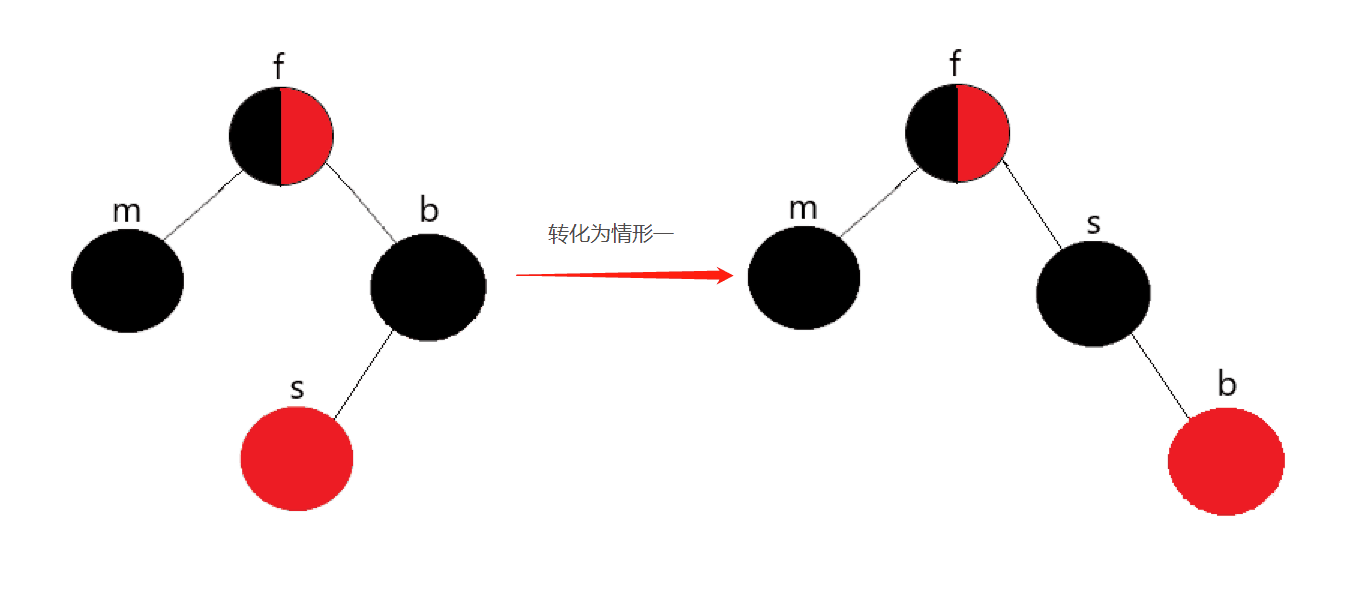
Explanation:
First, exchange the colors of the brother node and the son node, and then rotate the brother node to the right. At this time, it becomes case one. Then, conduct the operation of case one to achieve balance

Situation 3
The brother node has no red child nodes

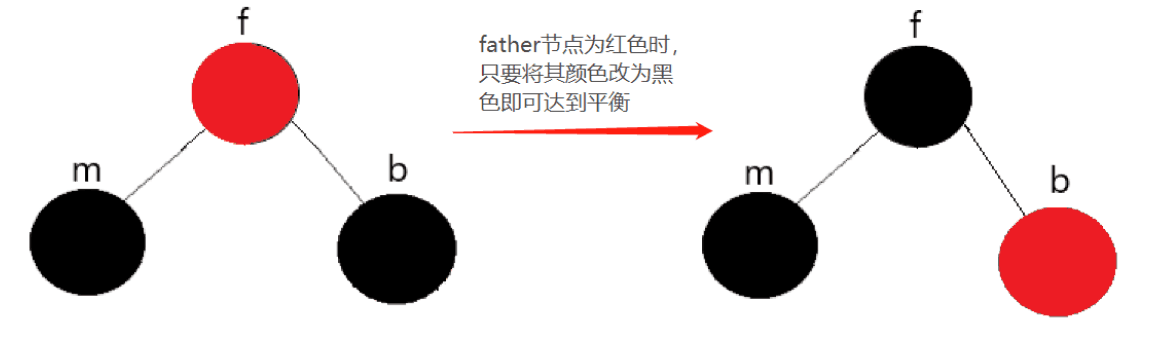
Explanation:
When the father node is red, first change the brother color to red, then change the father node color to black, and finally delete the mine node to achieve balance

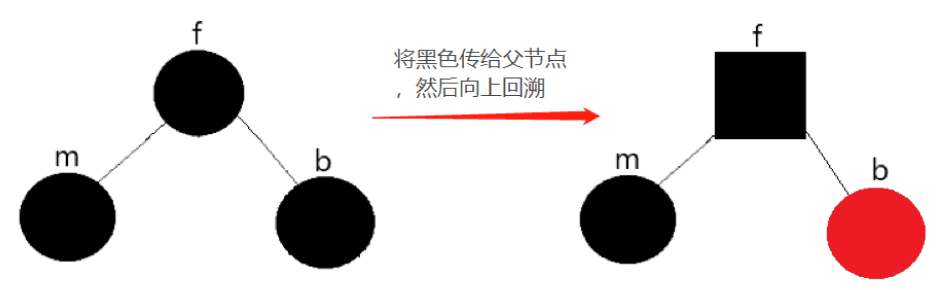
Explanation:
Here, careful friends can see that the father node has changed from round to black, which is called "double black". It is our assumed black. It is not real, but our own subjective imagination. The occurrence of this situation is that the mine node gives its own black to the father node, so we regard it as balanced, and its black is reduced, But the father is black, and now there is an extra weight, so it is double black. Of course, we need to delete this redundant black, so we need to change the color of the brother node to red, and then continue to backtrack up and continue to adjust the balance.

Situation 4
The brother node is red

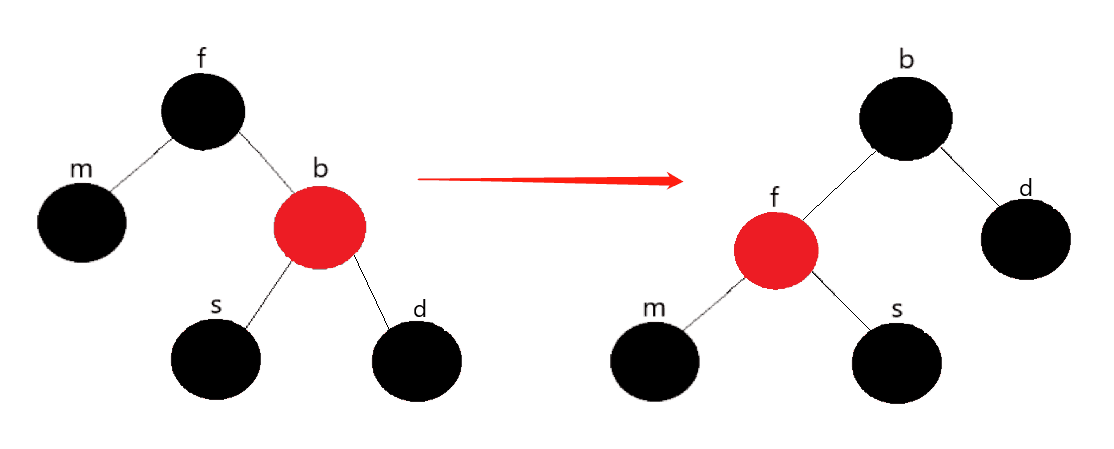
Explanation:
First adjust the color of the father and brother nodes, and then rotate the father node to the left. At this time, the new brother node is the son node, which is transformed into the case that the brother node is BLACK. In this way, it can be transformed into the other cases above for response adjustment.

6, Source code

#include<iostream>
#include<stack>
#include<vector>
using namespace std;
enum Color { BLACK = 0, RED = 1 };  //Set color

template<typename Type>    //Class, otherwise there may be an error when declaring a friend class due to the compiler version
class RBTree;

template<typename Type>
class RBTreeNode
{
	friend class RBTree<Type>;   //Become a friend class that can access private members of the node
public:
	RBTreeNode(Type val = Type())
		:_rightChild(nullptr), _leftChild(nullptr), _parent(nullptr), _Val(val), _color(RED)
	{}
	~RBTreeNode()
	{}
private:
	Type _Val;
	Color _color;
	RBTreeNode<Type>* _rightChild;
	RBTreeNode<Type>* _leftChild;
	RBTreeNode<Type>* _parent;
};

template<typename Type>
class RBTree
{
public:
	RBTree() :Nul(_BuyNode()), _root(Nul)
	{
		Nul->_leftChild = Nul->_rightChild = Nul->_parent = nullptr;
		Nul->_color = BLACK;
	}
public:
	void Insert(Type val = Type())
	{
		_Insert(_root, val);
	}
	void Remove(Type val = Type())
	{
		_Remove(_root, val);
	}
protected:
	void _Insert(RBTreeNode<Type>*& t,const Type val);
	void In_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m);
	void _Remove(RBTreeNode<Type>*& t, const Type val);
	void Re_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m);
	void RotateL(RBTreeNode<Type>*& t, RBTreeNode<Type>* p);
	void RotateR(RBTreeNode<Type>*& t, RBTreeNode<Type>* p);
protected:
	RBTreeNode<Type>* _BuyNode(const Type val = Type())
	{
		RBTreeNode<Type>* s = new RBTreeNode<Type>(val);
		s->_leftChild = s->_rightChild = Nul;
		return s;
	}
private:
	RBTreeNode<Type>* Nul;
	RBTreeNode<Type>* _root;
};

template<typename Type>
void RBTree<Type>::RotateL(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
	RBTreeNode<Type>* s = p->_rightChild;
	if (s->_leftChild != Nul)
		s->_leftChild->_parent = p;
	p->_rightChild = s->_leftChild;
	s->_parent = p->_parent;
	if (p->_parent == Nul)
		t = s;
	else if (p == p->_parent->_leftChild)
		p->_parent->_leftChild = s;
	else
		p->_parent->_rightChild = s;
	s->_leftChild = p;
	p->_parent = s;
}
template<typename Type>
void RBTree<Type>::RotateR(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
	RBTreeNode<Type>* s = p->_leftChild;
	if (s->_rightChild != Nul)
		s->_rightChild->_parent = p;
	p->_leftChild = s->_rightChild;
	s->_parent = p->_parent;
	if (p->_parent == Nul)
		t = s;
	else if (p == p->_parent->_leftChild)
		p->_parent->_leftChild = s;
	else
		p->_parent->_rightChild = s;
	s->_rightChild = p;
	p->_parent = s;
}
template<typename Type>
void RBTree<Type>::_Insert(RBTreeNode<Type>* &t, const Type val)
{
	RBTreeNode<Type>* p = t;
	RBTreeNode<Type>* pr = Nul;
	while (p != Nul)    //Find insertion location
	{
		if (val == p->_Val)  //The same data is not accepted
			return;

		pr = p;

		if (val > p->_Val)
			p = p->_rightChild;
		else
			p = p->_leftChild;
	}

	p = _BuyNode(val);
	if (pr == Nul)  // The first root node is inserted
	{
		t = p;
		t->_parent = pr;
	}

	if (val > pr->_Val)
		pr->_rightChild = p;
	else
		pr->_leftChild = p;
	p->_parent = pr;

	/*Adjust balance*/
	In_balance(t, p);
}
template<typename Type>
void RBTree<Type>::In_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
	while (m->_parent->_color == RED)
	{
		RBTreeNode<Type>* u;   //uncle node
		if (m->_parent == m->_parent->_parent->_leftChild)   //Left branch
		{
			u = m->_parent->_parent->_rightChild;
			if (u->_color == RED)     //Status 3: uncle s are red nodes
			{
				m->_parent->_color = BLACK;
				m->_parent->_parent->_color = RED;
				u->_color = BLACK;
				m = m->_parent->_parent;
			}
			else    //The uncle node is black
			{
				if (m == m->_parent->_rightChild)  //Status II  
				{
					m = m->_parent;
					RotateL(t, m);
				}
				m->_parent->_color = BLACK;                  //Status one
				m->_parent->_parent->_color = RED;
				RotateR(t, m->_parent->_parent);
			}
		}
		else   //Right branch
		{
			u = m->_parent->_parent->_leftChild;
			if (u->_color == RED)     //uncle is a red node
			{
				//Status III  
				m->_parent->_color = BLACK;
				m->_parent->_parent->_color = RED;
				u->_color = BLACK;
				m = m->_parent->_parent;
			}
			else      //The uncle node is black
			{
				if (m == m->_parent->_leftChild)  //Status II  
				{
					m = m->_parent;
					RotateR(t, m);
				}
				m->_parent->_color = BLACK;                  //Status one
				m->_parent->_parent->_color = RED;
				RotateL(t, m->_parent->_parent);
			}
		}
	}
	t->_color = BLACK;
}
template<class Type>
void RBTree<Type>::_Remove(RBTreeNode<Type>*& t, const Type val)
{
	RBTreeNode<Type>* p = t;
	while (p != Nul)
	{
		if (p->_Val == val)
			break;

		if (val > p->_Val)
			p = p->_rightChild;
		else
			p = p->_leftChild;
	}
	
	RBTreeNode<Type>* q;    

	if (p == Nul)   //The deleted node does not exist
		return;
	 
	if (p->_leftChild != Nul && p->_rightChild != Nul)   //The deleted node has left and right subtrees
	{
		q = p->_leftChild;

		while (q->_rightChild != Nul)
			q = q->_rightChild;

		p->_Val = q->_Val;
		p = q;
	}

	if (p->_leftChild != Nul)   //The deleted node has only one subtree
		q = p->_leftChild;
	else
		q = p->_rightChild;
	q->_parent = p->_parent;   //Hang the q node to the subtree of the parent node of the deleted node

	if (q->_parent == Nul) // The root node is deleted
	{
		t = q;
		t->_color = BLACK;
		delete p;
		return;
	}
	
	if (p == p->_parent->_leftChild)    //The parent node connects the child tree of p in the corresponding left tree or right tree
		p->_parent->_leftChild = q;
	else
		p->_parent->_rightChild = q;
	
	/*Adjust balance*/
	if (p->_color == BLACK)
	{
		if (q != Nul)   //Combination 4: directly exchange colors and delete the p node
			q->_color = BLACK;
		else            //Combination II
			Re_balance(t, q);
	}
	delete p;
}
template<class Type>
void RBTree<Type>::Re_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
	while (m != t)
	{
		RBTreeNode<Type>* b;
		if (m == m->_parent->_leftChild)     //Left branch
		{
			b = m->_parent->_rightChild;

			/*-—  Case 4 -——*/
			if (b->_color == RED)    
			{
				b->_color = BLACK;
				m->_parent->_color = RED;
				RotateL(t, m->_parent);
				b = m->_parent->_rightChild;
			}

			/*-—  Case 3 -——*/
			if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)  
			{
				b->_color = RED;
				if (m->_parent->_color == RED)
				{
					m->_parent->_color = BLACK;
					m = t;
				}
				else
					m = m->_parent;    //Go back up and continue to judge
			}
			else
			{
				/*-—  Case 2 -——*/
				if (b->_leftChild->_color == RED)  
				{
					b->_color = RED;
					b->_leftChild->_color = BLACK;
					RotateR(t, b);
					b = b->_parent;
				}
				/*-—  Case 1 -——*/
				b->_color = m->_parent->_color;
				m->_parent->_color = BLACK;
				b->_rightChild->_color = BLACK;
				RotateL(t, m->_parent);

				m = t;
			}
		}
		else   //Right branch
		{
			b = m->_parent->_leftChild;   //Sibling node

			/*-—  Case 4 -——*/
			if (b->_color == RED)
			{
				b->_color = BLACK;
				m->_parent->_color = RED;
				RotateR(t, m->_parent);
				m = m->_parent;
			}

			/*-—  Case 3 -——*/
			if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)
			{
				b->_color = RED;
				if (m->_parent->_color = RED)
				{
					m->_parent->_color = BLACK;
					m = t;
				}
				else
					m = m->_parent;
			}
			else
			{
				/*-—  Case 2 -——*/
				if (b->_rightChild->_color == RED)
				{
					b->_color = RED;
					b->_rightChild->_color = BLACK;
					RotateL(t, b);
					b = b->_parent;
				}

				/*-—  Case 1 -——*/
				b->_color = m->_parent->_color;
				m->_parent->_color = BLACK;
				b->_leftChild->_color = BLACK;
				RotateR(t, m->_parent);

				m = t;
			}
		}
		t->_color = BLACK;
	}
}
int main()
{
	RBTree<int> Rb;
	vector<int> iv = { 10, 7,  8, 15, 5, 6, 11, 13, 12 };
	for (int i = 0; i < iv.size(); ++i)
	{
		Rb.Insert(iv[i]);
	}

	Rb.Remove(11);
	Rb.Remove(13);
	Rb.Remove(8);
	Rb.Remove(12);
	Rb.Remove(6);

	return 0;
}