Under a more detailed classification, there are three common types of greedy questions
Greed is an idea that constantly selects the local optimal solution to achieve the global optimal solution. In other words, greed is constantly making the most favorable decisions for the present. It is unrealistic to classify all greedy problems in one breath according to the ubiquitous algorithm idea of greed.
Therefore, this paper focuses on three kinds of common greed (classified by the author according to his own understanding), "the highest cost performance", "the highest degree of overlap" and "the highest number of activities", and summarizes them, supplemented by relevant typical examples to help you get started with the greedy algorithm.
Best value for money
Relevant knowledge
we define cost performance as the amount obtained per unit of input / the amount invested per unit of input. In other words, high cost performance means
① high input of the same input / ② low input of the same input
generally, this kind of topic will give us many choices. We will sort the priority according to the cost performance. First choose the one with high cost performance, and then choose the one with secondary cost performance, until the one with the lowest cost performance. This is the simplest kind of greed in my opinion, which often involves only one ranking.
Related topics
Trade between mouse and cat - high gain with the same input

Reference ideas
in essence, it is to ask how the mouse can use the same input (cat food) to obtain the highest yield (spiced beans), so it is necessary to introduce a concept of cost performance. Obviously, the cost performance in this question can be defined only by the spiced beans available per unit of cat food. Then the general idea comes out. According to the cost performance of each room, sort the cost performance from high to low, and then exchange according to the high cost performance priority strategy.
Refer to AC code
#include<bits/stdc++.h>
using namespace std;
struct gat{
float amount,price,economy;
}gate[1005];
bool cmp(gat a,gat b){
return a.economy>b.economy;
} // Define the sort function's price / performance descending ranking conditions
int main(){
int num;
double money,gate_num,max_sum; // define money and gate number
ios::sync_with_stdio(false);
while(cin>>money>>gate_num){ // enter money and gate number
if(money==-1&&gate_num==-1)break;
for(int i=1;i<=gate_num;i++){ // iterate all the gates
cin>>gate[i].amount>>gate[i].price; // input the ith gate food amount and price
gate[i].economy=gate[i].amount/gate[i].price; // calculate the ith food economy
}
num=(int)gate_num; // Convert the floating-point number of the number of gates to integer form and save it in num
sort(gate+1,gate+num+1,cmp); // sort function performs price / performance descending order based on gate
max_sum=0; // Initialize maximum purchase
for(int i=1;i<=gate_num;i++){ // Adjust the purchase order according to the high cost performance priority strategy, that is, buy the high cost performance first and then the low cost performance
if(money-gate[i].price>=0){ //If you have enough money, buy it all;
max_sum+=gate[i].amount; //Update purchase volume
money-=gate[i].price; //Update the amount of money left
}
else{ //If the money is not enough, you can buy as much as you want
max_sum+=gate[i].amount*(money/gate[i].price); //Update purchase volume
money=0; //Update the amount of money left
}
}
printf("%.3f\n",max_sum); //Keep 3 decimal places
}
return 0;
}
Tianji horse racing - low input of the same amount


Reference ideas
students familiar with Tian Ji's horse racing know that the king's horse strategy is to first get the fastest horse, then divide the second fastest horse, and so on, and finally get the slowest horse, which is in descending order of horse speed, but our horse order can be drawn up randomly. Our goal is to get the most wins, so winning is the amount we pursue, and the type of horse consumed is our investment. In fact, there are many different strategies for defeating the same horse of the other party. We follow the principle of low input when obtaining the same amount. For the same horse of the other party, we try our best to send the one whose speed is the least higher than that of the other party, so as to ensure the increase of the same winning field, but consume the least horsepower. If you continue to follow this strategy, you can find the biggest win.
to achieve this idea, since the other party must launch the horse in descending order, we will also arrange our own horses in descending order, and then select the first horse that can defeat the other party in order, so as to realize the "horse makes the best use" mentioned above.
Refer to AC code
#include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
int x,y,w,n;
int tian[1000],wang[1000];
while(cin>>n){
if(n==0)break;
w=0,x=0,y=0;
for(int i=0;i<n;i++){
cin>>tian[i];
}
for(int i=0;i<n;i++){
cin>>wang[i];
}
sort(tian,tian+n,greater<int>()),sort(wang,wang+n,greater<int>());
while(x<n&&y<n){
if(tian[x]>wang[y])w++,x++,y++;
else y++;
}
cout<<(2*w-n)*200<<endl;
}
return 0;
}
Maximum overlap
Relevant knowledge
the topic context of this kind of topic can generally be translated into that several points move on a line. In the process of moving, there can be no intersection between points. Ask us how much time / time we should move at least. For example, when moving tables in the dormitory corridor, it is stipulated that only one table can be carried in a section of corridor, and then the tables are distributed in different bedrooms. Ask how to allocate reasonably to achieve the least number of handling.
in this kind of questions, we regard the whole movement of each individual as a line segment. In order to be more intuitive, we can draw at different altitudes, and then we can draw many line segments, as shown below:
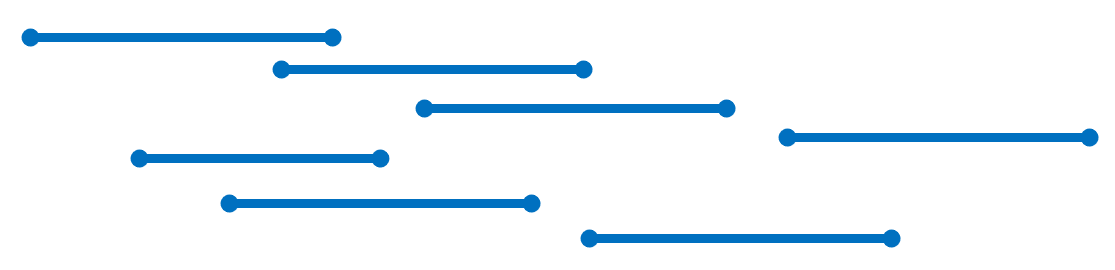
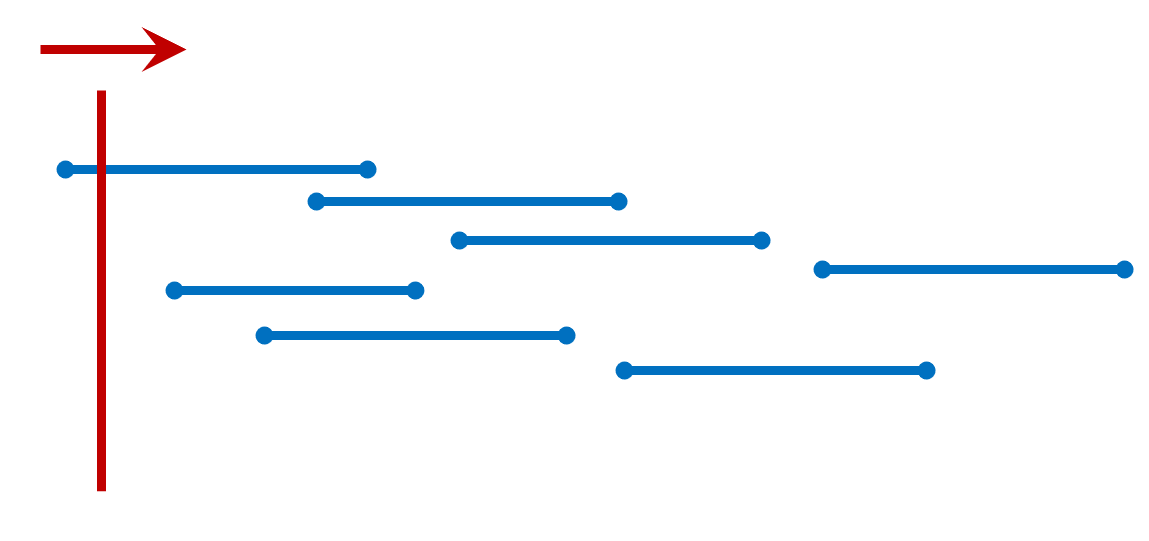
how many times to move at least is essentially a question. If a vertical line is moving to the right, how many horizontal lines can it intersect at most, as shown below:
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-I8q0BPxw-1646916048465)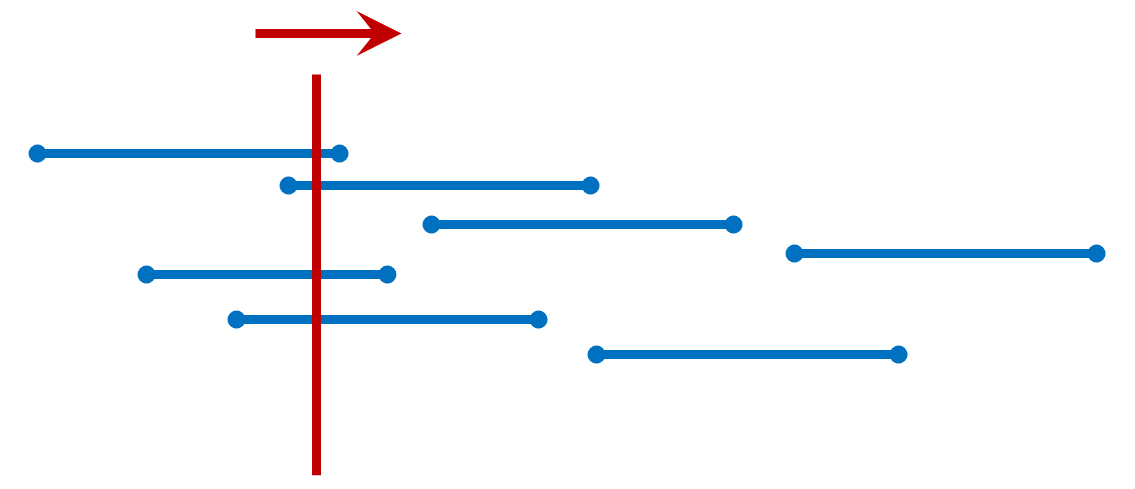
why can it be understood in this way? The number of intersections between the vertical line and the horizontal line actually reflects the number of things that can not be done at the same time. In other words, the minimum number of things to do separately.
how to find the maximum number of intersections? Obviously, according to our intuition, when we move to the place shown below, the number of intersections is the largest, and the number of intersections is 4:
[the external chain image transfer fails, and the source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-3mkj4vce-1646916048466) (C: \ users \ 49593 \ appdata \ roaming \ typora user images \ image-20220301230707895. PNG)]
but how to solve it in programming? We can use the loop to traverse the position occupied by each line segment, and the position occupied by the line segment is + 1. Therefore, for an abscissa x, how many line segments have appeared on this coordinate is its number. For further understanding, please look at the following topics.
Related topics
Move bedroom


Reference ideas
first deal with numbering problems 12, 34 and 56. In fact, they share the same place. Therefore, we need to make them equal, that is, add 1 to each endpoint and divide it by 2.
secondly, consider one direction. If the reverse transportation is essentially the same as the forward transportation, just change all the reverse transportation to the forward transportation.
finally, how to find the maximum overlap? Then add 1 (because it is a discrete point) to the point mark at each passing position. The maximum number of marks of the marked points is the maximum overlap. Multiply the maximum overlap by 10, then it is the minimum time required for the handling task.
Refer to AC code
#include<bits/stdc++.h>
using namespace std;
int main()
{
int i,j,T,N,s,t;
int r[200];
scanf("%d",&T);
while(T--)
{
scanf("%d",&N);
for(i=0;i<200;i++)
r[i]=0;
for(i=0;i<N;i++)
{
scanf("%d%d",&s,&t);
if(s>t){
j=s;s=t;t=j;
}
for(j=(s-1)/2;j<=(t-1)/2;j++)
r[j]++;
}
t=r[0];
for(i=1;i<200;i++)
if(t<r[i]) t=r[i];
printf("%d\n",t*10);
}
return 0;
}
Maximum number of activities
Relevant knowledge
such questions will tell us that there are many activities, each of which occupies a certain period of time, and then ask you to find the maximum number of activities that can be arranged.
the solution of this type of question is to sort the activities in ascending order according to the end time of the activities, select the earliest completed ones, and then select the next early completed ones on the premise that they do not conflict with the former until they are not met. The total number selected is the maximum number of activities required. (it can be proved by the method of counter evidence, which can be directly recorded as the conclusion)
Related topics
This summer vacation is not AC
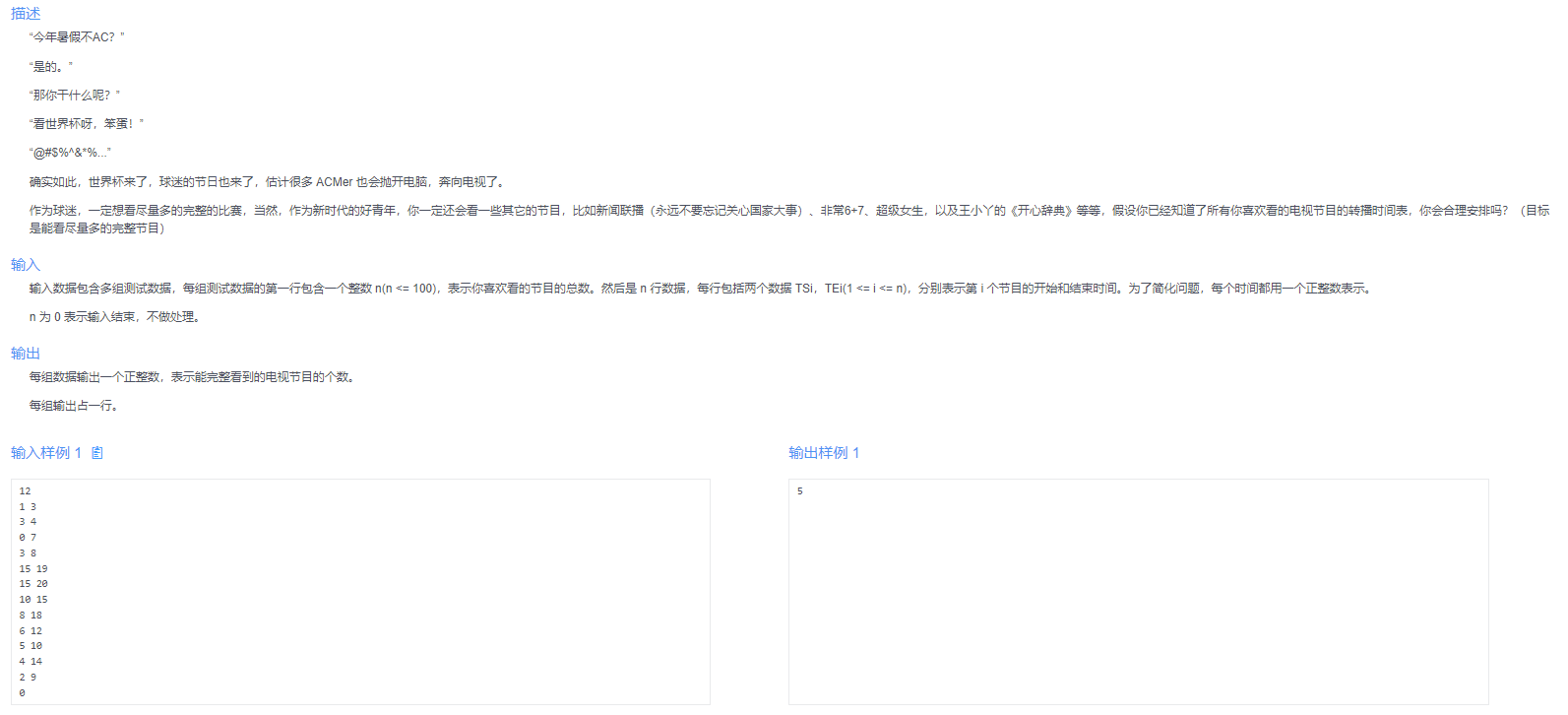
Reference ideas
since there are multiple programs, we open an array of programs. Since each program has two attributes of start time and end time, we use the structure to store the program information, so we use the structure array to store the information of these programs. Sort in ascending order according to the end time, select the earliest completed, and then select the second early completed on the premise that it does not conflict with the former. Know the unsatisfied position, and the total number selected is the maximum number of activities required.
it should be noted that since there are multiple groups of test data, data initialization must be carried out in each round of summary.
Refer to AC code
#include<bits/stdc++.h>
using namespace std;
struct jiemu{ //Define a structure to store the start time and two data of the program
int a;
int b;
};
bool cmp(jiemu x, jiemu y){ //When sorting, sort from small to large according to the end time. If the end time is the same, sort from small to large according to the start time
if(x.b==y.b) return x.a>y.a;
return x.b<y.b;
}
int main()
{
int x,y,s,N;
jiemu jm[100];
ios::sync_with_stdio(false);
while(cin>>N){
if(N==0) break;
x=0,y=1,s=1; //In the case of a loop, each initialization is very important. The initialization content is everything related to the result
for(int i=0;i<N;i++){
cin>>jm[i].a>>jm[i].b;
}
sort(jm,jm+N,cmp);
while(x<N&&y<N){ //The logic here must be consistent with, otherwise it will make mistakes
if(jm[x].b<=jm[y].a) s++,x=y,y++; //Find the appropriate length plus one, update the latest program x to the previous y, and then move y to the right
else y++; //Not found, y or right
}
cout<<s<<endl;
}
return 0;
}