The sequential array searches for a value

The basic idea of binary search is that the search interval must be orderly
In this paper, all search is based on the closed interval. At this time, the condition in while should be written as l < = R
If you search by the open interval (r=nums.size()), the condition in while should be written as l < R
A return value of - 1 indicates that the target was not found

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]==target) return mid;
            else if(nums[mid]<target) l=mid+1;
            else r=mid-1;
        }
        return -1;
    }
};

Search insertion location

Title Link

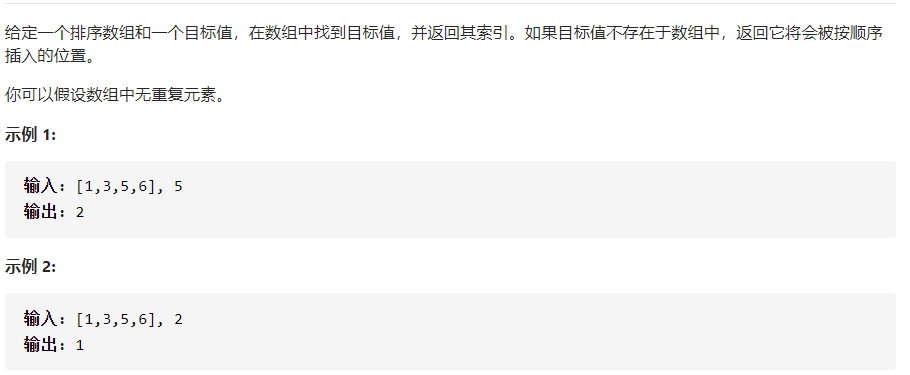
Based on the search, this question requires that if the searched element does not exist, it should return to the position where it should be inserted

We just need to change the return value of the above program to the left interval l
Analysis: when the program finds the target, it will return from return mid
When the target is not found, it will break the while condition and return
There are two situations to break the while condition: l > r because l=mid+1 or l > r because r=mid-1 (because l and R must be together in the last step of the search)
Because l=mid+1 indicates that the target is larger than mid and should be inserted after the current one, so l=mid+1,
The other case is the same, so l should be returned in both target cases

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]==target) return mid;
            else if(nums[mid]<target) l=mid+1;
            else r=mid-1;
        }
        return l;
    }
};

Sort the array to find the first and last positions of elements

Title Link

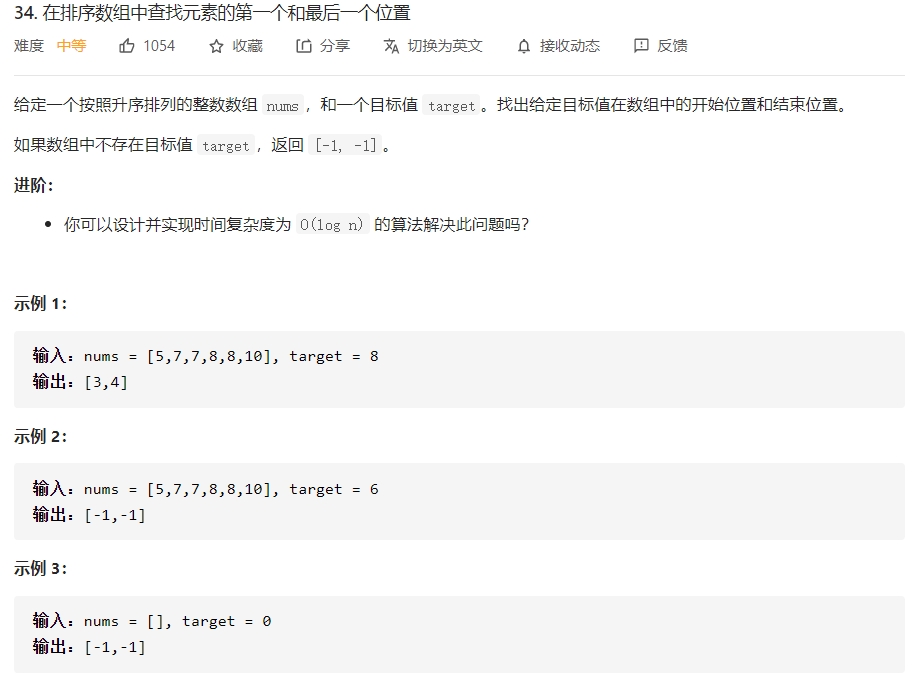
This question is different from the previous question. There may be several target elements
When mid finds the target, it is not necessarily the first or last target element,
For example, 1,2,3,3,3,4,5
Therefore, for finding the left boundary, we should let the search interval search the left half of the array, that is, r=mid-1
The right boundary is searched in the right half, i.e. l=mid+1
Note that the judgment condition should be added=

class Solution {
    int lowerBound(vector<int>& nums, int target,int l,int r){
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]>=target) r=mid-1;
            else l=mid+1;
        }
        return l;
    }
    int upperBound(vector<int>& nums, int target,int l,int r){
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]<=target) l=mid+1;
            else r=mid-1;
        }
        return r;
    }
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int low=lowerBound(nums,target,0,nums.size()-1);
        int up=upperBound(nums,target,0,nums.size()-1);
        if(low>up) return {-1,-1};
        return {low,up};
    }
};

Find the first index larger than the target element

Find elements larger than the goal, then the goal of this problem is not the goal of the real solution (it's messy)
That is, the search logic should be in num [mid] > target
There are two elements required to find the title, current num [mid] > target & & num [mid-1] < = target
Or mid == left. This condition means that the current is the last step of the search. At this time, l and r must be together
The pre judgment condition is num [mid] > target, indicating that the current l/r/mid must be the first position greater than the target
Return l is to facilitate understanding and memory

int lowBoundnum(int[] nums,int target,int left, int right) {
        while (left <= right) {
            //Find the intermediate value
            int mid = left + ((right - left) >> 1);
            //Greater than the target value
            if (nums[mid] > target) {
                 //Return mid
                if (mid == left || nums[mid-1] <= target) {
                    return mid;
                }
                else{
                    right = mid -1;
                }

            } else if (nums[mid] <= target){
                left = mid + 1;
            }
        }
        //All elements are smaller than the target element
        return -1;
    }

Find the last index smaller than the target element

Similarly

int upperBoundnum(int[] nums,int target,int left, int right) {

        while (left <= right) {

            int mid = left + ((right - left) >> 1);
             //Less than target value
            if (nums[mid] < target) {
            //Check whether it is the last digit in the current interval. If the current is less than and the next digit is greater than, return the current value
                if (mid == right || nums[mid+1] >= target) {
                    return mid;
                }
                else{
                    left = mid + 1;
                }

            } else if (nums[mid] >= target){
                right = mid - 1;
            }
        }
        //No information found
        return -1;
    }

Search rotated sorted array

Title Link

The array in this question is an ordered non repeating array obtained by rotation, so it can be regarded as two ordered arrays spliced together
So for mid, we should first judge which ordered array it is in
Note that the minimum value nums[l] of the preceding array must be greater than the maximum value nums[r] of the following array
Therefore, if num [mid] > = num [l], then mid is the array in front
Num [mid] > target & & target > = num [l] judge whether the target is in the front array. If not, the target may be in the front array or in the back array

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]==target) return mid;
            if(nums[mid]>=nums[l]){
                if(nums[mid]>target&&target>=nums[l]) r=mid-1;
                else l=mid+1;  
            }
            else{
                if(nums[mid]<target&&target<=nums[r]) l=mid+1;
                else r=mid-1;
            }
        }
        return -1;
    }
};

Search for a rotated array with duplicate sort

Title Link

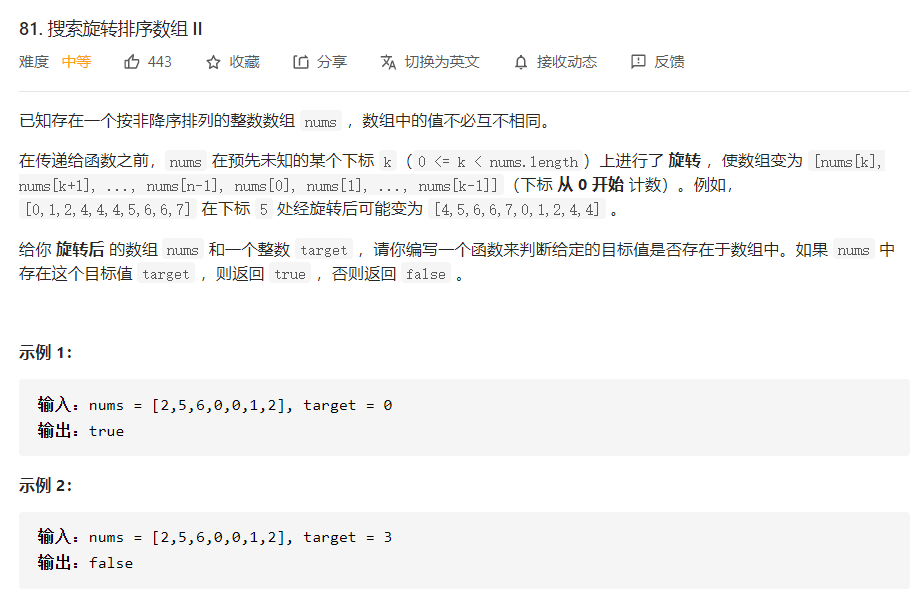
This problem has repeated rotation array. When 1,3,1,1,1 occurs, the previous program will not work
At this point, if (Num [mid] = = num [l]) {L + +; continue;} Move the left boundary by one bit, recalculate the mid, and remove the duplication in disguise.

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[mid]==target) return true;
            if(nums[mid]==nums[l]){
                l++;
                continue;
            }
            if(nums[mid]>nums[l]){
                if(nums[mid]>target&&target>=nums[l]) r=mid-1;
                else l=mid+1;
            }
            else{
                if(nums[mid]<target&&target<=nums[r]) l=mid+1;
                else r=mid-1;
            }
        }
        return false;
    }
};

Find minimum value of rotation array

Title Link

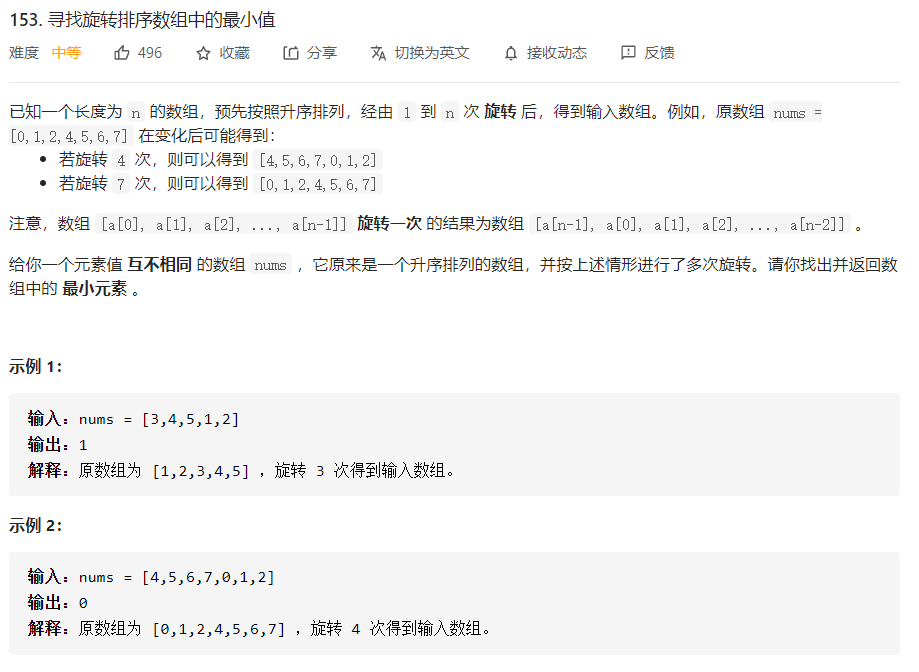
In different cases, if the search interval enters the monotone interval, Num [l] must be the smallest
If not, judge whether mid is in the front array or the back array as before
If mid is in the front array, the minimum value must be in the back
If mid is in the following array, the minimum value must be within this interval
Note that r=mid instead of r=mid-1, because the position of R may be the minimum

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=l+((r-l)>>1);
            if(nums[l]<=nums[r]) return nums[l];
            if(nums[l]<=nums[mid]){
                l=mid+1;
            }
            else if(nums[l]>nums[mid]){
                r=mid;
            }
        }
        return -1;
    }
};