We introduced the binary search tree and two higher-level data structures, set and mapping, which are implemented by the binary search tree.
Tree data structure plays an important role in the field of computer. It is important because trees can produce many extensions, change or restrict the nature of tree data structure slightly in the face of different problems, thus producing different data structures and solving different problems efficiently.
In the following four chapters, we will show you four examples of different trees: stack line segment tree dictionary tree and collect it. Through the study of these different trees, I hope you can appreciate the flexibility of the data structure, and think about the design of the data structure. Learn four different tree structures, but also have a deeper understanding of data structures.
Priority queue
What is the priority queue?
Ordinary queue: FIFO; FIFO
Priority queue: No relationship between the order of arrival and the order of arrival; early arrival and priority are related to those with higher priority (hospital, patient priority)
Task scheduling in the operating system, dynamically select the highest priority tasks to execute. If our task is not dynamic, then we only need a sort algorithm.
While dealing with old tasks, new tasks will be added constantly, so the keywords here (dynamic)
We can't determine how many tasks we have at the beginning, but we have to use the priority queue dynamically because there are always new elements and old elements in the queue.
AI in the game (soldier in LOL)

When facing several enemies at the same time, use the priority queue and fight with the highest priority (the closest distance, the most disabled blood? ) New enemies are approaching and moving.
Interfaces for priority queues (essentially still a queue)
Interface Queue<E> void enqueue(E) E dequeue() E getFront() int getSize() boolean isEmpty()
For our priority queue, when implementing these interfaces, the specific functions implemented by these interfaces will be different. The biggest difference lies in who is the first element of the team and who are the two operations. At this time, the outgoing element should be the element with the highest priority, and the element of the head of the team should also be the element with the highest priority, not the one that entered first.
Different underlying implementations can be used:
Ordinary linear structure: There is an operation "queue" is O(n) level, for n elements, its time complexity is n^2 level, relatively speaking, it is a very slow. Whether previously linked list implementations were used in set mapping or dynamic arrays were used in queues, O(n) operations were slow.
Sequential Linear Structure: Maintaining order requires O(n) to be on the team and O(1) to be on the team.

They have one disadvantage: they can be implemented by themselves using dynamic arrays or linked lists as exercises to compare with heaps.
The entry and exit operations of the heap can be O(logn) level.
And unlike the binary search tree in front of us, it's not the average O(logn), but the worst O(logn), which makes the heap fairly efficient.
Basic Representation of Reactors
Heap is the bottom implementation of priority queue. In computer science, we usually see that O(logn) is related to trees, not necessarily an explicit tree construction; for example, merge and sort in sorting, fast sort is nlogn level, and tree is not used in sorting process, but the recursive process actually forms a recursive tree.
The heap itself is a tree, the Binary Heap.
Binary heap is a complete binary tree.
- Full Binary Tree Concept: Except for leaf nodes, the left and right children of all nodes are not empty, that is, a full Binary Tree, as shown below.
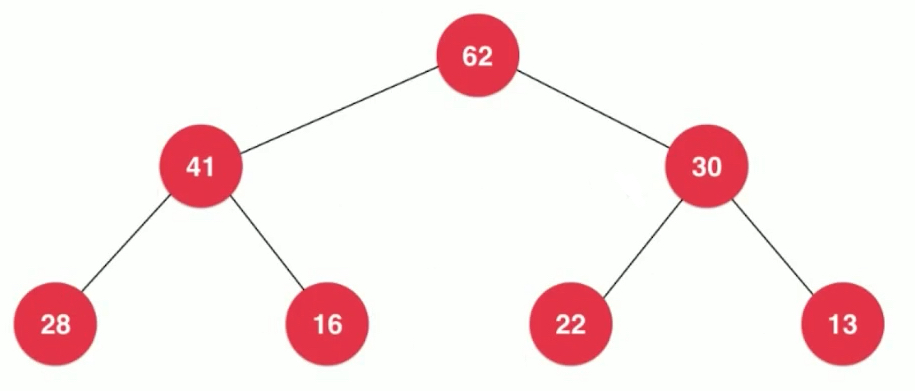
All nodes have left children and right children, which is a full binary tree.
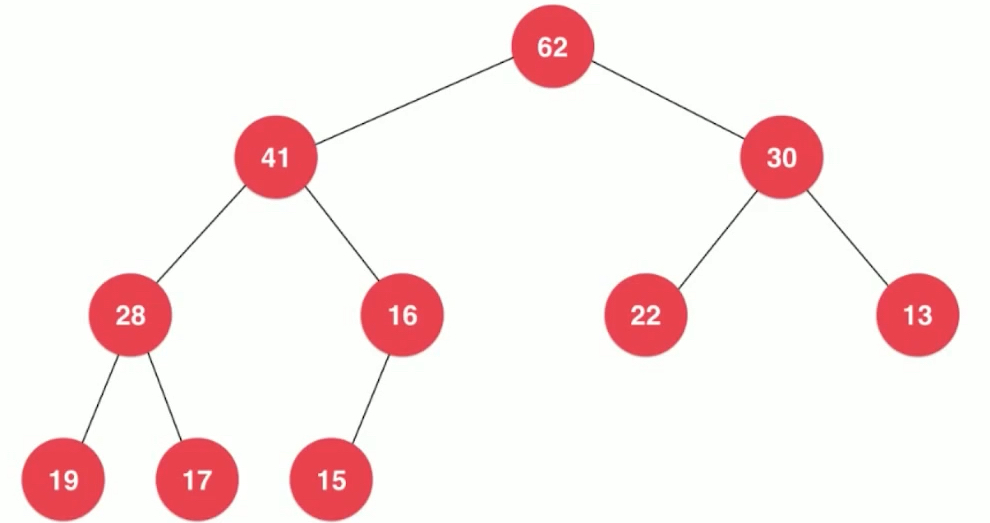
As shown above, it is a complete binary tree. It is not necessarily a full binary tree, but the part it dissatisfied with must be on the lower right. How many layers in a full binary tree correspond to how many nodes become a fixed thing. The nodes we want to join do not correspond to a whole layer, so the top layer is full, and the next layer is arranged from left to right.
The bottom layer must be leaf nodes, and the upper layer, even if there are leaf nodes, must be distributed on the right side. Complete Binary Tree: The shape of a tree by layering elements in order
Properties of Binary Reactor
The value of a node in the heap is always less than the value of its parent node. (The values of all nodes are greater than or equal to the values of their child nodes)
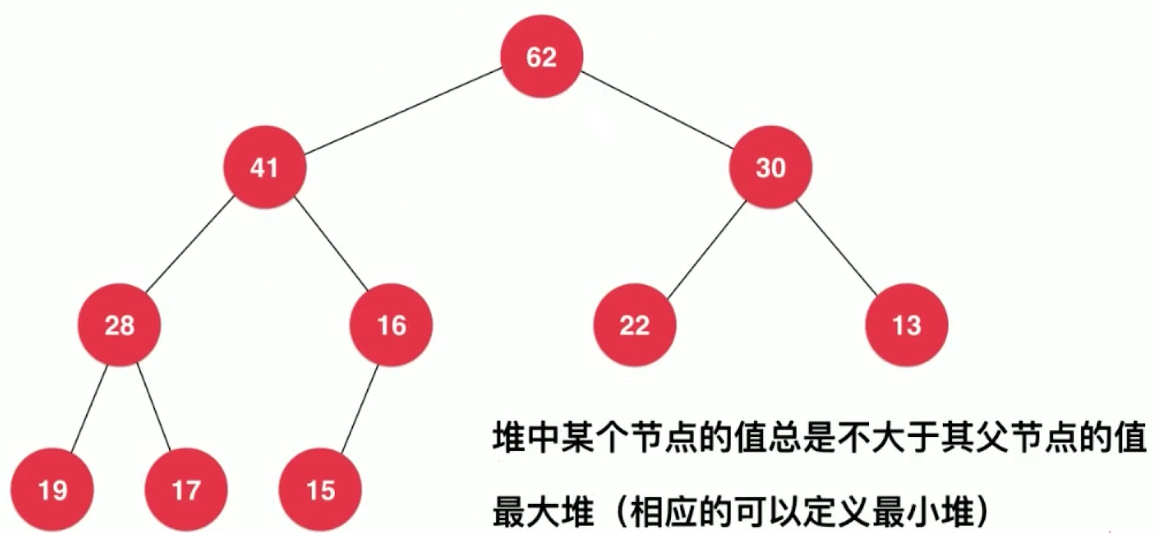
In this way, we get the largest heap, and we can also define the smallest heap accordingly. To some extent, the largest heap and the smallest heap can be unified, because what is big and what is small is what we can define.
It only guarantees that its father node is bigger than itself, but there is no necessary connection between the node's hierarchy and the node's size. For example, the number of layers in the second layer is smaller than that of any element in the third layer, but the value is not less than that.
Because of the complete binary tree, put it in sequence.
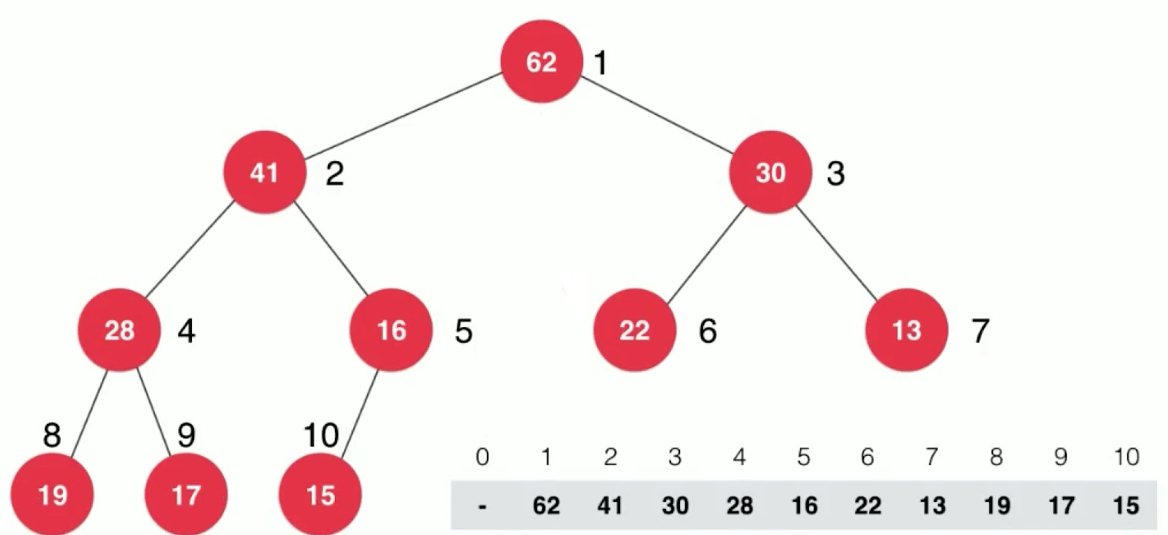
We can use such an array to represent the complete binary tree. Array storage node i's left and right children's rules.
parent(i) = i/2 left child(i) = 2*i; right child(i) = 2*i+1;
Mathematical induction can be used to prove that the above relationship is valid for a complete binary tree. The general array storage binary heap starts with 1, and the formula is as follows. If you start at 0, there will be an offset.
parent(i) = (i-1)/2 left child(i) = 2*i+1; right child(i) = 2*i+2;
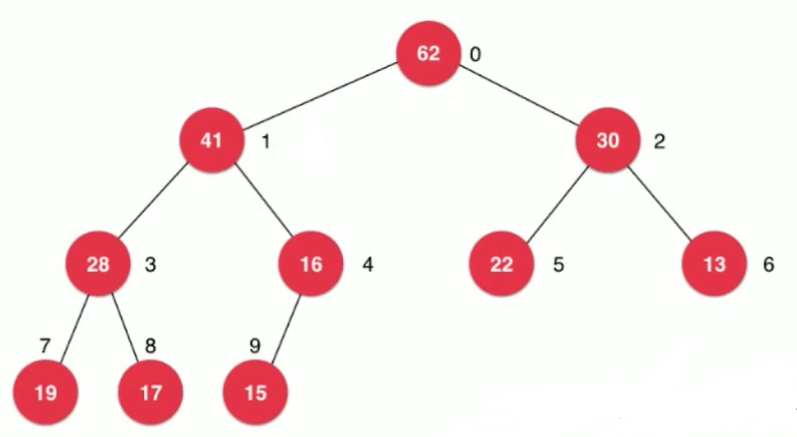
The formula can be verified by the graph.
Complete the basic implementation of the heap
package cn.mtianyan.heap; import cn.mtianyan.array.Array; public class MaxHeap<E extends Comparable<E>> { private Array<E> data; /** * Parametric constructor, incoming capacity, calling array construction with capacity * * @param capacity */ public MaxHeap(int capacity) { data = new Array<>(capacity); } /** * Default parametric constructor */ public MaxHeap() { data = new Array<>(); } /** * Returns the number of elements in the heap * * @return */ public int size() { return data.getSize(); } /** * Is the return heap empty? * * @return */ public boolean isEmpty() { return data.isEmpty(); } /** * Calculate the index value of the parent node of the incoming index * * @param index * @return */ private int parent(int index) { if (index == 0) throw new IllegalArgumentException("index 0 doesn't have parent."); return (index - 1) / 2; } /** * Calculate the index value of the left child of the incoming index * * @param index * @return */ private int left(int index) { return (2 * index + 1); } /** * Calculate the index value of the right child node of the incoming index * * @param index * @return */ private int right(int index) { return (2 * index + 2); } }
Adding elements and IFT Up to the heap
Adding elements from the user's point of view involves a very common operation in the heap, Sift Up, from the point of view of heap internal implementation.
A process of floating elements in a heap.
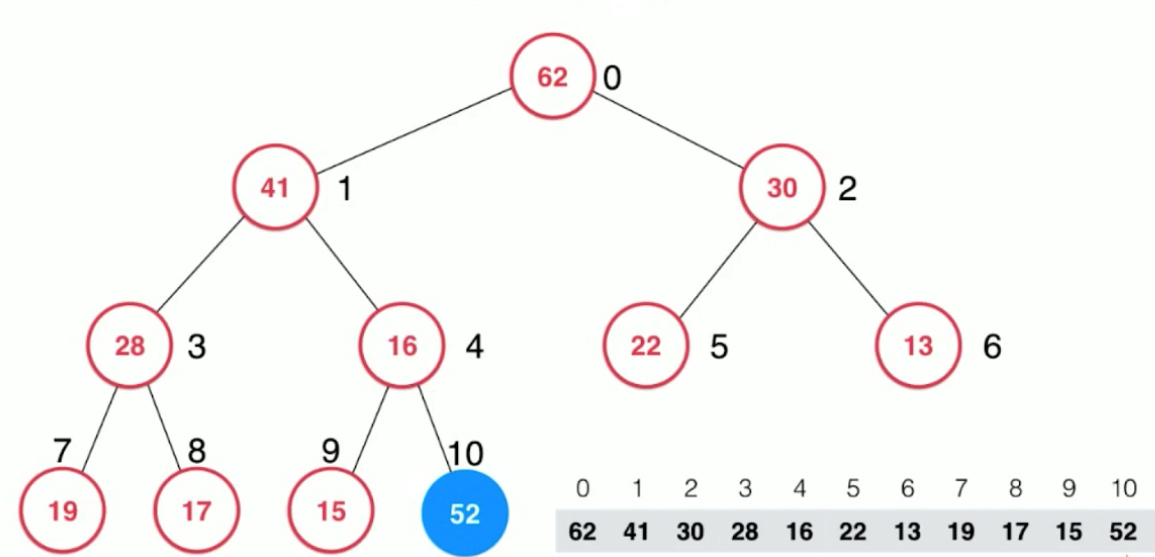
Adding elements is very simple, just add them directly to the array, but you can see that the tree structure at this time does not meet the requirements of the largest heap: the father is the largest, and the son of 16 is larger than 16. So 52 has to perform the float operation. How can a good pile go wrong? The only reason is that 52 nodes will only be added, so it only needs to compare 52 with its father node constantly. If the father is small, he will exchange with his father, and float up until 52 is no bigger than his father.
Here, 52 and 16 and 41 are interchanged twice.
Coding adds elements to the heap
/** * Exchange the element values of the two positions of the incoming index * * @param i * @param j */ public void swap(int i, int j) { if (i < 0 || i >= size || j < 0 || j >= size) throw new IllegalArgumentException("Index is illegal."); E temp = data[i]; data[i] = data[j]; data[j] = temp; }
Adding a method to swap the positions of two elements in an array.
/** * Adding element methods to the heap. * * @param e */ public void add(E e) { data.addLast(e); siftUp(data.getSize() - 1); } /** * index The element floats up for position i. * * @param i */ private void siftUp(int i) { // When the floating element is larger than the father, continue to float. And it can't float above zero. // Until i equals zero or is smaller than the father node. while (i > 0 && data.get(i).compareTo(data.get(parent(i))) > 0) { // Adding method swap to array Array data.swap(i, parent(i)); i = parent(i); // This sentence brings i to a new location, so that the loop can see if the new location is larger. } }
Remove the largest element in the heap and IFT Down
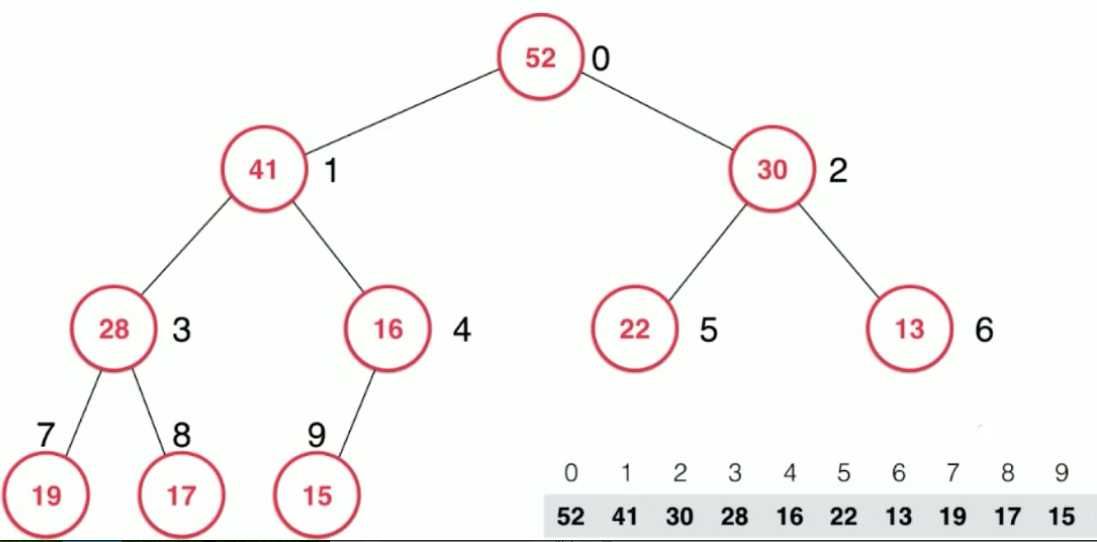
The maximum heap can only take the largest element, the position of the array is 0, after it is taken out. The operation of merging the two subtrees is troublesome.
We can fill the top of the heap with the last element and sink it constantly. Each time, compare with the two children and choose the largest element of the two children. If the largest element of the two children is bigger than itself, then it will exchange position with the largest one of the two children. The new position of 16 may still sink, again compared with the children.
Programming implementation
/** * The largest element in the heap * * @return */ public E findMax() { if (data.getSize() == 0) throw new IllegalArgumentException("Can not findMax when heap is empty."); return data.get(0); } /** * Remove the largest element from the heap * * @return */ public E extractMax() { E ret = findMax(); data.swap(0, data.getSize() - 1); // The 0 position element is interchanged with the last element. data.removeLast(); // Delete the last element at this point (maximum) siftDown(0); // siftDown for 0 return ret; } /** * k Location element downward * * @param k */ private void siftDown(int k) { // The k node is already a leaf node and no child is needed to sink. k's left child index = size has crossed the line, and it must be worthless. while (left(k) < data.getSize()) { int j = left(k); // In this cycle, data[k] and data[j] exchange locations // The right child may not exist, if there is a right child, the value of the right child is greater than that of the left child. if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) j++; // At this point, j is stored in the index of the right child because of ++. // data[j] is the maximum in leftChild and rightChild if (data.get(k).compareTo(data.get(j)) >= 0) break; // No violation of the nature of the heap when it is larger than the end. data.swap(k, j); k = j; } }
package cn.mtianyan; import cn.mtianyan.heap.MaxHeap; import java.util.Random; public class Main { public static void main(String[] args) { int n = 1000000; MaxHeap<Integer> maxHeap = new MaxHeap<>(); Random random = new Random(); for(int i = 0 ; i < n ; i ++) maxHeap.add(random.nextInt(Integer.MAX_VALUE)); int[] arr = new int[n]; for(int i = 0 ; i < n ; i ++) arr[i] = maxHeap.extractMax(); for(int i = 1 ; i < n ; i ++) if(arr[i-1] < arr[i]) throw new IllegalArgumentException("Error"); System.out.println("Test MaxHeap completed."); } }
Operation results:
Here's heap sorting. Sorting a million numbers is fast. Real heap sorting has optimization space. Now it is time to throw data in and take it out one by one. But using the idea of heap organization data, in-situ sorting can be achieved.
The time complexity of add and extractMax is O(logn) or O(h) of the binary tree, but because the heap is a complete binary tree, it will never degenerate into a linked list.
Heapify and replace operations
replace: After removing the largest element, put in a new element
Implementation: Max can be extracted first, then add ed, twice O(logn) operations
Implementation: You can directly replace the top element with a later Sift Down, an O(logn) operation
/** * Take out the largest element in the heap and replace it with element e * @param e * @return */ public E replace(E e){ E ret = findMax(); data.set(0, e); siftDown(0); return ret; }
heapify: Arbitrary arrays arranged into piles of shapes
/** * Arbitrary arrays are organized into piles of shapes * * @param arr */ public MaxHeap(E[] arr) { data = new Array<>(arr); for (int i = parent(arr.length - 1); i >= 0; i--) siftDown(i); }
Heapify is a siftdown operation that starts upside down from the father node of the last element.
Heapify's Algorithmic Complexity
The algorithm complexity is O(nlogn) by inserting n elements into an empty heap one by one.
heapify process, the algorithm complexity is O(n)
package cn.mtianyan.heap; import java.util.Random; public class CompareHeapifyHeap { private static double testHeap(Integer[] testData, boolean isHeapify){ long startTime = System.nanoTime(); MaxHeap<Integer> maxHeap; if(isHeapify) maxHeap = new MaxHeap<>(testData); else{ maxHeap = new MaxHeap<>(); for(int num: testData) maxHeap.add(num); } int[] arr = new int[testData.length]; for(int i = 0 ; i < testData.length ; i ++) arr[i] = maxHeap.extractMax(); for(int i = 1 ; i < testData.length ; i ++) if(arr[i-1] < arr[i]) throw new IllegalArgumentException("Error"); System.out.println("Test MaxHeap completed."); long endTime = System.nanoTime(); return (endTime - startTime) / 1e9; } public static void main(String[] args) { int n = 10000000; Random random = new Random(); Integer[] testData = new Integer[n]; for(int i = 0 ; i < n ; i ++) testData[i] = random.nextInt(Integer.MAX_VALUE); double time1 = testHeap(testData, false); System.out.println("Without heapify: " + time1 + " s"); double time2 = testHeap(testData, true); System.out.println("With heapify: " + time2 + " s"); } }
Data at the level of 1 million
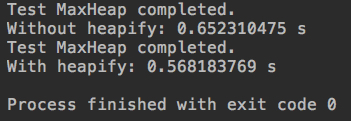
10 million-level data
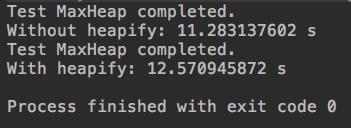
It can be seen that heapify operates faster at 1 million, but it is faster at 10 million without heap.
Heap-based priority queue
package cn.mtianyan.queue; import cn.mtianyan.heap.MaxHeap; public class PriorityQueue<E extends Comparable<E>> implements Queue<E> { private MaxHeap<E> maxHeap; public PriorityQueue(){ maxHeap = new MaxHeap<>(); } @Override public int getSize(){ return maxHeap.size(); } @Override public boolean isEmpty(){ return maxHeap.isEmpty(); } @Override public E getFront(){ return maxHeap.findMax(); } @Override public void enqueue(E e){ maxHeap.add(e); } @Override public E dequeue(){ return maxHeap.extractMax(); } }
Priority queues can use dynamic arrays or linked lists, or maintain a sequential linear structure (dynamic arrays or linked lists) by themselves. Priority queue can also be achieved. The interface is completely consistent, and the performance of different implementations at the bottom is different.
Array, entry O (1) complexity, maximum O (n) complexity when leaving the team. Linear Structure of Order Entry O(n) Exit O(1)
LeetCode Priority Queue Related Issues
Classical Question of Priority Queue: Choose the Top 100 out of 100000 Elements? Choose the Top M out of N Elements
The key is that M is much smaller than N; sorting, NlogN
Use priority queues: NlogM solves the problem. Use priority queues to maintain the first M elements currently seen, and replace them if the new element is larger than the smallest one. We need to use the smallest heap to quickly see the smallest of the first M elements. Continuously replace the smallest one in the previous M.
With the maximum heap, we can customize the size of the priority. (The smaller the value of the defined element, the higher the priority)
347 LeetCode https://leetcode-cn.com/problems/top-k-frequent-elements/description/
Firstly, the frequency of all elements is calculated, and then the first k height is calculated according to the frequency (Map).
package cn.mtianyan.leetcode_347; import cn.mtianyan.queue.PriorityQueue; import java.util.LinkedList; import java.util.List; import java.util.TreeMap; class Solution { private class Freq implements Comparable<Freq> { public int e, freq; public Freq(int e, int freq) { this.e = e; this.freq = freq; } /** * Define comparison rules, the lower the frequency, the higher the priority. * * @param another * @return */ @Override public int compareTo(Freq another) { if (this.freq < another.freq) return 1; else if (this.freq > another.freq) return -1; // If the current element is larger than the incoming element, return 1. This is normal and high priority. Let's reverse it here. else return 0; } } public List<Integer> topKFrequent(int[] nums, int k) { TreeMap<Integer, Integer> map = new TreeMap<>(); for (int num : nums) { if (map.containsKey(num)) map.put(num, map.get(num) + 1); else map.put(num, 1); } PriorityQueue<Freq> pq = new PriorityQueue<>(); for (int key : map.keySet()) { // I haven't saved enough k yet. if (pq.getSize() < k) pq.enqueue(new Freq(key, map.get(key))); // Replace the one with the smallest frequency else if (map.get(key) > pq.getFront().freq) { pq.dequeue(); pq.enqueue(new Freq(key, map.get(key))); } } LinkedList<Integer> res = new LinkedList<>(); while (!pq.isEmpty()) res.add(pq.dequeue().e); return res; } private static void printList(List<Integer> nums) { for (Integer num : nums) System.out.print(num + " "); System.out.println(); } public static void main(String[] args) { int[] nums = {1, 1, 1, 2, 2, 3}; int k = 2; printList((new Solution()).topKFrequent(nums, k)); } }
Operation results:
Using PriorityQueue in the java standard library
java's PriorityQueue internally defaults to a minimum heap.
public int compareTo(Freq another){ if(this.freq < another.freq) return -1; else if(this.freq > another.freq) return 1; else return 0; }
Our comparison of freq should follow the original size definition.
package cn.mtianyan.leetcode_347; import java.util.LinkedList; import java.util.List; import java.util.PriorityQueue; import java.util.TreeMap; public class SolutionOffical { private class Freq implements Comparable<Freq>{ public int e, freq; public Freq(int e, int freq){ this.e = e; this.freq = freq; } public int compareTo(Freq another){ if(this.freq < another.freq) return -1; else if(this.freq > another.freq) return 1; else return 0; } } public List<Integer> topKFrequent(int[] nums, int k) { TreeMap<Integer, Integer> map = new TreeMap<>(); for(int num: nums){ if(map.containsKey(num)) map.put(num, map.get(num) + 1); else map.put(num, 1); } PriorityQueue<Freq> pq = new PriorityQueue<>(); for(int key: map.keySet()){ if(pq.size() < k) pq.add(new Freq(key, map.get(key))); else if(map.get(key) > pq.peek().freq){ pq.remove(); pq.add(new Freq(key, map.get(key))); } } LinkedList<Integer> res = new LinkedList<>(); while(!pq.isEmpty()) res.add(pq.remove().e); return res; } private static void printList(List<Integer> nums){ for(Integer num: nums) System.out.print(num + " "); System.out.println(); } public static void main(String[] args) { int[] nums = {1, 1, 1, 2, 2, 3}; int k = 2; printList((new Solution()).topKFrequent(nums, k)); } }
Previously, in our own code, we set up a structure of our own: Freq implements Comparable < Freq>. To make it comparable, it is easy to specify its priority definition.
Many times what we want to change is the corresponding way of comparing classes in java standard libraries. PriorityQueue designed by ourselves is incompetent.
This PriorityQueue designed by Java provides us with a solution.
private class Freq { public int e, freq; public Freq(int e, int freq) { this.e = e; this.freq = freq; } } private class FreqComparator implements Comparator<Freq> { @Override public int compare(Freq a, Freq b) { return a.freq - b.freq; // You can write this for char int. } }
The FreqComparator class comparator implements the Comparator interface; overrides the compare method.
PriorityQueue<Freq> pq = new PriorityQueue<>(new FreqComparator());
Priority queues can be constructed by passing in comparators. The advantage of this writing is that in java, string objects are transmitted. Default dictionary order comparison. If you have your own custom string comparison scheme, define your own Comparator interface and pass it to the priority queue. We can also use this design for our own priority queue and its underlying implementation heap.
Because this FreqComparator will only be used for setting up the priority queue, only this time, you can use anonymous classes.
PriorityQueue<Freq> pq = new PriorityQueue<>(n1ew Comparator<Freq>() { @Override public int compare(Freq a, Freq b) { return a.freq - b.freq; } });
PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer a, Integer b) { return map.get(a) - map.get(b); } });
The comparison of integers in our algorithm is redefined as the comparison of key corresponding frequencies in map.
package cn.mtianyan.leetcode_347; /// 347. Top K Frequent Elements /// https://leetcode.com/problems/top-k-frequent-elements/description/ import java.util.*; public class SolutionIntegerCompareReDfine { public List<Integer> topKFrequent(int[] nums, int k) { TreeMap<Integer, Integer> map = new TreeMap<>(); for(int num: nums){ if(map.containsKey(num)) map.put(num, map.get(num) + 1); else map.put(num, 1); } PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer a, Integer b) { return map.get(a) - map.get(b); } }); for(int key: map.keySet()){ if(pq.size() < k) pq.add(key); else if(map.get(key) > map.get(pq.peek())){ pq.remove(); pq.add(key); } } LinkedList<Integer> res = new LinkedList<>(); while(!pq.isEmpty()) res.add(pq.remove()); return res; } private static void printList(List<Integer> nums){ for(Integer num: nums) System.out.print(num + " "); System.out.println(); } public static void main(String[] args) { int[] nums = {1, 1, 1, 2, 2, 3}; int k = 2; printList((new Solution()).topKFrequent(nums, k)); } }
PriorityQueue<Integer> pq = new PriorityQueue<>( Comparator.comparingInt(map::get) );// (a, b) -> map.get(a) - map.get(b)
Use java8 lambda expressions.
More topics related to heap
Our main implementation is binary heap. It is the easiest to expand into d-fork heap with lower layers.
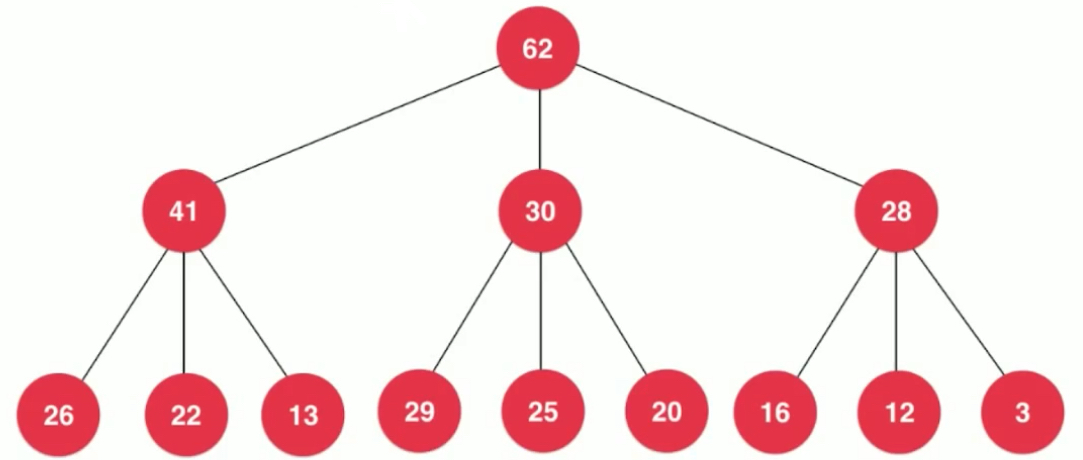
At the corresponding cost, there are more nodes to consider when sinking.
Our implementation can only see the heap head elements, and can not modify the elements of an index in the heap. Index heap is explained in the course of Algorithms and Data Structure. In Chapter 4, heap and heap sorting are discussed. Index heap is used to optimize graph theory.
Binomial Reactor and Fibonacci Reactor.
Generalized Queue: Priority Queue
Ordinary queue, priority queue, stack can also be understood as a queue.
The binary search tree is traversed by non-recursive preface and sequence. The basic logic is exactly the same. The difference is stack and queue. Logically consistent, data results are different. The algorithm visualizes the maze: the intrinsic relationship between depth and breadth, random queue.
The next chapter introduces segment trees.