The algorithm idea is the core to solve the problem. The tall buildings rise from the flat ground, which is also true in the algorithm. 95% of the algorithms are based on these six algorithm ideas. This paper introduces these six algorithm ideas to help you understand and solve various algorithm problems.

1 recursive algorithm

1.1 algorithm strategy

Recursive algorithm is an algorithm that directly or indirectly calls its own function or method.

The essence of recursive algorithm is to decompose the problem into subproblems of similar problems with reduced scale, and then recursively call methods to represent the solution of the problem. Recursive algorithm is very effective in solving a large class of problems. It can make the algorithm concise and easy to understand.

Advantages and disadvantages:

• Advantages: easy to implement
• Disadvantages: recursive algorithm is inefficient for common algorithms such as ordinary loop; And in the process of recursive call, the system opens up a stack for the return point and local quantity of each layer. The recursion is too deep, which is prone to stack overflow

1.2 applicable scenarios

Recursive algorithms are generally used to solve three types of problems:

• Data is defined recursively. (Fibonacci Series)
• The solution of the problem is realized by recursive algorithm. (backtracking)
• The structural form of data is defined recursively. (tree traversal, graph search)

Recursive problem solving strategy:

• Step 1: define the input and output of your function, regardless of the code in the function, but first understand what the input of your function is, what the output is, what the function is, and what kind of thing to accomplish.
• Step 2: find the end condition of recursion. We need to find out when the recursion ends, and then directly return the result
• Step 3: clarify the recursive relation and how to solve the current problem through various recursive calls

1.3 some classical problems solved by recursive algorithm

• Fibonacci sequence
• Hanoi Tower problem
• Tree traversal and related operations

DOM tree as an example

Next, take DOM as an example to implement a document Getelementbyid() function

Because DOM is a tree, and the definition of the tree itself is a recursive definition, it is very simple and natural to use the recursive method to deal with the tree.

Step 1: specify the input and output of your function

Recurse from the DOM root node layer by layer to determine whether the ID of the current node is the id='d-cal 'we are looking for

Input: DOM root node {document}, the} id='d-cal 'we are looking for

Output: returns the child node that satisfies {id='sisteran '

function getElementById(node, id){}

Step 2: find the end condition of recursion

Start with the document, and recursively find their child nodes for all child nodes, layer by layer:

• If the id of the current node meets the search criteria, the current node is returned
• If the leaf node has been reached and has not been found, null is returned

function getElementById(node, id){
    //The current node does not exist. It has reached the leaf node and has not been found yet. It returns null
    if(!node) return null
    //If the id {of the current node meets the search criteria, the current node is returned
    if(node.id === id) return node
}

Step 3: clarify the recursive relationship

The id of the current node does not meet the search conditions. Recursively search each of its child nodes

function getElementById(node, id){
    //The current node does not exist. It has reached the leaf node and has not been found yet. It returns null
    if(!node) return null
    //If the id {of the current node meets the search criteria, the current node is returned
    if(node.id === id) return node
    //The id ， of the previous node does not meet the search conditions. Continue to find each of its child nodes
    for(var i = 0; i < node.childNodes.length; i++){
        //Recursively find each of its child nodes
        var found = getElementById(node.childNodes[i], id);
        if(found) return found;
    }
    return null;
}

In this way, one of our documents The getelementbyid() function has been implemented:

function getElementById(node, id){
    if(!node) return null;
    if(node.id === id) return node;
    for(var i = 0; i < node.childNodes.length; i++){
        var found = getElementById(node.childNodes[i], id);
        if(found) return found;
    }
    return null;
}
getElementById(document, "d-cal");

Finally, verify on the console. The execution results are shown in the following figure:

The advantage of using recursion is that the code is easy to understand, but the disadvantage is that the efficiency is not as high as that of non recursive implementation. Chrome's DOM lookup is implemented using non recursive methods. How to implement non recursion?

The following code:

function getByElementId(node, id){
    //Traverse all nodes
    while(node){
        if(node.id === id) return node;
        node = nextElement(node);
    }
    return null;
}

It still traverses all DOM nodes in turn, but this time it is changed to a while loop, and the function nexterelement is responsible for finding the next node. Therefore, the key lies in how this {nexterelement} implements the function of non recursive node lookup:

//Depth traversal
function nextElement(node){
    //First judge whether there are child nodes
    if(node.children.length) {
        //If yes, the first child node is returned
        return node.children[0];
    }
    //Then judge whether there are adjacent nodes
    if(node.nextElementSibling){
        //If yes, it returns its next adjacent node
        return node.nextElementSibling;
    }
    //Otherwise, the next adjacent element of its parent node is returned upward, which is equivalent to i plus 1 of the for loop in the recursive implementation above
    while(node.parentNode){
        if(node.parentNode.nextElementSibling) {
            return node.parentNode.nextElementSibling;
        }
        node = node.parentNode;
    }
    return null;
}

Running this code in the console can also output the results correctly. Whether non recursive or recursive, they are depth first traversal, as shown in the following figure.

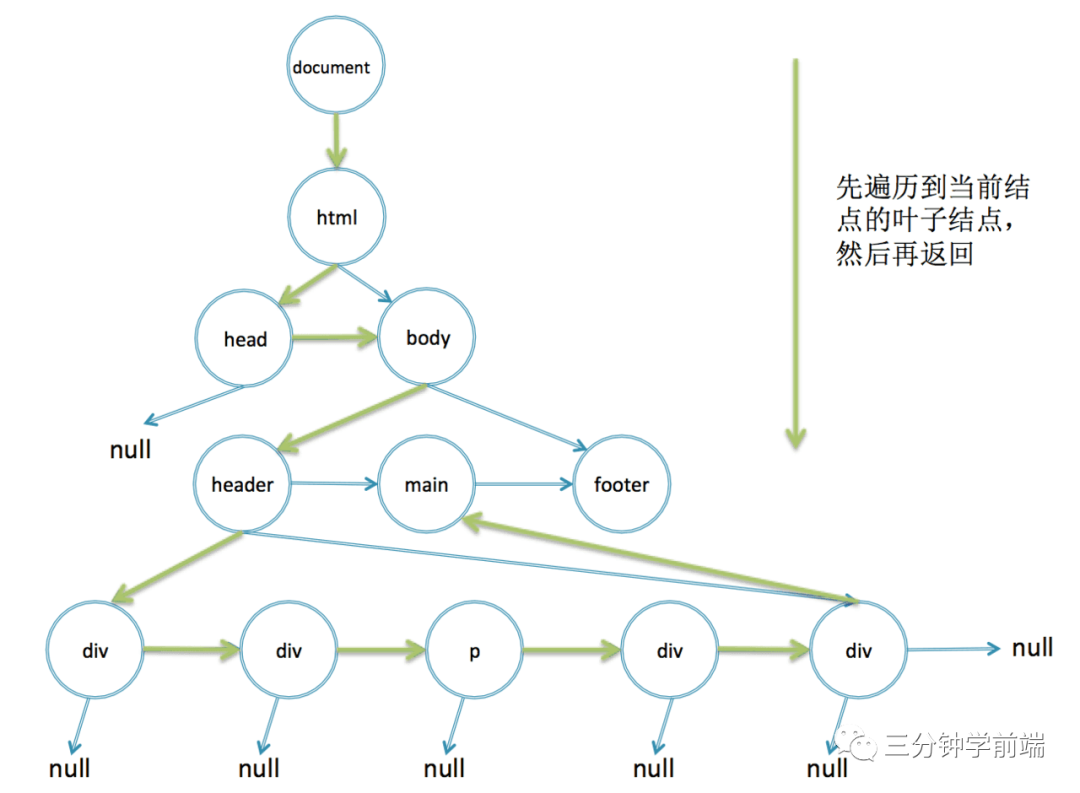
In fact, the getElementById browser is stored in a hash map, which is directly mapped to the DOM node according to the id, and getelementbyclassname uses such non recursive search.

Reference: front end data structures and algorithms I've been in contact with

2 divide and conquer algorithm

2.1 algorithm strategy

In computer science, divide and conquer algorithm is a very important algorithm. Quick sorting and merge sorting are implemented based on divide and conquer strategy. Therefore, it is recommended to understand and master it.

Divide and conquer, as the name suggests, is to divide and conquer a complex problem into two or more similar subproblems, and divide the subproblem into smaller subproblems until the smaller subproblem can be solved simply. If the subproblem is solved, the solution of the original problem is the combination of the solutions of a subproblem.

2.2 applicable scenarios

When a problem meets the following conditions, you can try to solve it only by divide and conquer strategy:

• The original problem can be divided into several similar subproblems
• Subproblems can be easily solved
• The solution of the original problem is the combination of the solutions of the subproblems
• Each subproblem is independent of each other and does not contain the same subproblem

Problem solving strategy of divide and Conquer:

• Step 1: decomposition: decompose the original problem into several small-scale, independent sub problems with the same form as the original problem
• Step 2: solve all sub problems
• Step 3: merge the solutions of each sub problem into the solutions of the original problem

2.3 some classical problems solved by divide and conquer method

• Binary search
• Merge sort
• Quick sort
• Hanoi Tower problem
• React time slice

Binary search

Also known as half search algorithm, it is a simple and easy to understand fast search algorithm. For example, I randomly write a number between 0 and 100. Let you guess what I wrote? Every time you guess, I'll tell you whether it's big or small until you get it right.

Step 1: decomposition

Each time, the results of the last guess are divided into a large group and a small group. The two groups are independent of each other

• Select the middle number in the array

function binarySearch(items, item) {
    //low, mid, high divide the array into two groups
    var low = 0,
        high = items.length - 1,
        mid = Math.floor((low+high)/2),
        elem = items[mid]
    // ...
}

Step 2: solve the sub problem

Comparison between search number and middle number

• If it is lower than the middle number, look in the subarray to the left of the middle number;
• If it is higher than the middle number, look in the subarray to the right of the middle number;
• If equal, the search is returned successfully

while(low <= high) {
 if(elem < item) { //Higher than the middle number
  low = mid + 1
 } else if(elem > item) { //Lower than the middle number
  high = mid - 1
 } else { //Equal
     return mid
 }
}

Step 3: Merge

function binarySearch(items, item) {
    var low = 0,
        high = items.length - 1,
        mid, elem
    while(low <= high) {
        mid = Math.floor((low+high)/2)
        elem = items[mid]
        if(elem < item) {
            low = mid + 1
        } else if(elem > item) {
            high = mid - 1
        } else {
            return mid
        }
    }
    return -1
}

Finally, dichotomy can only be applied to the case of array order. If the array is out of order, dichotomy search will not work

function binarySearch(items, item) {
    //Quick row
    quickSort(items)
    var low = 0,
        high = items.length - 1,
        mid, elem
    while(low <= high) {
        mid = Math.floor((low+high)/2)
        elem = items[mid]
        if(elem < item) {
            low = mid + 1
        } else if(elem > item) {
            high = mid - 1
        } else {
            return mid
        }
    }
    return -1
}

//Testing
var arr = [2,3,1,4]
binarySearch(arr, 3)
// 2

binarySearch(arr, 5)
// -1

Test successful

3 greedy algorithm

3.1 algorithm strategy

Greedy algorithm, hence its name, always makes the current optimal choice, hoping to obtain the overall optimal choice through local optimal choice.

In a sense, greedy algorithm is very greedy and short-sighted. It does not consider the whole and only focuses on the current best interests. Therefore, its choice is only local optimization in a sense, but greedy algorithm can still get the optimal solution or better solution on many problems, so its existence is still meaningful.

3.2 applicable scenarios

In daily life, we often use greedy algorithms, such as:

How can you get the most value by taking out 10 notes from 100 pieces of banknotes with different denominations?

We only need to select the largest face value of the remaining banknotes every time, and finally we must get the optimal solution, which is the greedy algorithm used, and finally we get the overall optimal solution.

However, we still need to make it clear that the expectation to obtain the overall optimal choice through the local optimal choice is only the expectation, and the final result may not necessarily be the overall optimal solution.

For example: find the shortest path from A to G:

According to the greedy algorithm, the current optimal choice is always selected, so the first path it selects is AB, then BE and EG. the total length of the path is 1 + 5 + 4 = 10. However, this is not the shortest path. The shortest path is a - > C - > G: 2 + 2 = 4. Therefore, the greedy algorithm does not necessarily get the optimal solution.

So when can I try to use greedy algorithm?

When the following conditions are met, you can use:

• The complexity of the original problem is too high
• The mathematical model for finding the global optimal solution is difficult to establish or the amount of calculation is too large
• There is not much need to require a global optimal solution, "better" is OK

If the greedy algorithm is used to find the optimal solution, it can be solved according to the following steps:

• First, we need to clarify what is the optimal solution (expectation)
• Then, divide the problem into multiple steps, and each step needs to meet:
•  
  • Feasibility: each step satisfies the constraints of the problem
•  
  • Local optimization: make a local optimal choice at each step
• -Cannot cancel: once the selection is made, it cannot be cancelled under any subsequent circumstances
• Finally, the optimal solution of all steps is the global optimal solution

3.3 classic case: activity selection

Classical problems solved by greedy algorithm include:

• Minimum spanning tree algorithm
• Dijkstra algorithm for single source shortest path
• Huffman compression coding
• knapsack problem
• Activity selection questions, etc

The activity selection problem is the simplest, which is described in detail here.

The activity selection problem is an example in the introduction to algorithms, and it is also a very classic problem. There are n activities (a1,a2,..., an) that need to use the same resource (such as classroom), and the resource can only be used by one activity at a certain time. Each activity ai has a start time si and an end time fi. Once selected, the activity ai occupies a half open time interval [si,fi). If [si,fi) and [sj,fj) do not overlap each other, ai and aj can be arranged on this day.

The problem is to arrange these activities so that as many activities as possible can be held without conflict. For example, the activity set S shown in the figure below, in which the activities are sorted monotonically and incrementally according to the end time.

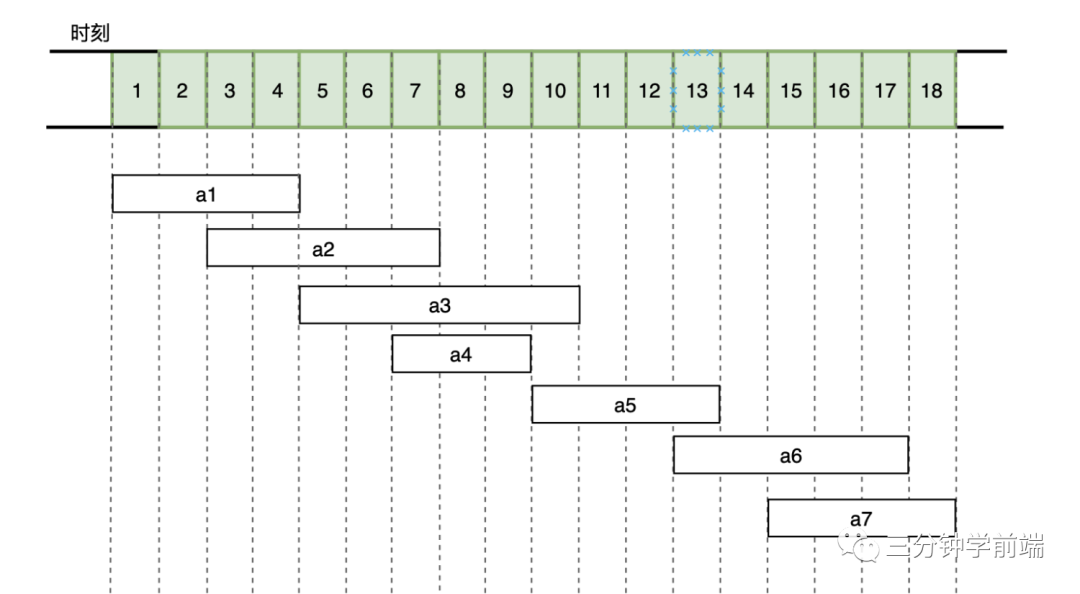
There are 7 activities in total. The time they need to occupy within 18 hours is shown in the figure above. How to select activities to maximize the utilization of this classroom (more activities can be held)?

The greedy algorithm is very simple to solve this problem. It starts to select at the start time. Each time it selects the activities whose start time does not conflict with the selected activities, and whose end time is relatively high, it will make the remaining time interval longer.

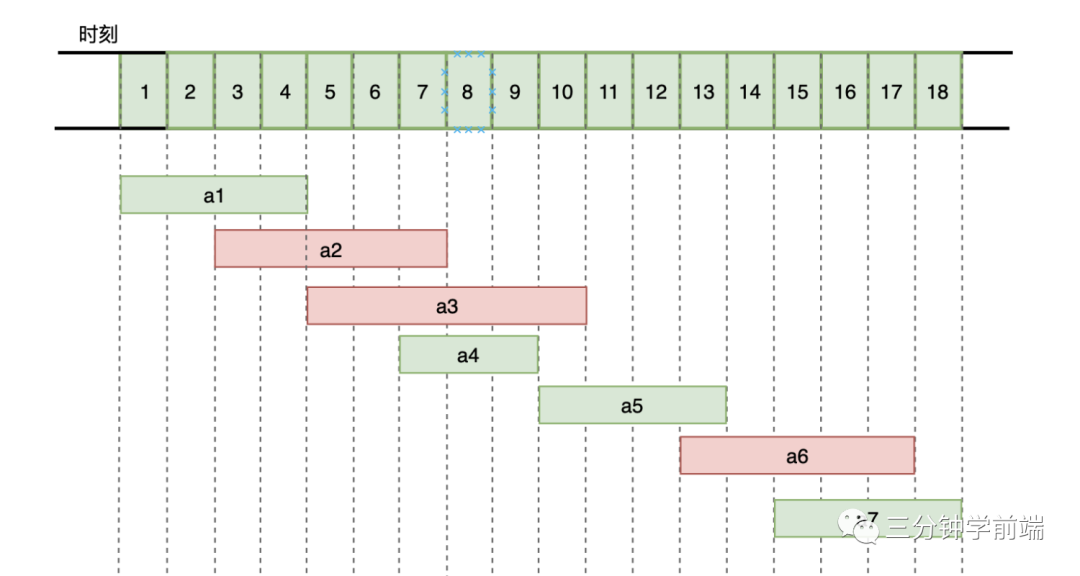
• First, the end time of a1 activity is the earliest. Select a1 activity
• After a1 ends, a2 has a time conflict and cannot be selected. Both a3 and a4 can be selected, but a4 ends the earliest. Select a4
• Select the activities with no time conflict and the earliest end time in turn

The final selection activities are a1, a4, a5, a7. Is the optimal solution.

4 backtracking algorithm

4.1 algorithm strategy

Backtracking algorithm is a search method, heuristic method. It will make a choice at each step. Once it is found that the choice cannot get the expected result, it will backtrack and make a choice again. Depth first search uses the idea of backtracking algorithm.

4.2 applicable scenarios

The backtracking algorithm is very simple. It just keeps trying until it gets the solution. Its algorithmic idea makes it usually used to solve the breadth search problem, that is, select a solution that meets the requirements from a set of possible solutions.

4.3 classic cases of using backtracking algorithm

• Depth first search
• 0-1 knapsack problem
• Regular Expression Matching
• Eight queens
• Sudoku
• Full arrangement

Wait, depth first search has been introduced in the figure chapter. Here, take regular expression matching as an example

Regular Expression Matching

var string = "abbc"

var regex = /ab{1,3}c/

console.log( string.match(regex) )

// ["abbc", index: 0, input: "abbc", groups: undefined]

Its matching process:

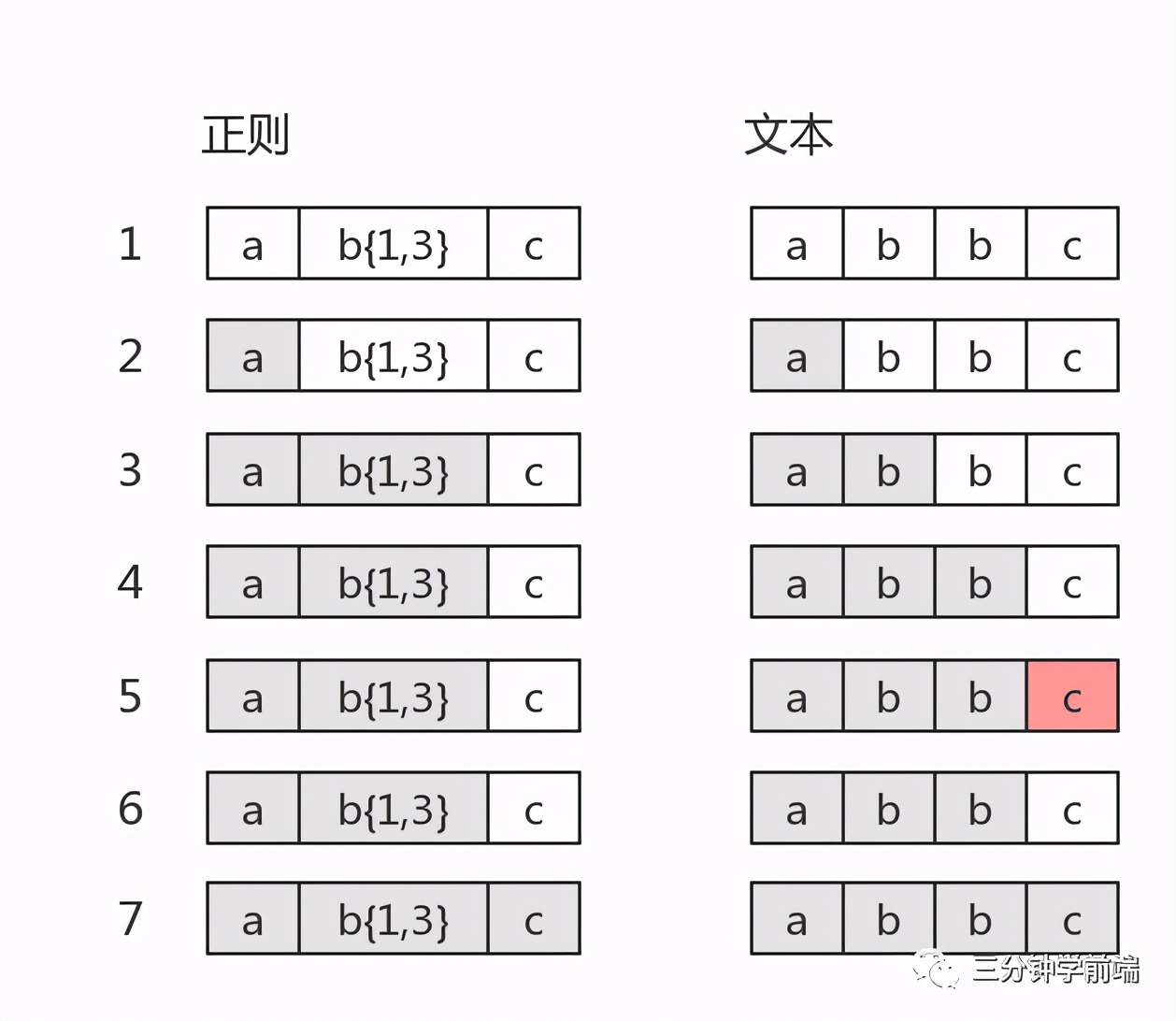
In step 5, the matching fails. At this time, {b{1,3} has been matched to two} b. the third} b is being tried, and it is found that the next is} c. At this time, you need to go back to the previous step, b{1,3} matching is completed (matching to} bb), and then match {c, matching to {c} matching is completed.

5 dynamic programming

5.1 algorithm strategy

Dynamic programming is also a strategy to decompose complex problems into small problems. Different from divide and conquer algorithm, divide and conquer algorithm requires each sub problem to be independent of each other, while each sub problem of dynamic programming is interrelated.

Therefore, dynamic programming is applicable to the case of overlapping subproblems, that is, different subproblems have common subproblems. In this case, the divide and conquer strategy will do a lot of unnecessary work. It will repeatedly solve those common subproblems, while dynamic programming will solve each subproblem once and then save it in the table. If consistent problems are encountered, It can be obtained from the table, so it does not need to solve each sub problem and avoids a large number of unnecessary operations.

5.2 applicable scenarios

Dynamic programming is suitable for solving the optimal solution problem. For example, arbitrarily select multiple coins from 100 coins of variable denomination to make up 10 yuan. Find out how to select coins to minimize the number of coins finally selected and just make up 10 yuan. This is a typical dynamic programming problem. It can be divided into a sub problem (each coin selection), and each sub problem has a common sub problem (coin selection). The sub problems are interrelated (the total amount of coins selected cannot exceed 10 yuan), and the boundary condition is that the total amount of coins finally selected is 10 yuan.

For the above example, maybe you can also say that we can use the backtracking algorithm to constantly explore, but the backtracking algorithm uses the solution with the breadth of solution (the solution that meets the requirements). If we use the backtracking algorithm, we need to try to find all the solutions that meet the conditions, and then find the optimal solution. The time complexity is O(2^n ^), which is quite poor. Most problems suitable for dynamic programming can use backtracking algorithm, but the time complexity of backtracking algorithm is relatively high.

Finally, to sum up, we need to follow the following important steps when using dynamic programming to solve problems:

• Define subproblems
• Implement the sub problem parts that need to be solved repeatedly
• Identify and solve the boundary conditions

5.3 some classical problems solved by dynamic programming

• Stair climbing problem: suppose you are climbing stairs. You need n steps to reach the roof. You can climb one or two steps at a time. How many different ways can you climb to the roof?
• Knapsack problem: give some resources (total amount and value), give a knapsack (total capacity), and load resources into the knapsack. The goal is to load more value when the knapsack does not exceed the total capacity
• Coin change: give a certain amount of change with variable denomination and the amount of change required, and find out how many change schemes there are
• All source shortest path of a graph: a graph contains u and V vertices, and find the shortest path from vertex u to vertex v
• Longest common subsequence: find the longest common subsequence of a group of sequences (you can delete elements from another sequence without changing the order of the remaining elements)

Take the longest common subsequence as an example.

Stair climbing problem

Taking the classical problem of dynamic programming stair climbing problem as an example, this paper introduces the steps to solve the dynamic programming problem.

Step 1: define subproblems

If ＾ dp[n] is used to represent the number of schemes of step ＾ n, and it is known from the title that the last step may take two steps or one step, that is, the number of schemes of step ＾ n is equal to the number of schemes of step ＾ n-1 ＾ plus the number of schemes of step ＾ n-2 ＾

Step 2: implement the sub problem parts that need to be solved repeatedly

dp[n] = dp[n−1] + dp[n−2]

Step 3: identify and solve the boundary conditions

//Level 0 # 1 # scheme
dp[0]=1 
//Level 1 # is also a # 1 # scheme
dp[1]=1

The last step: translate the tail code into code and deal with some boundary conditions

let climbStairs = function(n) {
    let dp = [1, 1]
    for(let i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n]
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(n)

Optimize space complexity:

let climbStairs = function(n) {
    let res = 1, n1 = 1, n2 = 1
    for(let i = 2; i <= n; i++) {
        res = n1 + n2
        n1 = n2
        n2 = res
    }
    return res
}

Space complexity: O(1)

6 enumeration algorithm

6.1 algorithm strategy

The idea of enumeration algorithm is to list all possible answers to the problem one by one, and then judge whether the answer is appropriate according to the conditions, retain the appropriate and discard the inappropriate.

6.2 problem solving ideas

• Determine the enumeration object, enumeration range and judgment conditions.
• List the possible solutions one by one to verify whether each solution is the solution of the problem.

7 brush questions

7.1 stair climbing

Suppose you are climbing stairs. You need n steps to reach the roof.

You can climb one or two steps at a time. How many different ways can you climb to the roof?

Note: given n is a positive integer.

Example 1:

Input: 2
 Output: 2
 Explanation: There are two ways to climb to the roof.
1. 1 rank + 1 rank
2. 2 rank

Example 2:

Input: 3
 Output: 3
 Explanation: There are three ways to climb to the roof.
1. 1 rank + 1 rank + 1 rank
2. 1 rank + 2 rank
3. 2 rank + 1 rank

Solution: dynamic programming

Dynamic Programming (DP) is a strategy to decompose complex problems into small problems, but different from the divide and conquer algorithm, the divide and conquer algorithm requires each sub problem to be independent of each other, while the sub problems of Dynamic Programming are interrelated.

Divide and conquer, as the name suggests, is to divide and conquer. A complex problem is divided into two or more similar subproblems. The subproblem is divided into smaller subproblems until the smaller subproblem can be solved simply. If the subproblem is solved, the solution of the original problem is the combination of subproblem solutions.

When we use dynamic programming to solve problems, we need to follow the following important steps:

• Define subproblems
• Implement the sub problem parts that need to be solved repeatedly
• Identify and solve the boundary conditions

Step 1: define subproblems

If ＾ dp[n] is used to represent the number of schemes of step ＾ n, and it is known from the title that the last step may take two steps or one step, that is, the number of schemes of step ＾ n is equal to the number of schemes of step ＾ n-1 ＾ plus the number of schemes of step ＾ n-2 ＾

Step 2: implement the sub problem parts that need to be solved repeatedly

dp[n] = dp[n−1] + dp[n−2]

Step 3: identify and solve the boundary conditions

//Level 0 # 1 # scheme
dp[0]=1 
//Level 1 is also a scheme
dp[1]=1

The last step: translate the tail code into code and deal with some boundary conditions

let climbStairs = function(n) {
    let dp = [1, 1]
    for(let i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n]
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(n)

Optimize space complexity:

let climbStairs = function(n) {
    let res = 1, n1 = 1, n2 = 1
    for(let i = 2; i <= n; i++) {
        res = n1 + n2
        n1 = n2
        n2 = res
    }
    return res
}

Space complexity: O(1)

More answers

7.2 climbing stairs with minimum cost

Each index of the array is used as a ladder, and the ＾ I ＾ ladder corresponds to a non negative physical cost value ＾ cost[i] (the index starts from 0).

Every time you climb a ladder, you have to spend the corresponding physical cost, and then you can choose to continue climbing one ladder or two.

You need to find the lowest cost to reach the top of the floor. At the beginning, you can choose the element with index 0 or 1 as the initial ladder.

Example 1:

input: cost = [10, 15, 20]
output: 15
 explain: The minimum cost is from cost[1]Start, and then take two steps to the top of the ladder. It costs a total of 15.

Example 2:

input: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
output: 6
 explain: The lowest cost is from cost[0]Start, go through those ones one by one, skip cost[3]，The total cost is 6.

be careful:

• The length of cost ， will be [2, 1000].
• Each cost[i] will be an Integer type with a range of [0, 999].

Solution: dynamic programming

Please understand the meaning of this question:

• The ＾ step is the top of the ＾ i-1 ＾ step.
• It costs ， cost[i] to step on the ， I ， I ， and it doesn't cost to take a big step without stepping up.
• The top of the stairs is outside the array. If the array length is ， len, the roof is subscript ， len

Step 1: define subproblems

The physical consumption of stepping on the # th step is the minimum physical consumption of the first two steps plus the physical consumption of this layer:

• Finally, take one step and step on the {I} step: dp[i-1] + cost[i]
• Finally, take one step and step on the {I} step: dp[i-2] + cost[i]

Step 2: implement the sub problem parts that need to be solved repeatedly

Therefore, the minimum cost of stepping on the # th step is:

dp[i] = min(dp[i-2], dp[i-1]) + cost[i]

Step 3: identify and solve the boundary conditions

//Level 0 # cost[0] scheme
dp[0] = cost[0]
//At level # 1 # there are two cases
// 1: It costs cost cost[0] + cost[1] to step on step 0 and step 1 respectively
// 2: Take two steps directly from the ground to the first step, and cost[1]
dp[1] = min(cost[0] + cost[1], cost[1]) = cost[1]

The last step: translate the tail code into code and deal with some boundary conditions

let minCostClimbingStairs = function(cost) {
    cost.push(0)
    let dp = [], n = cost.length
    dp[0] = cost[0]
    dp[1] = cost[1]
    for(let i = 2; i < n; i++){
        dp[i] = Math.min(dp[i-2] , dp[i-1]) + cost[i]
    }
    return dp[n-1]
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(n)

Optimization:

let minCostClimbingStairs = function(cost) {
    let n = cost.length,
        n1 = cost[0],
        n2 = cost[1] 
    for(let i = 2;i < n;i++){
        let tmp = n2
        n2 = Math.min(n1,n2)+cost[i]
        n1 = tmp
    }
    return Math.min(n1,n2)
};

• Time complexity: O(n)
• Space complexity: O(1)

More answers

7.3 maximum subsequence sum

Given an integer array {nums, find a continuous subarray with the largest sum (the subarray contains at least one element) and return its maximum sum.

Example:

input: [-2,1,-3,4,-1,2,1,-5,4]
output: 6
 explain: Continuous subarray [4,-1,2,1] The sum of the maximum is 6. 

Advanced:

If you have implemented a solution with complexity O(n), try using a more sophisticated divide and conquer method.

Step 1: define subproblems

Dynamic programming is to summarize and consider the whole array. Assuming that we already know the maximum sum of continuous subarrays ending with the ＾ i-1 ＾ dp[i-1], it is obvious that the possible value of the maximum sum of continuous subarrays ending with the i-th number is either ＾ dp[i-1]+nums[i], or ＾ nums[i] in a separate group, that is, ＾ nums[i]. In these two numbers, we take the maximum value

Step 2: implement the sub problem parts that need to be solved repeatedly

dp[n] = Math.max(dp[n−1]+nums[n], nums[n])

Step 3: identify and solve the boundary conditions

dp[0]=nums[0]

The last step: translate the tail code into code and deal with some boundary conditions

When calculating dp[i], we only care about dp[i-1] and [num [i], so we don't need to save the whole dp array, just set a pre dp[i-1].

Code implementation (optimization):

let maxSubArray = function(nums) {
    let max = nums[0], pre = 0
    for(const num of nums) {
        if(pre > 0) {
            pre += num
        } else {
            pre = num
        }
        max = Math.max(max, pre)
    }
    return max
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(1)

More answers

7.4 the best time to buy and sell stocks

Given an array, its i-th element is the price of a given stock on day I.

If you are allowed to complete only one transaction at most (i.e. buy and sell a stock once), design an algorithm to calculate the maximum profit you can make.

Note: you cannot sell stocks before you buy them.

Example 1:

input: [7,1,5,3,6,4]
output: 5
 explain: In the first 2 Days (stock price) = 1)When buying, in the second 5 Days (stock price) = 6)When you sell, you make the most profit = 6-1 = 5 . 
     Note that profits cannot be 7-1 = 6, Because the selling price needs to be greater than the buying price; At the same time, you can't sell stocks before buying.

Example 2:

input: [7,6,4,3,1]
output: 0
 explain: under these circumstances, No transaction completed, So the maximum profit is 0. 

Solution: dynamic programming

Step 1: define subproblems

Dynamic programming is to summarize and consider the whole array. Assuming that we already know that the maximum profit of ＾ i-1 ＾ stocks is ＾ dp[i-1], it is obvious that the maximum profit of ＾ I ＾ continuous stocks is ＾ dp[i-1], or ＾ prices[i] - minprice (minprice ＾ is the minimum value of the first ＾ i-1 ＾ stocks), we take the maximum value in these two numbers

Step 2: implement the sub problem parts that need to be solved repeatedly

dp[i] = Math.max(dp[i−1], prices[i] - minprice)

Step 3: identify and solve the boundary conditions

dp[0]=0

The last step: translate the tail code into code and deal with some boundary conditions

Because we only care about {dp[i-1] and} prices[i] when calculating} dp[i], we don't need to save the whole} dp} array, just set a} max} to save} dp[i-1].

Code implementation (optimization):

let maxProfit = function(prices) {
    let max = 0, minprice = prices[0]
    for(let i = 1; i < prices.length; i++) {
        minprice = Math.min(prices[i], minprice)
        max = Math.max(max, prices[i] - minprice)
    }
    return max
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(1)

More answers

7.5 palindrome substring

Given a string, your task is to calculate how many palindrome substrings there are in the string.

Substrings with different start or end positions, even if they are composed of the same characters, will be regarded as different substrings.

Example 1:

Input:"abc"
Output: 3
 Explanation: three palindrome substrings: "a", "b", "c"

Example 2:

Input:"aaa"
Output: 6
 Explanation: 6 palindrome substrings: "a", "a", "a", "aa", "aa", "aaa"

Tips:

• The length of the input string will not exceed 1000.

Solution 1: Violence Law

let countSubstrings = function(s) {
  let count = 0
  for (let i = 0; i < s.length; i++) {
    for (let j = i; j < s.length; j++) {
      if (isPalindrome(s.substring(i, j + 1))) {
        count++
      }
    }
  }
  return count
}

let isPalindrome = function(s) {
  let i = 0, j = s.length - 1
  while (i < j) {
    if (s[i] != s[j]) return false
    i++
    j--
  }
  return true
}

Complexity analysis:

• Time complexity: O(n^3 ^)
• Space complexity: O(1)

Solution 2: dynamic programming

A string is a palindrome string, its beginning and end characters are the same, and the remaining substring is also a palindrome string. Among them, whether the remaining substring is a palindrome string is a smaller sub problem, and its result affects the result of the big problem.

How do we describe the sub problem?

Obviously, a substring is determined by the {I, j} pointers at both ends, which is the variable describing the sub problem. Whether the substring} s[i...j] (dp[i][j]) is a palindrome string is the sub problem.

We use a two-dimensional array to record the results of the calculated subproblems. Starting from the base case, we recurs the solution of each subproblem like filling in a table.

    j
    a  a  b  a
i a ✅
  a    ✅  
  b       ✅
  a          ✅

Note: I < = J, only half of the table is needed for vertical scanning

So:

i === j: dp[i][j]=true
j - i == 1 && s[i] == s[j]: dp[i][j] = true
j - i > 1 && s[i] == s[j] && dp[i + 1][j - 1]: dp[i][j] = true

Namely:

s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1]): dp[i][j]=true

Otherwise, it is false

Code implementation:

let countSubstrings = function(s) {
  const len = s.length
  let count = 0
  const dp = new Array(len)

  for (let i = 0; i < len; i++) {
    dp[i] = new Array(len).fill(false)
  }
  for (let j = 0; j < len; j++) {
    for (let i = 0; i <= j; i++) {
      if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
        dp[i][j] = true
        count++
      } else {
        dp[i][j] = false
      }
    }
  }
  return count
}

Code implementation (optimization):

If the vertical column of the table in the figure above is regarded as a one-dimensional array or a vertical scan, you only need to define {dp} as a one-dimensional array

let countSubstrings = function(s) {
  const len = s.length
  let count = 0
  const dp = new Array(len)

  for (let j = 0; j < len; j++) {
    for (let i = 0; i <= j; i++) {
      if (s[i] === s[j] && (j - i <= 1 || dp[i + 1])) {
        dp[i] = true
        count++
      } else {
        dp[i] = false
      }
    }
  }
  return count;
}

Complexity analysis:

• Time complexity: O(n^2 ^)
• Space complexity: O(n)

More answers

7.6 longest palindrome substring

Given a string s, find the longest palindrome substring in S. You can assume that the maximum length of S is 1000.

Example 1:

input: "babad"
output: "bab"
be careful: "aba" It is also an effective answer.

Example 2:

input: "cbbd"
output: "bb"

Solution: dynamic programming

Step 1: define status

dp[i][j] indicates whether the substring {s[i..j] is a palindrome substring. Here, the substring} s[i..j] is defined as a left closed and right closed interval, which can take} s[i] and} s[j].

Step 2: think about the state transition equation

For a substring, if it is a palindrome string, add the same character at the beginning and end of it, and it is still a palindrome string

dp[i][j] = (s[i] === s[j]) && dp[i+1][j-1]

Step 3: initial state:

dp[i][i] = true //A single character is a palindrome string
if(s[i] === s[i+1]) dp[i][i+1] = true //Two consecutive identical characters are palindromes

Code implementation:

const longestPalindrome = (s) => {
  if (s.length < 2) return s
  //res: Longest palindrome substring
  let res = s[0], dp = []
  for (let i = 0; i < s.length; i++) {
    dp[i][i] = true
  }
  for (let j = 1; j < s.length; j++) {
    for (let i = 0; i < j; i++) {
      if (j - i === 1 && s[i] === s[j]) {
        dp[i][j] = true
      } else if (s[i] === s[j] && dp[i + 1][j - 1]) {
        dp[i][j] = true
      }   
      //Gets the current longest palindrome substring
      if (dp[i][j] && j - i + 1 > res.length) {
        res = s.substring(i, j + 1)
      }
    }
  }

  return res
}

Complexity analysis:

• Time complexity: O(n^2 ^)
• Space complexity: O(n^2 ^)

More answers

7.7 minimum path and

Given a {m x n} grid containing non negative integers, find a path from the upper left corner to the lower right corner so that the sum of numbers on the path is the smallest.

Note: you can only move down or right one step at a time.

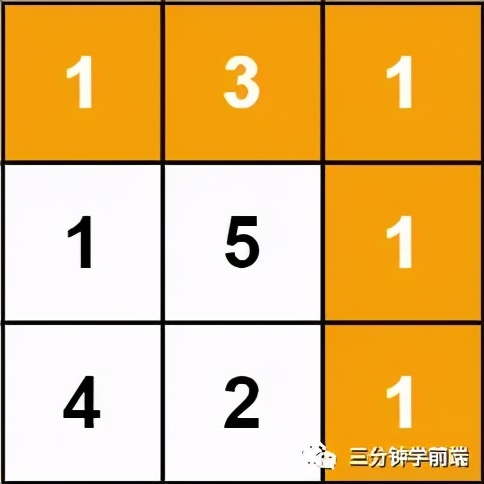
Example 1:

Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
 Explanation: because path 1→3→1→1→1 The sum of is the smallest.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

Tips:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

1. DP equation ， minimum path sum of current term = current term value + minimum value in previous term or left term ， grid [i] [J] + = math min( grid[i - 1][j], grid[i][j - 1] )

2. The first row and the first column of the boundary processing grid have no upper item and left item respectively, so the minimum path of the item and the first row are calculated separately:

for(let j = 1; j < col; j++) grid[0][j] += grid[0][j - 1]

Calculate the first column:

for(let i = 1; i < row; i++) grid[i][0] += grid[i - 1][0]

3. Code implementation

var minPathSum = function(grid) {
    let row = grid.length, col = grid[0].length

    // calc boundary
    for(let i = 1; i < row; i++)
        // calc first col
        grid[i][0] += grid[i - 1][0]

    for(let j = 1; j < col; j++)
        // calc first row
        grid[0][j] += grid[0][j - 1]

    for(let i = 1; i < row; i++)
        for(let j = 1; j < col; j++)
            grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1])
    
    return grid[row - 1][col - 1]
};

More answers

7.8 best time to buy and sell stocks II

Given an array, its i-th element is the price of a given stock on day I.

Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buying and selling a stock multiple times).

Note: you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).

Example 1:

input: [7,1,5,3,6,4]
output: 7
 explain: In the first 2 Days (stock price) = 1)When buying, in the second 3 Days (stock price) = 5)Sell at, The exchange is profitable = 5-1 = 4 . 
     Subsequently, on page 4 Days (stock price) = 3)When buying, in the second 5 Days (stock price) = 6)Sell at, The exchange is profitable = 6-3 = 3 . 

Example 2:

input: [1,2,3,4,5]
output: 4
 explain: In the first 1 Days (stock price) = 1)When buying, in the second 5 day (Stock price = 5)Sell at, The exchange is profitable = 5-1 = 4 . 
     Note that you can't be in the first place 1 Days and days 2 Buy stocks one day after another and then sell them.
     Because you are involved in multiple transactions at the same time, you must sell the previous shares before buying again.

Example 3:

input: [7,6,4,3,1]
output: 0
 explain: under these circumstances, No transaction completed, So the maximum profit is 0. 

Tips:

• 1 <= prices.length <= 3 * 10 ^ 4
• 0 <= prices[i] <= 10 ^ 4

Solution 1: buy at the peak and sell at the peak

As shown in the figure, buying on the second day, selling on the third day, buying on the fourth day and selling on the fifth day have the highest profit. The code here will not be repeated. You can try to write it yourself

Solution 2: greedy algorithm

Greedy algorithm, hence its name, always makes the current optimal choice, hoping to obtain the overall optimal choice through local optimal choice.

In a sense, greedy algorithm is very greedy and short-sighted. It does not consider the whole and only focuses on the current best interests. Therefore, its choice is only local optimization in a sense, but greedy algorithm can still get the optimal solution or better solution on many problems, so its existence is still meaningful.

Corresponding to this question, buy on the first day, sell on the second day,..., buy on the... i day and sell on the... i+1 day. If you buy on the... i day and sell on the... i+1 day, you will buy if there is a profit, otherwise you will not buy

Buy on the ， i-1 ， sell on the ， I ， I ， I ， I ， I ， I ， I ， I ， I ， I ， I ， I ， I

Code implementation:

let maxProfit = function(prices) {
    let profit = 0
    for (let i = 0; i < prices.length - 1; i++) {
        if (prices[i + 1] > prices[i]) {
            profit += prices[i + 1] - prices[i]
        }
    }
    return profit
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(1)

More answers

7.9 distribution of biscuits

Suppose you are a great parent and want to give your children some cookies. However, each child can only give one biscuit at most. For each child I, there is an appetite value g~i~, which is the minimum size of biscuits that can satisfy the children's appetite; And every cookie J has a size s~j~. If s ~ J ~ > = G ~ I ~, we can distribute the biscuit J to child I, and the child will be satisfied. Your goal is to meet as many children as possible and output this maximum value.

be careful:

You can assume a positive appetite. A child can only have one cookie at most.

Example 1:

input: [1,2,3], [1,1]

output: 1

explain: 
You have three children and two biscuits. The appetite values of the three children are: 1,2,3. 
Although you have two small biscuits, because their size is 1, you can only satisfy children with an appetite of 1.
So you should output 1.

Example 2:

input: [1,2], [1,2,3]

output: 2

explain: 
You have two children and three cookies. The appetite values of two children are 1,2. 
You have enough cookies and sizes to satisfy all children.
So you should output 2.

Solution: greedy algorithm

const findContentChildren = (g, s) => {
    if (!g.length || !s.length) return 0
    
    g.sort((a, b) => a - b)
    s.sort((a, b) => a - b)
    
    let gi = 0, si = 0
    while (gi < g.length && si < s.length) {
        if (g[gi] <= s[si++]) gi++
    }
    return gi
}

More answers

7.10 split array into continuous subsequences

Give you an integer array {num (which may contain duplicate numbers) sorted in ascending order. Please divide them into one or more subsequences, where each subsequence is composed of continuous integers and has a length of at least 3.

If the above segmentation can be completed, return {true; Otherwise, false is returned.

Example 1:

input: [1,2,3,3,4,5]
output: True
 explain:
You can segment such two consecutive subsequences : 
1, 2, 3
3, 4, 5

Example 2:

input: [1,2,3,3,4,4,5,5]
output: True
 explain:
You can segment such two consecutive subsequences : 
1, 2, 3, 4, 5
3, 4, 5

Example 3:

input: [1,2,3,4,4,5]
output: False

Tips:

• The input array length range is [1, 10000]

Solution: greedy algorithm

From the beginning, we only look for the sequence that meets the conditions each time (the length of the continuous subsequence is 3). After elimination, we traverse back in turn:

• Judge whether the current element can be spliced to the previous continuous subsequence that meets the conditions. If so, splice
• If not, judge whether a continuous subsequence (length 3) can be formed starting with the current element. If yes, eliminate the continuous subsequence
• Otherwise, false is returned

const isPossible = function(nums) {
    let max = nums[nums.length - 1]
    // arr: stores the number of occurrences of each number in the original array
    // tail: stores the number of consecutive subsequences ending in num and conforming to the meaning of the question
    let arr = new Array(max + 2).fill(0), 
        tail = new Array(max + 2).fill(0)
    for(let num of nums) {
        arr[num] ++
    }
    for(let num of nums) {
        if(arr[num] === 0) continue
        else if(tail[num-1] > 0){
            tail[num-1]--
            tail[num]++
        }else if(arr[num+1] > 0 && arr[num+2] > 0){
            arr[num+1]--
            arr[num+2]--
            tail[num+2]++
        } else {
            return false
        }
        arr[num]--
    }
    return true
}

Complexity analysis:

• Time complexity: O(n)
• Space complexity: O(n)

More answers

7.11 Full Permutation Problem

Given a sequence of {no repeated} numbers, all possible permutations are returned.

Example:

input: [1,2,3]
output:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

Solution: backtracking algorithm

This problem is a classic application scenario of backtracking algorithm

1. Algorithm strategy

Backtracking algorithm is a search method, heuristic method. It will make a choice at each step. Once it is found that the choice cannot get the expected result, it will backtrack and make a choice again. Depth first search uses the idea of backtracking algorithm.

2. Applicable scenarios

The backtracking algorithm is very simple. It just keeps trying until it gets the solution. Its algorithmic idea makes it usually used to solve the breadth search problem, that is, select a solution that meets the requirements from a set of possible solutions.

3. Code implementation

We can write that the full arrangement of array [1, 2, 3] is:

• First write the full permutation starting with 1, which are: [1, 2, 3], [1, 3, 2], that is, the full permutation of 1 + [2, 3];
• Then write the full permutation starting with 2, which are: [2, 1, 3], [2, 3, 1], that is, the full permutation of 2 + [1, 3];
• Finally, write the full permutation starting with 3. They are: [3, 1, 2], [3, 2, 1], that is, the full permutation of 3 + [1, 2].

That is, the processing idea of backtracking is a bit similar to enumeration search. We enumerate all the solutions and find the solution that meets the expectation. In order to enumerate all possible solutions regularly and avoid omission and repetition, we divide the problem solving process into multiple stages. At each stage, we will face a fork in the road. We will choose a road at will. When we find that this road can't go (it doesn't meet the expected solution), we will go back to the previous fork in the road and choose another way to continue.

This is obviously a {recursive structure;

• The termination condition of recursion is: enough numbers in a permutation have been selected, so we need a variable to indicate the layer to which the current program recurses. We call this variable ， depth, or ， index, to indicate that what we want to determine is the number marked ， index ， in a full permutation;
• Used (object): used to indicate whether a number is selected. If the number (num) is selected, this is set to "used[num] = true", so that when considering the next position, it can judge whether the number has been selected with the time complexity of O(1). This is an idea of "space for time".

let permute = function(nums) {
    //Use an array to hold all possible permutations
    let res = []
    if (nums.length === 0) {
        return res
    }
    let used = {}, path = []
    dfs(nums, nums.length, 0, path, used, res)
    return res
}
let dfs = function(nums, len, depth, path, used, res) {
    //All the numbers have been filled in
    if (depth === len) {
        res.push([...path])
        return
    }
    for (let i = 0; i < len; i++) {
        if (!used[i]) {
            //Dynamic maintenance array
            path.push(nums[i])
            used[i] = true
            //Continue to fill in the next number recursively
            dfs(nums, len, depth + 1, path, used, res)
            //Undo operation
            used[i] = false
            path.pop()
        }
      
    }
}

4. Complexity analysis

• Time complexity: O(n * n!), Where n is the length of the sequence, which is a permutation. The number of permutations per layer is: A ^ m ^ ~ n ~ = n/ (n−m)! ， Therefore, all permutations are: A^1^ ~n~ + A^2^ ~n ~ +... + A ^ n-1 ^ ~ n ~ = n/ (n−1)! + n!/(n−2)! + … + n! = n! * (1/(n−1)! + 1/(n−2)! + … + 1) <= n! * (1 + 1/2 + 1/4 + … + 1/2^n-1^) < 2 * n! And each internal node circulates n times, so the time complexity of non leaf nodes is O(n * n!)
• Space complexity: O(n)

More answers

7.12 bracket generation

The number n represents the logarithm of the generated parentheses. Please design a function to generate all possible and effective combinations of parentheses.

Example:

Input: n = 3
 Output:[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]

Answer: backtracking algorithm (depth first traversal)

Algorithm strategy: backtracking algorithm is a search method and heuristic method. It will make a choice at each step. Once it is found that the choice cannot get the expected result, it will backtrack and make a choice again. Depth first search uses the idea of backtracking algorithm.

Corresponding to this question, we can add (or) each time. Note:

• The condition for joining (yes) is whether there is (optional) at present
• When joining), it is restricted by (if the selected result is less than or equal to the selected result, it cannot be selected at this time), for example, if it is (), continue to select) is (), which is illegal

Code implementation:

const generateParenthesis = (n) => {
    const res = []
    const dfs = (path, left, right) => {
        //It must be illegal. It ends early
        if (left > n || left < right) return
        //End condition reached
        if (left + right === 2 * n) {
            res.push(path)
            return
        }
        //Choose
        dfs(path + '(', left + 1, right)
        dfs(path + ')', left, right + 1)
    }
    dfs('', 0, 0)
    return res
}

Complexity analysis (source: leetcode official solution):