[experimental principle]

1. Eight digital problems
Judging whether there is a solution or not: directly judge whether there is a solution according to the reverse order number. For an eight digit number, after the sequence is arranged, each time the empty bit and the adjacent bit are exchanged. After research, it will be found that each exchange, the increase of the reverse order number is even, that is, it does not change the parity, so the parity of the reverse order number in the initial and target states is the same.

2. State chart search
(1) Search tree: the nodes and edges in the search process form a tree type digraph according to the connection relationship of the original graph, which is called search tree.
(2) Search method: tree search - record all nodes and edges in the search process
(3) Path acquisition: tree search reverse solution
(4) CLOSED table and OPEN table: CLOSED table stores a growing search tree for tree search, and a growing broken line for line search, which is the desired path. The OPEN table stores the current nodes to be examined.

3. A algorithm
(1) Heuristic function: a function used to estimate the proximity of node X to the target node Sg on the search tree. It is recorded as h(x)
(2) Evaluation function: f(x)=g(x)+h(x)f(x)=g(x)+h(x)f(x)=g(x)+h(x); where g(x)g(x)g(x) is the cost function and h(x)h(x)h(x) H (x) is the heuristic function. Or defined as: F (x) = D (x) + H (x) f (x) = D (x) + H (x) f (x) = D (x) + H (x); D (x) d (x) d (x) is the depth of xxx

(3) Algorithm steps
Step1Step1Step1: add S0 to the OPEN table
Step2Step2Step2: if the OPEN table is empty, the search fails and exits
Step3Step3Step3: move the first node N from the OPEN table to the CLOSED table
Step4Step4Step4: if N is the target node, the search is successful
Step5Step5Step5: if it is not extensible, turn to Step2Step2Step2
Step6Step6Step6: handle the extended word nodes accordingly:
① Generate whether there are existing points in the OPEN table or CLOSED table in the child node; if there are any, then consider whether there are predecessor nodes of N, and delete them; if there are other nodes, delete them, and modify their f(x) value;
② Modify the pointer of the parent node, add the remaining child nodes to OPEN, sort the OPEN table, and turn to Step2Step2Step2

[experiment content]

1. requirements

(1) The cost function G(x)G(x)G(x) and heuristic function H(X)H(X)H(X) H (x) are defined and solved by algorithm A.
(2) Enter the initial and target states.
(3) Outputs the route from the initial state to the target state.

2. Code list

#include <iostream>
#include <type_traits>
#include<stdlib.h>
#include <windows.h>
#include <time.h>
using namespace std;
#define MAXNUM 100
#define OK 1
#define ERROR 0
int ss0[9] = { 0 };  // Initial node, to be input
int ssg[9] = { 0 };  // Target node, to be input
class Table; 

class Node
{  // Node class
public:
	Node();  // Default constructor 
	Node(int s[]);  // Constructor initialized with array
	Node &operator=(const Node ss); //Operator overload for assignment
	void showStatus();	// Display node status
	bool operator==(Node &N); // Operator overload, used to determine whether it is equal
	int Ancestors(Node ss);			// Ancestor node
	int gx();		// Cost function
	int hx();		// Heuristic function
	int fx();		// Valuation function
	int expand( Node kid[]);	// Expand child nodes
	friend class Table;				// Friend class Table
	friend int A(Node S0, Node Sg);   // Algorithm of friend function A

private:
	int *status = new int[9]; // node state
	int steps;  // Node depth
	int f;		// Node fx value ֵ
	Node *father; // ָ parent node pointer
};
Node deleted;	// Represents the deleted node for comparison and assignment
Node::Node()	// Default constructor 
{ 
	for (int i = 0; i < 9; i++) {
		status[i] = 0;
	}
	f = steps = 0;
	father = NULL;
}
Node::Node(int s[])// Constructor initialized with array
{ 
	for (int i = 0; i < 9; i++) {
		status[i] = s[i];
	}
	steps = 0;
	f = fx();
	father = NULL;
}
Node& Node::operator=(const Node ss)//Operator overload for assignment
{ 
	for (int i = 0; i < 9; i++) {
		status[i] = ss.status[i];
	}
	steps = ss.steps;
	f = ss.f;
	father = ss.father;
	return *this;
}
void Node::showStatus()// Display node status
{ 
	cout << "┏━━━━━━━━━━┓" << endl;
	for (int i = 0; i < 3; i++) { 
		cout << "┃";
		for (int j = 0; j < 3; j++) { 
			if (status[i * 3 + j] == 0) {
				cout << "   ";
			}
			else {
				cout << "  " << status[i * 3 + j];
			}
		}
		cout << " ┃" << endl;
	}
	cout << "┗━━━━━━━━━━┛" << endl;
}
bool Node::operator==(Node &N)
{ 
	for (int i = 0; i < 9; i++) { 
		if (status[i] != N.status[i]) {
			return false;
		}
	}
	return true;
}
int Node::Ancestors(Node ss)	// If ss is the ancestor node, if yes, it will return a high number of generations
{ 
	int generation = 1; 
	Node *p = father;
	while (p != NULL) {
		if (*p == ss) {
			return generation;
		}
		p = p->father;
		generation++;
	}
	return 0;
}
int Node::gx()
{
	return steps;// Cost function value is node depth
}
int Node::hx()
{ 
	int h = 0;
	for (int i = 0; i < 9; i++) {
		if (status[i] != ssg[i]) {
			h++;	// If each bit is inconsistent with the target node, the heuristic function value is increased by one
		}
	}
	return h;
}
int Node::fx()
{
	return (gx() + hx());
}
int Node::expand(Node kid[])
{
	int point, i, j;
	for (i = 0; i < 9; i++) {
		if (status[i] == 0) {
			point = i;
		}
	}
	i = 0;
	if (point - 3 >= 0) { // Prevent upward expansion across borders
		for (j = 0; j < 9; j++) {
			kid[i].status[j] = status[j];
		}
		swap(kid[i].status[point], kid[i].status[point - 3]);
		kid[i].steps = steps + 1;
		kid[i].f = kid[i].fx();
		i++;
	}
	if (point + 3 <= 8) { // Prevent downward expansion out of bounds
		for (j = 0; j < 9; j++) {
			kid[i].status[j] = status[j];
		}
		swap(kid[i].status[point], kid[i].status[point + 3]);
		kid[i].steps = steps + 1;
		kid[i].f = kid[i].fx();
		i++;
	}
	if (point % 3 != 0) { // Prevent left extend out of bounds
		for (j = 0; j < 9; j++) {
			kid[i].status[j] = status[j];
		}
		swap(kid[i].status[point], kid[i].status[point - 1]);
		kid[i].steps = steps + 1;
		kid[i].f = kid[i].fx();
		i++;
	}
	if ((point + 1) % 3 != 0) { // Prevent right expansion out of bounds
		for (j = 0; j < 9; j++) {
			kid[i].status[j] = status[j];
		}
		swap(kid[i].status[point], kid[i].status[point + 1]);
		kid[i].steps = steps + 1;
		kid[i].f = kid[i].fx();
		i++;
	}
	if (i == 0) {
		return ERROR;
	}
	else {
		return i; 
	}
}

class Table
{ 
public:
	Table();  // Constructor
	int Add(Node S);   // Add node to table
	int Delete(int i);     // Delete node
	bool isEmpty();      // Judgement of surface space
	int Search(Node NS);    // Find NS node in table
	int Sort();				// Sort tables in fx ascending order
	void showNode();	// Print table
	friend int A(Node S0, Node Sg); // A algorithm

private:
	Node node[MAXNUM];  // Node in table
	int length;   // Table length
};
Table::Table()
{// Constructor
	for (int i = 0; i < MAXNUM; i++) { // Initialization table length is 0
		length = 0;
	}
}
int Table::Add(Node S)
{
	if (length < MAXNUM) { // Determine if it is full
		node[length] = S;
		length++;
		return OK;
	}
	else {
		return ERROR;
	}
}
int Table::Delete(int i)
{ 
	if (i > 0 && i < length) {  // Judge whether the table is empty
		for (int j = i - 1; j < length - 1; j++) {
			node[j] = node[j + 1];
		}
		length--;
		return OK;
	}
	else if (i == length)
	{
		node[i - 1]=deleted;
		length--;
		return OK;
	}
	else {	// Error prompt
		cout << "Input illegal in delete function!" << endl;
		return ERROR;
	}
}
bool Table::isEmpty()
{
	if (length > 0) { // Not empty
		return false;
	}
	else {// Empty
		return true;
	}
}
int Table::Search(Node NS)
{
	for (int i = 0; i < length; i++) {
		if (NS == node[i]) {
			return i + 1; // Return the sequence number of NS in the table
		}
	}
	return 0;
}
int Table::Sort()
{ // Sort in fx ascending order
	if (isEmpty()) {
		return ERROR;
	}
	else {
		Node temp;
		for (int i = 0; i < length - 1; i++) {
			for (int j = 0; j < length - 1 - i; j++) {
				if (node[j].f > node[j + 1].f) {
					temp = node[j];
					node[j]=node[j + 1];
					node[j + 1] = temp;
				}
			}
		}
		return OK;
	}
}
void Table::showNode()
{ // Print table
	if (length == 0) {
		cout << "Empty!" << endl;
	}
	else {
		for (int i = 0; i < length - 1; i++)
		{
			node[i].showStatus();
			cout << "     ↓     " << endl;
		}
		node[length - 1].showStatus();
	}
}
Table Path; // Record solution path

int inversions(int S[])	// Calculating the reverse number of s array
{
	int i = 0, point;
	int ss[8] = { 0 };
	int s_inversions = 0;	//Inverse number
	for (i = 0; i < 9; i++) {
		if (S[i]==0){
			point = S[i];
		}
		else {
			ss[i] = S[i];
		}
	}
	for (i = point; i < 9; i++) {
		ss[point] = S[point + 1];
	}
	for (i = 0; i < 8; i++) {
		for (int j = i; j < 8; j++)
		{
			if (ss[i] > ss[j])
			s_inversions++;
		}
	}
	return s_inversions;
}
int A(Node S0, Node Sg)
{	// A algorithm
	if ((inversions(S0.status) + inversions(Sg.status)) % 2 != 0) {
		return ERROR;
	}
	Table OPEN, CLOSED;		// OPEN and CLOSED tables
	int &m = OPEN.length;		// OPEN table long alias
	int &n = CLOSED.length;	// CLOSED table long alias
	int time = 0;						
	Node *kid = new Node[4];
	
	cout << "Original status: " << endl; 
	S0.showStatus();
	cout << "Goal status: " << endl;
	Sg.showStatus();
	cout << endl << "========================" << endl;
	OPEN.Add(S0);					//  Step 1: add S0 to the OPEN table
	while (true) {
		if (OPEN.isEmpty()) {		// Step 2: if the OPEN table is empty, the search fails and exits
			return ERROR;
		}
		CLOSED.Add(OPEN.node[0]);	// Step 3: move the first node N from the OPEN table to the CLOSED table
		Node &N = CLOSED.node[n - 1];	// 
		OPEN.Delete(1);

		if (N==Sg) {		// Step4: if N is the target node, the search is successful
			cout << "Find succeed!" << endl;
			cout <<  "========================" << endl;
			system("pause");
			return OK;
		}
		int kid_num = N.expand(kid);
		int flag = 4;
		for (int i = 0; i < kid_num; i++) {
			if ((OPEN.Search(kid[i]) != 0) || (CLOSED.Search(kid[i]) != 0))
			{
				flag--;	
			}
		}
		if (flag == ERROR) { // Step5: if it is not extensible, turn to Step2
			continue;
		}
		for (int i = 0; i < kid_num; i++) { //Step 6: handle the extended word nodes accordingly
			int exOPEN = OPEN.Search(kid[i]);// Generate whether there are existing points in the OPEN table in the child node
			int exCLOSED = CLOSED.Search(kid[i]);// Generate whether there are existing points in the CLOSED table in the child node
			if (exOPEN > 0) {  
				if (N.Ancestors(kid[i])) {// If there is, then consider whether there is a predecessor node of N, and delete if there is
					kid[i] = deleted;
				}
				else {  // For other nodes, delete them, and modify their f(x) values
					if (OPEN.node[exOPEN - 1].f > kid[i].f) {
						OPEN.node[exOPEN - 1].father = &N;
						OPEN.node[exOPEN - 1].f = kid[i].f;
					}
					kid[i] = deleted;
				}
			}	// if exOPEN>0
			else if (exCLOSED>0) {
				if (N.Ancestors(kid[i])!=0) {// If there is, then consider whether there is a predecessor node of N, and delete if there is
					kid[i] = deleted;
				}
				else {  // For other nodes, delete them, and modify their f(x) values
					if (CLOSED.node[exCLOSED - 1].f > kid[i].f) {
						CLOSED.node[exCLOSED - 1].father = &N;
						CLOSED.node[exCLOSED - 1].f = kid[i].f;
					}
					kid[i] = deleted;
				}
			}	// else if
			else {
				kid[i].father = &N; // Modify parent node pointer
			}
			if (!(kid[i] == deleted))
			{
				OPEN.Add(kid[i]);	// The remaining child nodes are added to OPEN
			}
		}
		OPEN.Sort();  //OPEN table sort
		if ((Path.node[Path.length - 1] == *OPEN.node[0].father)&&!OPEN.isEmpty()) {
			Path.Add(OPEN.node[0]);
		}
		cout << "==========open============" << endl;
		OPEN.showNode();
		cout << endl;
		cout << "==========closed==========" << endl;
		CLOSED.showNode();
		cout << endl;
		cout << "==========path============" << endl;
		Path.showNode();
		cout << endl;
		system("pause");
		system("cls");
	}// while
	delete kid;
	return ERROR;
}

int main()
{
	cout << "Input the original status: ";	// Input initial state
	for (int i = 0; i < 9; i++) {
		cin >> ss0[i];
	}
	Node S0(ss0);
	Path.Add(S0);
	cout << "Input the goal status:     ";// Enter target status
	for (int i = 0; i < 9; i++) {
		cin >> ssg[i];
	}
	Node Sg(ssg);
	cout << endl;
	if (A(S0, Sg) == OK) {	//Search success
		cout << endl << endl;
		cout << "The find process is: " << endl;
		Path.showNode();// Print solution path
	}
	else {	// Prompt search failed
		cout << "Search failed! This status have no solution!" << endl;
	}
	system("pause");
	return 0;
}

3. Operation results

(1) Manual entry of initial and target states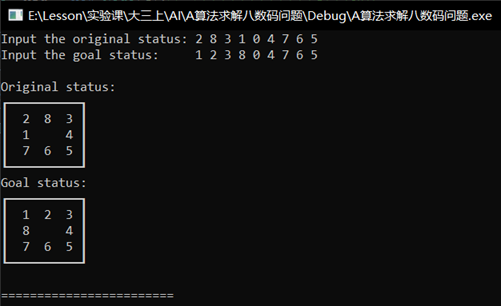

(2) Show OPEN and CLOSED tables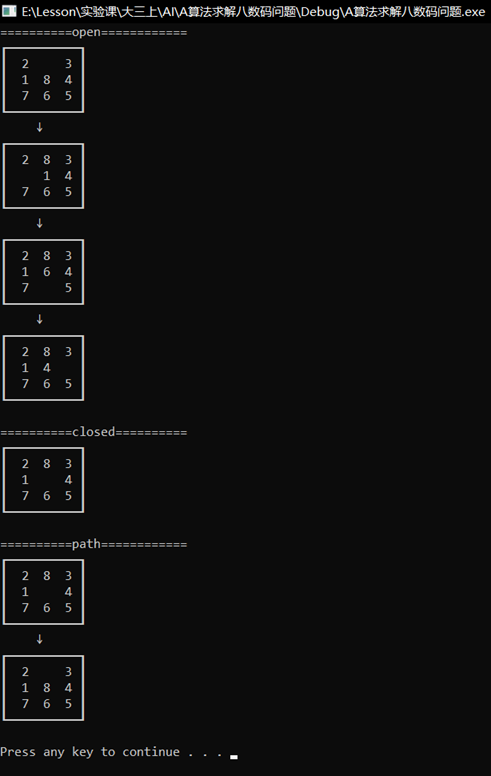

(3) Press enter to refresh the interface, the second sub node expansion: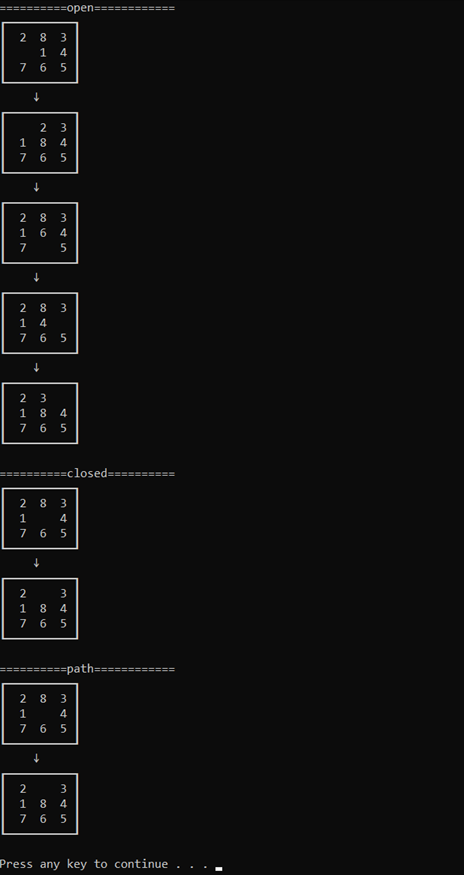

(4) Search succeeded, print search path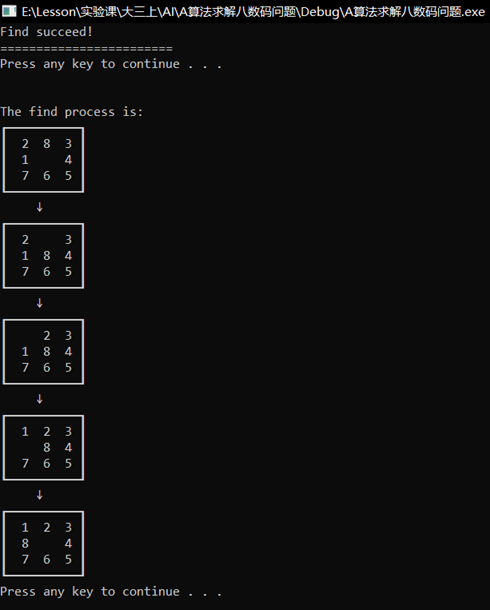

[summary or discussion]

In this experiment, I directly followed the textbook (Introduction to artificial intelligence technology (Third Edition) during the 11th Five Year Plan
Mr. Lian / November 2018/ In step 6, judge whether there are existing points in the OPEN table or CLOSED table in the generated sub node; if there are, consider whether there are N predecessor nodes in the generated sub node; if there are, delete them; if there are other nodes, modify their f(x) value. Here, I delete the generated sub node 2 and modify the CLOSED table There are no duplicate nodes in table D, but these nodes are not added to the OPEN table for re expansion, resulting in a life and death cycle in the case of many steps. In addition, it is discussed with a student that setting a clever heuristic function can improve the search efficiency, which can still be modified here.