Tip: after the article is written, the directory can be generated automatically. Please refer to the help document on the right for how to generate it

preface

I started to read CS224n when preparing for the retest, which is a well-known course in natural language processing. When I first started learning word vectors, I was confused. The more I read the online articles, the more confused I became. So I wrote this article, hoping to help the students to better understand word vectors

1, What is a word vector?

Computer is an iron knot. It doesn't know how to read language. Therefore, if it wants to understand natural language symbols, it must digitize language symbols. Then the means of digitization is word vector - each language symbol is represented by a vector.

1.1 one hot representation

Some students who are based on machine learning first think that all symbols are regarded as a space. If a symbol appears, the position of the symbol is marked as 1, and if it does not appear, it is marked as 0.
For example, there is a dictionary that contains only 8 words, I, pet, thing, yes, one, strip and dog. (orderly)
Then the vector representation of these words can be:
Me: [1,0,0,0,0,0,0,0,0]
[0,1,0,0,0,0,0,0,0]
Favorite: [0,0,1,0,0,0,0,0]
Object: [0,0,0,1,0,0,0,0]
Yes: [0,0,0,0,1,0,0,0,0]
1: [0,0,0,0,1,0,0]
Article: [0,0,0,0,0,0,1,0]
Dog: [0,0,0,0,0,0,0,1]
This representation method is called one hot representation, which is also called discrete representation. Its advantages are: easy to understand and good robustness. But its disadvantages are also obvious: imagine that if there are 100000 words and each vector is a vector of 100000 dimensions, the vector space will explode. At the same time, because of the knowledge of linear algebra, we can know that any two vectors are orthogonal, so we can't express the relationship between words.

1.2 distribution representation

word embedding is a method of transforming words into a distributed representation. Distributed representation represents a word as a continuous dense vector of fixed length. Its advantages are: there is a similar relationship between words (non orthogonal) and each dimension has its specific meaning.

2, Co occurrence matrix generates word vector

2.1 co occurrence matrix

By counting the common occurrence times of words in a window with a specified size in advance, the words are divided into two kinds, the center word and other words. Move forward only one word at a time. Now there are two sentences
START All that glitters isn't gold END
START All''s well that ends well END
The dictionary is: All,All's, end, start, ends, glitters, gold, isn; t. That, well
Assuming that the window is 1, the co-occurrence matrix is:

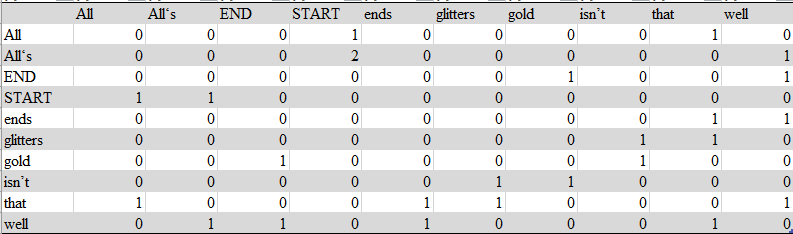
For the first sentence, the status of the start window is [START,All]. At this time, the central word is start. Therefore, start and All co-exist. In the matrix, start is the row and All is the position of the column plus 1. Then move the window backward by one word. At this time, the status is [START,All,that], and the central word is All. Therefore, add 1 where the behavior All is listed as start and that. Repeat the operation until the end of the sentence. After the first sentence is processed, the second sentence is processed to obtain the above matrix.
Suppose the window is 2, the initial state is [START,All,that], and the central word is START. Therefore, add 1 to the position where the behavior START is listed as All and that is listed as that. Subsequent operations are similar to window 1.
Each column (or row) of the co-occurrence matrix can be regarded as a word vector.
The code for realizing co-occurrence matrix is as follows (example):

def compute_co_occurrence_matrix(corpus, window_size=4):

    words, num_words = distinct_words(corpus)
    M = None
    word2Ind = {}
    for (id,key) in enumerate(words):
        word2Ind[key]=id
    M=np.zeros((len(words),len(words)))

    for sentence in corpus:
        for i in range(len(sentence)):
            window = list(range(max(0, i - window_size), min(i + window_size + 1, len(sentence))))
            window.remove(i)
            for j in window:
                M[word2Ind[sentence[i]], [word2Ind[sentence[j]]]] += 1
                M[word2Ind[sentence[j]], [word2Ind[sentence[i]]]] += 1
    M=M/2
    return M, word2Ind
    
def distinct_words(corpus):
	#Remove duplicate words from the corpus
    corpus_words = []
    num_corpus_words = -1
    for scentence in corpus:
        for word in scentence:
            if word not in corpus_words:
                corpus_words.append(word)
    num_corpus_words = len(corpus_words)
    corpus_words = sorted(corpus_words)
    return corpus_words, num_corpus_words

2.2 singular value decomposition (SVD)

We can see that the above matrix is still a 10 * 10 matrix, and its word vector is still 10 dimensions, which is the same as the length of the dictionary. Therefore, SVD is used to reduce the dimension of the word vector. If you are interested in SVD, you can look at the mathematical principle, mainly adjusting the library.
SVD dimensionality reduction code is as follows (example):

def reduce_to_k_dim(M, k=2):
    n_iters = 10  # Use this parameter in your call to `TruncatedSVD`
    M_reduced = None
    print("Running Truncated SVD over %i words..." % (M.shape[0]))
    svd = TruncatedSVD(n_components=k, n_iter=n_iters, random_state=42)
    M_reduced=svd.fit_transform(M, y=None)
    print("Done.")
    return M_reduced

The above code converts the word vector into a k-dimensional vector.

3, Summary

For example, the above is what we are going to talk about today. This paper only briefly introduces the concept of word vector and the method of co-occurrence matrix to represent word vector. Because there are many contents of word vector, we plan to write word2vec in the next blog. Interested partners can pay attention to it.