subject

Five athletes participated in the 10m platform diving competition. They were asked to predict the result of the competition:
Player A said: B second, I third;
Player B said: I'm second, E is fourth;
Contestant C said: I am the first and D is the second;
Player D said: C finally, I'm third;
Player E said: I'm fourth, A is first;
After the competition, each contestant is half right. Please program to determine the ranking of the competition.

thinking

1. Let the number 12345 represent the rank 12345, create an array a[5], store the ABCDE rank from a[0] to a[4], and store 12345 in the array in a certain order. The final result of the array is their rank, for example, 12345 is a = 1, B = 2, C = 3, d = 4, e = 5
2. Give the full arrangement of 12345 in the array.
3. Set the screening conditions according to the meaning of the question. The qualified arrangement is the result.
One of the core problems is how to use code to traverse the full arrangement, and the other is how to translate the question stem into judgment conditions

Achieve full permutation

The idea of recursion can be used to turn the total arrangement of N numbers into the total arrangement of n-1 numbers after they are fixed respectively
(the circular method is also acceptable, but the code quantity is huge and the modifiability is poor. Here we focus on the recursive method)

For example, in this question, we want to achieve 12345 full permutation
Step 1: fix 1 and find the full arrangement of the remaining numbers
Step 2: fix 2 and find the full arrangement of the remaining numbers
...
Step 5: fix 5 and find the full arrangement of the remaining numbers

Then, each step to find the full arrangement of the remaining numbers adopts the method of fixing a single element first and then finding the sub arrangement, and finally it can be solved.

When implementing the program, we should pay attention to that the logic is slightly different from the above

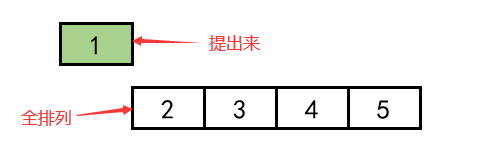
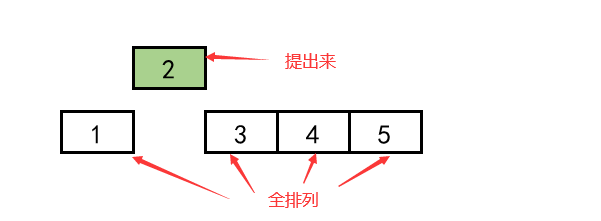
Because we use an array instead of a linked list to store data (that is, we can't suddenly empty the middle of the elements), we can't directly realize "fix 2 and find the full arrangement of 1345", so we first exchange the position between 2 and the first element of the array, and let the remaining arrays form an array to continue to realize the full arrangement; Similarly, when 3 is proposed, it is also to exchange positions between 3 and the first element of the array to construct a subarray; 4. 5 similarly

For the step of fixing 2 to find the full arrangement of 1345, after finding the full arrangement of 1345, the order of 2 and the first element should be exchanged back, otherwise the original array order will change. It can be understood that the step of bold font in the previous paragraph is an auxiliary step added by ourselves, just as you will draw an auxiliary line when drawing the median line with a ruler and gauge. Finally, you need to erase the auxiliary line. The way to "erase" the trace of program execution is to execute the program against it. In this problem, you exchange 2 and the first element back.

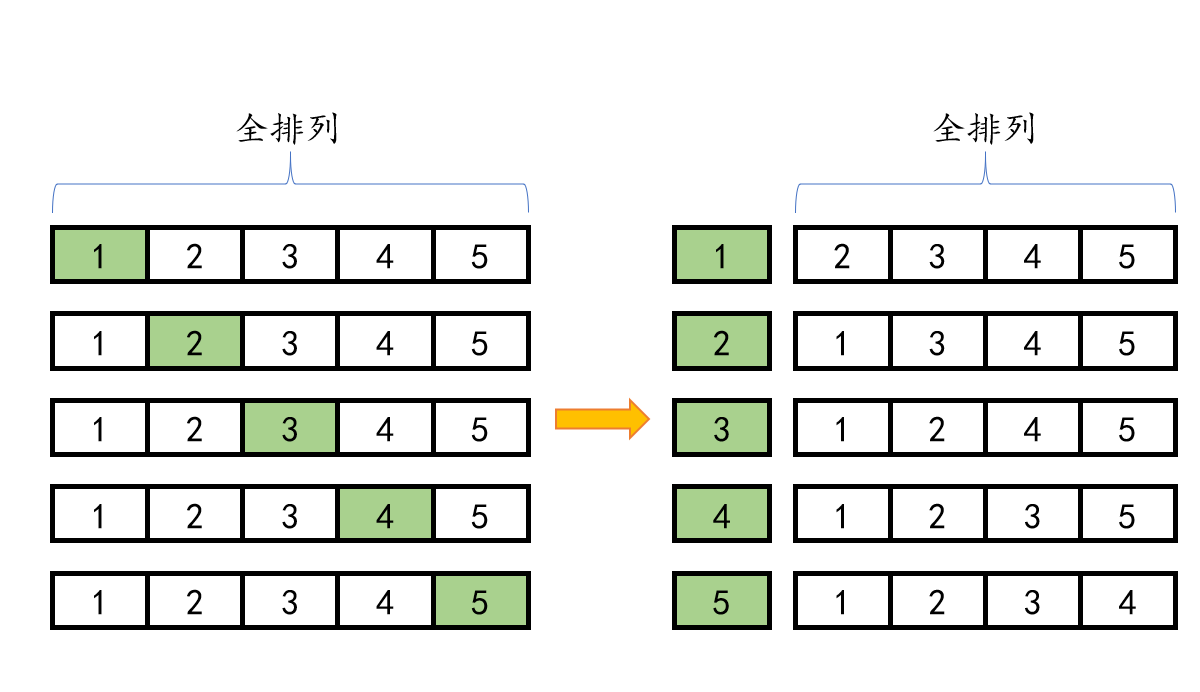
The first step is to find the total permutation of 2345
The full arrangement of 2345 can also be split in this way:
Step 1: split 2 to find the full arrangement of the remaining numbers
Step 2: split 3 to find the full arrangement of the remaining numbers
Step 3: split 4 to find the full arrangement of the remaining numbers
Step 4: split 5 to find the full arrangement of the remaining numbers

The first step above becomes to find the total permutation of 345
The full arrangement of 345 can be split as follows:
Step 1: split 3 to find the full arrangement of the remaining numbers
Step 2: split 4 to find the full arrangement of the remaining numbers
Step 3: split 5 to find the full arrangement of the remaining numbers

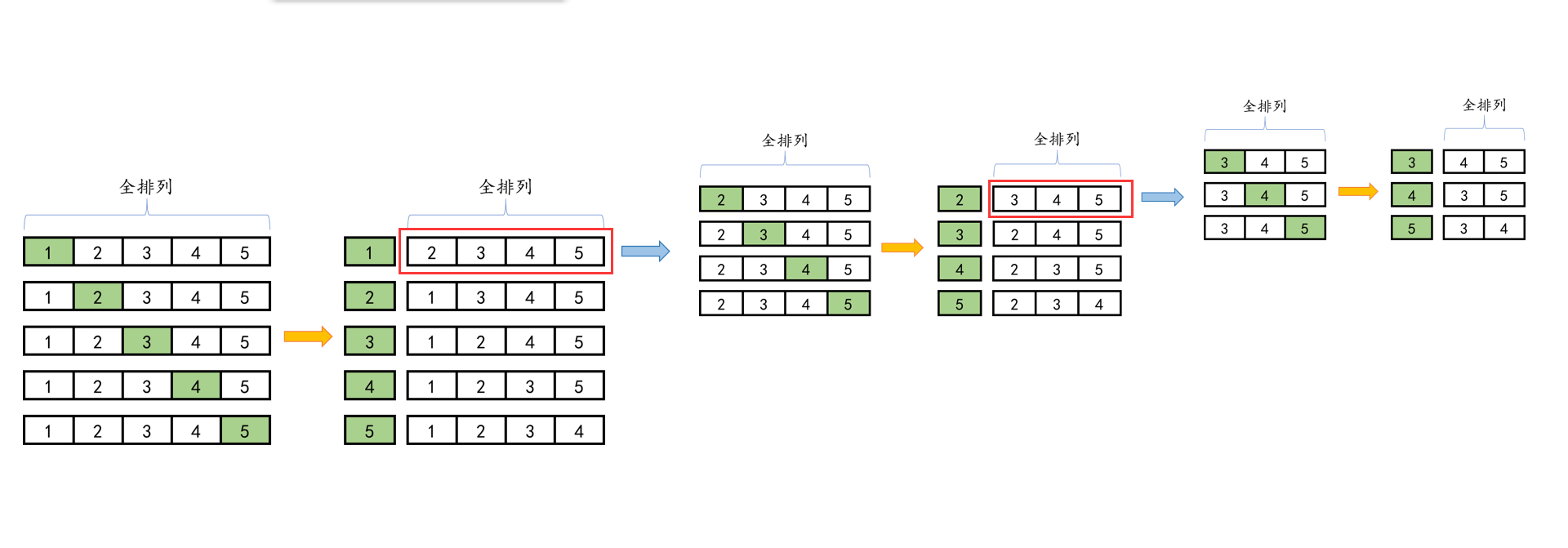
By analogy, we can get the full arrangement of all numbers

So the steps of recursive function are:
1. Exchange a number with the first element
2. Realize the full arrangement of the remaining numbers (call recursive functions)
3. Exchange this number with the first element
Write as function:
(the exchange function is the content exchange function, and the perm function is the function of seeking complete permutation. It is suggested to understand it in combination with the complete code at the end of the text)

exchange(&str[j], &str[start]);//Put each element first in turn
perm(str, start + 1, str_size);//Arrange the remaining elements
exchange(&str[j], &str[start]);//Then restore the first element back to restore the array order

Set judgment conditions

Let's take a look at the judgment conditions of the topic:
"Player A said: B second, I third;
Player B said: I'm second, E is fourth;
Contestant C said: I am the first and D is the second;
Player D said: C finally, I'm third;
Player E said: I'm fourth, A is first;
At the end of the game, each player was half right. "

Because only half of every sentence is right, that is to say, the first half of the sentence may be true, the second half of the sentence may be false, or the first half of the sentence may be false, and the second half of the sentence may be true
So A's words can be interpreted as: (B is second and I'm not third) or (B is not second and I'm third)
B's words can be interpreted as: (I'm second and E is not fourth) or (I'm not second and E is fourth)
Similarly, CDE can be interpreted

Written as if judgment:

if (((str[1] == 2 && str[0] != 3) || (str[1] != 2 && str[0] == 3))
 && ((str[1] == 2 && str[4] != 4) || (str[1] != 2 && str[4] == 4))
 && ((str[2] == 1 && str[3] != 2) || (str[2] != 1 && str[3] == 2))
 && ((str[2] == 5 && str[3] != 3) || (str[2] != 5 && str[3] == 3))
 && ((str[4] == 4 && str[0] != 1) || (str[4] != 4 && str[0] == 1)))

code

(the C code involves some knowledge of pointer arrays. If you have difficulties, it is recommended to lay the foundation first and then look at it.)
It is strongly recommended to look back at the previous method against the code

#include <stdio.h>

void exchange(int* a, int* b)//The exchange function exchanges the values of two variables
{
    int c = *a;
    *a = *b;
    *b = c;
}

void perm(int str[], int start, int str_size)//STR pass in the object of Full Permutation start the starting point of Full Permutation str_size is the number of elements
{
    int i = 0, j = 0;

    if (start == str_size)//start == str_size means start = STR in the previous round_ Size - 1, that is, when the traversal ends, it jumps out of recursion
    {
        /* Output the current arrangement */
        if (((str[1] == 2 && str[0] != 3) || (str[1] != 2 && str[0] == 3))
            && ((str[1] == 2 && str[4] != 4) || (str[1] != 2 && str[4] == 4))
            && ((str[2] == 1 && str[3] != 2) || (str[2] != 1 && str[3] == 2))
            && ((str[2] == 5 && str[3] != 3) || (str[2] != 5 && str[3] == 3))
            && ((str[4] == 4 && str[0] != 1) || (str[4] != 4 && str[0] == 1)))
        printf("A=%d B=%d C=%d D=%d E=%d\n", str[0], str[1], str[2], str[3], str[4]);
    }
    else
    {
        for (j = start; j < str_size; j++)
        {
            exchange(&str[j], &str[start]);//Put each element first in turn
            perm(str, start + 1, str_size);//Arrange the remaining elements
            exchange(&str[j], &str[start]);//Then restore the first element back to restore the array order
        }
    }
    return;
}
int main()
{
    int a[5] = { 1,2,3,4,5 };
    perm(a, 0, 5);
    return 0;
}

Operation screenshot:

So the final ranking is 12345 = BDAEC

summary

Problem solving Trilogy:
1. Traverse all permutations
2. Set the screening conditions according to the meaning of the question
3. Output the arrangement according to the meaning of the question

ps: the idea of this article can solve a number of Full Permutation problems. I hope my partners can understand the principle and draw inferences from one instance