A * preliminary detailed explanation of algorithm

Please see Baidu Encyclopedia for details
The core valuation function: f(x) = g(x) + h(x)

• g(x) is the distance function from the starting point, such as how many steps have been taken from the starting point.
• h(x) is the heuristic search function for the current position to reach the end point. Change according to the meaning of the question.

General form of h(x)

1, When finding the shortest path problem:

1. Manhattan distance (when only four directions are allowed):
   

The function for calculating Manhattan distance is as follows. D here refers to the movement cost between two adjacent nodes, which is usually a fixed constant.

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy)

1. Diagonal distance (when eight directions are allowed)
   

The function for calculating the diagonal distance is as follows. D2 here refers to the moving cost between two adjacent nodes obliquely. If all nodes are square, the value is sqrt(D)

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

1. Euclidean distance (when any direction is allowed)

Linear distance between two points:

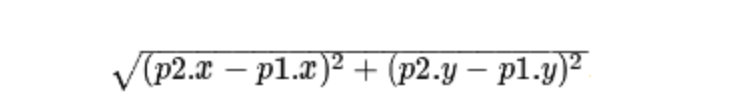
2, When solving the shortest path variant problem

In fact, there are many problems that are not very strict shortest path problems. In this case, A * algorithm can also be used according to the situation, such as moving distance problem.

Given the minimum number of operations required to move a pattern to the answer, h(x) can be represented by the different degree of the two graphs.

Using f(x) to complete A * algorithm

The necessary data structure of A * algorithm is A minimum heap. We also need to customize A node structure, which overloads the sorting method of the minimum heap. The sorting method must be carried out according to the size returned by the evaluation function f.
Of course, similar to bfs, weight removal is generally required.

Not much to say, let's complete the following problem with A * algorithm according to these steps!

Examples

OJ platform

Problem solving code

#include <algorithm>
#include <cstdio>
#include <queue>
#include <set>
using namespace std;
const int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
int fx, fy;
char ch;
struct matrix {//Custom matrix type, overload < for set judgment
    int a[5][5];
    bool operator<(const matrix& x) const {
        for (int i = 1; i <= 3; i++)
            for (int j = 1; j <= 3; j++)
                if (a[i][j] != x.a[i][j]) return a[i][j] < x.a[i][j];
        return false;
    }
} f, st;
int h(matrix a) {//h(x) function
    int ret = 0;
    for (int i = 1; i <= 3; i++)
        for (int j = 1; j <= 3; j++)
            if (a.a[i][j] != st.a[i][j]) ret++;
    return ret;
}
struct node { //node structure, record the steps taken and the corresponding graph, and use the estimation function to build the minimum heap
    matrix a;
    int t;
    bool operator<(const node& x) const { return t + h(a) > x.t + h(x.a); }
} x;
priority_queue<node> q;  //Search queue
set<matrix> s;           //Prevent duplicate search queues
int main() {
    st.a[1][1] = 1;  //Definition standard table
    st.a[1][2] = 2;
    st.a[1][3] = 3;
    st.a[2][1] = 8;
    st.a[2][2] = 0;
    st.a[2][3] = 4;
    st.a[3][1] = 7;
    st.a[3][2] = 6;
    st.a[3][3] = 5;
    for (int i = 1; i <= 3; i++)  //input
        for (int j = 1; j <= 3; j++) {
            scanf(" %c", &ch);
            f.a[i][j] = ch - '0';
        }
    q.push({f, 0});
    while (!q.empty()) {
        x = q.top();
        q.pop();
        if (!h(x.a)) {  //Judge whether it is consistent with the standard matrix
            printf("%d\n", x.t);
            return 0;
        }
        for (int i = 1; i <= 3; i++)
            for (int j = 1; j <= 3; j++)
                if (!x.a.a[i][j]) fx = i, fy = j;  //Found 0 to start diffusion
        for (int i = 0; i < 4; i++) {  //Search for the four mobile modes respectively
            int xx = fx + dx[i], yy = fy + dy[i];
            if (1 <= xx && xx <= 3 && 1 <= yy && yy <= 3) {
                swap(x.a.a[fx][fy], x.a.a[xx][yy]);
                if (!s.count(x.a))
                    s.insert(x.a),
                            q.push({x.a, x.t + 1});  //After this move, the new situation is put into the search queue
                swap(x.a.a[fx][fy], x.a.a[xx][yy]);  //Backtracking, undo operation
            }
        }
    }
    return 0;
}