Finite State Machine
Finite state machine (English: finite state machine, abbreviation: FSM), also known as finite state automaton (English: finite state automaton, abbreviation: FSA), abbreviated as state machine, is a mathematical calculation model that represents finite states, transitions and actions between these states- Wikipedia
- Elements of finite state machine
- State: there are limited states. At any time, there is only one state
- Condition: the "event" used to trigger the state transition action. When the condition is met (input), the corresponding action will be triggered
- Action: the behavior of executing state transition after the conditions are met
- Transition: transition from one state to another. The transition is generally completed by the state transition function
Let's take a look at the classic example of finite state machine: rotary gate (in this era, the gate basically doesn't use coins 😂)

If the state diagram is used, it is as follows:
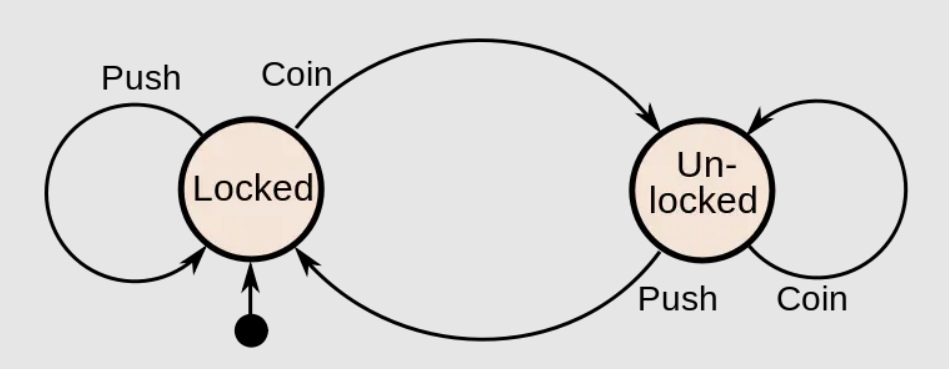
- Status: the rotary gate has only two statuses: locked and unlocked
- Condition, action and conversion: the initial state of the gate is Locked. When tourists place coins into the gate, the gate will be converted to the unlocked state. When tourists push through the gate, the gate will be converted to the Locked state.
- When the gate is in the unlocked state, it is useless to repeatedly put coins, and the state will not change. Similarly, in the locked state, it is useless to repeatedly Push the revolving door, the gate state will not change, and tourists cannot pass.
It is represented by the state transition table, as shown in the figure below:

Go realizes FSM of revolving door
The state table of the rotary gate can be converted to FSM based on the following language:
package main
import (
"bufio"
"fmt"
"log"
"os"
"strings"
)
const (
Locked = iota
Unlocked
)
const (
InputCoin = "coin"
InputPush = "push"
)
type State uint32
type StateTransitionTableDef struct {
State State
Input string
}
// Action
type TransitionFunc func(state *State)
var StateTransitionTable = map[StateTransitionTableDef]TransitionFunc{
{Locked, InputCoin}: func(state *State) {
fmt.Println("Unlocks the turnstile so that the customer can push through.")
*state = Unlocked
},
{Locked, InputPush}: func(state *State) {
fmt.Println("The turnstile has been locked.")
},
{Unlocked, InputCoin}: func(state *State) {
fmt.Println("The turnstile has been unlocked.")
},
{Unlocked, InputPush}: func(state *State) {
fmt.Println("When the customer has pushed through, locks the turnstile.")
*state = Locked
},
}
type TurnStile struct {
State State
}
func (t *TurnStile) ExecuteAction(action string) {
stateActionTupple := StateTransitionTableDef{
t.State,
strings.TrimSpace(action),
}
if transFunc := StateTransitionTable[stateActionTupple]; transFunc == nil {
fmt.Println("Unknown action, please try again!")
} else {
transFunc(&t.State)
}
}
func main() {
turnstileFSM := &TurnStile{
State: Locked, // Initial State
}
prompt(turnstileFSM.State)
reader := bufio.NewReader(os.Stdin)
for {
action, err := reader.ReadString('\n')
if err != nil {
log.Fatalln(err)
}
turnstileFSM.ExecuteAction(action)
}
}
func prompt(s State) {
m := map[State]string{
Locked: "Locked",
Unlocked: "Unlocked",
}
fmt.Printf("current state is: [%s], please input action: [coin | push]: \n", m[s])
}FSM application - lexical analysis
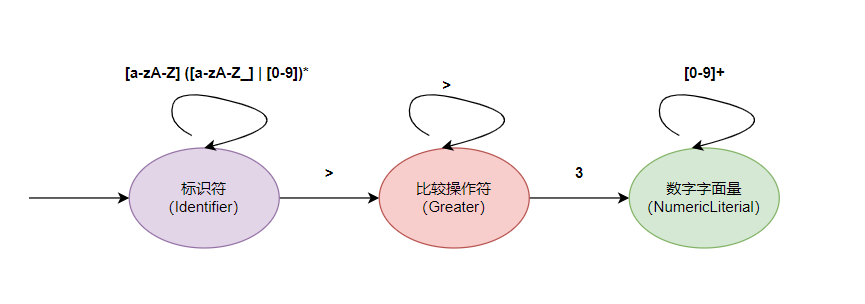
A typical application of FSM is to tokenize the lexical analysis of compiler front-end - > Lexer. For example, on tokenize in the following relational expression statement:
- blogAge > 3
When our Lexer scans relational expressions, we need to recognize that blogAge is an Identifier, > is a comparison operator, and 3 is a numeric literal. The corresponding lexical rules are as follows:
- Identifier: the first character needs to be a letter, and other characters can be numbers, letters or underscores
- Comparison operator (Greater): >
- Numeric literal: all composed of numbers
The corresponding simplified FSM state diagram is as follows:
Replicated State Machine
In the field of distributed system, state machine is used to ensure the consistency of node state. The consistency algorithm of distributed system is proposed based on Replicated State Machine.
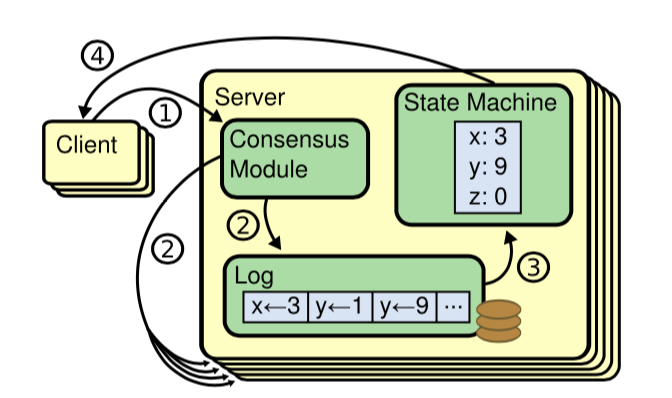
Each Server node will have a state machine. The input source of this state machine is a log storing the command sequence. For the same command input, the output of each node state machine (Deterministic Finite Automata DFA, Deterministic Finite Automata) is determined and the same.