For convolution formula

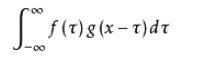
Maybe some people know, maybe some people don't know, or just know but don't understand. But whether you know the meaning of this formula or not, it doesn't affect you to realize a convolution. I won't talk about his specific mathematical meaning first, because many people speak more clearly and thoroughly than I do. What I want to tell you is how to realize the convolution operation in the deconvolution neural network

When it comes to convolution neural network, the most heard operations should be convolution, activation and pooling. Take VGG16, a classic network model, which is actually stacked through three operations: convolution + activation + pooling.

So what are they and how are they implemented? Let's talk about their specific implementation principle with numpy this time.

convolution

Convolution in neural network is to use a convolution kernel to slide on your image matrix. In the above figure, it is assumed that the gray matrix is the image matrix we input, the numbers in it represent the pixel values in the image, and the green matrix is the convolution kernel, The green area above the gray matrix is the area covered by the current convolution kernel. The sliding distance of each convolution kernel is called step size. In the figure above, the step size is 1. The specific operation is to multiply and add the convolution kernel and the corresponding position of the area covered in the image matrix. The final blue matrix is the result of this convolution.

Padding

In the above convolution operation, the size of the original matrix is 4x4, but after convolution, it becomes a 2x2 matrix. This is because the pixels on the edge will never be in the center of the convolution core, and the convolution core cannot be extended beyond the edge region.
This result is unacceptable. Sometimes we hope that the size of input and output should be consistent. To solve this problem, you can pad the original matrix before convolution, that is, fill some values on the boundary of the matrix to increase the size of the matrix, which is usually filled with "0".

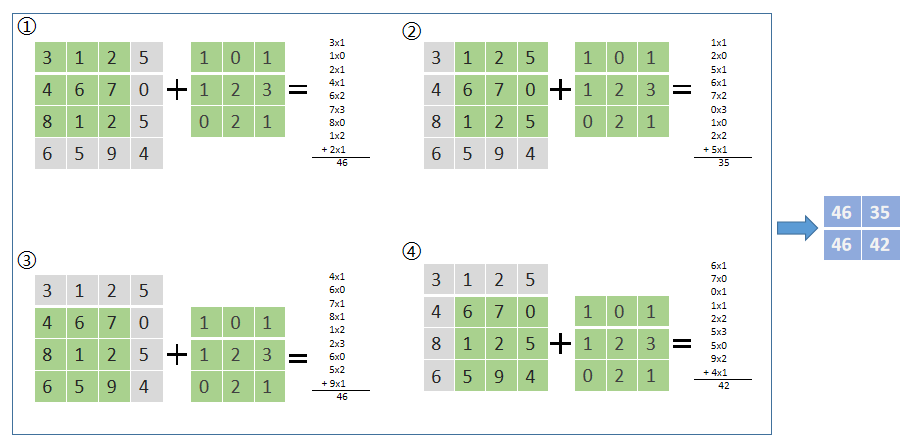
For convolution with a convolution kernel size of 3, it is usually sufficient to fill a circle of 0 on the periphery. For convolution kernels of different sizes, in order to make the size of the output image consistent, the number of circles of 0 filled on the periphery of the image is different. The filling formula is as follows:

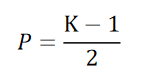
P stands for the number of circles to be filled, K stands for the side length of the convolution kernel, which is usually odd

Multichannel convolution

As we all know, a color picture has three RGB channels, that is, it has three channels. How to realize convolution in this multi-channel situation. Very simply, how many channels are there in the input image, then how many channels are there in our convolution kernel

Like the convolution operation of a single channel, slide the convolution kernel on the picture according to the corresponding channel, multiply and add the corresponding positions, and finally add up the convolution results obtained by the three channels

code implementation

#Input: input data, input_channel: number of channels of input data, out_channel: the number of channels of the output characteristic graph, kernel_size: size of convolution kernel, stripe: step size
def convolution(input,input_channel,out_channel,kernel_size,stride):
    kernel = np.random.randn(out_channel,input_channel,kernel_size,kernel_size)     #Create convolution kernel
    padding = int((kernel_size - 1) / 2)        #Calculate the size of the fill
    padding_input = []
    # Fill in the input matrix
    for i in range(input_channel):
        padding_input.append(np.pad(input[i], ((padding, padding), (padding, padding)), 'constant', constant_values=(0, 0)))
    padding_input = np.array(padding_input)
    #The size of the output matrix is calculated according to the filled input size, convolution kernel size and step size
    out_size = int((len(input[0])+2*padding-kernel_size)/stride+1)
    # Create a 0-filled output matrix
    out = np.zeros((out_channel,out_size,out_size))

    for i in range(out_channel):
        out_x = 0
        out_y = 0
        x_end = padding_input.shape[1] - padding - 1  # Convolution boundary

        x = padding
        y = padding
        while x<=x_end:
            if y>padding_input.shape[1]-padding-1:      #When the convolution kernel exceeds the right boundary, it moves down one step
                y = padding
                x = x+stride
                out_y = 0
                out_x = out_x + 1
                if x>x_end:
                    break
            #Convolution operation
            out[i][out_x][out_y] = np.sum(padding_input[:,x-padding:x+padding+1,y-padding:y+padding+1]*kernel[i])

            y = y+stride
            out_y += 1

    return out

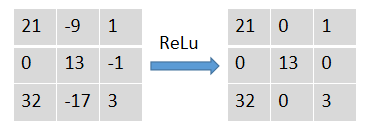
activation

It is to operate the activation function for each value in the matrix. Take relu as an example. Relu is the immobility greater than 0 and the immobility less than 0 makes it 0:

code implementation

def ReLu(input):
    out = np.maximum(0,input)
    return out

Pooling

Pooling operation is actually very similar to convolution operation, which requires a core to slide on the picture and perform some operations on the area covered by the core, but the difference is that there are numbers in the convolution core, and convolution operation is to calculate the area covered with the core. The pooled core is empty. The most common pooling operations are maximum pooling, average pooling, etc.

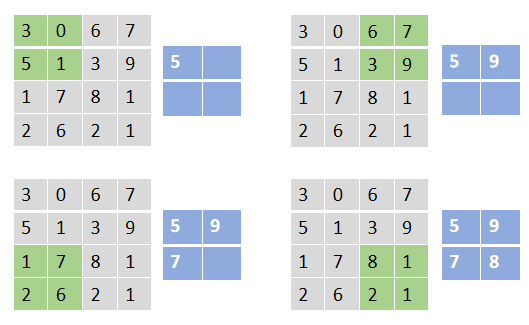
Maximum pooling

Is to select the maximum value in the area covered by the nucleus

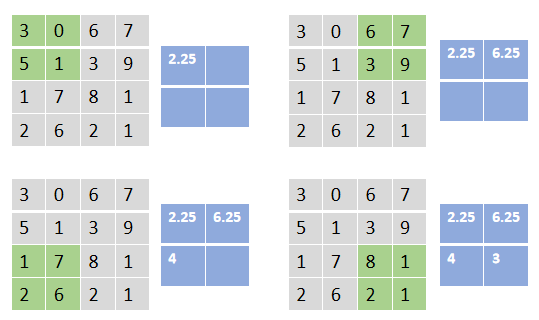
Average pooling

Is to select the average value in the area covered by the nucleus

code implementation

Take maximizing pooling as an example

#Input: input data, pooling_size: convolution kernel size, stripe: step size
def pooling(input,pooling_size,stride):
    out_size = int((len(input[0])-pooling_size)/stride+1)   #Calculate the size of the pooled output matrix
    out = np.zeros((len(input[0]),out_size,out_size))       #Initialize output matrix
    # Start pooling for each channel
    for i in range(input.shape[0]):
        out_x = 0
        out_y = 0
        in_x = 0
        in_y = 0
        #Start sliding
        while True:
            if out_y>=out_size:
                in_y = 0
                in_x+=pooling_size
                out_x+=1
                out_y = 0
                if out_x==out_size:
                    break
            #Pool operation
            out[i][out_x][out_y] = np.max(input[i,in_x:in_x+pooling_size,in_y:in_y+pooling_size])
            in_y+=pooling_size
            out_y+=1
    return out

visualization

Here are three channels of the output of a convolution operation