A thorough analysis of binary tree traversal non-recursive writing

Posted by phpQuestioner_v5.0 on Wed, 03 Jul 2019 20:07:03 +0200

Catalog (?)[+]

Preface

In the first two articles Binary Tree and Binary Search Tree Three traversals of binary trees have been involved. Recursive writing, as long as you understand the idea, a few lines of code. But non-recursive writing is not easy. Here, we summarize and thoroughly analyze their non-recursive writing. Among them, the non-recursive method of mid-order traversal is the simplest and the post-order traversal is the most difficult. Our discussion is based on the following:   

  1. //Binary Tree Node  
  2. typedef struct node  
  3. {  
  4.     int data;  
  5.     struct node* lchild;  //left child  
  6.     struct node* rchild;  //Right child  
  7. }BTNode;  

First of all, one thing is clear: non-recursive writing is bound to use stacks, which should not be explained too much. Let's first look at the middle order traversal:

Intermediate traversal

Analysis

Recursive definition of intermediate traversal: first left subtree, then root node, then right subtree. How to write non-recursive code? Bottom line: Let the code follow your thinking. What is our thinking? Thinking is the path of intermediate traversal. Suppose you have a binary tree in front of you. Now you are asked to write out its intermediate traversal sequence. If you have a thorough understanding of ordered traversal, you must first find the bottom node of the left subtree. So the following code is taken for granted:

Intermediate sequence code segment (i)

  1. BTNode* p = root;  //p points to the root of the tree  
  2. stack<BTNode*> s;  //Stack in STL  
  3. //Go all the way down to the bottom of the left subtree and save the root node to the stack while traversing  
  4. while (p)  
  5. {  
  6.     s.push(p);  
  7.     p = p->lchild;  
  8. }  

The reason for preserving the root nodes along the way is: the need for intermediate traversal, after traversing the left subtree, need to use the root node to enter the right subtree. When the code comes here and the pointer p is empty, there are two situations:


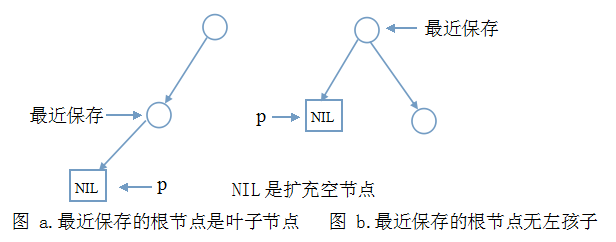
Explain:

  1. In the figure above, only the necessary nodes and edges are given. The other edges and nodes are independent of discussion and need not be drawn.
  2. You may think that the most recent saved node in Figure a is not the root node. If you've seen it Tree and Binary Tree Foundation It can be explained by using the concept of extended binary tree. In short, there is no need to tangle with this meaningless issue.
  3. The whole binary tree with only one root node can be drawn into graph a.
Think carefully, the left subtree of the binary tree, the bottom is not the above two cases? Anyway, you have to go out of the stack and access the node. This node is the first node in the ordered sequence. According to our thinking, the code should be like this:____________
  1. p = s.top();  
  2. s.pop();  
  3. cout << p->data;  

Our thinking goes on and the two pictures are treated differently:
1. In Figure a, a left child is visited, traversing in middle order, and then the root node should be visited. That's another node in Figure a. Happily, it's saved on the stack. We just need the same code as the previous one:
  1. p = s.top();  
  2. s.pop();  
  3. cout << p->data;  
  
The left child and the root are all visited, and then the right child, right? Next, just one line of code: p = p - > rchild; in the right subtree, there will be a new round of code segments (i), code segments (ii)... Until the stack is empty and p is empty.

2. Look at Figure b again, because there is no left child, the root node is the first in the middle sequence, and then directly enters the right subtree: p = p - > rchild; in the right subtree, there will be a new round of code segments (i), code segments (ii)... Until the stack is empty and p is empty.
Think here, it seems very unclear, really want to distinguish? According to the following code segment (ii) of Figure a:
  1. p = s.top();  
  2. s.pop();  
  3. cout << p->data;  
  4. p = s.top();  
  5. s.pop();  
  6. cout << p->data;  
  7. p = p->rchild;  

According to Figure b, the code snippet (ii) is like this again:
  1. p = s.top();  
  2. s.pop();  
  3. cout << p->data;  
  4. p = p->rchild;  

We can conclude that the traversal process is a loop, and a loop is made up of code segments (i), code segments (ii), until the stack is empty and p is empty.   
Different ways of dealing with it are maddening. Can they be dealt with in a unified way? It's really possible! Looking back on the extended binary tree, can each node be regarded as the root node? Then, the code only needs to be written in the same form as figure b. That is to say, the code snippet (ii) unification is as follows:

Intermediate sequence code segment (ii)

  1. p = s.top();  
  2. s.pop();  
  3. cout << p->data;  
  4. p = p->rchild;  

Speech has no basis, it has to go through the theoretical test.
The reason why the code segment (ii) of Figure a can also be written as Figure b is that because it is a leaf node, p=-= p-> rchild; then p must be empty. Is there a new round of code (i) to go through? Obviously not. (because loop conditions are not met) go straight to the code snippet (ii). Look! Finally, it's the same. Or two consecutive trips out of the stack. When you see this, think about it carefully. I'm sure you'll understand.

It's not difficult to write traversal loops.
  1. BTNode* p = root;  
  2. stack<BTNode*> s;  
  3. while (!s.empty() || p)  
  4. {  
  5.     //Code snippet (i) traverses to the bottom of the left subtree, saving the root node to the stack while traversing  
  6.     while (p)  
  7.     {  
  8.         s.push(p);  
  9.         p = p->lchild;  
  10.     }  
  11.     //Code snippet (ii) When p is empty, it indicates that it has reached the bottom of the left subtree, and then it needs to go out of the stack.  
  12.     if (!s.empty())  
  13.     {  
  14.         p = s.top();  
  15.         s.pop();  
  16.         cout << setw(4) << p->data;  
  17.         //Enter the right subtree and start a new round of left subtree traversal (this is recursive self-realization)  
  18.         p = p->rchild;  
  19.     }  
  20. }  

Think carefully, is the code written according to the direction of our thinking? With the detection of boundary conditions, the complete code of intermediate traversal in non-recursive form is as follows:

Intermediate traversal code 1  

  1. //Intermediate traversal  
  2. void InOrderWithoutRecursion1(BTNode* root)  
  3. {  
  4.     //Empty tree  
  5.     if (root == NULL)  
  6.         return;  
  7.     //Trees are not empty  
  8.     BTNode* p = root;  
  9.     stack<BTNode*> s;  
  10.     while (!s.empty() || p)  
  11.     {  
  12.         //Go all the way down to the bottom of the left subtree and save the root node to the stack while traversing  
  13.         while (p)  
  14.         {  
  15.             s.push(p);  
  16.             p = p->lchild;  
  17.         }  
  18.         //When p is empty, it means that it has reached the bottom of the left subtree, and then it needs to go out of the stack.  
  19.         if (!s.empty())  
  20.         {  
  21.             p = s.top();  
  22.             s.pop();  
  23.             cout << setw(4) << p->data;  
  24.             //Enter the right subtree and start a new round of left subtree traversal (this is recursive self-realization)  
  25.             p = p->rchild;  
  26.         }  
  27.     }  
  28. }  

Congratulations, you've finished traversing non-recursive code in intermediate order. Is it difficult to review?
The next code is essentially the same. I believe you can understand it without my explanation.

Intermediate traversal code 2

  1. //Intermediate traversal  
  2. void InOrderWithoutRecursion2(BTNode* root)  
  3. {  
  4.     //Empty tree  
  5.     if (root == NULL)  
  6.         return;  
  7.     //Trees are not empty  
  8.     BTNode* p = root;  
  9.     stack<BTNode*> s;  
  10.     while (!s.empty() || p)  
  11.     {  
  12.         if (p)  
  13.         {  
  14.             s.push(p);  
  15.             p = p->lchild;  
  16.         }  
  17.         else  
  18.         {  
  19.             p = s.top();  
  20.             s.pop();  
  21.             cout << setw(4) << p->data;  
  22.             p = p->rchild;  
  23.         }  
  24.     }  
  25. }  

Preorder traversal

Analysis

The recursive definition of preamble traversal: first root node, then left subtree, then right subtree. With the basis of intermediate traversal, I don't need to guide it like intermediate traversal.
First, we traverse the left subtree, print while traversing, and store the root node in the stack. Then we need to use these nodes to enter the right subtree to start a new cycle. It has to be repeated that all nodes can be regarded as root nodes. Write code snippets (i) according to the direction of thinking:

Preorder code segment (i)

  1. //Print while traversing and store in the stack, and then use these root nodes (don't doubt that) to enter the right subtree.  
  2. while (p)  
  3. {  
  4.     cout << setw(4) << p->data;  
  5.     s.push(p);  
  6.     p = p->lchild;  
  7. }  

Next is to go out of the stack and enter the right subtree according to the top node of the stack.

Preorder code segment (ii)

  1. //When p is empty, it means that the root and the left subtree are all traversed. It's time to enter the right subtree.  
  2. if (!s.empty())  
  3. {  
  4.     p = s.top();  
  5.     s.pop();  
  6.     p = p->rchild;  
  7. }  

Similarly, code snippets (i)(ii) constitute a complete loop. So far, it is not difficult to write a complete pre-order traversal of non-recursive writing.

Preorder traversal code 1

  1. void PreOrderWithoutRecursion1(BTNode* root)  
  2. {  
  3.     if (root == NULL)  
  4.         return;  
  5.     BTNode* p = root;  
  6.     stack<BTNode*> s;  
  7.     while (!s.empty() || p)  
  8.     {  
  9.         //Print while traversing and store in the stack, and then use these root nodes (don't doubt that) to enter the right subtree.  
  10.         while (p)  
  11.         {  
  12.             cout << setw(4) << p->data;  
  13.             s.push(p);  
  14.             p = p->lchild;  
  15.         }  
  16.         //When p is empty, it means that the root and the left subtree are all traversed. It's time to enter the right subtree.  
  17.         if (!s.empty())  
  18.         {  
  19.             p = s.top();  
  20.             s.pop();  
  21.             p = p->rchild;  
  22.         }  
  23.     }  
  24.     cout << endl;  
  25. }  

Here is another piece of code that is essentially the same:

Preorder traversal code 2

  1. //Preorder traversal  
  2. void PreOrderWithoutRecursion2(BTNode* root)  
  3. {  
  4.     if (root == NULL)  
  5.         return;  
  6.     BTNode* p = root;  
  7.     stack<BTNode*> s;  
  8.     while (!s.empty() || p)  
  9.     {  
  10.         if (p)  
  11.         {  
  12.             cout << setw(4) << p->data;  
  13.             s.push(p);  
  14.             p = p->lchild;  
  15.         }  
  16.         else  
  17.         {  
  18.             p = s.top();  
  19.             s.pop();  
  20.             p = p->rchild;  
  21.         }  
  22.     }  
  23.     cout << endl;  
  24. }  

stay Binary Tree This is a slightly different way of writing and essentially the same:

Preorder traversal code 3

  1. void PreOrderWithoutRecursion3(BTNode* root)  
  2. {  
  3.     if (root == NULL)  
  4.         return;  
  5.     stack<BTNode*> s;  
  6.     BTNode* p = root;  
  7.     s.push(root);  
  8.     while (!s.empty())  //The end condition of the loop is different from the first two  
  9.     {  
  10.         //This sentence indicates that p is always not empty in a loop.  
  11.         cout << setw(4) << p->data;  
  12.         /* 
  13.         The characteristics of stack: first in, last out 
  14.         The right subtree of the root node accessed first and then accessed 
  15.         */  
  16.         if (p->rchild)  
  17.             s.push(p->rchild);  
  18.         if (p->lchild)  
  19.             p = p->lchild;  
  20.         else  
  21.         {//The left subtree is visited, and the right subtree is visited.  
  22.             p = s.top();  
  23.             s.pop();  
  24.         }  
  25.     }  
  26.     cout << endl;  
  27. }  

Finally, enter the most difficult post-order traversal:

Postorder traversal

Analysis

Later order traversal recursive definition: first left subtree, then right subtree, then root node. The difficulty of post-order traversal is to determine whether the last visited node is located in the left subtree or the right subtree. If it is located in the left subtree, it needs to skip the root node, enter the right subtree first, and then return to the root node; if it is located in the right subtree, it directly accesses the root node. Look directly at the code, there are detailed comments in the code.

Post-order traversal code 1

  1. //Postorder traversal  
  2. void PostOrderWithoutRecursion(BTNode* root)  
  3. {  
  4.     if (root == NULL)  
  5.         return;  
  6.     stack<BTNode*> s;  
  7.     //pCur: Current Access Node, pLastVisit: Last Access Node  
  8.     BTNode* pCur, *pLastVisit;  
  9.     //pCur = root;  
  10.     pCur = root;  
  11.     pLastVisit = NULL;  
  12.     //Move pCur to the bottom of the left subtree first  
  13.     while (pCur)  
  14.     {  
  15.         s.push(pCur);  
  16.         pCur = pCur->lchild;  
  17.     }  
  18.     while (!s.empty())  
  19.     {  
  20.         //Here, pCur is empty, and has traversed to the bottom of the left subtree (as an extended binary tree, then empty, is also the left child of a tree).  
  21.         pCur = s.top();  
  22.         s.pop();  
  23.         //The premise that a root node is accessed is that no right subtree or right subtree has been accessed.  
  24.         if (pCur->rchild == NULL || pCur->rchild == pLastVisit)  
  25.         {  
  26.             cout << setw(4) << pCur->data;  
  27.             //Modify recently visited nodes  
  28.             pLastVisit = pCur;  
  29.         }  
  30.         /*Here the else statement can be replaced by other if: 
  31.         else if (pCur->lchild == pLastVisit)//If the left subtree has just been visited, it needs to enter the right subtree first (the root node needs to be stacked again) 
  32.         Because: if the above conditions fail, the following conditions must be satisfied. Think it over! 
  33.         */  
  34.         else  
  35.         {  
  36.             //The root node is re-stacked  
  37.             s.push(pCur);  
  38.             //Enter the right subtree and be sure that the right subtree is not empty  
  39.             pCur = pCur->rchild;  
  40.             while (pCur)  
  41.             {  
  42.                 s.push(pCur);  
  43.                 pCur = pCur->lchild;  
  44.             }  
  45.         }  
  46.     }  
  47.     cout << endl;  
  48. }  

Here's another way of thinking about the code. The idea is to attach a left (right) tag to each node. If the left subtree of the node has been accessed, mark it as left; if the right subtree has been accessed, mark it as right. Obviously, a node can only be accessed if its tag bit is right; otherwise, it must first enter its right subtree. See the comments in the code for more details.

Post-order traversal code 2

  1. //Define enumeration types: Tag  
  2. enum Tag{left,right};  
  3. //Customize new types to encapsulate binary tree nodes and tags together  
  4. typedef struct  
  5. {  
  6.     BTNode* node;  
  7.     Tag tag;  
  8. }TagNode;      
  9. //Postorder traversal  
  10. void PostOrderWithoutRecursion2(BTNode* root)  
  11. {  
  12.     if (root == NULL)  
  13.         return;  
  14.     stack<TagNode> s;  
  15.     TagNode tagnode;  
  16.     BTNode* p = root;  
  17.     while (!s.empty() || p)  
  18.     {  
  19.         while (p)  
  20.         {  
  21.             tagnode.node = p;  
  22.             //The left subtree of the node has been visited  
  23.             tagnode.tag = Tag::left;  
  24.             s.push(tagnode);  
  25.             p = p->lchild;  
  26.         }  
  27.         tagnode = s.top();  
  28.         s.pop();  
  29.         //If the left subtree has been visited, the right subtree needs to be accessed.  
  30.         if (tagnode.tag == Tag::left)  
  31.         {  
  32.             //Permutation marker  
  33.             tagnode.tag = Tag::right;  
  34.             //Re-stack  
  35.             s.push(tagnode);  
  36.             p = tagnode.node;  
  37.             //Enter the right subtree  
  38.             p = p->rchild;  
  39.         }  
  40.         else//If the right subtree has been accessed, the current node can be accessed  
  41.         {  
  42.             cout << setw(4) << (tagnode.node)->data;  
  43.             //Empty, go out again (this step is the difficulty of understanding)  
  44.             p = NULL;  
  45.         }  
  46.     }  
  47.     cout << endl;  
  48. }<span style="font-family: 'Courier New'; ">  </span>  

summary

There is always a huge gap between thinking and code. Usually the thinking is correct and clear, but it is not easy to write the correct code. If we want to cross this gap, there is no other way but to try and draw lessons from it.
The following are the keys to understanding the above code:
  1. All nodes can be regarded as parent nodes (leaf nodes can be regarded as empty parent nodes for two children).
  2. Compare the code of the same algorithm. The essence of the algorithm can often be seen in the differences.
  3. According to your understanding, try to modify the code. Write the code you understand. Written, that's really mastered.
Original address: http://blog.csdn.net/zhangxiangdavaid/article/details/37115355

Hot Topics

©2025 Programmer Think