t: There are n people in a circle, and everyone can choose.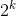Different hats, but the number of hats chosen by two neighbouring people can not be the same or 0. How many options are there?

 

Association + Reasoning

Let's assume that there are beads. We don't consider the restrictions at the beginning and at the end. We just consider the restrictions at the end. The answer is that there are many, many, and then we can calculate how many?

Now the condition is that the first one is known and the last one is to ask how many solutions there are.

Let's consider the simple case first, assuming there are only three beads in all. The first one is A, the third one is A, and the second one can only be chosen. So much more is in the middle.

Then, to promote it, let's consider that this position is, then, only one case, so we subtract one case, but this situation is still less. This position is the case, so we have to add the case that we have to determine the first position is A, the second position is, so it's always... the end. Where is the location?

The end position is also the first place to appear, that is, the third position, so we can calculate the position to the second position, that is, the third position.
 

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod=1e9+7;
ll pow_mod(ll base,ll n,int mod){
    ll ans=1;
    while(n){
        if(n&1)ans=ans*base%mod;
        base=base*base%mod;
        n>>=1;
    }
    return ans%mod;
}
int main(){
    int T;scanf("%d",&T);
    while(T--){
        ll n,k;
        scanf("%lld %lld",&n,&k);
        ll ans=0,t1=pow_mod(2,k,mod);
        ll t2=(t1-1+mod)%mod,t3=(t1-2+mod)%mod;
        ll sum=t1;
        for(int i=2;i<=n;i++)sum=sum*t2%mod;
        ans=sum;
        ll inv_t2=pow_mod(t2,mod-2,mod);
        for(int i=n-1;i;i--){
            sum=sum*inv_t2%mod;
            if((n-i)%2==0) ans=(ans-sum*t3%mod+mod)%mod;
        }
        printf("%ll\n",ans);
    }
    return 0;
}

Big Boy Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=b-1;i>=a;--i)
const int mod=1e9+7;
 
LL pow_mod(LL base,LL n,int mod) {
	LL ans=1;
	while(n) {
		if(n&1)ans=ans*base%mod;
		base=base*base%mod;
		n>>=1;
	}
	return ans%mod;
}
 
int main() {
	int T;
	scanf("%d",&T);
	while(T--) {
		LL N,K;
		scanf("%lld %lld",&N,&K);
		LL ans=0;
		LL t1=pow_mod(2,K,mod);
		LL t2=(t1-1+mod)%mod;
		LL t3=(t1-2+mod)%mod;
 
		LL sum=t1;
		for(int i=2; i<=N; i++)sum=sum*t2%mod;
		ans=sum;
 
		LL inv_t2=pow_mod(t2,mod-2,mod);
		//LL inv_
		//	printf("ans:%lld\n",ans);
		for(int i=N-1; i>=1; --i) {
			sum=sum*inv_t2%mod;
			if((N-i)%2==0) {
				LL tmp=sum*t3%mod;
				ans=(ans-tmp+mod)%mod;
				//	printf("i:%d ans:%lld sum:%lld tmp:%lld\n",i,ans,sum,tmp);
			}
		}
		printf("%lld\n",ans);
	}
	return 0;
}