Long ago, the kingdom of T prospered unprecedentedly.

In order to better manage the country, the Kingdom has built a large number of expressways to connect the capital and the major cities in the kingdom.

In order to save money, the ministers of T country have formulated an excellent construction scheme after thinking, so that any big city can reach directly from the capital or indirectly through other big cities.

At the same time, if you do not repeat passing through big cities, the scheme from the capital to each big city is unique.

J is an important Minister of state T. he patrols among major cities and observes the people's conditions.

Therefore, from one city to another has become J's most common thing.

He has a money bag for the transportation between cities.

Smart J found that if he didn't stop to repair in a city, in the process of continuous travel, the toll he spent was related to the distance he had traveled. In the kilometer from kilometer x to kilometer x+1 (x is an integer), the toll he spent was so much as x+10. In other words, it costs 11 to walk 1 km and 23 to walk 2 km.

Minister J wants to know: what is the maximum cost of all possible travel expenses when he starts from one city and doesn't rest in the middle to another city?

Input format
The first line of input contains an integer n, which represents the number of cities in Kingdom T, including the capital.

Cities are numbered from 1, and city 1 is the capital.

Next, line n − 1 describes the expressway in country T (the expressway in country T must be n − 1).

Three integers Pi, Qi and Di in each line indicate that there is a two-way expressway between city Pi and city Qi, with a length of Di km.

Output format
An integer is output to indicate the maximum travel cost of minister J.

Data range
1≤n≤105,
1≤Pi,Qi≤n,
1≤Di≤1000
Input example:
5
1 2 2
1 3 1
2 4 5
2 5 4
Output example:
135

Since the topic does not repeat passing through big cities, the scheme from the capital to each big city is unique. Therefore, we can know that the graph is a tree, and this problem is to find the diameter of the tree

Tree diameter: the longest path in the tree

1. Take any point x

2. Find the point y farthest from x

3. Start traversing from y and find the farthest point from y. The distance from the farthest point is the diameter of the tree

Prove that y must be the end of the diameter of the tree

Suppose y is not the end of the diameter of the tree. There are two cases, as shown in the figure, where uv is the diameter of the tree

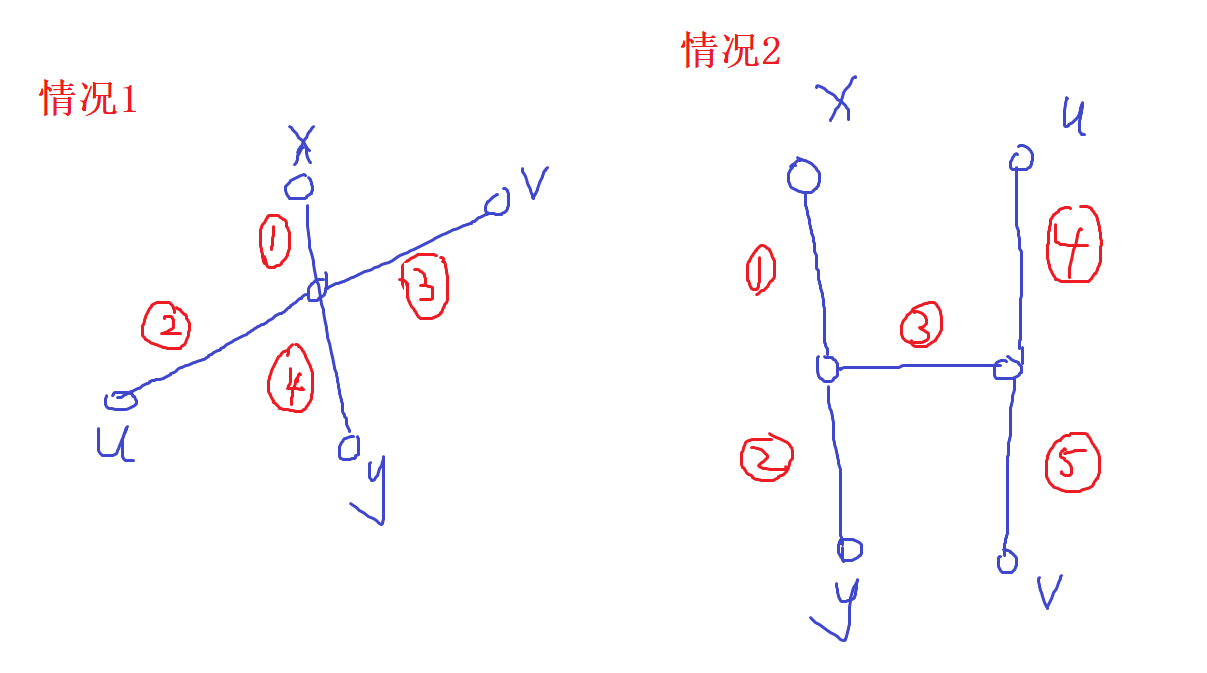
• Case 1: xy and uv have an intersection. Since the farthest point from x is y, so

With 1 + 3 < = 3 + 4

I.e. 3 < = 4

Then 3 + 2 < = 4 + 2

Since 3 + 2 is the diameter of the tree, 4 + 2 must be the diameter of the tree, so y is not the endpoint of the diameter of the tree

• Case 2:xy and uv have no intersection. Since the farthest point from x is y, so

With 1 + 2 > = 1 + 3 + 5

I.e. 2 > = 3 + 5

I.e. 2 > 5

Then 2 + 3 > 5

Then 2 + 3 + 5 > 4 + 5

Since 4 + 5 is the diameter of the tree, but there is a longer path, y is not the endpoint of the diameter of the tree

Therefore, y must be the end of the diameter of the tree

Method 1
dfs

1. Find the farthest point y from x through depth first traversal
2. Then find the longest distance with y through depth first traversal
Note: the recursive function needs to record the parent of the previous node

#include<iostream>
#include<vector>

#define x first
#define y second 

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

struct node
{
	int id, w;
};

vector<PII> g[N];
int dist[N];
int n, p, q, d;

void dfs(int u, int father, int value)
{
	dist[u] = value;
	for(int i = 0; i < g[u].size(); i ++)
	{
		if(g[u][i].x != father)
		{
			dfs(g[u][i].x, u, value + g[u][i].y);
		} 
	}
	return;
}

void solve()
{
	//Find any point x and find the farthest point y 
	dfs(1, -1, 0);
	int u = 1;
	for(int i = 1; i <= n; i ++)
	{
		if(dist[i] > dist[u])
		{
			u = i;
		}
	}
	
	//Find the distance from the farthest point of y 
	dfs(u, -1, 0);
	for(int i = 1; i <= n; i ++)
	{
		if(dist[i] > dist[u])
		{
			u = i;
		}
	}
	int s = dist[u];
	cout << s * 10 + s * (s + 1ll) / 2 << endl;
	return;
}

int main()
{
	cin >> n;
	for(int i = 1; i < n; i ++)
	{
		cin >> p >> q >> d;
		g[p].push_back(make_pair(q, d));
		g[q].push_back(make_pair(p, d));
	}
	solve();
	return 0;
}

Method 2
bfs

1. Find the farthest point y from x through breadth first traversal
2. Then find the longest distance with y through breadth first traversal

#include<iostream>
#include<queue>
#include<cstring>

using namespace std;

const int N = 100010;

int head[N * 2], edge[N * 2], Next[N * 2], ver[N * 2];
int vis[N], dist[N];
int n, p, q ,d;
int tot = 0;
int ans = 0;

void add(int u, int v, int w)
{
	ver[++ tot] = v, edge[tot] = w;
	Next[tot] = head[u], head[u] = tot;
	return;
}

int bfs(int u)
{
	queue<int> q;
	while(!q.empty()) q.pop();
	memset(vis, 0, sizeof vis);
	memset(dist, 0, sizeof dist);
	q.push(u);
	int x, maxx = 0;
	while(!q.empty())
	{
		x = q.front();
		q.pop();
		vis[x] = 1;
		for(int i = head[x]; i; i = Next[i])
		{
			int y = ver[i];
			if(vis[y]) continue;
			vis[y] = 1;
			dist[y] = dist[x] + edge[i];
			if(dist[y] > ans)
			{
				ans = dist[y];
				maxx = y;
			}
			q.push(y);
		}
	}
	return maxx;
}

int main()
{
	cin >> n;
	for(int i = 1; i < n; i ++)
	{
		cin >> p >> q >> d;
		add(p, q, d);
		add(q, p, d);
	}
	int u = bfs(1); //Find any point x find the farthest point
	int s = bfs(u); //Find the distance from the farthest point of y
	cout << ans * 10 + ans * (ans + 1ll) / 2 << endl;
	return 0;
}

Method 3
Tree dp

• Starting from any node, find the maximum length d1 and the second maximum length d2 of each node and go down through the node, then the maximum length passing through the node is d1 + d2
• dfs(u,father) indicates the maximum length d1 to find the u point

#include<iostream>
#include<queue>
#include<cstring>

using namespace std;

const int N = 100010;

int head[N * 2], edge[N * 2], Next[N * 2], ver[N * 2];
int vis[N], dist[N];
int tot = 0, ans = 0;
int n, p, q, d;

void add(int u, int v, int w) {
    ver[++ tot] = v, edge[tot] = w;
    Next[tot] = head[u], head[u] = tot;
    return ; 
}

void dp(int x) {
    vis[x] = 1;
    for(int i = head[x]; i ; i = Next[i]) {
        int y = ver[i];
        if(vis[y]) continue;
        dp(y);
        ans = max(ans, dist[x] + dist[y] + edge[i]);
        dist[x] = max(dist[x], dist[y] + edge[i]);
    }
    return ;
}

int main(void) {
    cin >> n;
    for(int i = 1; i < n; i ++) {
        cin >> p >> q >> d;
        add(p, q, d);
        add(q, p, d);
    }
    ans = 0;
    dp(1);
    cout << ans * 10 + ans * (ans + 1ll ) / 2 << endl;
    return 0;
}