Acwing Chapter V dynamic programming (I)
1, 01 knapsack problem
n items, a backpack with a capacity of v. each item has two attributes: Volume vi and value wi. Each item can only be used once. What is the maximum value of the target?

f(i,j) is selected from 1 - i articles, and the total volume does not exceed j
Set: represents all selections
State calculation

#include<iostream>
using namespace std;
const int M = 1005;
int n,m;//Number of items and backpack volume
int v[M],w[M];//Indicates the volume and value of an item
int f[M][M];//Status representation: a collection containing all selections
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
//f[0][0~M] all initialized to 0
for(int i=1;i<=n;i++) //Enumerate the first i items
{
for(int j=1;j<=m;j++)//Enumerate volumes up to j
{
if(v[i] > j) f[i][j] = f[i-1][j];//If the current backpack capacity cannot hold the ith item, the value is equal to the first i-1 item
else f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]);//Yes, you need to make a decision whether to select the ith item
}
}
cout<<f[n][m]<<endl;
}
2, Complete knapsack problem
n items, a backpack with a capacity of v. each item has two attributes: Volume vi and value wi. Each item can be used infinitely. What is the maximum value of the target?
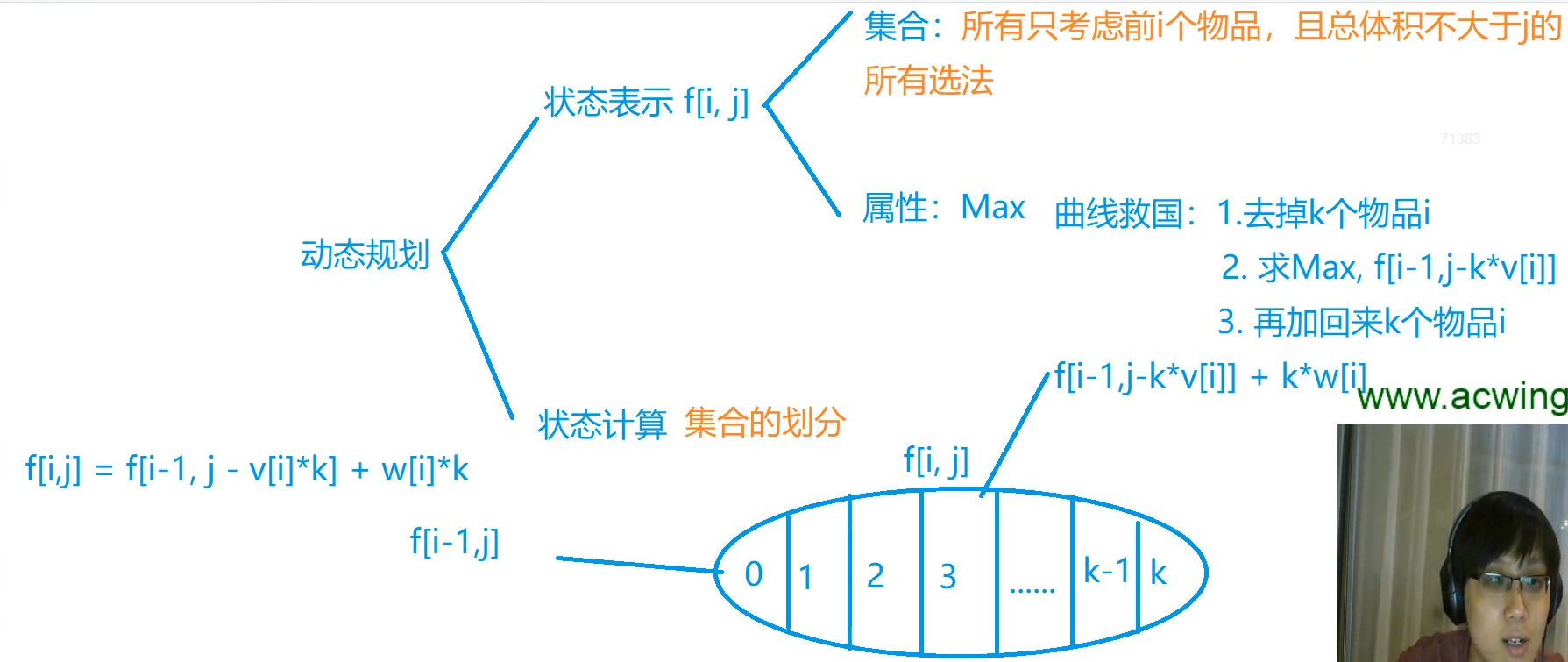
Simple approach: timeout
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N][N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i];
for(int i = 1;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
for(int k = 0;k * v[i] <= j;k++)
{
f[i][j] = max(f[i][j],f[i-1][j - k*v[i]] + k*w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
Optimization practices
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i];
for(int i = 1;i <= n;i++)
{
for(int j = v[i];j <= m;j++)//The optimized version must start enumeration from v[i]
{
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
3, Multiple knapsack problem
n items, a backpack with a capacity of v, each item has two attributes: Volume vi and value wi. There are at most si items per item (the Si of each item is different). What is the maximum value calculated by the goal?
Simple approach (0 < n, V ≤ 100, 0 < VI, WI, Si ≤ 100)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N],w[N],s[N];
int f[N][N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i = 1;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
for(int k = 0;k <= s[i] && k * v[i] <= j;k++)
{
f[i][j] = max(f[i][j],f[i-1][j - k * v[i]] + k * w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
Optimized version (0 < n ≤ 1000, 0 < V ≤ 2000, 0 < VI, WI, Si ≤ 2000)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 25005; //Up to 1000*log2000 items will be split
int n,m,v[N],w[N];
int a,b,s;//The volume, value and number of an item
int f[N];//Represents a collection of all selections
int main()
{
cin>>n>>m;
int cnt = 0;
for(int i = 1;i <= n;i++)
{
cin>>a>>b>>s;
int k = 1;//A power of current 2, which is used to split items into the number of powers of 2 as far as possible
while(k <= s)
{
cnt++; //Maintain the number of all items currently split
v[cnt] = a * k;//k items, each occupying a volume
w[cnt] = b * k;//k items, each item has b value
s -= k;//Maintain the number of currently undivided items
k = k << 1;//k shift left
}
if(s > 0)//The number of remaining items cannot be split into a larger power of 2, so the whole part is a group
{
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;//Update the number of items after the current split
for(int i = 1;i <= n;i++) //01 backpack optimization
{
for(int j = m;j >= v[i];j--)//After optimization, the enumeration must be decremented from m
{
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
4, Grouping knapsack problem
n groups of items. There are several items in each group. Select at most one item in each group. The backpack with the capacity of v has two attributes: Volume vi and value wi. Each item can only be used once. What is the maximum value of the target?
The first line has two integers N and V, separated by spaces, representing the number of item groups and backpack capacity respectively.
Next, there are N groups of data:
The first row of each group of data has an integer Si, which represents the number of items in the ith item group;
Each group of data is followed by Si rows, each row has two integers vij,wij, separated by spaces, representing the volume and value of the j-th article of the i-th article group respectively;
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N][N],w[N][N];//Volume and value of item j in group i
int s[N];//Number of items in each group
int f[N];//All selection sets
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++)
{
cin>>s[i];//Number of items in group i
for(int j = 1;j<=s[i];j++)
{
cin>>v[i][j]>>w[i][j];//Volume and value of item j in group i
}
}
for(int i = 1;i <= n;i++)//The sequence number of the enumeration group
{
for(int j = m;j >= 1;j--)//After optimization, the enumeration knapsack volume must be decremented from m
{
for(int k = 1;k <= s[i];k++)//Enumerate the k-th item in a group
{
if(v[i][k] <= j)//If the volume of item k in group i is less than the backpack volume
{
f[j] = max(f[j],f[j - v[i][k]] + w[i][k]);//Only those with greater value can choose
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
5, Linear DP
898. Digital triangle
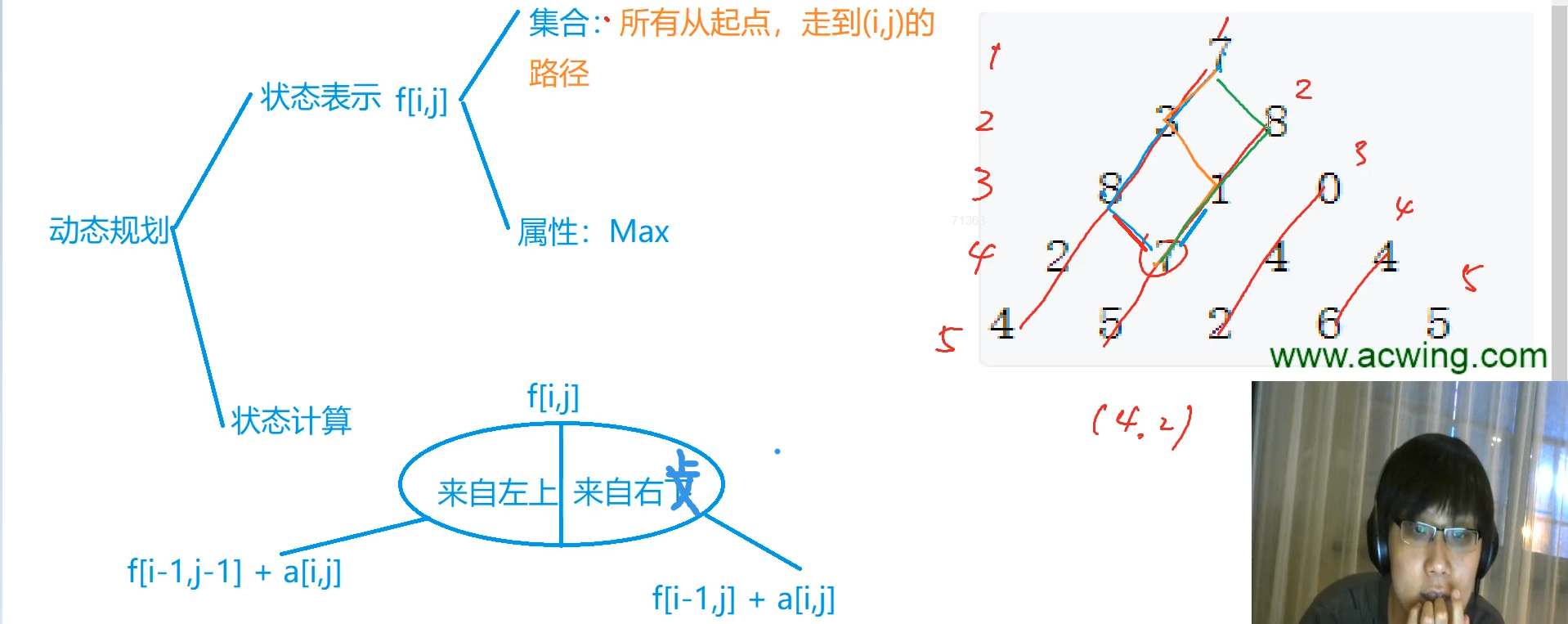
O(N^2)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 505,INF = 0x3f3f3f3f;
int a[N][N];//Digital triangle
int f[N][N]; //Status indication: the current maximum value of the sum of the numbers in row i and column j
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
memset(f,-INF,sizeof f);//All scheme representation arrays must be initialized to negative infinity
//Because the boundary number will be out of bounds when calculating the state, negative infinity can solve this kind of problem
f[1][1] = a[1][1];//The sum maximum of the first number must be itself
for(int i=1;i<=n;i++) //Enumerate calculations from the second line
{
for(int j=1;j<=i;j++)
{
f[i][j] = max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);//Taking the maximum sum of the numbers of the upper left path and the upper right path plus itself is the answer
}
}
int Max = -0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
Max = max(Max,f[n][i]);//The answer takes the maximum value in the last line
}
cout<<Max<<endl;
return 0;
}
895. Longest ascending subsequence
O(N^2)

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
int n,a[N];
int f[N];
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>a[i];
}
for(int i = 1;i <= n;i++)
{
f[i] = 1; //Initialization, there is only a[i] in the set
for(int j = 1;j < i;j++) //Enumerating from 1~i-1, if j is smaller than I, consider merging f[j] set with a[i] according to the number
{
if(a[j] < a[i])
{
f[i] = max(f[i],f[j] + 1);
}
}
}
int res = -1;
for(int i = 1;i<=n;i++) //Compare each set and select the one with the largest number
{
res = max(res,f[i]);
}
cout<<res<<endl;
return 0;
}
Find the set elements of the specific scheme
for(int i = 1;i <= n;i++)
{
f[i] = 1; //Initialization, there is only a[i] in the set
g[i] = 0;//Indicates that there is only a[i] itself in the set
for(int j = 1;j < i;j++) //Enumerating from 1~i-1, if j is smaller than I, consider merging f[j] set with a[i] according to the number
{
if(a[j] < a[i])
{
if(f[i] < f[j] + 1)
{
f[i] = f[j] + 1;
g[i] = j;
}
}
}
}
int res = -1,k;
for(int i = 1;i <= n;i++) //Compare each set and select the one with the largest number
{
if(res < f[i])
{
res = f[i];
k = i;
}
}
while(k!=0)
{
printf("%d ",a[k]);
k = g[k];//Recurrence
}
puts("");
cout<<res<<endl;
896. Longest ascending subsequence II
Given a sequence with length N, find the longest length of the subsequence with strictly monotonically increasing value.
Input format
The first line contains the integer N.
The second line contains N integers, representing the complete sequence.
Output format
Outputs an integer representing the maximum length.
Data range
1≤N≤100000,
− 109 ≤ number in sequence ≤ 109
Monotone stack + dichotomy (O (NlogN))
#include<iostream>
using namespace std;
const int N = 1e5+10;
int a[N],stk[N],top=0;
int n;
int find(int x) //The minimum number greater than or equal to x in the binary search monotone stack
{
int l = 1,r = top;
while(l <= r)
{
int mid = l+r>>1;
if(stk[mid] >= x)
{
r = mid - 1;
}
else l = mid + 1;
}
return l;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
stk[++top] = a[0]; //The first number is put on the stack
for(int i = 1;i < n;i++)
{
if(a[i] > stk[top]) stk[++top] = a[i]; //If the current number is greater than the top of the stack, enter the stack
else //Otherwise, find the minimum number greater than or equal to a[i] in the stack and replace it with a[i]
{
int p = find(a[i]);
stk[p] = a[i];
}
}
// for(int i = 1;i<=top;i++)
// {
// cout<<stk[i]<<" ";
// }
cout<<top<<endl; //Number of elements in the output stack
return 0;
}
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
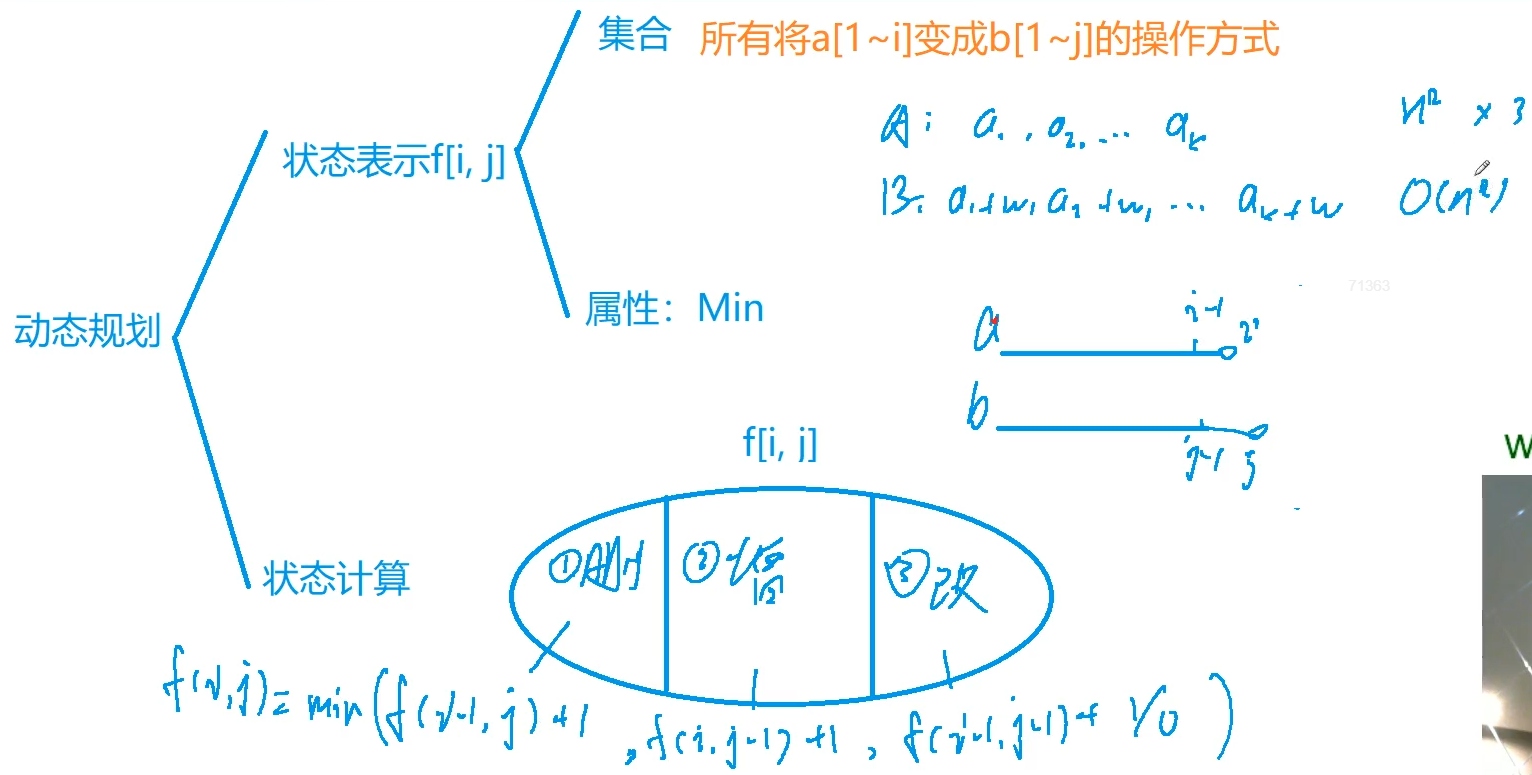
char a[N],b[N];
int f[N][N];//The first i letters of a string are transformed into the minimum operation times of the first j letters of b string by transformation operation
int n,m;
int main()
{
cin>>n>>a+1;
cin>>m>>b+1;
//Initialize operations to handle boundary problems
for(int i = 1;i <= n;i++)
{
f[i][0] = i; //To change the first i letter in a string to 0, i deletion operations are required
}
for(int i = 1;i <= m;i++)
{
f[0][i] = i;//To change the empty string of a string into the first i letter in b, i addition operations are required
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j] = min(f[i-1][j] + 1,f[i][j-1] + 1); //The left indicates deletion, provided that a[1~i-1] is equal to b[1~j];
//The right indicates the addition operation, provided that a[1~i] is equal to b[1~j-1]
if(a[i] == b[j]) f[i][j] = min(f[i][j],f[i-1][j-1]);//Equality does not require substitution, provided that a[1~i-1] is equal to b[1~j-1]
else f[i][j] = min(f[i][j],f[i-1][j-1] + 1); //Inequality requires substitution if a[1~i-1] is equal to b[1~j-1]
}
}
cout<<f[n][m]<<endl;
return 0;
}
897. Longest common subsequence


If two characters are equal, they can be directly transferred to f[i-1][j-1]. If they are not equal, one of the two characters must be discarded. You can take max for the two states of F [I-1] [J] and f [i] [J-1] to transfer.
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
char a[N],b[N];
int n,m;
int f[N][N]; //Set representation: the common subsequence in the first i letters of the first string and the first j letters of the second string. Attribute: the maximum value of the sequence length
int main()
{
cin>>n>>m;
scanf("%s%s",a+1,b+1);
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
if(a[i] == b[j]) //If the i-th letter of the first string is equal to the j-th letter of the second string, it can be directly transferred to f[i-1][j-1]
{
f[i][j] = max(f[i][j],f[i-1][j-1] + 1);
} //If they are not equal, one of the two characters must be discarded, and the two states of F [I-1] [J] and f [i] [J-1] can be transferred by taking max.
else f[i][j] = max(f[i][j-1],f[i-1][j]);
}
}
cout<<f[n][m]<<endl;
return 0;
}
6, Interval DP
thinking
f[i,j] represents the minimum cost of merging all piles i to j into one pile
State calculation: all piles i to j are merged into one pile. The merging method is divided into several categories, and the dividing line is merged in the last step
Minimum cost on the left + minimum cost on the right + cost of the last step

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 305,INF = 0x3f3f3f3f;
int f[N][N],a[N],s[N];
int n;
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>a[i];
s[i] = s[i-1] + a[i]; // Calculate prefix and
}
//Since the state recursion requires that the result of the sub interval has been obtained during the calculation, the interval length must be enumerated from small to large
for(int len = 2;len <= n;len++) //When the interval length is 1, there is no need to merge, and the cost is 0, so the length is enumerated from 2
{
for(int i = 1;i + len - 1 <= n;i++)
{
int l = i, r = i + len - 1;//Left and right boundary
f[l][r] = INF;//Calculate the minimum value, so the initialization f[l][r] must be infinite
for(int k = l;k < r;k++) //Demarcation point enumeration [l,r-1]
{
f[l][r] = min(f[l][r],f[l][k] + f[k+1][r] + s[r] - s[l-1]);
}
}
}
cout<<f[1][n]<<endl;
return 0;
}
7, Digital statistics DP
338. Counting issues
count(n,x): the number of times x occurs in 1-n
Total number of occurrences of X from a to b = count(b,x) - count(a-1,x)
Classified discussion

# include <iostream>
# include <cmath>
using namespace std;
int dgt(int n) // Calculate the number of bits of integer n
{
int res = 0;
while (n) ++ res, n /= 10;
return res;
}
int cnt(int n, int i) // Calculates how many times the number i appears in an integer from 1 to n
{
int res = 0, d = dgt(n);
for (int j = 1; j <= d; ++ j) // How many times does the number i appear on the j-th bit from right to left
{
// l and r are integers on the left and right of bit J (abc and EFG in the video); DJ is the j-th digit
int p = pow(10, j - 1), l = n / p / 10, r = n % p, dj = n / p % 10;
// Calculate the case where the integer on the left of bit j is less than l (XXX = 000 ~ ABC - 1 in the video)
if (i) res += l * p;
if (!i && l) res += (l - 1) * p; // If i = 0, the left high order cannot be all 0 (XXX = 001 ~ ABC - 1 in the video)
// Calculate the case where the integer on the left of bit j is equal to l (XXX = ABC in the video)
if ( (dj > i) && (i || l) ) res += p;
if ( (dj == i) && (i || l) ) res += r + 1;
}
return res;
}
int main()
{
int a, b;
while (cin >> a >> b , a)
{
if (a > b) swap(a, b);
for (int i = 0; i <= 9; ++ i) cout << cnt(b, i) - cnt(a - 1, i) << ' ';
cout << endl;
}
return 0;
}
8, State compression DP
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20,M=1<<N;
int f[M][N],w[N][N];//w is a graph
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>w[i][j];
memset(f,0x3f,sizeof(f));//Initialize to infinity because a minimum value is required
f[1][0]=0;//Since zero is the starting point, f[1][0]=0;
for(int i=0;i<1<<n;i++)//i indicates all cases
for(int j=0;j<n;j++)//j indicates which point to go to
if(i>>j&1)
for(int k=0;k<n;k++)//k represents the shortest distance to k before reaching j
if(i>>k&1)
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//Update shortest distance
cout<<f[(1<<n)-1][n-1]<<endl;//Indicates that all points have passed and the end point is the shortest distance of n-1
//The priority of bit operation is lower than '+' - ', so parentheses should be used if necessary
return 0;
}
9, Tree DP
285. A dance without a boss

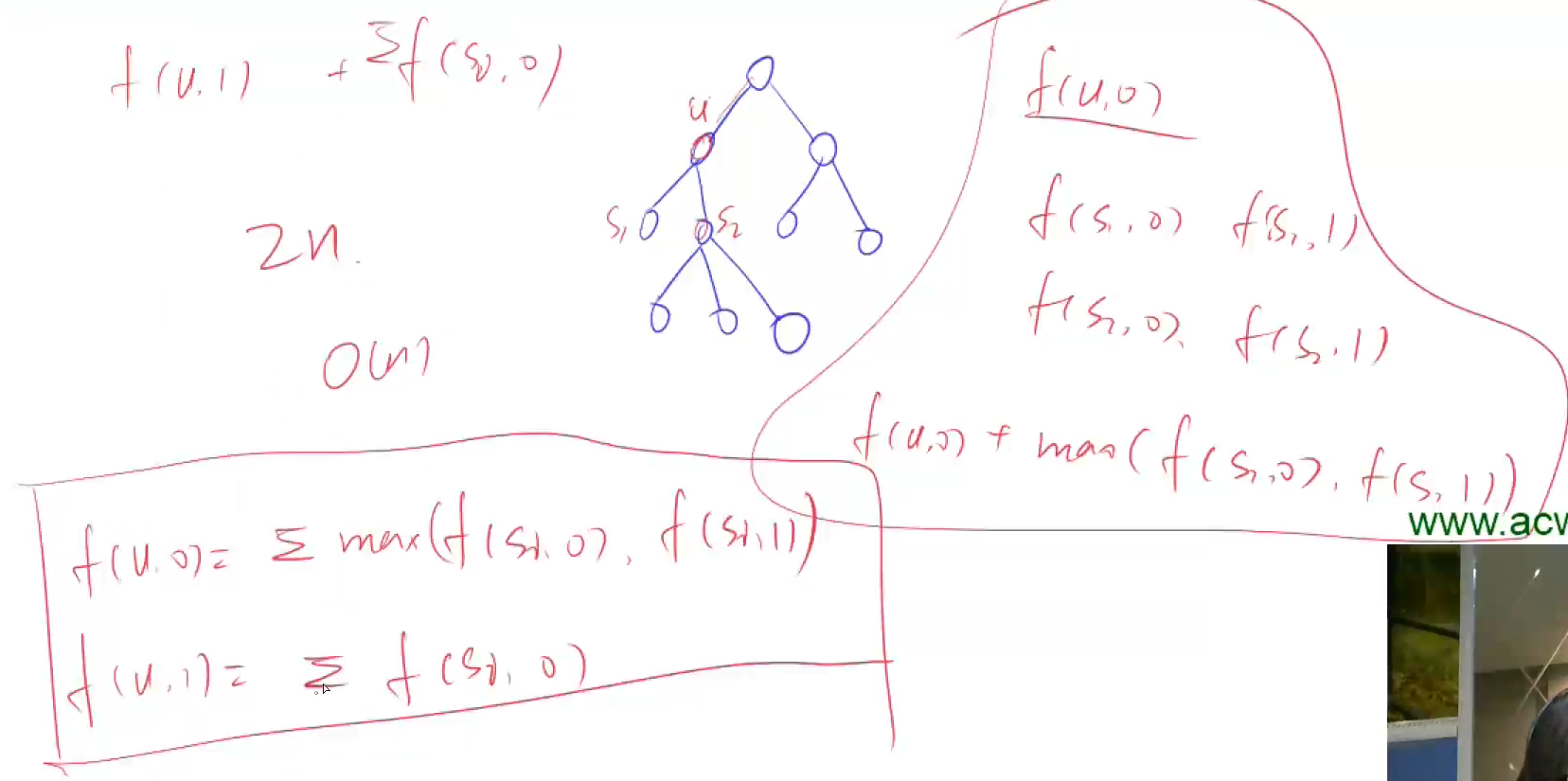
If everyone has only two states, set dp[0][i]dp[0][i] as the maximum happiness that his subordinates can get if the ith person doesn't come;
dp[1][i]dp[1][i] is the maximum happiness that his subordinates can get when the ith person comes.
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010;
int happy[N];
int h[N],e[N],ne[N],idx;
int f[N][2];
int n;
bool has_father[N]; //Parent node or not
void add(int a,int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
f[u][1] = happy[u]; //When this person comes, first add his own happiness value
for(int i = h[u];i!=-1;i=ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += max(f[j][0],f[j][1]); //The maximum happiness that can be obtained if the person doesn't come and the subordinates come or don't come
f[u][1] += f[j][0]; //If this person comes, his subordinates will not come
}
}
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>happy[i];
}
memset(h,-1,sizeof h);
int a,b;
for(int i = 0;i< n-1;i++) //Build a tree
{
cin>>a>>b;
add(b,a);
has_father[a] = true;
}
int root = 1;
while(has_father[root]) root++; //Root node found
dfs(root);
cout<<max(f[root][0],f[root][1])<<endl; //Choose the root or not, whichever is greater
return 0;
}
10, Memory search
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 310;
int h[N][N],f[N][N];
int n,m,res;
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
int dp(int x,int y)
{
int &v = f[x][y]; //Alias f[x][y] by reference
if(v!=-1) return v; //If it is found that the current location has been searched, it will be returned directly
v = 1;//Initialization, the minimum number of steps is 1
for(int i = 0;i < 4;i++)
{
int a = x + dx[i];
int b = y + dy[i];
if(a>=0 && a<n && b>=0 && b<m && h[x][y] > h[a][b]) //Try to search if you meet the requirements
{
v = max(v,dp(a,b) + 1);//Remember: you must dp search here, not available f[i][j]
}
}
return v; //Be sure to return f[x][y]
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>h[i][j];
}
}
memset(f,-1,sizeof f); //Memory search indicates that it has not been searched
for(int i = 0;i < n;i++)
{
for(int j = 0;j < m;j++)
{
res = max(res,dp(i,j)); //Remember: you must dp search here, not available f[i][j]
}
}
cout<<res<<endl;
return 0;
}