Addition (insertion) and deletion of red black trees

 

☼ introduction to red and black trees:

-----------Morphologically, it is a special binary search tree [specially reflected in color, and logically, it is equivalent to a fourth-order B tree]

 

❀ how is a red black tree equivalent to a fourth-order B tree--------- To turn the red black tree into a B-tree: you need to merge the red node and the black node (black is the root [also the intermediate element]).

✿ red black -- > b tree: there are four types of nodes: ① red black red, ② red black, ③ black red and ④ black

◼ Red black trees must meet the following five properties: 1. The node is RED or BLACK 2. The root node is BLACK 3. All leaf nodes (external nodes and empty nodes) are BLACK 4. All child nodes of red node are BLACK: The parent of RED node is BLACK ‡ there cannot be 2 consecutive RED nodes on all paths from the root node to the leaf node 5. All paths from any node to the leaf node contain the same number of BLACK nodes

 

1, Addition (insertion) of red black tree node -- the addition must be added to the position of - B tree leaf sub node:

(1)       The leaf nodes of level 4 B trees are generally in the following four cases:

①     Red < --- black -- > Red     ② Red < --- black         ③ Black -- > Red       ④ Black

(2) Classified discussion:

(2-1) when the parent node is black (there are four cases), insert it directly; [it may be the first node root (remember to dye black root)];

(2-2) the remaining 8 cases are divided according to whether the uncle node is red:

(2-2-1) uncle is red. Take chestnuts for example:    Red (newly inserted) < --- red < --- black [root] - > Red (for level 4 B trees, overflow occurs, so it needs to be split, the root (dyed red) goes up, and then the parent node and uncle node are dyed black); Namely:

 

 

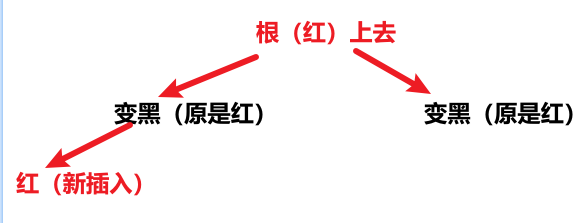
(2-2-2) uncle is not red. Take chestnuts for example:    Red (newly inserted) < --- red < --- black [root]: in order to meet property 4 of the definition of red black tree:

   Red (newly inserted) < --- red (turning black) < --- black [root] (turning red, because the node combination of B tree is red, black and red (there is only one black as the root of the intermediate element))

   ●   Now it needs to be modified: the black in the middle is the root, and the direction of < --- needs to be modified as follows:

  Red (newly inserted) < --- red (turning black) [root] - > black [root] (turning red)

[observe the current situation, modify this modification to conform to the right rotation, and then observe that it is actually consistent with the LL type principle of AVL]

 

❀ the processing code after adding the whole red black tree is as follows:

    @Override
    protected void afterAdd(Node<E> node) {
        // Judge parent node
        Node<E> parent = node.parent;
        // The root is added [when adding the first node]/ Or overflow to the root node
        if (parent == null) {
            black(node);
            return;
        }
        // If the parent node is black, it does not need to be processed and returns directly
        if (isBlack(parent))
            return;

        // If Uncle node is red[B Tree overflow]
        Node<E> uncle = parent.sibling();
        Node<E> grand = red(parent.parent);
        if (isRed(uncle)) {
            // Dye black father and uncle, dye grandfather red, which is equivalent to the newly inserted node
            black(uncle);
            black(parent);
//            red(grand);
//            afterAdd(grand);
            // ① When overflow occurs, it should also be dyed red
//            afterAdd(red(grand));
            afterAdd(grand);
            return;
        }
        //Take a look, optimize the code, extract the jointly owned from the outside, and so on
        // Come here, uncle is not red
        if (parent.isLeftChild()) { // L
            // ② When rotating, you should also dye the nodes red
//            red(grand);
            
            if (node.isLeftChild()) { // LL
                //Dye black parent node, dye red grandfather node
                black(parent);
//                red(grand);
                //Dextral
//                rotateRight(grand);
            } else { // LR
                //Dye yourself red and dye yourself black
                black(node);
//                red(grand);
                //Left back right rotation
                rotateLeft(parent);
//                rotateRight(grand);
            }
            
            rotateRight(grand);
        } else { // R
            // ② When rotating, you should also dye the nodes red
//            red(grand);
            
            if (node.isLeftChild()) { // RL
                //Dye yourself red and dye yourself black
                black(node);
//                red(grand);
                //Left back right rotation
                rotateRight(parent);
//                rotateLeft(grand);
            } else { // RR
                //Dye black parent node, dye red grandfather node
                black(parent);
//                red(grand);
                //Sinistral
//                rotateLeft(grand);
            }
            
            rotateLeft(grand);
        }
    }