Advanced data structure (Ⅳ) Binary Sort Tree (BST)
Basic concepts
This data structure is composed of nodes. The links contained in nodes can be empty (null) or point to other nodes. In a binary tree, each node can only have one parent node (with one exception, that is, the root node, which has no parent node), and each node has only two left and right links, pointing to its left and right child nodes respectively. The two links of each node point to an independent sub binary tree or empty link. In the binary search tree, each node also contains a key and a value, and there is also order between the keys to support the search of colleges and universities.
Definition: a binary search tree (BST) is a binary tree, in which each node contains a Comparable key (and associated value), and the key of each node is greater than that of any node in its left subtree and less than that of any node in its right subtree.
The API of binary lookup tree with int type as key and String type as value is as follows
class BST<Key extends Comparable<Key>, Value>
-------------------------------------------------------------------------------------
Node root; Root node
int size(Node x); Return to node x Is the subtree size of the root node
Value get(Key key) Return key key Corresponding value
void put(Key key, Value val) Insert key value pair{key : val}
Key min() Return to minimum key
Key max() Return maximum key
Key floor(Key key) Round down (return less than or equal to) key (maximum value of)
Key ceiling(Key key) Round up (return greater than or equal to) key (minimum value of)
Key select(int k) The return ranking is k Key of
int rank(Key key) Return key key Ranking of
Iterable<Key> keys(Key lo, Key hi) Return search (return all key values within the specified range)
void deleteMin() Delete minimum key
void deleteMax() Delete max key
void delete (Key key) Delete key key
Basic implementation
🎈
Data representation
We define a private class nested to represent a node on the binary lookup tree. Each node contains a key, a right link and a counter. The left link points to a binary search tree composed of all keys smaller than the node, and the right link points to a binary search tree composed of all keys larger than the node. The variable N gives the total number of nodes of the subtree with this node as the root.
s
i
z
e
(
x
)
=
s
i
z
e
(
x
.
l
e
f
t
)
+
s
i
z
e
(
x
.
r
i
g
h
t
)
+
1
size(x)=size(x.left)+size(x.right)+1
size(x)=size(x.left)+size(x.right)+1
class BST<Key extends Comparable<Key>, Value> {
private Node root; //Root node of binary lookup tree
private class Node{
private Key key; //key
private Value val; //value
private Node left, right; //Link to subtree
private int N; //The total number of nodes in the subtree with this node as the root
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
public int size() {
return size(root);
}
private int size(Node x) {
if (x == null) {
return 0;
} else {
return x.N;
}
}
}
A binary lookup tree represents a set of keys (and their corresponding values), and the same set can be represented by multiple different binary lookup trees. If we project all the keys of a binary search tree onto a straight line to ensure that the keys in the left subtree of a node appear on its left and the keys in the right subtree appear on its right, then we can get an ordered key column.
🎈
lookup
In general, looking up a key in the symbol table can get two results. If the node containing the key exists in the table, our search hits, and then returns the corresponding value. Otherwise, the lookup misses (and returns null). According to the recursive structure of data representation, we can immediately get the recursive algorithm to find a key in the binary search tree: if the tree is empty, the search misses; If the key to be searched is equal to the key of the root node, the search hits, otherwise we will continue to search (recursively) in the appropriate subtree. If the searched key is small, select the left subtree, and if it is large, select the right subtree.
/*** Search***/
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {
//Find and return the value corresponding to the key in the subtree with x as the root node
//null if not found
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return get(x.left, key);
} else if (cmp > 0) {
return get(x.right, key);
} else {
return x.val;
}
}
🎈
insert
Binary search tree insertion is almost as difficult as search. If the tree is empty, a new node containing the key value pair is returned; If the searched key is less than the key of the root node, continue to search and insert the key in the left subtree, otherwise insert the key in the right subtree.
/*** Insert***/
public void put(Key key, Value val) {
//Find the key and update its value if found. Otherwise, create a new node for it
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {
//If the key exists in the subtree with x as the root node, update its value;
//Otherwise, a new node with key and val as key value pairs will be inserted into the subtree
if (x == null) {
return new Node(key, val, 1);
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
x.left = put(x.left, key, val);
} else if (cmp > 0) {
x.right = put(x.right, key, val);
} else {
x.val = val;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
}
Proposition: in the binary search tree constructed by N random keys, the average number of comparisons required to find hits is ~ 2lnN (about 1.39lgN)
The cost of finding random keys in binary search tree is about 39% higher than that of binary search.
Proposition: in the binary search tree constructed by N random keys, the average number of comparisons required for insertion and search misses is ~ 2lnN (about 1.39lgN)
🎈
Order related methods
An important reason why binary lookup tree is widely used is that it can maintain the order of keys, so it can be used as the basis of many methods in the ordered symbol table API. This enables the use case of the symbol table to access key value pairs not only through keys, but also through the relative order of keys.
🎈
Minimum and maximum keys
If the left link of the root node is empty, the smallest key in a binary search tree is the root node; If the left link is not empty, the minimum key in the tree is the minimum key in the left subtree, and the display can be realized by recursive operation.
The method of finding the maximum key is similar, but it is to find the right subtree.
Minimum key
/*** Minimum key***/
public Key min() {
if (root == null) {
return null;
}
return min(root).key;
}
private Node min(Node x) {
if (x.left == null) {
return x;
}
return min(x.left);
}
Maximum key
/*** Maximum key***/
public Key max() {
if (root == null) {
return null;
}
return max(root).key;
}
private Node max(Node x) {
if (x.right == null) {
return x;
}
return max(x.right);
}
🎈
Round up and round down
If the given key is less than the key of the root node of the binary search tree, the maximum key floor(key) less than or equal to the key must be in the left subtree of the root node; If the given key is greater than the root node of the binary lookup tree, the maximum key less than or equal to the key will appear in the right subtree only when there are nodes less than or equal to the key in the right subtree of the root node, otherwise the root node is the maximum key less than or equal to the key. This description illustrates the recursive implementation of the floor() method and also proves recursively that it can calculate the expected results. Changing "left" to "right" (and changing less than to greater than) can get the algorithm of ceiling().
Rounding down floor()
/*** Round down***/
public Key floor(Key key) {
Node x = floor(root, key);
if (x == null) {
return null;
}
return x.key;
}
private Node floor(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0) {
return x;
}
if (cmp < 0) {
return floor(x.left, key);
}
Node t = floor(x.right, key);
if (t != null) {
return t;
} else {
return x;
}
}
Rounding up
/**** Round up**/
public Key ceiling(Key key) {
Node x = ceiling(root, key);
if (x == null) {
return null;
}
return x.key;
}
private Node ceiling(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0) {
return x;
}
if (cmp > 0) {
return ceiling(x.right, key);
}
Node t = ceiling(x.left, key);
if (t != null) {
return t;
} else {
return x;
}
}
🎈
Select operation
The selection operation of binary lookup tree is similar to that of array selection based on segmentation. The subtree node counter variable N maintained in each node of the binary lookup tree is used to support this operation.
Suppose we want to find the key ranked K (that is, there are exactly k keys smaller than it in the tree). If the number of nodes t in the left subtree is greater than k, then we continue (recursively) to find the key ranking K in the left subtree; If t equals K, we return the key in the root node; If t is less than k, we will (recursively) find the key ranked (k-t-1) in the right subtree. This description not only explains the recursive implementation of the select() method, but also proves its correctness.
/*** Select operation (return key ranked k)***/
public Key select(int k) {
if (root == null) {
return null;
}
return select(root, k).key;
}
private Node select(Node x, int k) {
//Return the node ranked k
if (x == null) {
return null;
}
//Note: int t = size(x.left) in the book;
//Personally, I think the current node should be added here, i.e. + 1 (please correct if you have any suggestions)
int t = size(x.left) + 1;
if (t > k) {
return select(x.left, k);
} else if (t < k) {
return select(x.right, k - t - 1);
} else {
return x;
}
}
🎈
ranking
The rank() method is the inverse of the select() method, which returns the ranking of a given key. Its implementation is similar to select(): if the given key is equal to the key of the root node, we return the total number of nodes in the left subtree, t; If the given key is smaller than the root node, we will return the ranking of the key in the left subtree (recursive calculation); If the given key is greater than the root node, we will return t+1 (root node) plus its ranking in the right subtree (recursive calculation).
/*** Returns the ranking of the given key***/
public int rank(Key key) {
if (root == null) {
return 0;
}
return rank(root, key);
}
private int rank(Node x, Key key) {
//Returns the number of keys smaller than x.key in the subtree with X as the root node
if (x == null) {
return 0;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return rank(x.left, key);
} else if (cmp > 0) {
return 1 + size(x.left) + rank(x.right, key);
} else {
//If you return the ranking of a given key, I think you should + 1 here, otherwise you can + 1 after the return statement called above
//Here is return size(x.left) (please correct if you have any suggestions);
return size(x.left) + 1;
}
}
🎈
Range lookup
To implement the keys() method that can return the key of a given range, we first need a basic method to traverse the binary search tree, which is middle order traversal. To illustrate this method, let's first see how we can print out all the keys in the binary search tree in order. To do this, we should first print out all the keys in the left subtree of the root node (according to the definition of binary search tree, they should be less than the keys of the root node), then print out the keys of the root node, and finally print out all the keys in the right subtree of the root node (according to the definition of binary search tree, they should be greater than the keys of the root node).
In order to ensure that all keys within the specified range in the subtree with a given node as the root join the queue, we will (recursively) find the left subtree of the root node, then find the root node, and then (recursively) find the right subtree of the root node.
/*** Range lookup (returns all key values within a given range)***/
public Iterable<Key> keys() {
return keys(min(), max());
}
public Iterable<Key> keys(Key lo, Key hi) {
Queue<Key> queue = new LinkedList<Key>();
keys(root, queue, lo, hi);
return queue;
}
private void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
if (x == null) {
return;
}
int cmplo = lo.compareTo(x.key);
int cmphi = hi.compareTo(x.key);
if (cmplo < 0) {
keys(x.left, queue, lo, hi);
}
if (cmplo <= 0 && cmphi >= 0) {
queue.offer(x.key);
}
if (cmphi > 0) {
keys(x.right, queue, lo, hi);
}
}
Methods related to deletion
🎈
Delete minimum key
The most difficult method to implement in binary lookup tree is the delete() method, which deletes a key value pair from the symbol table. Before that, let's consider the deletemin () method (delete the key value pair corresponding to the smallest key). For deleteMin(), we need to go deep into the left subtree of the root node until we meet an empty link, and then point to the right subtree of the node (just return its right link in the recursive call). At this point, it will be cleaned up by the garbage collector. After deleting a node, the standard recursive code we give will correctly set the link of its parent node and update the counter values of all nodes on its path to the root node. The detailed process is shown in the figure below
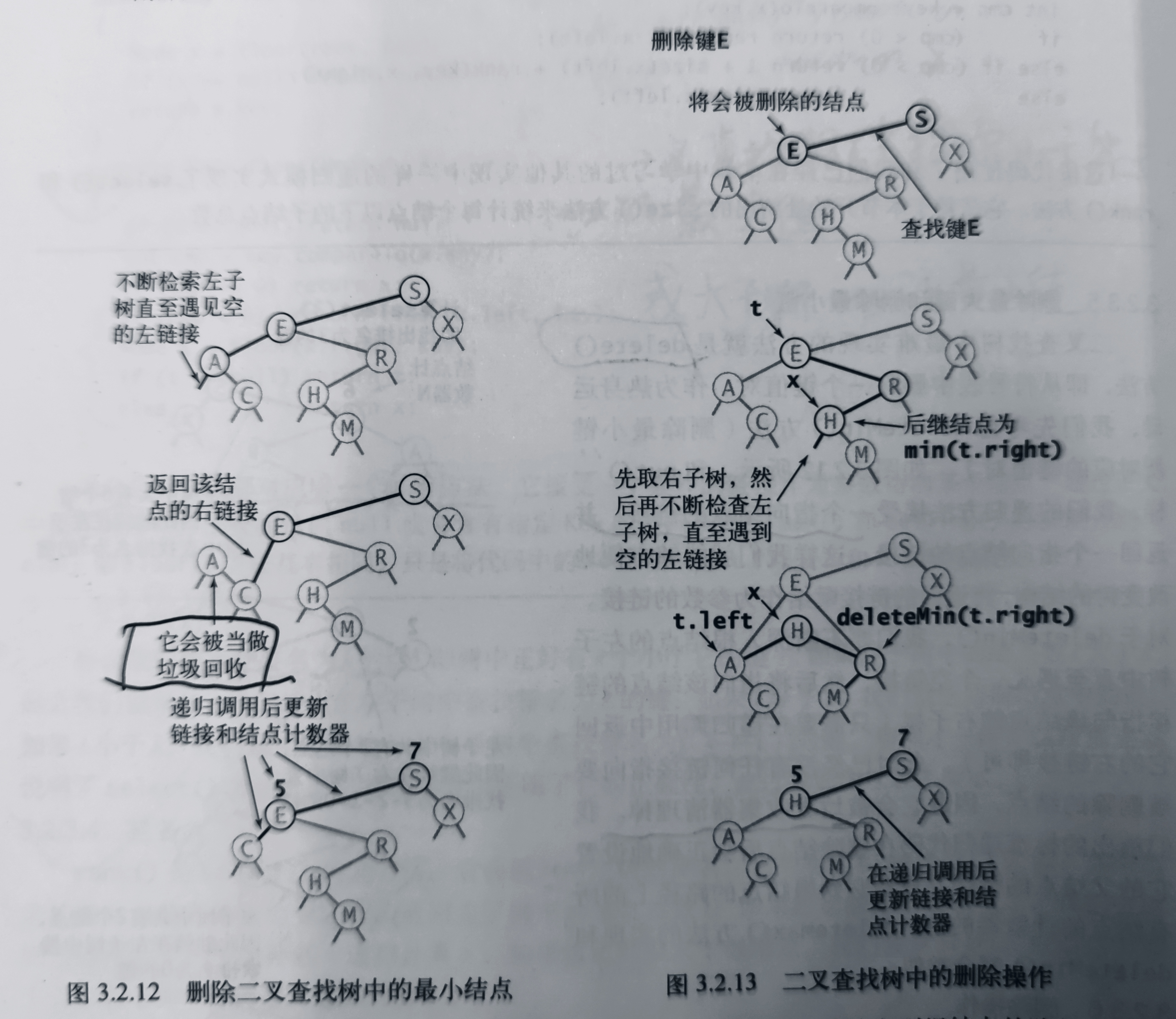
The code is as follows
/*** Delete minimum key***/
public void deleteMin() {
if (root == null) {
return;
}
deleteMin(root);
}
private Node deleteMin(Node x) {
if (x.left == null) {
return x.right;
}
x.left = deleteMin(x.left);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
🎈
Delete max key
The implementation of the deleteMax() method is completely similar to that of deleteMin(). Accordingly, you only need to delete the rightmost node of the right subtree, and then return to the left subtree of its rightmost node.
/*** Delete max key***/
public void deleteMax() {
if (root == null) {
return;
}
deleteMax(root);
}
private Node deleteMax(Node x) {
if (x.right == null) {
return x.left;
}
x.right = deleteMax(x.right);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
🎈
Delete operation
We can delete any node with only one child node (or no child node) in a similar way, but how to delete a node with two child nodes? After deletion, we have to deal with two subtrees, but the parent node of the deleted node has only one empty link. T.Hibbard put forward the first method to solve this problem in 1962. After deleting node x, use its successor node to fill its position. Because X has only one right child node, its successor node is the smallest node in its right subtree. Such replacement can still ensure the order of the tree, because there are no other keys between x.key and its successor nodes. We can complete the task of replacing x with its successor node in four simple steps (the specific process is shown in the figure below):
- Save the link to the node to be deleted as t;
- Point x to its successor node min(t.right);
- Point the right link of X (originally pointing to a binary search tree with all nodes greater than x.key) to deleteMin(t.right), that is, the sub binary search tree with all nodes still greater than x.key after deletion;
- Set the left link of x (originally empty) to t.left (all keys under it are smaller than the deleted node and its successor nodes).
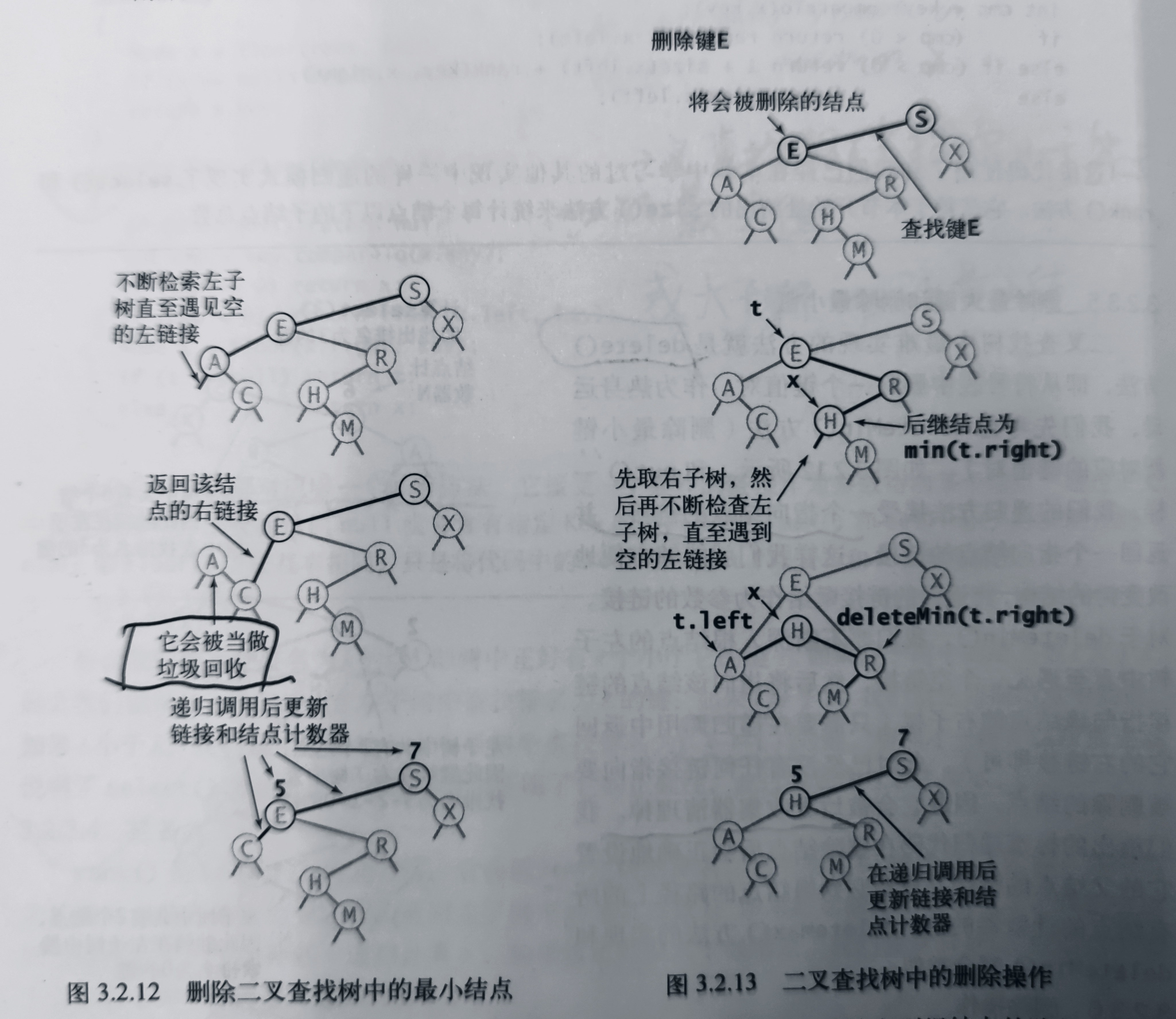
After the recursive call, we will correct the link of the parent node of the deleted node and reduce the counter of all nodes on the path from this node to the root node by 1 (here, the value of the counter will still be set to the total number of nodes in all its subtrees plus 1). Although this method can delete a node correctly, one of its shortcomings is that it may cause performance problems in some practical applications. The problem is that the selection of successor nodes is an arbitrary decision, and the symmetry of the tree is not considered. Can I use its precursor node? In fact, the choice of precursor node and successor node should be random.
/*** Delete operation***/
public void delete (Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
x.left = delete(x.left, key);
} else if(cmp > 0) {
x.right = delete(x.right, key);
} else {
if (x.right == null) {
return x.left;
}
if (x.left == null) {
return x.right;
}
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
}
performance analysis
Proposition: in a binary lookup tree, the time required for all operations in the worst case is directly proportional to the height of the tree.
Prove that all operations of the tree follow one or two paths of the tree. By definition, the length of the path cannot be greater than the height of the tree.
Q: I've seen binary lookup trees, but their implementation doesn't use recursion. What are the advantages and disadvantages of these two methods?
A: Generally speaking, recursive implementation is easier to verify its correctness, while non recursive implementation is more efficient.
Complete code and testing
🎈
Complete code
class BST<Key extends Comparable<Key>, Value> {
private Node root; //Root node of binary lookup tree
private class Node{
private Key key; //key
private Value val; //value
private Node left, right; //Link to subtree
private int N; //The total number of nodes in the subtree with this node as the root
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
public int size() {
return size(root);
}
private int size(Node x) {
if (x == null) {
return 0;
} else {
return x.N;
}
}
/*** Search***/
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {
//Find and return the value corresponding to the key in the subtree with x as the root node
//null if not found
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return get(x.left, key);
} else if (cmp > 0) {
return get(x.right, key);
} else {
return x.val;
}
}
/*** Insert***/
public void put(Key key, Value val) {
//Find the key and update its value if found. Otherwise, create a new node for it
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {
//If the key exists in the subtree with x as the root node, update its value;
//Otherwise, a new node with key and val as key value pairs will be inserted into the subtree
if (x == null) {
return new Node(key, val, 1);
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
x.left = put(x.left, key, val);
} else if (cmp > 0) {
x.right = put(x.right, key, val);
} else {
x.val = val;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
}
/*** Minimum key***/
public Key min() {
if (root == null) {
return null;
}
return min(root).key;
}
private Node min(Node x) {
if (x.left == null) {
return x;
}
return min(x.left);
}
/*** Maximum key***/
public Key max() {
if (root == null) {
return null;
}
return max(root).key;
}
private Node max(Node x) {
if (x.right == null) {
return x;
}
return max(x.right);
}
/*** Round down***/
public Key floor(Key key) {
Node x = floor(root, key);
if (x == null) {
return null;
}
return x.key;
}
private Node floor(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0) {
return x;
}
if (cmp < 0) {
return floor(x.left, key);
}
Node t = floor(x.right, key);
if (t != null) {
return t;
} else {
return x;
}
}
/**** Round up**/
public Key ceiling(Key key) {
Node x = ceiling(root, key);
if (x == null) {
return null;
}
return x.key;
}
private Node ceiling(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0) {
return x;
}
if (cmp > 0) {
return ceiling(x.right, key);
}
Node t = ceiling(x.left, key);
if (t != null) {
return t;
} else {
return x;
}
}
/*** Select operation (return key ranked k)***/
public Key select(int k) {
if (root == null) {
return null;
}
return select(root, k).key;
}
private Node select(Node x, int k) {
//Return the node ranked k
if (x == null) {
return null;
}
int t = size(x.left) + 1;
if (t > k) {
return select(x.left, k);
} else if (t < k) {
return select(x.right, k - t - 1);
} else {
return x;
}
}
/*** Returns the ranking of the given key***/
public int rank(Key key) {
if (root == null) {
return 0;
}
return rank(root, key);
}
private int rank(Node x, Key key) {
//Returns the number of keys smaller than x.key in the subtree with X as the root node
if (x == null) {
return 0;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return rank(x.left, key);
} else if (cmp > 0) {
return 1 + size(x.left) + rank(x.right, key);
} else {
return size(x.left) + 1;
}
}
/*** Range lookup (returns all key values within a given range)***/
public Iterable<Key> keys() {
return keys(min(), max());
}
public Iterable<Key> keys(Key lo, Key hi) {
Queue<Key> queue = new LinkedList<Key>();
keys(root, queue, lo, hi);
return queue;
}
private void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
if (x == null) {
return;
}
int cmplo = lo.compareTo(x.key);
int cmphi = hi.compareTo(x.key);
if (cmplo < 0) {
keys(x.left, queue, lo, hi);
}
if (cmplo <= 0 && cmphi >= 0) {
queue.offer(x.key);
}
if (cmphi > 0) {
keys(x.right, queue, lo, hi);
}
}
/*** Delete minimum key***/
public void deleteMin() {
if (root == null) {
return;
}
deleteMin(root);
}
private Node deleteMin(Node x) {
if (x.left == null) {
return x.right;
}
x.left = deleteMin(x.left);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
/*** Delete max key***/
public void deleteMax() {
if (root == null) {
return;
}
deleteMax(root);
}
private Node deleteMax(Node x) {
if (x.right == null) {
return x.left;
}
x.right = deleteMax(x.right);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
/*** Delete operation***/
public void delete (Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
x.left = delete(x.left, key);
} else if(cmp > 0) {
x.right = delete(x.right, key);
} else {
if (x.right == null) {
return x.left;
}
if (x.left == null) {
return x.right;
}
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
}
}
🎈
test
Build the tree in the order of the following key value pairs
int[] keys = {6, 5, 1, 3, 2, 4, 9, 7, 8, 10};
String[] values = {"F", "E", "A", "C", "B", "D", "I", "G", "H", "J"};
The binary lookup tree constructed is shown in the figure below
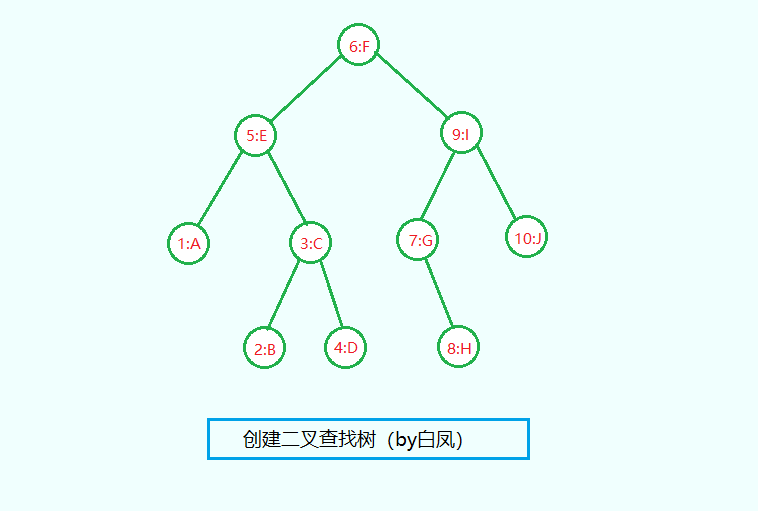
Relevant test codes are as follows
public class BSTTest {
public static void main(String[] args) {
int[] keys = {6, 5, 1, 3, 2, 4, 9, 7, 8, 10};
String[] values = {"F", "E", "A", "C", "B", "D", "I", "G", "H", "J"};
BST<Integer, String> bst = new BST<Integer, String>();
//Build tree
for (int i = 0; i < keys.length; i++) {
bst.put(keys[i], values[i]);
}
System.out.println("The key to create the tree is:");
LinkedList<Integer> queue = (LinkedList<Integer>) bst.keys();
while (!queue.isEmpty()) {
System.out.print(queue.poll() + " ");
}
System.out.println("\n The size of the created tree is:" + bst.size());
System.out.println("The value corresponding to key 3 is:" + bst.get(3));
System.out.println("The minimum key is:" + bst.min());
System.out.println("The maximum key is: " + bst.max());
System.out.println("The maximum keys less than or equal to 11 are:" + bst.floor(11));
System.out.println("The minimum key greater than or equal to 0 is: " + bst.ceiling(0));
System.out.println("The key ranked 5 is:" + bst.select(5));
System.out.println("The ranking of key 7 is:" + bst.rank(7));
System.out.println("\n The key value is 3-8 The keys between are:");
LinkedList<Integer> queue1 = (LinkedList<Integer>) bst.keys(3, 8);
while (!queue1.isEmpty()) {
System.out.print(queue1.poll() + " ");
}
System.out.println("\n The key values after deleting the minimum and maximum keys are:");
bst.deleteMin();
bst.deleteMax();
LinkedList<Integer> queue2 = (LinkedList<Integer>) bst.keys();
while (!queue2.isEmpty()) {
System.out.print(queue2.poll() + " ");
}
System.out.println("\n The key value after deleting key 4 is: ");
bst.delete(4);
LinkedList<Integer> queue3 = (LinkedList<Integer>) bst.keys();
while (!queue3.isEmpty()) {
System.out.print(queue3.poll() + " ");
}
}
}
The output results are as follows
The key to create the tree is: 1 2 3 4 5 6 7 8 9 10 The size of the created tree is: 10 The value corresponding to key 3 is: C The minimum key is: 1 The maximum key is: 10 The maximum key less than or equal to 11 is: 10 The minimum key greater than or equal to 0 is: 1 The key ranking 5 is: 5 The ranking of key 7 is: 7 The key value is 3-8 The keys between are: 3 4 5 6 7 8 The key values after deleting the minimum and maximum keys are: 2 3 4 5 6 7 8 9 The key value after deleting key 4 is: 2 3 5 6 7 8 9 Process finished with exit code 0
🎈
Reference: algorithm, Fourth Edition
Note: this blog is for learning and reference only. Please indicate the source of reprint (Baifeng, April 30, 2021)