Depth first search application
Example 1: alphabetical arrangement (subject library 2698)
Given a string composed of different lowercase letters, output all the full permutations of the string.
Let's assume 'a' < 'B' <... < 'for lowercase letters Y '<' Z ', and the letters in the given string have been arranged from small to large.
Input format
the input has multiple groups of data, one group per line. Each group of data is a string composed of lowercase letters. The length of the known string is between 1 and 6.
Output format
output all permutations of this string, one permutation per line. It is required that the ones with small alphabetical order should be arranged in the front. The dictionary order is defined as follows:
known S = s_1s_2...s_k , T = t_1t_2...t_kS=s1s2... sk,T=t1t2... tk, then "s < TS < T" is equivalent to the existence of "P (1 < = P < = k) P (1 < = P < = k), so that" s "_ 1 = t_ 1, s_ 2 = t_ 2, ..., s_ {p - 1} = t_ {p - 1}, s_ p < t_ ps1=t1,s2=t2,..., sp − 1 = tp − 1, sp < tp holds.
note that each group of sample output is followed by a blank line.
sample input
xyz
Copy
sample output
xyz xzy yxz yzx zxy zyx
Copy
Problem solving ideas: see code analysis for detailed problem solving ideas.
#include<bits/stdc++.h>
using namespace std;
char a[10];
int n,use[10];
string s;
void print()
{
for(int i=1;i<=n;i++)
{
cout<<a[i];
}
cout<<endl;
}
void dfs(int cur) //current location
{
if(cur>n) //Current position is greater than n, end
{
print(); //Output this arrangement
return;
}
for(int i=0;i<=n-1;i++) //Enumerates the value of the cur th element
{
if(use[i]==0) //i is not used by the previous element
{
a[cur]=s[i]; //Record element value
use[i]=1; //Mark i is used
dfs(cur+1); //Search for the value of the next element
use[i]=0; //After use, restore the state
}
}
}
int main()
{
while(cin>>s)
{
n=s.size();
dfs(1); //Row from the first position
cout<<endl;
}
return 0;
}
Copy
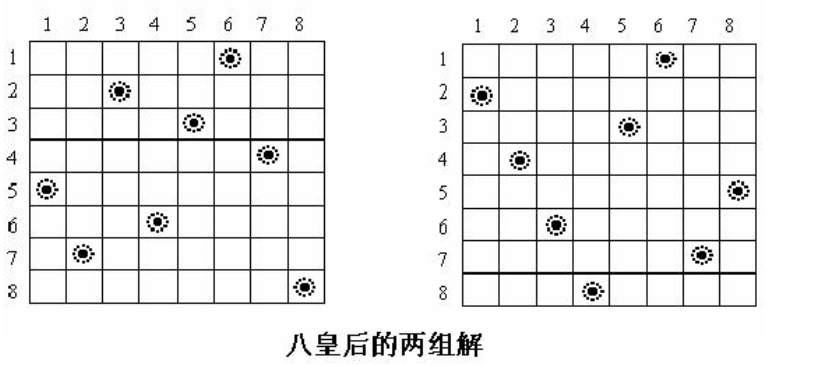
Example 2: Queen N problem (topic library 1285)
Put n queens in the chess board (the size of the board is n*n), so that any two Queens can't eat each other. (hint: the queen can eat any piece in the same row, column and diagonal.)
Input format: enter a line containing a positive integer n (n < = 8).
Output format: if there is a qualified placement method, output all solutions. Each solution occupies one line, in which each number occupies 5 characters wide and is aligned to the right; If there is no qualified solution, output "no solution!" (excluding quotation marks).
Sample input:
4
Copy
Sample output:
2 4 1 3 3 1 4 2
Copy
Example explanation:
As shown in the figure below, when n=4, there are two solutions for Queen placement:
Solution 1: 2 columns in the first row, 4 columns in the second row, 1 column in the third row and 3 columns in the fourth row. Together, it is 2 4 1 3
Solution 2: three columns in the first row, one column in the second row, four columns in the third row and one column in the fourth row. Together, it is 3 1 3 2
Problem solving ideas: see code analysis for detailed problem solving ideas.
#include<bits/stdc++.h>
using namespace std;
int a[10]; //Record the queen in row i in which column
int n,ans=0;
bool check(int row,int col){ //Judge whether the queen in row is placed in col
for(int i=1;i<row;i++) //I represents the row number, and a[i] represents the column number
{
if(a[i]==col||(abs(row-i)==abs(col-a[i]))) //If the column number already exists or is on the diagonal, the change value of the row is equal to the change value of the column
return false;
}
return true;
}
void dfs(int cur)
{
if(cur>n){ //Swing from top to bottom until the end of line n+1, that is, reach the destination
ans++; //Pendulum method++
for(int i=1;i<=n;i++) //Concrete pendulum method
{
cout<<setw(5)<<a[i]; //I represents the row number, a[i] represents the column number, and the output column number is the specific pendulum method
}
cout<<endl;
return; //void type function. Return without return value indicates the end of the function
}
for(int i=1;i<=n;i++) //If you do not get to row n+1, you need to place from one column to column n, and judge whether the column can be placed
{
if(check(cur,i)==true) //cur represents row and i represents column, indicating that the position can be placed
{
a[cur]=i; //The queen in row cur is placed in column i
dfs(cur+1); //Start searching for the next line
}
}
}
int main()
{
cin>>n;
dfs(1); //Start with the first line
if(ans==0)
cout<<"no solute!";
return 0;
}
Copy
Example 3: eight queens problem
Those who can play chess know that the queen can eat other pieces in unlimited steps on the horizontal, vertical and diagonal lines. How to put 8 queens on the chessboard (there are 8 Queens) × 8 squares), so that none of them can be eaten! This is the famous eight queens problem.
For the placement method of 8 queens that meet the requirements, define a queen string a corresponding to it, that is, a = b1b2 The number of places bi in row 8 is the corresponding number of places bi.
It is known that there are 92 sets of solutions (92 different queen strings) to the 8 queen problem.
Given a number B, it is required to output the b-th string. The comparison of strings is as follows: Queen string x is placed before queen string y, which is smaller than y if and only if x is regarded as an integer.
Input format: the first line is the number of test data groups n, followed by N lines. Each group of test data occupies one line, including a positive integer b(1 ≤ b ≤ 92).
Output format: there are n lines of output, and each line of output corresponds to one input. The output should be a positive integer, which is the queen string corresponding to b.
Input example 1:
2 1 92
Copy
Output example 1:
15863724 84136275
Copy
Problem solving ideas: see code analysis for detailed problem solving ideas.
#include<bits/stdc++. h>using namespace std; int res[100]; // Store each pendulum int n,t=0,a[100];bool check(int x,int y) / / check whether {for (int i = 1; I < x; I + +) {if (a [i] = = y|abs (X-i) = = ABS (a [i] - y)) / / horizontal, vertical and diagonal return false;} return true;} Int make() / / synthesize 1 5 8 6 3 7 2 4 into 15863724 {int x = 0; for (int i = 1; I < = 8; I + +) {x = x * 10 + a [i];} return x;} Void DFS (int cur) {if (cur > 8) / / don't write n. here is queen 8. If it exceeds 8, record {T + +; res [t] = make(); / / res [1] the first pendulum method, and so on... Return;} For (int i = 1; I < = 8; I + +) / / 8 lines {if(check(cur,i)==true) / / whether you can put {a[cur]=i; / / record the element value dfs(cur+1); / / search for the value of the next element}} int main() {int Q, m; DFS (1); CIN > > Q; / / sort (RES + 1, res + 1 + 92); / / you don't need to sort, which is already in order for (int i = 1; I < = q; I + +) {CIN > > m; cout < < res [M] < < endl; / / res [M] is the required}}
Copy
Example 4: Xiao Li goes to herd cattle
Finally, at the age of 60, Xiao Li made up his mind, left the city, came to rural life and lived an idyllic life (Xiao Li has grown into Lao Li)
Life in the countryside is very leisurely. Xiao Li also keeps an old yellow cow and often leads the old yellow cow to the pasture to eat grass. This cow has a unique ability to run and jump in the pasture like a horse in Chinese chess. Of course, the cow can't jump on rocks or trees, but it can jump where there is grass.
Here is a rectangular pasture with a width of X and a height of Y. Old yellow cattle like hay as much as other cattle. Now give you a map containing the starting place of the old yellow cattle and the location information of trees, rocks, shrubs or other obstacles and large bags of hay. Make sure that the old yellow cattle will jump a few "jumps" when they get hay. In the map, the starting place of the old cattle is represented by 'K'; Obstacles are represented by '*' and pasture by '.' The location of hay is indicated by 'H'. As shown below.
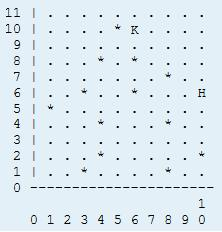
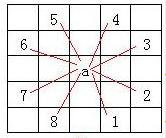
There are eight directions to explore in this rectangular pasture. The exploration sequence is in the sequence number in the figure below. Moreover, the old scalper's thinking is "one tendon". It will explore at each point according to the direction sequence in the figure, that is, if it can go in direction 1, it will go in direction 1. If it can't go or go, it will consider direction 2, and so on until it finds hay.
The steps of obtaining hay in the above figure are represented by a, B, C, D and E in the following figure, and 4 "jumps" are required (as shown below).
Input format:
Line 1, two spaces separated integers: X and Y.
Next, there are Y lines, each containing X characters without spaces, representing the map of this line.
Output format:
A row, a single integer, represents the number of "jumps" to find hay in this exploration order. Ensure that all data can get hay.
Sample
Enter #1
10 11..............*K.................*.*...........*....*..*...H*............*...*...............*.....*..*....*..
Copy
Output #1
4
Copy
Data scope / agreement
For 100% of the test data: 1 < = x < = 150, 1 < = y < = 1501 < = x < = 150, 1 < = y < = 150.
Problem solving ideas: see code analysis for detailed problem solving ideas
#include<bits/stdc++.h>
using namespace std;
char a[201][201]; //Map
int f[201][201]; //sign
int x,y; //Row x, column y
int bx,by,ex,ey; //Coordinates of start point and end point
int flag=0; //sign
int dx[8]={2,1,-1,-2,-2,-1,1,2}; //Search up and down
int dy[8]={1,2,2,1,-1,-2,-2,-1}; //Search left and right
bool check(int ix,int iy){ //judge
if(ix>=0&&ix<x&&iy>=0&&iy<y&&(a[ix][iy]=='.'||a[ix][iy]=='H'||a[ix][iy]=='K')){
return true; //If the current point is within the range (IX > = 0 IX < x iy > = 0 iy < y) and (currently at the starting point or end point or walkable point), return true (true(1))
}return false; //If one of the conditions is not met, false (false(0)) is returned;
}void dfs(int fx,int fy,int step){ //recursion
if(fx==ex&&fy==ey){ //recursion
flag=1; //Add a mark to end early
cout<<step; //output
return; //end
}for(int i=0;i<8;i++){ //Search deep search
if(check(fx,fy)&&f[fx][fy]==0&&flag==0){ //Judge whether the conditions are met
f[fx][fy]=1; //record
dfs(fx+dx[i],fy+dy[i],step+1); //recursion
f[fx][fy]=0; //record
}
}
}int main(){
cin>>y>>x; //Row x, column y
for(int i=0;i<x;i++){ //x line
for(int j=0;j<y;j++){ //y column
cin>>a[i][j]; //input
if(a[i][j]=='K'){ //Find a starting point
bx=i; //bx is the row coordinate of the starting point
by=j; //by is the column coordinate of the starting point
} //Find the starting point and mark it
if(a[i][j]=='H'){ //Find the end
ex=i; //ex is the row coordinate of the end point
ey=j; //ey is the column coordinate of the end point
} //Find the end point and mark it
}
}dfs(bx,by,0); //Deep search from the starting point
return 0; //Program end
}
Copy
Example 5: special prime ribs
Farmer John cows always produce the best ribs You can recognize them by the numbers on each rib marked by Farmer John and the U.S. Department of agriculture Farmer John determined that what he sold to the buyer was the real prime rib, because he cut the rib from the right, and the numbers on the remaining ribs each time form a prime number. For example:
7 3 3 1
The number 7331 on all ribs is a prime number; Three ribs 733 are prime numbers; The two ribs 73 are prime numbers; Of course, the last rib 7 is also a prime number. 7331 is called a special prime number of length 4
Write a program to find all special prime numbers for a given number of ribs n (1 < = n < = 8) The number 1 is not considered a prime number
Input format: one line, one integer N
Output format: multiple lines, output special prime numbers with length N in sequence, one for each line
Input example 1:
4
Copy
Output example 1:
2333 2339 2393 2399 2939 3119 3137 3733 3739 3793 3797 5939 7193 7331 7333 7393
Copy
Problem solving ideas: see code analysis for detailed problem solving ideas.
#include<bits/stdc++.h>
using namespace std;
int n;
bool prime(int x){ //Prime judgment
if(x==1) return 0;
else{
for(int i=2;i<=sqrt(x);i++)
{
if(x%i==0) return 0;
}
return 1;
}
}
void dfs(int cur,int sum) //What is the current number and the value of this number
{
for(int i=1;i<=9;i++) //1 to 9 per location
{
if(prime(sum*10+i)==1) //Judge whether this number is a prime number
{
if(cur==n) cout<<sum*10+i<<endl; //If it is exactly the nth number, output this number
else dfs(cur+1,sum*10+i); //Start searching for the next number
}
}
}
int main()
{
cin>>n;
dfs(1,0); //For the first number, the starting value of sum is 0
return 0;
}
Copy
Example 6: arrangement of set elements
Solution 1:
#include<bits/stdc++.h>
using namespace std;
int n,r,a[110],f[110],b[110],c;
void dfs(int step)
{
if(step==r+1)
{
for(int i=1;i<=r;i++)
{
cout<<setw(3)<<a[i];
}
cout<<endl;
return ;
}
for(int i=1;i<=n;i++)
{
if(f[i]==0&&i>a[step-1])
{
f[i]=1;
a[step]=i;
dfs(step+1);
f[i]=0;
}
}
return ;
}
int main()
{
cin>>n>>r;
dfs(1);
}
Copy
Solution 2:
#include <bits/stdc++.h>
using namespace std;
int flag[101];
int n, r;
void dfs(int x, int k)
{
// Boundary return condition: processing of current node
if(k == r)
{
for(int i = 1; i <= n; i++)
if(flag[i])
cout << setw(3) << i;
cout << endl;
return;
}
// Keep looking for the next number
for(int i = x+1; i <= n; i++)
{
flag[i] = 1; // Select i
dfs(i, k+1);
flag[i] = 0; // Deselect
}
}
int main()
{
cin >> n >> r;
dfs(0, 0);
return 0;
}
Copy
Example 7: number of choices
Solution 1:
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=30;
int a[N],cnt,s[N];
bool f[N];
bool ss(int k){
if(k<2) return false;
for(int i=2;i<=sqrt(k);i++)
if(k%i==0)
return false;
return true;
}
void dfs(int t,int c){
int sum=0;
if(t==m+1){
for(int i=1;i<=m;i++){
sum+=s[i];
}
if(ss(sum)==true)
cnt++;
return;
}
for(int i=c+1;i<=n;i++){
if(f[i]==0){
s[t]=a[i];
f[i]=1;
dfs(t+1,i);
f[i]=0;
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
dfs(1,0);
cout<<cnt;
return 0;
}
Copy
Solution 2:
#include<bits/stdc++.h>
using namespace std;
int ans;
int n,k;
int x[21];
bool prime(int n)
{
if(n<=1) return false;
for(int i=2;i<=n-1;i++)
{
if(n%i==0)
return false;
}
return true;
}
void dfs(int p,int s,int sum) // p: Currently selected position s: number of currently selected digits sum: current digits and
{
if(s==k)
{
if(prime(sum)) ans++;
return;
}
for(int i=p+1;i<=n;i++)
{
dfs(i,s+1,sum+x[i]);
}
}
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
cin>>x[i];
dfs(0,0,0);
cout<<ans;
return 0;
}
Copy
Example 8: splitting natural numbers
"When the world is bustling, all benefits come; when the world is bustling, all benefits go". The purpose of the dark forces in the prison to divide the territory is nothing more than to obtain benefits. Their way of distributing benefits is based on such a criterion: if the total benefit is the natural number n, any n greater than 1 can always be divided into the sum of several natural numbers less than n, After finding all the splits of N, select the most appropriate one for allocation. For example, when N=3, there are two kinds of divisions, namely 3 = 1 + 2 and 3 = 1 + 1 + 1. Try to find all the splits of n.
Input format: an integer, i.e. N, N ≤ 45.
Output format: output each division scheme, each division scheme occupies one line, and the last line is the total number of schemes.
Input example 1:
3
Copy
Output example 1:
3=1+2 3=1+1+1 2
Copy
Note: you can ignore the output order of the division scheme. The system supports wrong line comparison.
Solution idea: Problem Description: select some numbers and make their sum n. The optional range of each number is [1, n-1]
A single number can be used repeatedly, for example: 3 = 1 + 1 + 1, but it cannot be repeated. For example, 1 + 2 and 2 + 1 are the same solution. The optional range of the cur element is: [a[cur-1],n-1]
The number of elements in the solution is uncertain. When the sum of elements is n, it reaches the destination.
Pruning function: for values, if the sum of the selected elements is sum + i > N, i is not optional.
The complete code is as follows:
#include<bits/stdc++.h>
using namespace std;
const int N=50;
int n,a[N],ans;
void print(int cur)
{
ans++;
cout<<n<<"="<<a[1];
for(int i=2;i<cur;i++)
{
cout<<"+"<<a[i];
}
cout<<endl;
}
void dfs(int cur,int sum)
{
if(sum==n) //terminus ad quem
{
print(cur);
return;
}
for(int i=a[cur-1];i<n;i++) //Optional range of the cur th element;
{
if(sum+i<=n) //prune
{
a[cur]=i;
dfs(cur+1,sum+i);
}
}
}
int main()
{
cin>>n;
a[0]=1;
dfs(1,0);
cout<<ans;
return 0;
}
Copy
Example 9: sum is zero (topic library 2662)
Consider an increasing sequence of numbers from 1 to n (N=9): 1, 2, 3 N. Now please insert "+" to add, or "-" to subtract, or "" to space (for example, 1, 2, 4 is equivalent to 124) in the sequence to combine each pair of numbers (please do not insert a symbol before the first number) Evaluate the result of the expression and judge whether its value is 0. Please write a program to find all the sequences with length n whose sum is zero.
Input format: a single line represents integer n (3 < = n < = 9)
Output format: according to the order of ASCII code, output all the series whose sum is zero after inserting "+", "-", or "" between each pair of numbers (Note: spaces should be left even if there is no caret between two numbers)
Input example 1:
7
Copy
Output example 1:
1+2-3+4-5-6+7 1+2-3-4+5+6-7 1-2 3+4+5+6+7 1-2 3-4 5+6 7 1-2+3+4-5+6-7 1-2-3-4-5+6+7
Copy
Problem solving ideas: see code analysis for detailed problem solving ideas.
#include <iostream>
using namespace std;
const int N = 20;
const char X[3] = {' ', '+', '-'}; // ascii code '<' + '<' - '
int n;
char ans[N];
void print(){
for(int i=1; i<n; i++) //n-1 before cycle
{
cout << i << ans[i]; //Output number plus sign
}
cout << n << endl; //Output the last number
}
//Evaluate the value of the expression.
int check(){ //Focus on how to calculate the value of 0, especially in the case of spaces
int sum = 0, num = 1; //It is understandable that the default first operator must be 0 + 1
char lastop = '+'; //The front of + '1 is OK
for(int i=1; i<n; i++) {
if(ans[i] == ' ') //If the symbol is a space
num = num * 10 + (i + 1); //For example, 2 3 should be 2 * 10 + 3 = 23
else {
if(lastop == '+') sum += num; //If it's not a space, add or subtract directly
else sum -= num;
num = i+1; lastop = ans[i]; //Here, the values of num and lastop need to be updated, which is very important
}
}
if(lastop == '+') sum += num; //Judge the last number
else sum -= num;
return sum;
}
//Search for n-1 locations, each with '+', '-' or '
//cur indicates the location number currently searched [1, n-1].
void dfs(int cur){ //Full permutation problem, enter the current position
if(cur > n-1 ) { //End over n-1
if(check() == 0) print(); //If the value of the check formula is 0, it will be output
return;
}
for(int i=0; i<=2; i++) { //Traverse three symbols
ans[cur] = X[i]; //The ans array stores symbols
dfs(cur + 1); //Search next
}
}
int main() {
cin >> n; //If n=7, there are n-1=6 voids
//0 + 1
dfs(1); //Start the search at an interval between 1 and 2.
return 0;
}
Copy
Example 10: work assignment
#include<bits/stdc++.h>
using namespace std;
int minn=99999999999,ans;
int a[1001][1001],b[1001];
int n;
void dfs(int step)
{
if(step==n+1)
{
minn=min(ans,minn);
return ;
}
for(int i=1;i<=n;i++)
{
if(b[i]==0&&ans<minn)
{
b[i]=1;
ans+=a[step][i];
dfs(step+1);
ans-=a[step][i];
b[i]=0;
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
}
}
dfs(1);
cout<<minn;
}
Copy
Example 11: combined data retrieval
#include<bits/stdc++.h>
using namespace std;
int n,k,a[10010],f[10010],ans,mx,ok;
int p(int x)
{
if(x==1||x==0) return 0;
for(int i=2;i<=sqrt(x);i++)
{
if(x%i==0) return 0;
}
return 1;
}
void dfs(int d,int c,int s)
{
if(c==k+1)
{
if(ok) s=mx-s;
if(p(s)) ans++;
return;
}
for(int i=d+1;i<=n;i++)
{
dfs(i,c+1,s+a[i]);
}
}
int main()
{
cin>>n>>k;
if(k>n-k)
{
k=n-k;
ok=1;
}
for(int i=1;i<=n;i++)
{
cin>>a[i];
mx+=a[i];
}
dfs(0,1,0);
cout<<ans;
return 0;
}
Copy
Example 12: maze problem
#include <bits/stdc++.h>
using namespace std;
int n, a[12][12];
bool f[12][12];//Tag array
int ans = 0;
int dx[8] = {0,0,1,1,1,-1,-1,-1};//x direction
int dy[8] = {-1,1,0,1,-1,0,1,-1};//y direction
void dfs(int x, int y)
{
if(x == 1 && y == n){
ans ++;
return ;
}
if(x <= 0 || y <= 0 || x > n || y > n || a[x][y] == 1 || f[x][y] == 1)
return;
for(int i = 0; i < 8; i++)
{
f[x][y] = 1;//Mark as accessed
dfs(x + dx[i], y + dy[i]);
f[x][y] = 0;//Unmark
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
cin >> a[i][j];
}
}
dfs(1, 1);
cout << ans;
}
Copy
Example 13: optimal scheduling problem
#include<bits/stdc++.h>
using namespace std;
int n,k,ans=0xffffff,a[1001],s[1001];
int cmp(int a,int b)
{
return a>b;
}
void dfs(int x,int y)
{
int i;
if(ans<=y)
return;
if (x==n+1)
{
if(ans>y)
ans=y;
return;
}
for(i=1;i<=k;++i)
{
if(s[i]+a[x]<ans)
{
s[i]+=a[x];
dfs(x+1,max(y,s[i]));
s[i]-=a[x];
}
}
return;
}
int main()
{
int i;
cin>>n>>k;
for(i=1;i<=n;++i)
{
cin>>a[i];
}
sort(1+a,a+1+n,cmp);
dfs(1,0);
cout<<ans;
return 0;
}
Copy
Example 14: healthy Holstein cows
Farmer John is proud to have the healthiest cows in the world. He knows the amount of vitamins in each feed and the minimum daily vitamin requirements of dairy cows. Please help the farmer feed his cattle to keep them healthy and minimize the amount of feed fed to the cattle.
Give the minimum amount of vitamin required by cattle, output what kind of feed is needed for cattle, and the minimum amount of feed is required. The amount of vitamins is measured in integer units. Each feed can only be used for cattle once at most. The data ensure that there is a solution.
Input format:
Line 1: an integer V (1 < = V < = 25), indicating the number of vitamins required
Line 2: V integers (1 < = each number < = 1000), indicating the minimum amount of each vitamin needed by cattle every day
Line 3: an integer g (1 < = g < = 15), indicating the number of feeds available for cattle.
The next line G, line i, indicates the amount of various vitamins contained in the feed numbered i
Output format: the output file has only one line, including the minimum number of feed species P necessary for cattle. There are p numbers after it, indicating the selected feed number (arranged from small to large). If there are multiple solutions, the output feed has the smallest sequence number (i.e. the smallest dictionary order).
Input example 1:
4 100 200 300 400 3 50 50 50 50 200 300 200 300 900 150 389 399
Copy
Output example 1:
2 1 3
Copy
Problem solving ideas:
Define the problem and the solution to the problem: select some from G kinds of feed and ask them to contain vitamins to meet the daily needs of cattle.
Permutation problem or subset problem? Answer: select a subset satisfying certain properties from set G, and the solution space is a subset tree;
Arrive at the destination: all G feeds have been selected (choose or not) >
Optional set: there are two options for each feed: choose or not.
Pruning: if the number of selected feeds is > = the best scheme searched after adding the ith feed, pruning is required.
The complete code is as follows:
#include <iostream>
using namespace std;
const int MAXV = 30;
const int MAXF = 20;
//Subset problem, select a part from G kinds of feed to meet the daily feed needs of cattle
int numv, req[MAXV]; //Types and requirements of vitamins.
int numf, feeds[MAXF][MAXV]; //The amount of feed and the vitamins contained in each feed.
int best = MAXF+1; //The best feed type;
bool curf[MAXF], bestf[MAXF]; //The currently selected feed number and the best selected feed number.
//Whether it meets the demand of cattle for vitamins)
bool is_ok(){
for(int i=1; i<=numv; i++)
if(req[i] > 0) return false;
return true;
}
// Bit vector method
// cur indicates the current feed number
// num represents the currently selected feed type
void dfs(int cur, int num)
{
if(cur > numf) { //terminus ad quem.
if(is_ok()) { //Whether it meets the conditions.
best = num;
for(int i=1; i<=numf; i++)
bestf[i] = curf[i];
}
return;
}
if(num + 1 < best){//Whether the conditions are met (pruning)
//Save results
curf[cur] = true;
for(int j=1; j<=numv; j++)
req[j] -= feeds[cur][j];
dfs(cur+1, num+1); //Try the next feed
//Restore state
for(int j=1; j<=numv; j++)
req[j] += feeds[cur][j];
}
//No choice
curf[cur] = false;
dfs(cur+1, num);
}
int main()
{
cin >> numv; //Amount of vitamins needed by cattle
for(int i=1; i<=numv; i++) cin >> req[i];
cin >> numf; //Feed type
for(int i=1; i<=numf; i++)
for(int j=1; j<=numv; j++)
cin >> feeds[i][j];
dfs(1, 0); //Start with the first feed.
cout << best << " ";
for(int i=1; i<=numf; i++)
if(bestf[i]) cout << i << " ";
return 0;
}
Copy
Example 15: chessboard problem (topic library 1620)
There is a {m × mm × m ¢ chessboard. Each grid on the chessboard may be red, yellow or without any color. Now you have to go from the top left corner of the chessboard to the bottom right corner of the chessboard.
At any moment, the position you stand in must be colored (not colorless), and you can only move up, down, left and right. When you move from one grid to another, if the colors of the two grids are the same, you don't need to spend gold coins; If it is different, you need to spend 1 gold coin.
In addition, you can spend 2 gold coins to cast magic to temporarily change the next colorless grid to the color you specify. But this magic can't be used continuously, and the duration of this magic is very short. That is to say, if you use this magic and go to this temporarily colored grid, you can't continue to use magic; You can only continue to use this magic when you leave this position and go to a colored grid. When you leave this position (cast magic to make it a colored grid), the grid returns to colorless.
Now you have to go from the top left corner of the chessboard to the bottom right corner of the chessboard. What is the minimum gold coin to spend?
Input format: the input file name is chess in.
The first row of data contains two positive integers, m, nm and n, separated by a space, representing the size of the chessboard and the number of colored grids on the chessboard.
The next ^ nn ^ line has three positive integers ^ x, y, cx, y and c in each line, which respectively represent the color ^ cc of the grid with coordinates (x, y)(x, y). Where c=1c=1 , represents yellow and c=0c=0 , represents red. Two adjacent numbers are separated by a space. The coordinates of the upper left corner of the chessboard are (1,1) (1,1), and the coordinates of the lower right corner are (m, m)(m,m).
The rest of the squares on the chessboard are colorless. Ensure that the upper left corner of the chessboard, that is, (1,1) (1,1) must be colored.
Output format: the output file name is chess out.
Output a line and an integer, indicating the minimum value of gold coins spent. If it cannot be reached, output - 1 − 1.
Sample
Enter #1
5 7 1 1 0 1 2 0 2 2 1 3 3 1 3 4 0 4 4 1 5 5 0
Copy
Output 1
8
Copy
Interpretation 1
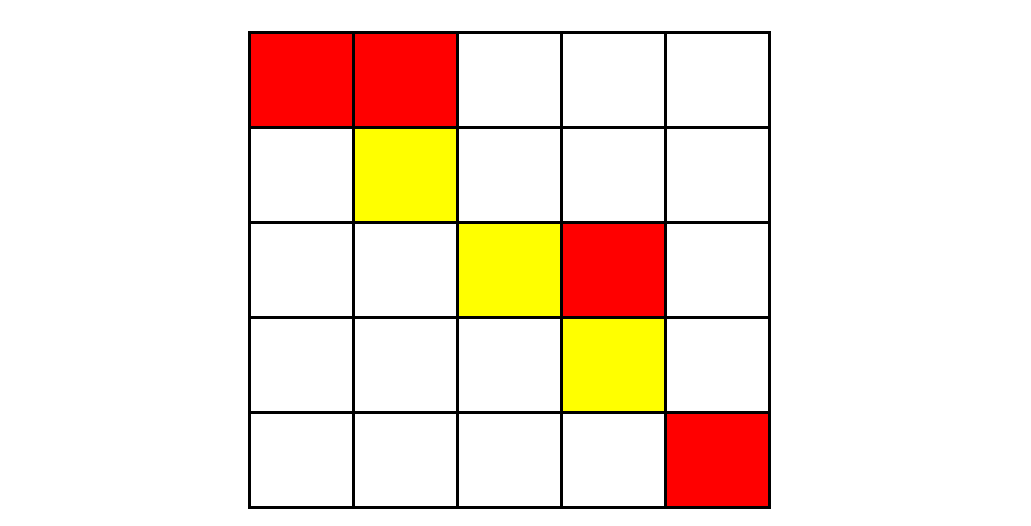
Start with (1, 1) and go to (1, 2) without spending gold coins
Go down from (1, 2) to (2, 2) and spend 1 gold coin
Cast magic from (2, 2), change (2, 3) to yellow, cost 2 gold coins
It costs no gold coins to walk from (2, 2) to (2, 3)
It costs no gold coins to walk from (2, 3) to (3, 3)
It costs 1 gold coin to walk from (3, 3) to (3, 4)
It costs 1 gold coin to walk from (3, 4) to (4, 4)
Cast magic from (4, 4), turn (4, 5) into yellow, and cost 2 gold coins,
It costs no gold coins to walk from (4, 4) to (4, 5)
It costs 1 gold coin to walk from (4, 5) to (5, 5)
A total of 8 gold coins were spent.
Input 2
5 5 1 1 0 1 2 0 2 2 1 3 3 1 5 5 0
Copy
Output 1
-1
Copy
Interpretation 1
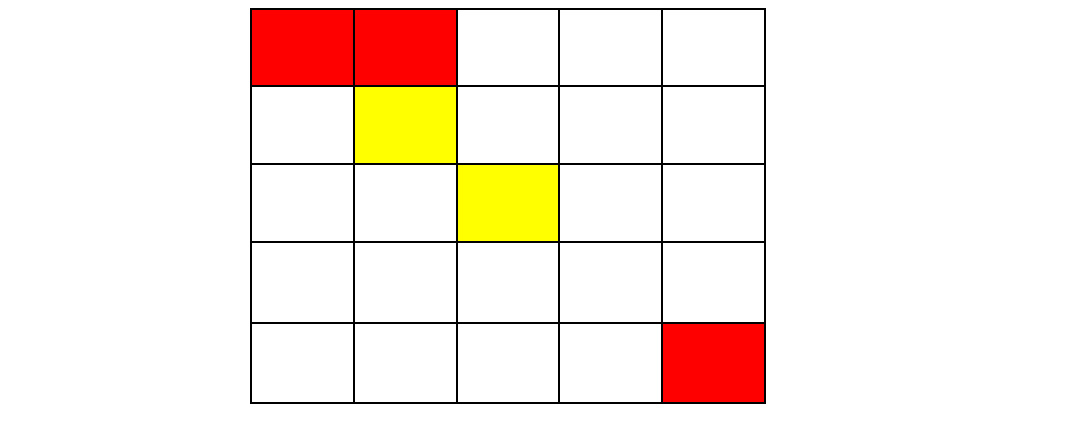
From (1, 1) to (1, 2), it doesn't cost gold coins
It costs 1 gold coin to walk from (1, 2) to (2, 2)
Cast magic to turn (2, 3) into yellow and spend 2 gold coins from (2, 2) to (2, 3)
It costs no gold coins to walk from (2, 3) to (3, 3)
From (3, 3), you can only cast magic to (3, 2), (2, 3), (3, 4), (4, 3)
However, it is impossible to reach (5, 5) from the above four points, so it is impossible to reach the end point, output - 1.
Data scope / agreement
Time and space limit: 1s, 256MB
For 30% of data, 1 ≤ m ≤ 5, 1 ≤ n ≤ 101 ≤ m ≤ 5, 1 ≤ n ≤ 10.
For 60% of the data, 1 ≤ m ≤ 20, 1 ≤ n ≤ 2001 ≤ m ≤ 20, 1 ≤ n ≤ 200.
For 100% data, 1 ≤ m ≤ 100, 1 ≤ n ≤ 10001 ≤ m ≤ 100, 1 ≤ n ≤ 1000.
Problem solving idea: define the solution of the problem: a path from (1,1) to (m, m) constitutes a solution of the problem, and the solution with the least cost is the answer of the problem.
Arrive at the destination: arrive at (m, m), that is, arrive at the destination.
Optional range: you can search up, down, left and right in the search process. According to the cost of gold coins, it can be divided into four cases:
① The color of the grid you go to is the same as that of the current grid. It costs 0 gold coins. ② The color of the grid you go to is different from the current grid. It costs 1 gold coin. ③ The square you go to has no color. The current square has color. It costs 2 gold coins. ④ The grid you are going to has no color. The current grid has no color and is not passable.
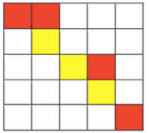
During the search process, multiple paths will reach the same location, as shown in the figure below, from (1, 1) to (2, 2)
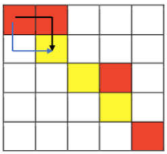
Both black path and blue path can reach (2, 2) from (1, 1), and there are as many paths to reach (m, m) from (2, 2).
The cost of black path to (2,2) is: 0 + 1 = 1, and the cost of blue path to (2,2) is 2 + 1 = 3.
The cost of arriving at (2,2) by the black path is less than that by the blue path. After arriving at (2,2), there is no need to continue searching.
Memory search: record the lowest cost of reaching any position (x, y) from (1, 1) during the search process. If the cost of reaching (x, y) again on a certain path is higher than the lowest cost that has been searched, prune.
The complete code is as follows:
#include<bits/stdc++.h>
using namespace std;
//Goal: use the minimum cost to go from (1,1) to (m,n)
//All the grids that have arrived must be colored (if there is no color at first, it must have been changed by now)
const int M=105,INF=2*M*M,dlt[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
//c[i][j] record the color of grid (i,j), 0-colorless, 1-red, 2-yellow
//d[i][j] record the minimum cost from the starting point to the grid (i,j)
int m,n,c[M][M],d[M][M];
inline bool legal(int x,int y)
{
return x>=1&&x<=m&&y>=1&&y<=m;
}
//x. Y represents the coordinates of the lattice
//x. Y represents the current color of the grid (x,y)
//color indicates the cost of lattice (x,y)
void dfs(int x,int y,int color,int cost)
{
if(cost>=d[x][y]) return;
d[x][y]=cost;
for(int i=0;i<4;i++)
{
int dx=x+dlt[i][0],dy=y+dlt[i][1]; //Coordinates of the next position
if(legal(dx,dy)){
if(c[dx][dy]==color)
dfs(dx,dy,color,cost); //The same color costs no money
else if(c[dx][dy]) dfs(dx,dy,c[dx][dy],cost+1); //There are colors and the colors are different
//③ (dx,dy) is colorless. At this time, (x,y) must have an initial color to continue
else if(c[x][y]) dfs(dx,dy,color,cost+2);
}
}
}
int main()
{
cin>>m>>n;
int x,y,z;
for(int i=1;i<=n;i++)
{
cin>>x>>y>>z;
c[x][y]=z+1; //Record the color of the colored grid
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
d[i][j]=INF; //Initialize to maximum
}
}
//Search from (1,1)
dfs(1,1,c[1][1],0);
if(d[m][n]!=INF) cout<<d[m][n];
else cout<<-1;
return 0;
}
Copy