I summary
Quick sort is an improvement of bubble sort.
Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.

II principle
1. First, set a boundary value (the default is the first number), and divide the array into left and right parts through the boundary value;
2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;
3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.
4. By repeating the above process, it can be seen that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed.

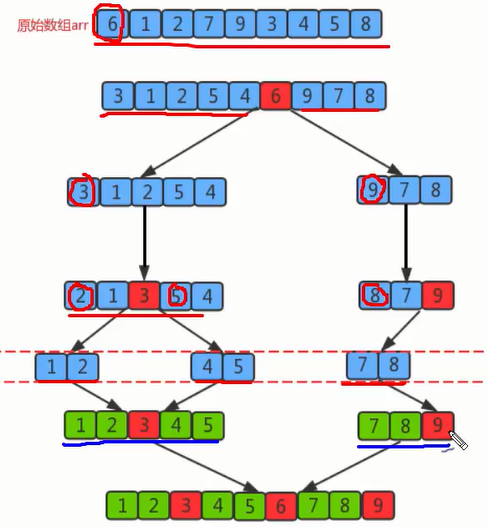
Specific segmentation process:
1. Find a reference value (the default is the first element), and point to the head and tail of the array with two pointers respectively;
2. Search for an element smaller than the reference value from right to left, stop when the search is reached, and record the position of the pointer;
3. Search for an element larger than the reference value from left to right, stop when it is found, and record the position of the pointer;
4. Exchange the elements of the current left pointer position and the right pointer position;
5. Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer.

Example:
Set the reference value and prepare two pointers. The left pointer points to the index lo where the boundary value is located, and the right pointer points to hi+1.
Idea: the right pointer goes from right to left to find elements smaller than 6; Then left, go from left to right, find elements larger than 6 (two-way investigation), and then exchange two numbers.

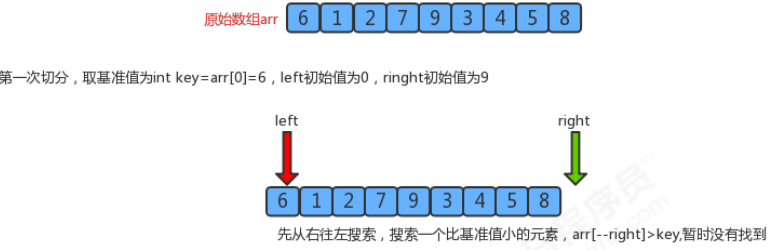
For the first time, the right pointer moves one bit to the left and points to 8, 8 > 6, which is not satisfied. Move left again to 5, 5 < 6, satisfied, the pointer pauses at 5.
Similarly, the left pointer moves to the right to find elements larger than 6. Moving to 1 and 2 in turn is not satisfied until it points to 7, 7 > 6.

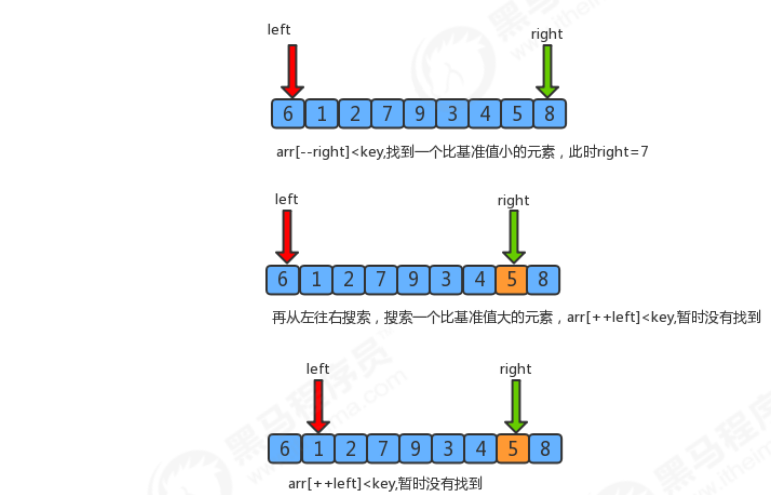
Swap "5" pointed to by the right pointer and "7" pointed to by the left pointer.

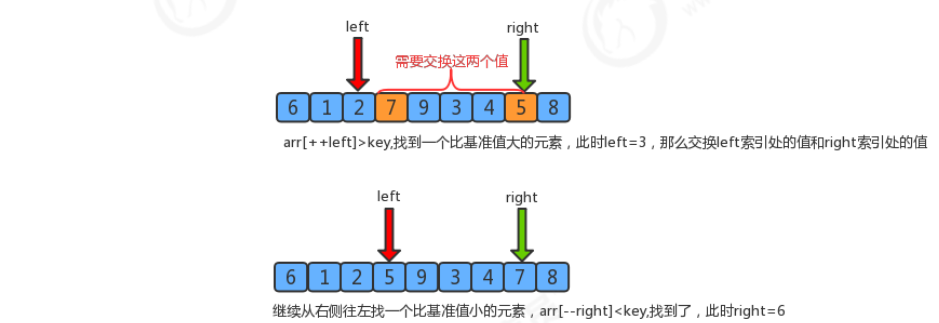
After exchanging the elements pointed to by the two pointers, the right pointer continues to move left to find 4 < 6, then left to find 9 > 6, and exchange 4 and 9.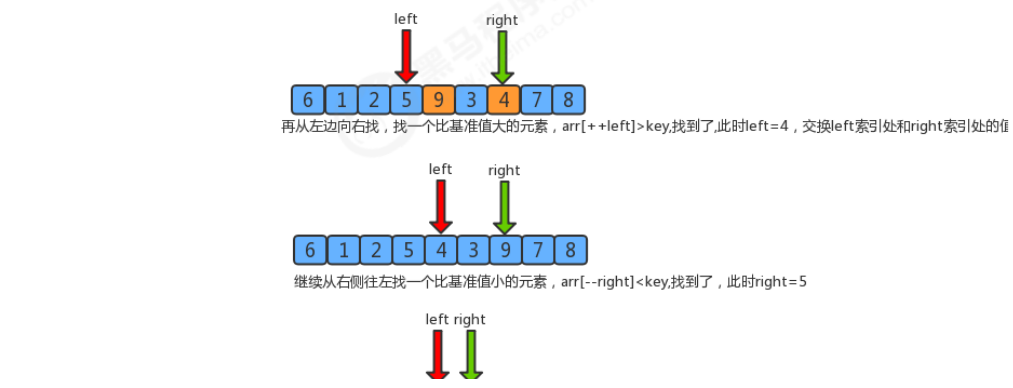Again, the right pointer moves left, finds 3 < 6, and the pointer stops at 3. The left pointer moves to the right to 3, that is, the position of the right pointer. At this time, the conditions are met (left > = right). The left and right pointers coincide, that is, it means that the two pointers have been scanned. At this time, the boundary value 6 and the value 3 pointed by the two pointers are exchanged.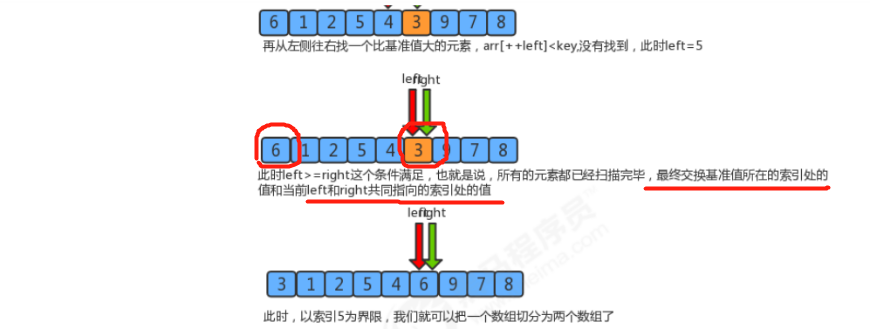
The segmentation of this array is completed, and then it is divided into two arrays with the boundary value as the boundary, and then repeat the above steps.

III Java code implementation

public class quick {
    public static void sort(int[] a){
        int lo=0;
        int hi=a.length-1;
        sort(a,lo,hi);

    }

    public static void sort(int[]a,int lo,int hi){
    if(lo>=hi){//Security check, i.e. recursive exit
        return;
    }
        int partition=partition(a,lo,hi); //Return the index after boundary value exchange (the last right value)
        //Continue recursive segmentation according to the boundary value
        sort(a,lo,partition-1);
        sort(a,partition+1,hi);
    }

    private static int partition(int[] a, int lo, int hi) {
        //Determine boundary value
        int key=a[lo];
        //Define two pointers to the next bit at the minimum index and the maximum index of the segmented array
        int left=lo;
        int right=hi+1;
        //segmentation
        while(true) {
            //First right
            while (a[--right]>key) {//Right < key is found, and the cycle condition is opposite.
                if(right==lo){
                    break;}
                }
            //Rear left
            while(a[++left]<key){ //Left > key is found, and the cycle condition is opposite
                if(left==hi){
                    break;
                }
            }
            //The left and right pointers coincide, that is, the troubleshooting is completed and the outermost cycle is jumped out
            if(left>=right){
                break;
            }else{
                swap(a,left,right);//If the pointers do not coincide, the elements at the left and right pointers are exchanged
            }
        }
        swap(a,lo,right);//Finally, the boundary values and coincidence elements are exchanged
        return right;//Returns the index after boundary value exchange
    }

    public static void swap(int[] a,int lo,int hi){
     int k=a[lo];
     a[lo]=a[hi];
     a[hi]=k;
    }
    
    public static void main(String[] args) {
        int[]a={6, 1, 2, 7, 9, 3, 4, 5, 8};
        sort(a);
        System.out.println(Arrays.toString(a));
    }
}

Operation results:

[1, 2, 3, 4, 5, 6, 7, 8, 9]