AES encryption principle
brief introduction
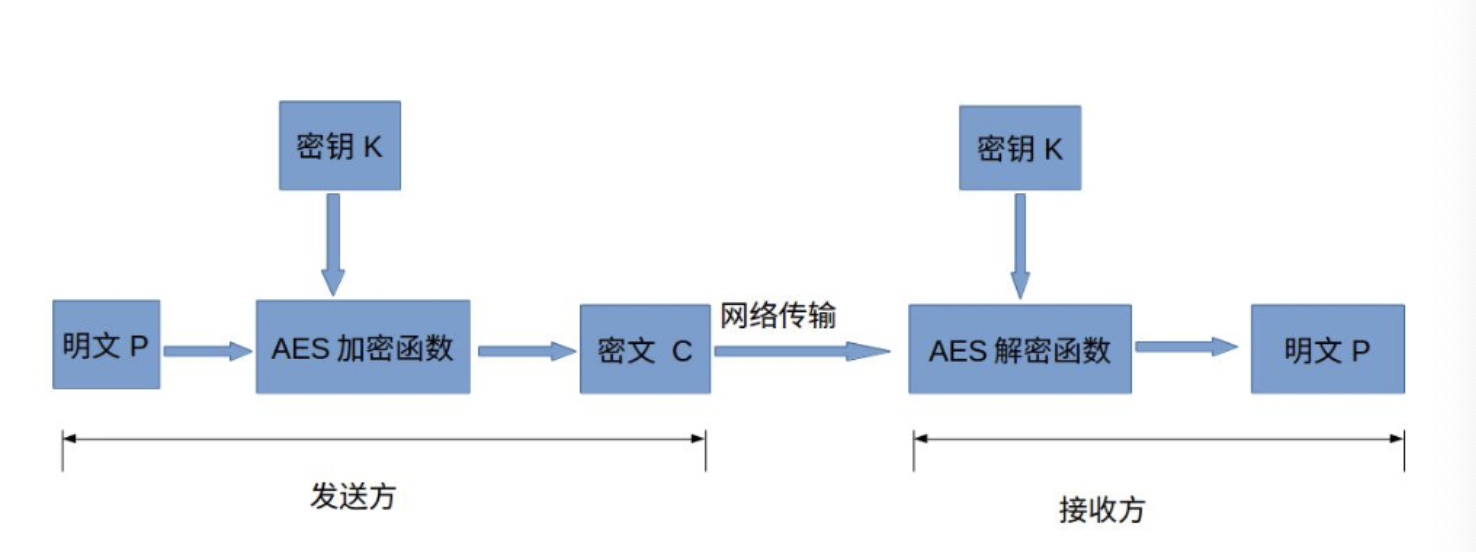
Advanced Encryption Standard (AES), also known as Rijndael encryption method, is a block encryption standard adopted by the federal government of the United States. It is also an alternative to DES algorithm and one of the most popular symmetric encryption algorithms today. Symmetric encryption is to use the same key when encrypting and decrypting data.
To learn AES algorithm, we must first understand the basic concepts of AES: key, filling mode, encryption mode and so on.
scene
Suppose one party wants the receiver to send a message. If the content is not encrypted, the sender wants the receiver to send a clear text message "is Xiao Ming there?". This message may be spied by the middleman to expose the contents of both sides of the communication. Therefore, we cannot transmit plaintext and must encrypt it. Both parties transmit ciphertext by using symmetric encryption.

Basic structure of AES
AES is block cipher. Block cipher is to divide the plaintext into groups with equal length, encrypt a group of data each time until the whole plaintext is encrypted, and then splice the ciphertext blocks to form ciphertext.
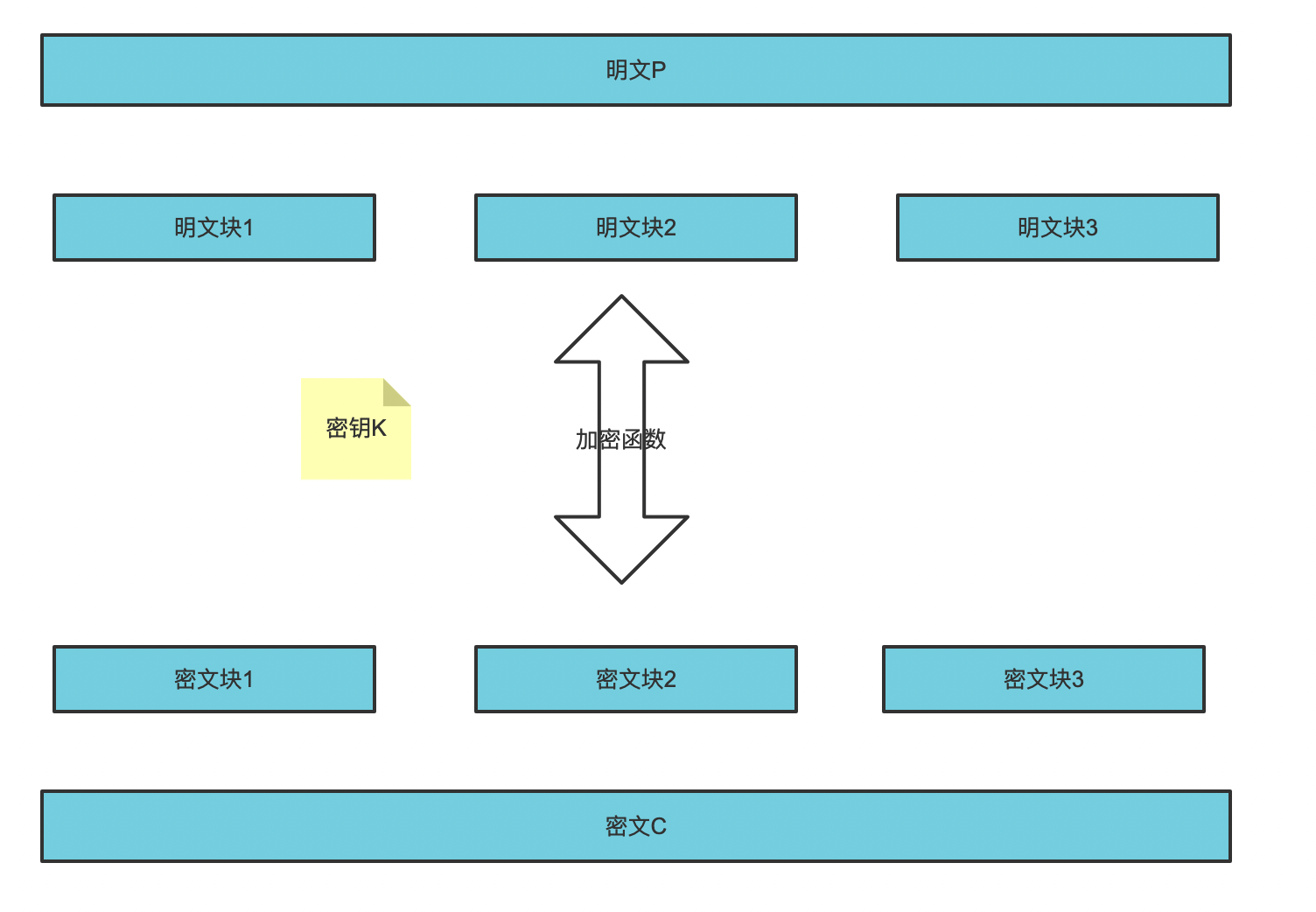
In the AES Standard Specification, the packet length can only be 128 bits, that is, each packet is 16 bytes (8 bits per byte).
The key length can be 128 bits, 192 bits or 256 bits. The recommended number of encryption rounds varies with the length of the key.
| AES | Key length (32 bit word) | Packet length (32 bit word) | Number of encryption rounds |
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 11 |
| AES-256 | 8 | 4 | 14 |
Fill mode
What does fill mode do? We can always see the filling mode in some AES encryption and decryption websites. When we encrypt and decrypt, we must select a filling mode.

This is because if the plaintext is not 128 bits (16 bytes), it needs to be filled, and the plaintext needs to be supplemented to an integer multiple of 16 bytes. When we encrypt and decrypt, we need to use the same filling method, otherwise we cannot decrypt successfully. Filling modes include: No Padding, PKCS5 Padding, PKCS7 Padding, ISO10126 Padding, Ansix923 Padding, Zero Padding, etc.
No Padding
No padding is required, but the plaintext must be an integer multiple of 16 bytes. If not, the user needs to implement the filling by himself. In addition to this mode, other filling modes will fill a 16 byte data if it is already 16 bytes of data.
PKCS5 Padding
Fill in the end of the plaintext. The filled data is the difference between the current and 16 bytes.
The plaintext length here is obviously less than 16 bytes, so it needs to be filled. If the length of plaintext is 14, the number of filled bytes is 2 and hexadecimal is 02 Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 After filling: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 02 02
PKCS7 Padding
Fill in the end of the plaintext. The filled data is the difference between the current and 16 bytes.
If the length of plaintext is 14, the number of filled bytes is 2 and hexadecimal is 02 Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 After filling: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 02 02
ISO10126 Padding
Fill in at the end of the plaintext. The difference between the current and 16 bytes is filled in at the end, and the remaining bytes are filled in random numbers.
The difference between the current and 16 bytes is written at the end, so the penultimate byte after filling is filled with random numbers, and the last byte is the difference between the current and 16 bytes. Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 After filling: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 01 02
Ansix923 Padding
The last byte is filled with the length of the byte sequence, and the remaining bytes are filled with the number 0.
Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 After filling: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 00 02
Zero padding
- Fill in the following zeros, and fill in as many zeros as you lack
Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 After filling: plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 00 00
In addition to the filling mode of No padding, other filling modes will fill a 16 byte data if it is already 16 bytes of data
Plaintext: 70 61 73 77 6 f 72 64 54 65 78 74 43 61 73 65
After filling:{70 61 73 73 77 6f 72 64 54 65 78 74 43 61 73 65 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00}
Encryption mode
ECB (electronic codebook) mode
When using ECB mode encryption, the same plaintext packet will be converted into the same ciphertext packet. We can split it into a huge corresponding table of "plaintext packet - > ciphertext packet". Therefore, ECB mode is also called codebook mode.
As mentioned above, "AES is block cipher. Block cipher is to divide plaintext into groups with equal length, and encrypt a group of data each time until a complete plaintext is encrypted". Is to divide the data into different groups (blocks) for encryption. After encryption, the encrypted data is spliced together.
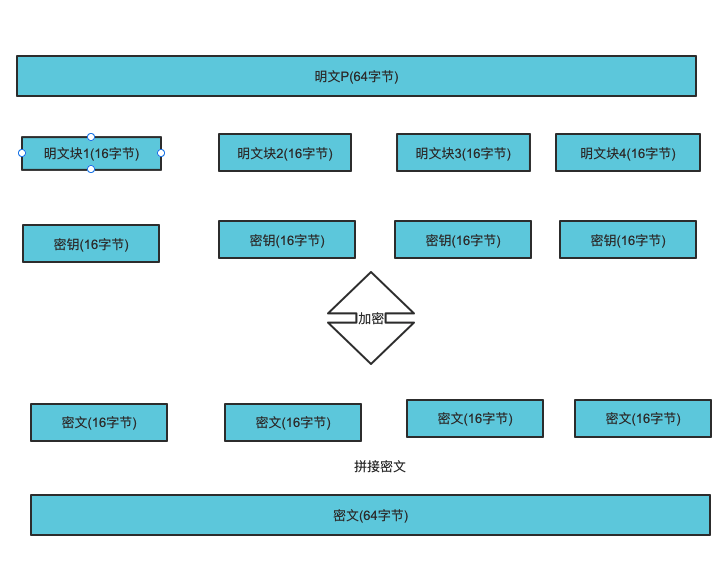
advantage
- Simple, fast and parallel;
shortcoming
- If the plaintext blocks are the same, the generated ciphertext blocks are also the same, which will reduce the security;
- ECB mode is vulnerable to attack, and the attacker can manipulate plaintext without decoding the password;

CBC(Cipher Block Chaining) mode
In order to solve the disadvantage of the same ciphertext block in ECB mode, CBC mode introduces the concept of an initial vector (iv), which must be a data with the same length as the key. Before the first encryption, the initial vector will be used to perform XOR operation with the first block of data, and the generated new data will be encrypted. Before encrypting the second block, It will take the first ciphertext data and the second plaintext for XOR operation and then encrypt, and so on. During decryption, that is, after decryption, XOR operation will be carried out to generate the final plaintext.
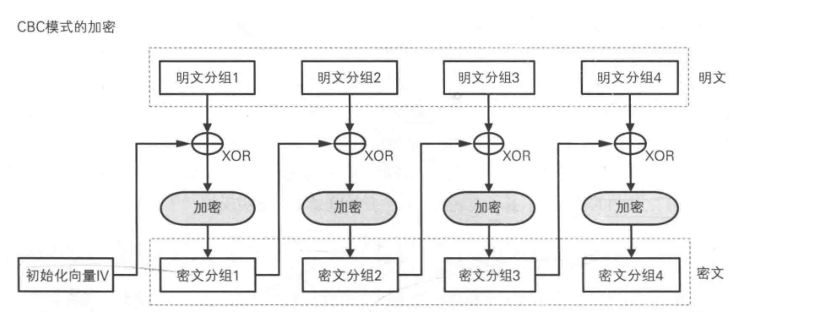
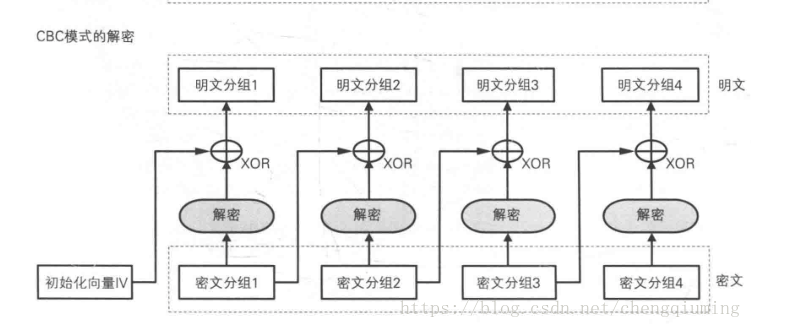
When using CBC mode, you should pay attention to the following points:
- The vector must be data equal to the length of the key.
- Because XOR operation will be performed before encryption and after decryption, our plaintext can not be completed, not a multiple of 16 bytes, and 0 will be automatically completed for XOR operation in CBC.
- During decryption, XOR operation will be performed after decryption to ensure successful data decryption.
- Due to the automatic completion, the decrypted data will also complete 0 later. Therefore, when obtaining the data, you need to remove the end 0 or intercept the decrypted data according to the length of the source data
advantage
- Each encryption key is different, which improves the security;
shortcoming
- Encryption cannot be performed in parallel, but decryption can be performed in parallel. The latter block can only be encrypted after the previous block is encrypted, and 0 needs to be filled in the back, so it is not suitable for streaming data (the reason for the inapplicability may be that it needs to meet the 128 bit data before encryption, so there will be no complement of 0)
- If the previous data is encrypted incorrectly, the subsequent data is wrong
- Both ends need to agree on the initial vector iv at the same time
CTR(Counter calculator) mode
CTR mode is a stream cipher that generates a key stream by encrypting the counter accumulated step by step.
In CTR mode, each packet corresponds to a counter accumulated step by step, and the counter is encrypted to generate a key stream. That is, the final ciphertext packet is obtained by XOR with the plaintext packet through the bit sequence obtained by encrypting the counter.
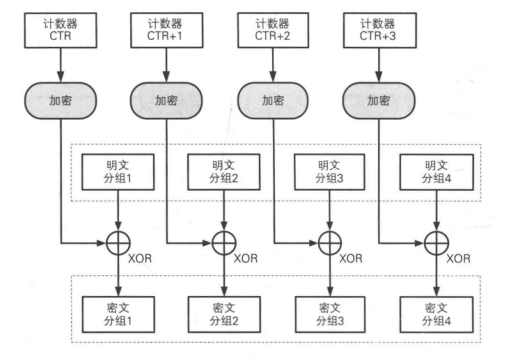
Each encryption generates a different value as the initial value of the counter. When the length of the counter is 128bit, as shown in the figure below:

advantage
- The encryption and decryption of CTR mode use the same mode, so it is easy to implement in the program.
- In CTR mode, packets can be encrypted and decrypted in any order, because the value of "counter" used in encryption and decryption can be directly calculated by nonce and packet sequence number.
- The ability to process packets in any order means that parallel computing can be realized. In the system supporting parallel computing, the speed of CTR mode is very fast.
- Assuming that one bit in the ciphertext packet of CTR mode is reversed, only the corresponding bit in the plaintext packet will be reversed after decryption, and this error will not be amplified.
- In CTR mode, if a packet of the key stream happens to be the same after encryption and before encryption, the key stream after the packet will become the constant repetition of the same value. This problem does not exist in CTR.
OFB(Output FeedBack) mode
This mode is similar to CFB. OFB mode does not directly encrypt plaintext through cryptographic algorithm, but generates "ciphertext grouping" by XOR between "plaintext grouping" and "output of cryptographic algorithm". It encrypts the data encrypted by iv or the previous iv, and the generated key performs XOR operation with plaintext. The same method is used for decryption, which uses the symmetry of XOR operation for encryption and decryption. Except for this, the rest are consistent with CFB.
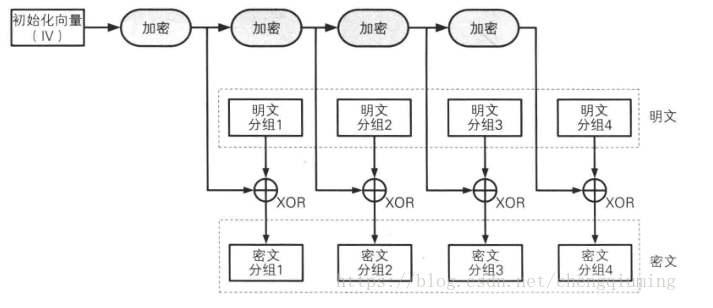
In OFB mode, the input of the cryptographic algorithm is the previous output of the cryptographic algorithm, that is, the output is fed back to the cryptographic algorithm, so it has the name of "output feedback mode".
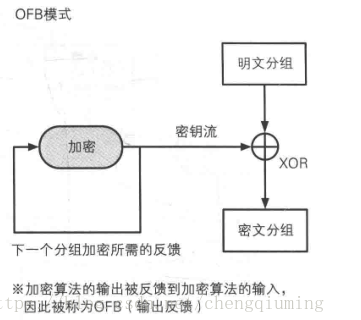
advantage
In OFB mode, the bit sequence (key stream) required by XOR can be generated by cryptographic algorithm in advance, which is independent of plaintext grouping. As long as the required key stream is prepared in advance, there is no need to use cryptographic algorithm in the actual process of generating ciphertext from plaintext, as long as the plaintext and key stream are XOR. Compared with AES and other cryptographic algorithms, XOR operation is very fast. This means that encryption can be completed quickly as long as the key flow is ready in advance. From another point of view, the operation of generating key stream and XOR operation can be parallel.
CFB(Cipher FeedBack) mode
This mode is similar to CBC mode, which can change block cipher into self synchronous stream cipher; The working process is very similar. The decryption process of CFB is almost the encryption process of reversed CBC.
When generating the first ciphertext packet, since there is no data of the previous output, it is necessary to use the initialization vector (IV) instead. Therefore, each time we encrypt, we need to generate a different random bit sequence as the initialization vector.
First, use a shift register with the same size as the block (key), initialize the register with IV, then encrypt the contents of the register with the block (key) password, and then XOR the highest x bit of the result with the X bit of plaintext to generate the X bit of ciphertext. Next, move the generated x-bit ciphertext into the register and repeat the process for the following x-bit plaintext. The decryption process is similar to the encryption process. Starting with IV, encrypt the register, XOR the high x bits of the result with the ciphertext, generate x-bit plaintext, and then move the lower x bits of the ciphertext into the register.
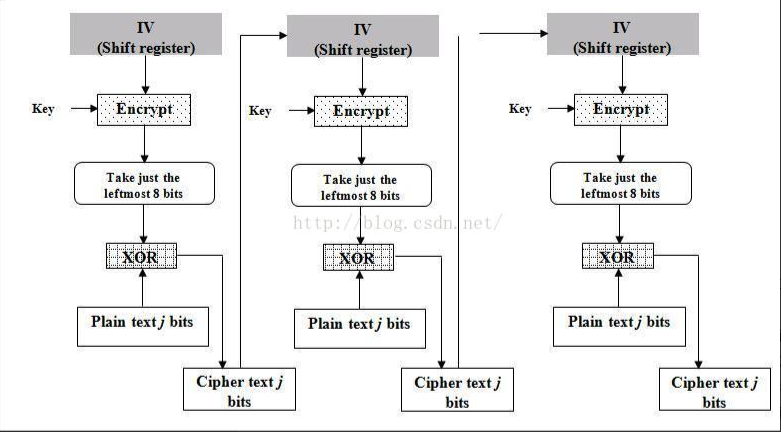
In CFB mode, the input of cryptographic algorithm is the previous ciphertext group, that is, the ciphertext group is fed back to the cryptographic algorithm, so it has the name of "ciphertext feedback algorithm".
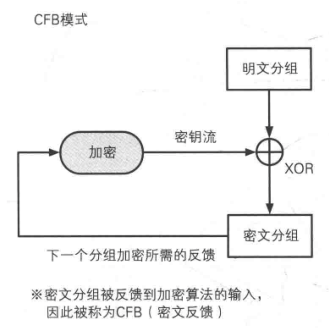
advantage
- Similar to CBC, the decryption process can be parallelized.
shortcoming
- The change of plaintext will affect all subsequent ciphertext, so the encryption process cannot be parallelized.
Encryption and decryption principle of AES
As mentioned above, AES keys support three lengths: AES128, AES192 and AES256. The length of the key determines the number of rounds of AES encryption. And Round in different stages has different processing steps. We can divide it into initial Round, ordinary Round and final Round.
In the initial round, it only does one operation: add round key
There are four operation steps for a normal round: ① sub bytes, ② shift rows, ③ mix columns, and ④ add round key
The final round has three operation steps: ① byte substitution (SubBytes), ② line shift (ShiftRows), and ③ round key addition (AddRoundKey). Note that in the final round, no columns confuse this operation.
The overall structure diagram of AES is as follows:
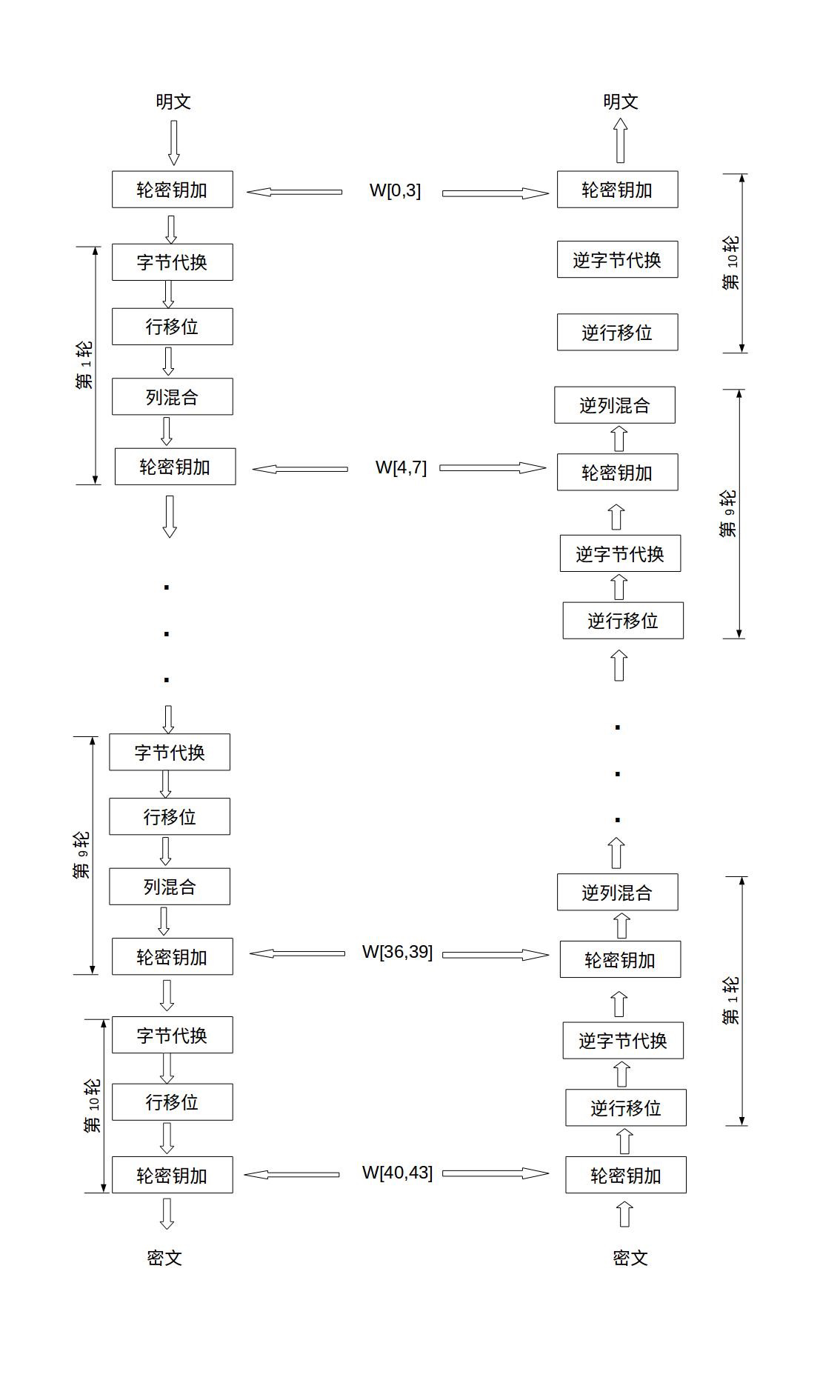
Let's take a look at what each operation does?
AES encryption
Initial round key addition
The initial round of key addition is to XOR between plaintext and key. The operation is as follows:
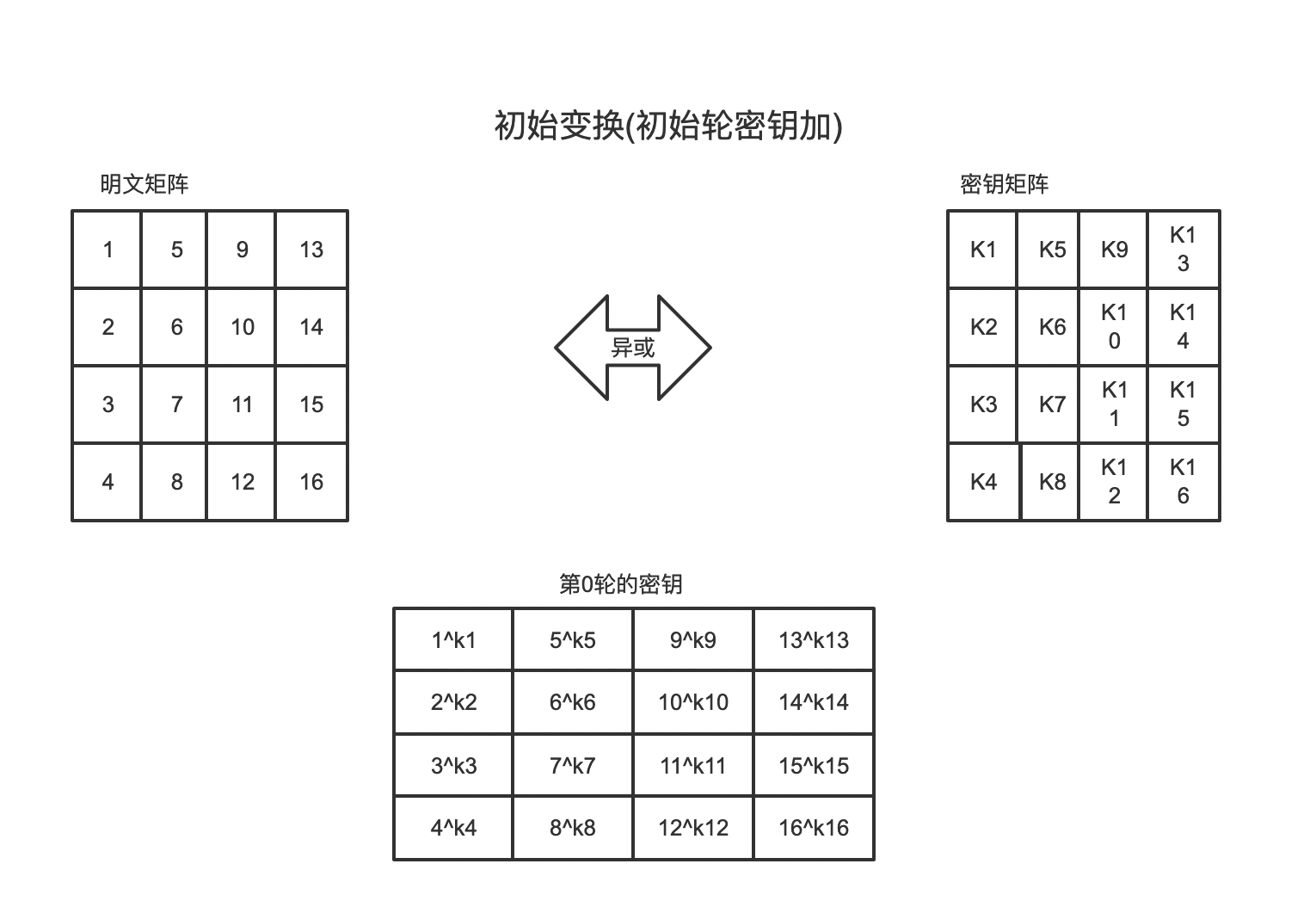
w[0,3] can be regarded as this. The first four elements w [0], w [1], w [2], and w [3] of the sequence are the original key, which is used for the initial key addition in the encryption operation. The last 40 words are divided into 10 groups, with 4 words (128 bits) in each group used for round key addition in 10 rounds of encryption operation.
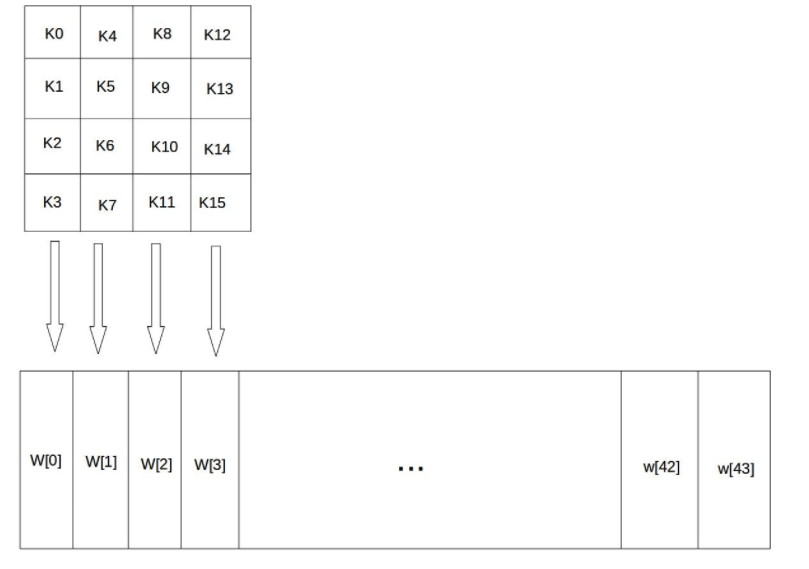
Key extension
In the above figure, we can see that there is a two-dimensional array with a length of 44. This array expands the key matrix into a sequence W[0],W[1],..., W[43] composed of 44 bytes through the key arrangement function. The first four elements W[0],W[1],W[2],W[3] of the sequence are the original keys, which are used for the initial key addition in the encryption operation. The last 40 words are divided into 10 groups, with 4 words (128 bits) in each group used for round key addition in 10 rounds of encryption operation.
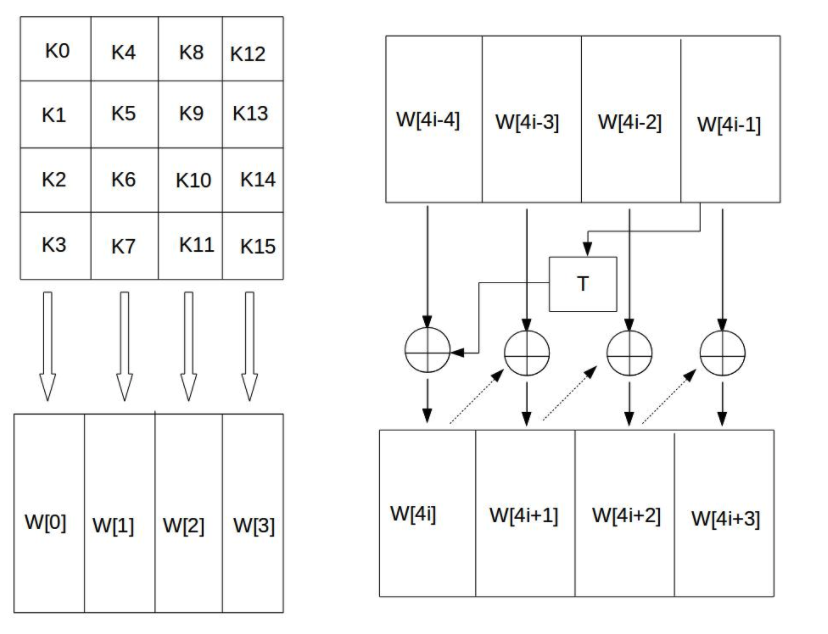
The four bytes in each column of the 44 matrix form a word. The four words in the four columns of the matrix are named W[0], W[1], W[2] and W[3], which form an array W in word units. For example, if the key K is set to "abcdefghijklmnop", then K0 = 'a', K1 = 'b', K2 = 'c', K3 ='d ', W[0] = "abcd", W[1] = "efgh". Then we need to expand the remaining 40 new columns of the W array to form a key expansion array with a total of 44 columns. The calculation method is as follows:
- If I is not a multiple of 4, column I is determined by the following equation: W[i] = W[i-4] xor W[i-1];
- If I is a multiple of 4, column I is determined by the following equation: W[i] = W[i-4] xor T(W[i-1]);
We can see that when i is a multiple of 4, a T function appears. This T function consists of three parts: word loop, byte substitution, round constant XOR.
The round constant Rcon[j] is a word, and its value is shown in the table below.
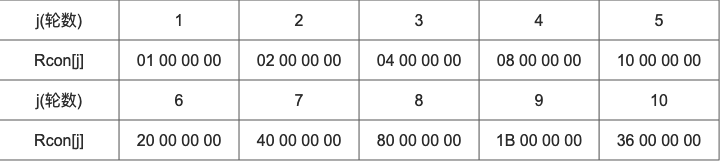
Let's take an example:
Arbitrarily assume that a 128 bit initial key is 3C A1 0b 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD (from top to bottom, from left to right). In this figure, we require W[4], and we find that 4 is a multiple of 4, so we use this equation: W[i] = W[i-4] xor T(W[i-1]), that is, W[4] = W[0] xor T(W[3]).
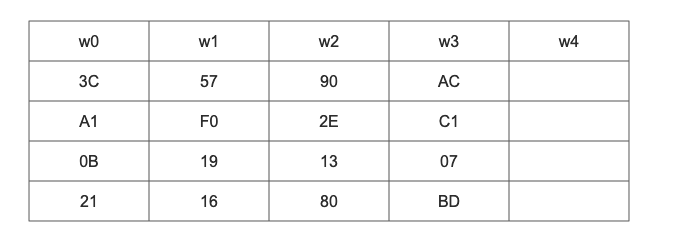
The value of W[3] is our original key, so we substitute W[3] into the T function.
- First, the word cycle is to move the four bytes of a word by one byte to the left. That is, {AC,C1,07,BD} becomes {C1,07,BD,AC}.
- Byte substitution: use S-box for byte substitution for the result of word cycle. Take {C1,07,BD,AC} as the input of S-box, and the output is {78,C5,7A,91}.
- The result of byte substitution is XOR calculated with the first round constant Rcon[1], and {79,C5,7A,91} will be obtained. Then perform XOR operation with W[0], W[4] = {3C,A1,0B,21} xor {79,C5,7A,91} = {45,64,71,B0}.
W[4] is calculated above, which is the case for W[5], W[6] and W[7]. After calculating W[4], W[5], W[6] and W[7], the sub key matrix to be used in the first round has been calculated.
Byte Substitution
Byte substitution of AES is a simple table lookup operation. AES defines an S-box and an inverse S-box. S-box is used for encryption; The inverse S-box is used for decryption.
The elements in the state matrix are mapped into a new byte in the following way: take the upper 4 bits of the byte as the row value and the lower 4 bits as the column value, and take out the elements of the corresponding row in the S-box or inverse S-box as the output. For example, when encrypting, if the output byte S1 is 0x12, check the row 0x01 and column 0x02 of the s box to get the value 0xc9, and then replace the original 0x12 of S1 with 0xc9. The diagram of state matrix after byte substitution is as follows:
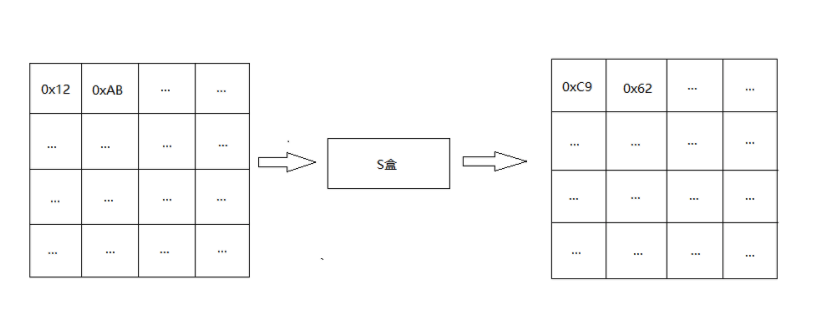
Row shift
Row shift is a simple left cyclic shift operation. State matrix: shift 0 byte left in row 0, 1 byte left in row 1, 2 bytes left in Row 2, and 3 bytes left in row 3. As shown in the figure below:
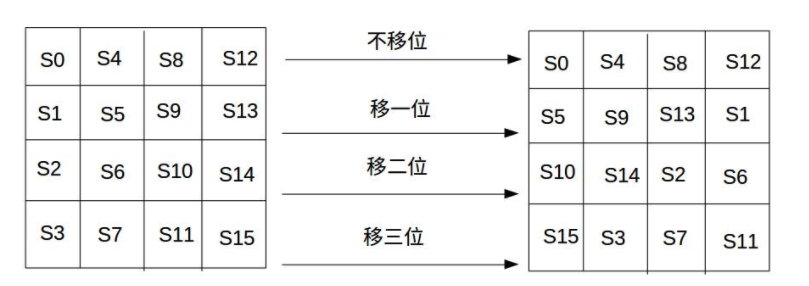
If decrypted, shift the bit to the right. The state matrix: shift 0 byte to the right in row 0, 1 byte to the right in row 1, 2 bytes to the right in Row 2 and 3 bytes to the right in row 3.
Column mixing
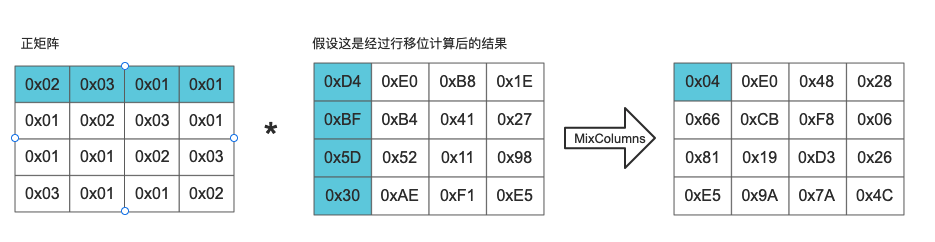
Column mixing transformation is realized by matrix multiplication. The state matrix after row shift is multiplied by the fixed matrix to obtain the confused state matrix.

The positive matrix in the figure below is given.
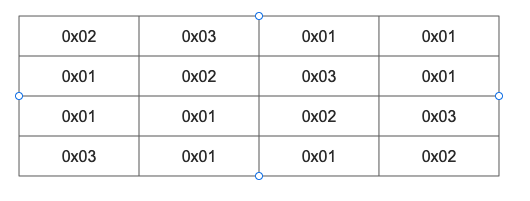
The column mixing of column j (0 < = j < = 3) in the state matrix can be expressed as shown in the following figure:
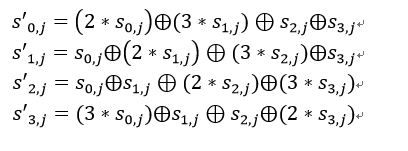
Among them, the multiplication and addition of matrix elements are binary operations based on GF(2^8), not multiplication and addition in the general sense. The addition of this binary operation is equivalent to the XOR of two bytes, and the multiplication is a little more complex. For an 8-bit binary number, using the multiplication on the field multiplied by (00000010) is equivalent to shifting 1 bit to the left (the low bit complements 0), and then XOR with (00011011) according to the situation (whether the highest bit of the binary is 0).
We set an 8-bit binary number (a7a6a5a4a3a2aa1a0), such as S1=(10011001), such as 0x02 * S1, as shown in the figure below:
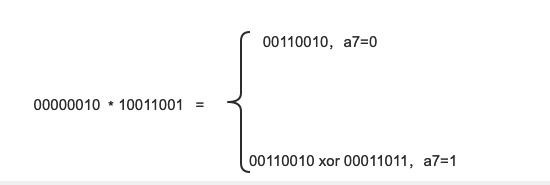
- If a7 is 1, multiply first and then XOR with 00011011, otherwise it will not be performed;
Case:
We first get the result of row shift calculation and start the calculation according to the given positive matrix. It can be substituted according to the formula below:
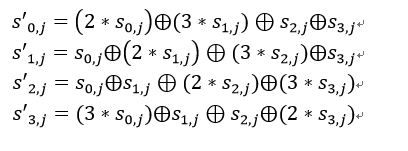
The sub cases of substitution formula are as follows: (0x02 * 0xD4) xor (0x03 * 0xBF) xor (0x01 * 0x5D) xor (0x01 * 0x30) = (10110011) xor (1101 1010) xor (0101 1101) xor (0011 0000) = 0000 0100 0x02:0000 0010 0xD4:1101 0100 0xD4 16 Binary is replaced by binary, and the highest bit is 1, so after multiplication, XOR operation with 00011011 is also required Mentioned in the article"For an 8-bit binary number, multiply by the multiplication on the field(00000010)Equivalent to shifting 1 bit left(Low complement 0)",So 0 xD4 Multiply by 0 x02 Get 1010 1000. Then perform XOR operation with 00011011 to obtain 10110011. 0x03:0000 0011 0x02:0000 0010 0x01:0000 0001 0xBF:1011 1111 0x02 And 0 x01 0 can be obtained by XOR x03,So we can write:(0x02 xor 0x01) * 0xBF (0x02 * 0xBF) xor 0xBF First calculate the multiplication 0xBF: 1011 1111 -> 0111 1110 Then XOR with 0001 1011 0111 1110 xor 0001 1011 = 0110 0101 After 0110, 0101 and 0 xBF Perform XOR to obtain 1101 1010. The final result is 0 x04.
Column hybrid decryption
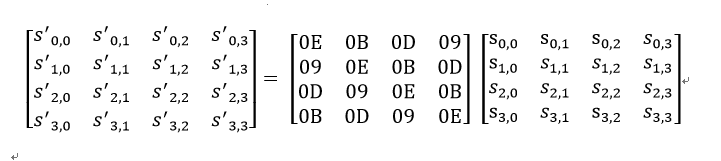
Decrypt in the same way as above. But the positive matrix is replaced by the inverse matrix, which is also a given matrix.
Round key addition
Through the key arrangement function, the key matrix is expanded into a sequence W[0],W[1],..., W[43] composed of 44 bytes. The first four elements W[0],W[1],W[2],W[3] of the sequence are the original keys, which are used for the initial key addition in the encryption operation. The last 40 bytes are divided into 10 groups, and 4 bytes (128 bits) in each group are used for round key addition in 10 rounds of encryption operation.
In the above key expansion, we have introduced how the key matrix is expanded into a sequence of 44 bytes through a case. When we perform the first round of encryption, we need to calculate the round key addition to be used in the first round, that is, W[4], W[5], W[6] and W[7].
First, we need to get the state matrix after column mixing, and then perform bit by bit XOR operation with 128 bit round key according to this state matrix.
Case:
Suppose that after column mixing, the result is:
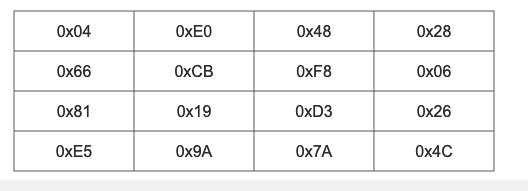
The first key matrix result is:
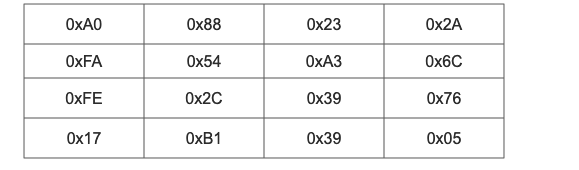
The round key addition result of the first round is obtained by XOR between the column mixing result and the sub key matrix result.
For example: 0x04 xor 0xAO = 0xA4
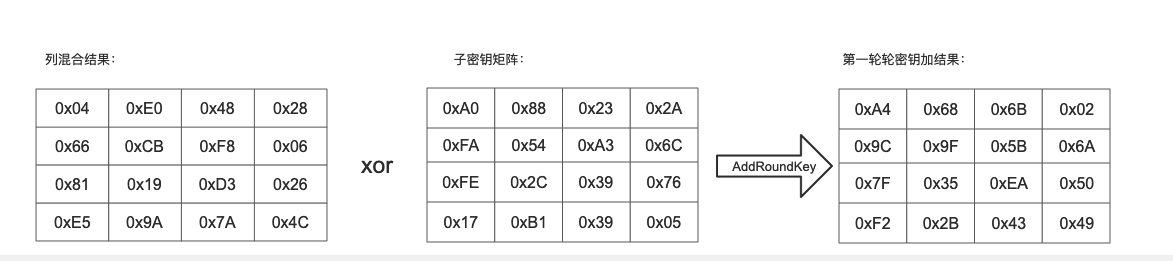
The inverse operation of round key addition is completely consistent with the forward round key addition, because the inverse operation of XOR is itself. Round key addition is very simple, but it can affect every bit in the S array.
AES decryption
In the figure at the beginning of the article, there is a flow chart of AES decryption, which can be decrypted according to that flow chart. Another equivalent decryption mode is introduced below, and the flow chart is shown in the figure below. This equivalent decryption mode makes the use order of each transformation in the decryption process consistent with that in the encryption process, except that the inverse transformation is used to replace the original transformation.
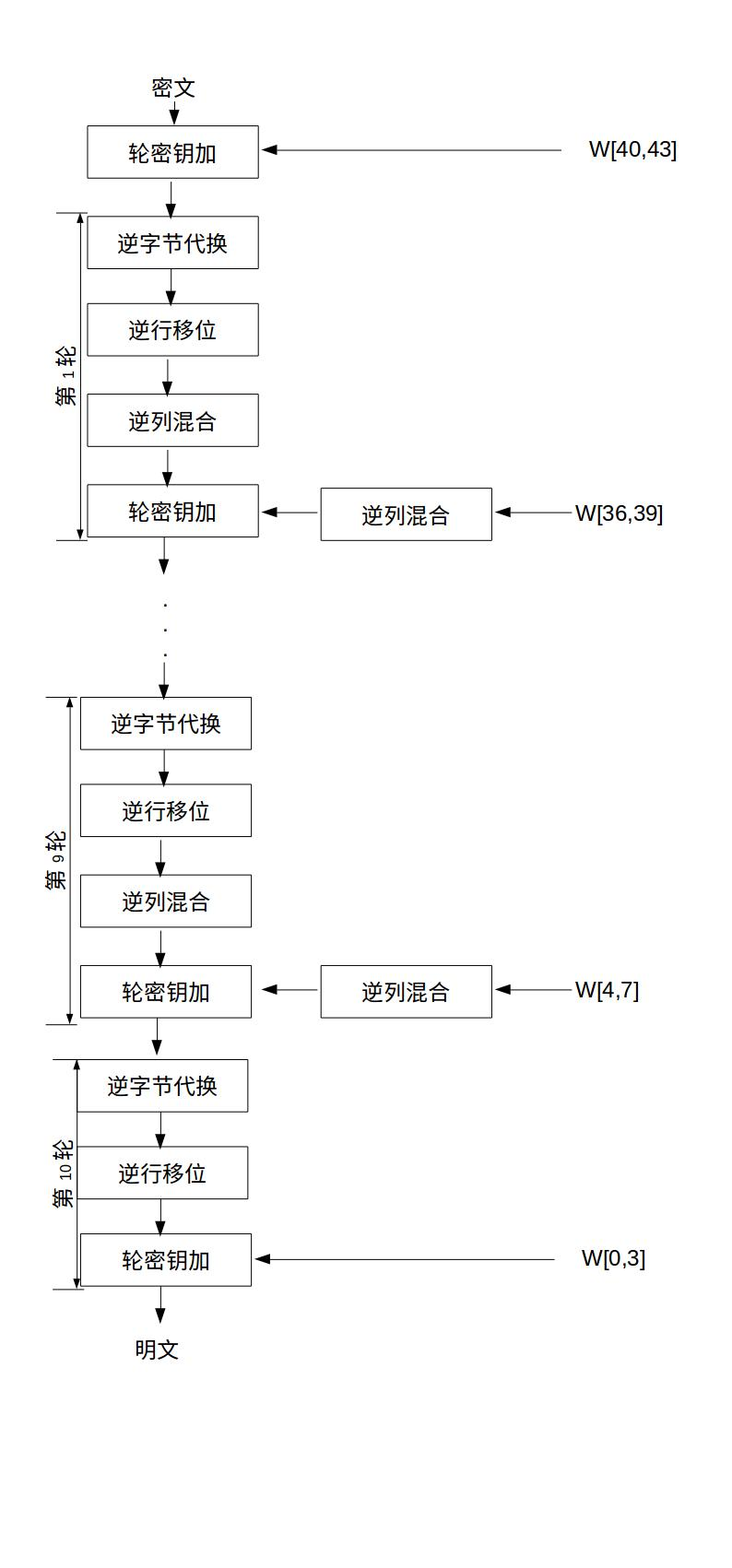
AES algorithm implementation (Java version)
Given matrix constant
package com.hbh.AESTest.constant;
public interface AESConstants {
/**
* For mixed positive columns
*/
short[][] CX = {
{0x02, 0x03, 0x01, 0x01},
{0x01, 0x02, 0x03, 0x01},
{0x01, 0x01, 0x02, 0x03},
{0x03, 0x01, 0x01, 0x02},
};
// Inverse transformation matrix for column mixing
short[][] INVERSE_CX = {
{0x0E, 0x0B, 0x0D, 0x09},
{0x09, 0x0E, 0x0B, 0x0D},
{0x0D, 0x09, 0x0E, 0x0B},
{0x0B, 0x0D, 0x09, 0x0E},
};
short[] LEFT_SHIFT_TABLE = {1, 2, 3, 0};
short[] INVERSE_LEFT_SHIFT_TABLE = {1, 2, 3, 0};
// Round constant array
short[][] R_CON = {
{0x00, 0x00, 0x00, 0x00},
{0x01, 0x00, 0x00, 0x00},
{0x02, 0x00, 0x00, 0x00},
{0x04, 0x00, 0x00, 0x00},
{0x08, 0x00, 0x00, 0x00},
{0x10, 0x00, 0x00, 0x00},
{0x20, 0x00, 0x00, 0x00},
{0x40, 0x00, 0x00, 0x00},
{0x80, 0x00, 0x00, 0x00},
{0x1b, 0x00, 0x00, 0x00},
{0x36, 0x00, 0x00, 0x00},
};
// A matrix for determining the cyclic left shift rule of bytes between words in line shift transformation of encryption operation
short[][] SHIFTING_TABLE = {
{0, 1, 2, 3},
{1, 2 ,3, 0},
{2, 3, 0, 1},
{3, 0, 1, 2},
};
// A matrix for determining the cyclic left shift rule of inter word bytes in the line shift transformation of decryption operation
short[][] INVERSE_SHIFTING_TABLE = {
{0, 3, 2, 1},
{1, 0 ,3, 2},
{2, 1, 0, 3},
{3, 2, 1, 0},
};
/**
* s box
*/
short[][] SUBSTITUTE_BOX = {
{0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76},
{0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0},
{0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15},
{0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75},
{0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84},
{0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf},
{0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8},
{0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2},
{0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73},
{0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb},
{0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79},
{0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08},
{0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a},
{0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e},
{0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf},
{0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16},
};
/**
* Inverse s-box
*/
short[][] INVERSE_SUBSTITUTE_BOX = {
{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},
{0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},
{0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},
{0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},
{0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},
{0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},
{0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},
{0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},
{0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},
{0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},
{0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},
{0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},
{0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},
{0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},
{0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},
{0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d},
};
}
Encryption and decryption core logic
package com.hbh.AESTest.core;
import com.hbh.AESTest.constant.AESConstants;
import com.hbh.AESTest.operation.*;
/**
* @program: java_basis
* @description:
* @author: hbh
* @create: 2022-02-05 16:10
*/
public class AESCore {
/**
*
* @param initialPTState Status array of plaintext or ciphertext
* @param roundKeys Round key array to be used for encryption and decryption
* @param substituteTable S-box for encryption and decryption
* @param mixColumnTable An array used to replace or reduce polynomials in column mixing
* @param shiftingTable In line transformation, an array of bits used to determine the left shift between words
* @return
*/
public static short[][] coreEncrypt(short[][] initialPTState, short[][][] roundKeys, short[][] substituteTable, short[][] mixColumnTable, short[][] shiftingTable){
// Initial round key addition, XOR operation
short[][] state = InitialUtils.xor(roundKeys[0],initialPTState);
// Nine rounds of transformation before processing
for (int i = 0; i < 9; i++) {
// Replace the byte of the status array with the byte of the corresponding position in the S-box
state = RoundKeyExtensionUtils.substituteState(state, substituteTable);
// Row shift transform
state = ShiftRow.shiftRows(state, shiftingTable);
// Column mixing transformation
state = MixColumn.mixColumns(state, mixColumnTable);
// Round key plus transformation
state = InitialUtils.xor(roundKeys[i + 1], state);
}
// Process the last round
state = RoundKeyExtensionUtils.substituteState(state, substituteTable);
state = ShiftRow.shiftRows(state, shiftingTable);
state = InitialUtils.xor(roundKeys[roundKeys.length - 1], state);
return state;
}
/**
* Decryption logic: by extracting the reversible operation into a reversible matrix, reuse the encryption core function
* @param encryptedTextState initial encrypted text state
* @param keyState initial key state
* @return decrypted state
*/
public static short[][] coreDecrypt(short[][] encryptedTextState, short[][] keyState) {
// obtain raw round keys
short[][] rawRoundKeys = RoundKeyExtensionUtils.generateRoundKeys(keyState);
// make it easier to obtain a whole block of round key in a round transformation
short[][][] roundKeys = transfer(rawRoundKeys); // Make the key extension into a three-dimensional array
// Inverse column hybrid transformation is performed on the middle 9 keys
for (int i = 1; i < roundKeys.length - 1; i++) {
roundKeys[i] = MixColumn.mixColumns(roundKeys[i], AESConstants.INVERSE_CX);
}
short[][][] inverseRoundKeys = inverseRoundKeys(roundKeys);
return coreEncrypt(encryptedTextState, inverseRoundKeys, AESConstants.
INVERSE_SUBSTITUTE_BOX, AESConstants.INVERSE_CX, AESConstants.INVERSE_SHIFTING_TABLE);
}
/**
* [Decryption] reverse the decryption extended key array to facilitate the reuse of core encryption operations,
* @param roundKeys Decrypt extended key array
* @return Decryption extended key array reversed
*/
private static short[][][] inverseRoundKeys(short[][][] roundKeys) {
short[][][] result = new short[roundKeys.length][4][4];
int length = roundKeys.length;
for (int i = 0; i < roundKeys.length; i++) {
result[i] = roundKeys[length - 1 - i];
}
return result;
}
private static short[][][] transfer(short[][] origin) {
short[][][] result = new short[origin.length / 4][4][4];
for (int i = 0; i < origin.length / 4; i++) {
short[][] temp = new short[4][4];
System.arraycopy(origin, i * 4, temp, 0, 4);
result[i] = temp;
}
return result;
}
}
Initial transformation
package com.hbh.AESTest.operation;
/**
* @program: java_basis
* @description: Initial transformation operation tool class
* @author: hbh
* @create: 2022-02-05 13:57
*/
public class InitialUtils {
/**
*
* @param first Plaintext
* @param second secret key
* @return
*/
public static short[][] xor(short[][] first, short[][] second){
short[][] res = new short[first.length][4];
for (int i = 0; i < first.length; i++) {
for (int j = 0; j < second.length; j++) {
res[i][j] = (short) (first[i][j] ^ second[i][j]);
}
}
return res;
}
}
Row shift
package com.hbh.AESTest.operation;
/**
* @program: java_basis
* @description: Row displacement transformation: it belongs to displacement and linear transformation. Its essence is to disrupt and rearrange the data and play the role of diffusion
* @author: hbh
* @create: 2022-02-05 16:00
*/
public class ShiftRow {
/**
* Row shift transformation, which circularly shifts the rows in the state to the left
* @param state
* @param shiftingTable
* @return
*/
public static short[][] shiftRows(short[][] state, short[][] shiftingTable){
short[][] result = new short[state.length][4];
for (int i = 0; i < 4; i++) {
for (int j = 0; j < state.length; j++) {
result[j][i] = state[shiftingTable[j][i]][i];
}
}
return result;
}
}
Key extension
package com.hbh.AESTest.operation;
import com.hbh.AESTest.constant.AESConstants;
/**
* @program: java_basis
* @description: Key extension
* @author: hbh
* @create: 2022-02-05 14:22
*/
public class RoundKeyExtensionUtils {
/**
* Key extension
* @param originalKey Original key
* @return Return key extension
*/
public static short[][] generateRoundKeys(short[][] originalKey){
short[][] roundKeys = new short[44][4];
int keyWordCount = originalKey.length;
System.arraycopy(originalKey,0,roundKeys,0,keyWordCount); // The original key is used here
for (int i = keyWordCount; i < keyWordCount * 11; i++) {
short[] temp = roundKeys[i-1];
if(i % keyWordCount == 0){
// If i is a multiple of 4, a T function will be performed here
/**
* T Function operations include the following:
* 1. Word cycle
* 2. Byte Substitution
* 3. Round constant XOR (given)
*/
temp = xor(substituteWord(leftShift(temp)), AESConstants.R_CON[i / keyWordCount]);
}
// If i is not a multiple of 4, XOR directly
roundKeys[i] = xor(roundKeys[i - keyWordCount], temp);
}
return roundKeys;
}
/**
* Word cycle: cycle in bytes and shift left by 1 unit
* @param aWord
* @return
*/
public static short[] leftShift(short[] aWord) {
short[] result = new short[4];
for (int i = 0; i < 4; i++) {
result[i] = aWord[AESConstants.LEFT_SHIFT_TABLE[i]];
}
return result;
}
/**
* Byte substitution replaces each byte in a word
* @param aWord
* @return
*/
public static short[] substituteWord(short[] aWord) {
for (int i = 0; i < 4; i++) {
aWord[i] = substituteByte(aWord[i],AESConstants.SUBSTITUTE_BOX);
}
return aWord;
}
/**
* Byte substitution: take the upper four bits and the lower four bits of a word as the row number and column number of the S box respectively, and use the row and column number to take the bytes in the S box to replace the original bytes
* @param originalByte
* @param substituteTable
* @return
*/
public static short substituteByte(short originalByte, short[][] substituteTable) {
int low4Bits = originalByte & 0x000f;
int high4Bits = (originalByte >> 4) & 0x000f;
return substituteTable[high4Bits][low4Bits];
}
/**
* XOR operation between two words
* @param first
* @param second
* @return
*/
public static short[] xor(short[] first, short[] second) {
short[] result = new short[4];
for (short i = 0; i < 4; i++) {
result[i] = (short) (first[i] ^ second[i]);
}
return result;
}
/**
* Status substitution: word substitution is performed for each word in the status
*/
public static short[][] substituteState(short[][] state, short[][] substituteTable) {
for (int i = 0; i < state.length; i++) {
for (int j = 0; j < 4 ; j++) {
state[i][j] = substituteByte(state[i][j], substituteTable);
}
}
return state;
}
}
Column mixing
package com.hbh.AESTest.operation;
/**
* @program: java_basis
* @description: Column mixing transformation
* @author: hbh
* @create: 2022-02-05 16:05
*/
public class MixColumn {
/**
* Column mixing transformation
*
* @param state Status array
* @param table Polynomial equivalent matrix
* @return New state after column mixing transformation
*/
public static short[][] mixColumns(short[][] state, short[][] table) {
short[][] result = new short[state.length][4];
for (int i = 0; i < state.length; i++) {
result[i] = matrixMultiply(state[i], table);
}
return result;
}
private static short[] matrixMultiply(short[] aWord, short[][] table) {
short[] result = new short[4];
for (int i = 0; i < 4; i++) {
result[i] = wordMultiply(table[i], aWord);
}
return result;
}
private static short wordMultiply(short[] firstWord, short[] secondWord) {
short result = 0;
for (int i = 0; i < 4; i++) {
result ^= multiply(firstWord[i], secondWord[i]);
}
return result;
}
private static short multiply(short a, short b) {
short temp = 0;
while (b != 0) {
if ((b & 0x01) == 1) {
temp ^= a;
}
a <<= 1;
if ((a & 0x100) > 0) {
a ^= 0x1b;
}
b >>= 1;
}
return (short) (temp & 0xff);
}
}
package com.hbh.AESTest.serivce;
public interface CipherService {
/**
* encryption
* @param plainText Plaintext to be encrypted
* @param key secret key
* @return
*/
String encrypt(String plainText, String key);
/**
* decrypt
* @param encryptedText Ciphertext to be decrypted
* @param key
* @return
*/
String decrypt(String encryptedText, String key);
}
External interface
package com.hbh.AESTest.serivce;
import com.hbh.AESTest.constant.AESConstants;
import com.hbh.AESTest.core.AESCore;
import com.hbh.AESTest.operation.InitialUtils;
import com.hbh.AESTest.operation.MixColumn;
import com.hbh.AESTest.operation.ShiftRow;
import com.hbh.AESTest.util.ArrayUtil;
import com.hbh.AESTest.operation.RoundKeyExtensionUtils;
import com.hbh.AESTest.util.Base64Util;
import org.junit.Test;
import java.util.Arrays;
/**
* @program: java_basis
* @description:
* @author: hbh
* @create: 2022-02-05 16:34
*/
public class AESCipherServiceImpl implements CipherService{
public static void main(String[] args) {
String plaintext = "passwordTextCase", key = "simpleKeyCase123";
CipherService aesService = new AESCipherServiceImpl();
String encryptedText = aesService.encrypt(plaintext, key);
String decrypt = aesService.decrypt(encryptedText, key);
ArrayUtil.printInfo("Original text:", plaintext, false);
ArrayUtil.printInfo("Key:", key, false);
ArrayUtil.printInfo("Ciphertext:", encryptedText, false);
ArrayUtil.printInfo("After decryption:", decrypt, false);
}
@Override
public String encrypt(String plainText, String key) {
System.out.println("##################### encryption #####################");
ArrayUtil.printInfo("Plaintext:", plainText, false);
ArrayUtil.printInfo("Key:", key, false);
short[][] initialPTState = transfer(ArrayUtil.transferToShorts(plainText));
ArrayUtil.printInfo("16 Binary plaintext:", getStateHex(initialPTState), false);
short[][] initialKeyState = transfer(ArrayUtil.transferToShorts(key));
ArrayUtil.printInfo("16 Binary key:", getStateHex(initialKeyState), true);
short[][] rawRoundKeys = RoundKeyExtensionUtils.generateRoundKeys(initialKeyState);// Generate key extension
System.out.println("Key extension:");
printRoundKeys(rawRoundKeys);
short[][][] roundKeys = transfer(rawRoundKeys); // Expand the key into a three-dimensional array, and each round can more quickly obtain the round key to be used in this round
/**
* initialPTState:
* roundKeys: Key extension, round key addition needs to be used
* AESConstants.SUBSTITUTE_BOX: S box
* AESConstants.CX: Column mixing given fixed matrix
* AESConstants.SHIFTING_TABLE: Matrix required for word cyclic left shift operation in key extension
*/
short[][] finalState = AESCore.coreEncrypt(initialPTState, roundKeys, AESConstants.SUBSTITUTE_BOX,
AESConstants.CX, AESConstants.SHIFTING_TABLE);
return Base64Util.encode(transfer2Bytes(finalState));
}
@Override
public String decrypt(String encryptedText, String key) {
System.out.println("##################### decryption #####################");
short[][] initialTextState = transfer(Base64Util.decodeToShorts(encryptedText));
short[][] initialKeyState = transfer(ArrayUtil.transferToShorts(key));
short[][] decryptState = AESCore.coreDecrypt(initialTextState, initialKeyState);
return getOrigin(decryptState);
}
/**
* Print round key array
* @param
*/
private void printRoundKeys(short[][] roundKeys) {
for (int i = 0, keyOrder = 1; i < roundKeys.length; i += 4, keyOrder++) {
String infoKValue = getStateHex(new short[][]{
roundKeys[i], roundKeys[i + 1],
roundKeys[i + 2], roundKeys[i + 3]
});
ArrayUtil.printInfo("[RoundKey " + keyOrder + "]", infoKValue, false);
}
System.out.println();
}
/**
* Hexadecimal string of status array
* @param
* @return
*/
private String getStateHex(short[][] state) {
StringBuilder builder = new StringBuilder();
for (short[] aWord : state) {
builder.append(toHexString(aWord));
}
return builder.toString();
}
/**
* Converts a word in bytes to a hexadecimal string
* @param
* @return
*/
private String toHexString(short[] aWord) {
StringBuilder builder = new StringBuilder();
for (short aByte : aWord) {
builder.append(toHexString(aByte));
}
return builder.toString();
}
/**
* Gets a hexadecimal string of one byte
* @param value
* @return
*/
private String toHexString(short value) {
String hexString = Integer.toHexString(value);
if (hexString.toCharArray().length == 1) {
hexString = "0" + hexString;
}
return hexString;
}
/**
* The two-dimensional array is transformed into a three-dimensional array, which is convenient to obtain the round key matrix of Nk x 4 through the round subscript in the round transformation
* @param origin Two dimensional round key array
* @return 3D wheel key array
*/
private short[][][] transfer(short[][] origin) {
short[][][] result = new short[origin.length / 4][4][4];
for (int i = 0; i < origin.length / 4; i++) {
short[][] temp = new short[4][4];
System.arraycopy(origin, i * 4, temp, 0, 4);
result[i] = temp;
}
return result;
}
/**
* Convert the matrix into Nb x 4 state matrix, which is used to obtain the initial state array of plaintext and key
* @param origin
* @return
*/
private short[][] transfer(short[] origin) {
short[][] result = new short[origin.length / 4][4];
for (int i = 0; i < result.length; i++) {
System.arraycopy(origin, i * 4, result[i], 0, 4);
}
// int limit = 0;
// // 0,0 1,0, 2,0 3,0
// for (int i = 0; i < result.length; i++) {
// for(int j = 0; j < result.length; j++){
// result[j][i] = origin[limit];
// limit ++;
// }
// }
return result;
}
/**
* The encrypted status array is converted into a byte array for Base64 coding
* @param finalState Encrypted status array
* @return Byte array corresponding to status array
*/
private byte[] transfer2Bytes(short[][] finalState) {
byte[] result = new byte[finalState.length * 4];
for (int i = 0;i < finalState.length; i++) {
for (int j = 0; j < 4; j++) {
result[i * 4 + j] = (byte) (finalState[i][j] & 0xff);
}
}
return result;
}
/**
* Restore the final decrypted short array to a string
* @param decryptState
* @return
*/
private static String getOrigin(short[][] decryptState) {
StringBuilder builder = new StringBuilder();
for (short[] shorts : decryptState) {
for (short s : shorts) {
builder.append(String.valueOf((char) s));
}
}
return builder.toString();
}
}
Output conversion array tool class
package com.hbh.AESTest.util;
import java.io.*;
import java.math.BigInteger;
/**
* @program: java_basis
* @description:
* @author: hbh
* @create: 2022-02-05 16:39
*/
public class ArrayUtil {
/**
* Convert a string to a one-dimensional short array
* transfer a string to short array
* @param string target string to be process
* @return a short array
*/
public static short[] transferToShorts(String string) {
byte[] bytes = string.getBytes();
int length = bytes.length;
short[] shorts = new short[length];
for (int i = 0; i < length; i++) {
shorts[i] = bytes[i];
}
return shorts;
}
/**
* print information for tracing the whole process
*
* @param key info type
* @param value info
* @param nextRow flag deciding whether going to next row
*/
public static String printInfo(String key, String value, boolean nextRow) {
String message = String.format("%-30s%-70s", key, value);
if (nextRow) {
message += "\n";
}
System.out.println(message);
return message;
}
/**
* concatenate two byte arrays
* @param before the first array in concat
* @param after the second array in concat
* @return concat
*/
public static byte[] concat(byte[] before, byte[] after) {
byte[] result = new byte[before.length + after.length];
System.arraycopy(before, 0, result, 0, before.length);
System.arraycopy(after, 0, result, before.length, after.length);
return result;
}
/**
* transfer int value into byte array
* @param intValue int value
* @return byte array
*/
public static byte[] int2Bytes(int intValue) {
byte[] byteArray = null;
try {
ByteArrayOutputStream byteOut = new ByteArrayOutputStream();
DataOutputStream dataOut = new DataOutputStream(byteOut);
dataOut.writeByte(intValue);
byteArray = byteOut.toByteArray();
} catch (IOException e) {
e.printStackTrace();
}
return byteArray;
}
/**
* segment one-dimension array into an 8x8 array
* transfer every byte unit into int
* transfer int into ascii type and print it
* @param chars char array to be processed
*/
public static String segmentAndPrintChars(char[] chars) {
char[][] chars1 = ArrayUtil.segmentDimension(chars, chars.length / 8 ,8);
StringBuilder builder = new StringBuilder();
for (char[] aChars1 : chars1) {
builder.append((char) Integer.parseInt(String.valueOf(aChars1), 2));
}
return builder.toString();
}
/**
* transfer byte array into char array
* @param bytes byte array to be transferred
* @return bits in chars format
*/
public static char[] bytesToChars(byte[] bytes) {
StringBuilder builder = new StringBuilder();
for (byte aByte : bytes) {
String aByteStr = Integer.toBinaryString(
(aByte & 0xff) + 0x0100).substring(1);
builder.append(aByteStr);
}
return builder.toString().toCharArray();
}
public static short[] byteToShorts(byte[] bytes) {
short[] result = new short[bytes.length];
for (int i = 0; i < bytes.length; i++) {
result[i] = (short) (bytes[i] & 0xff);
}
return result;
}
/**
* disrupt the order of an array by reindexing it
* @param chars original array to be disrupted
* @param newIndexes index array the disruption is according to
* @return disrupted sub array of chars
*/
public static char[] disruptArray(char[] chars, short[] newIndexes) {
char[] resultChars = new char[newIndexes.length];
for (int i = 0; i < newIndexes.length; i++) {
resultChars[i] = chars[newIndexes[i] - 1];
}
return resultChars;
}
/**
* byte array printing
* @param bytes byte array
*/
public static void printByteArray(byte[] bytes){
int length = bytes.length;
StringBuilder builder = new StringBuilder();
for (int i = 1; i <= length; i++) {
String symbol = (i % 8 == 0) ? " " : "";
builder.append((int) bytes[i - 1]).append(symbol);
}
System.out.println(builder.toString());
}
/**
* print bits in chars format and what it stands for
* @param prefix info
* @param chars bits in chars format to be printed
*/
public static String printBitChars(String prefix, char[] chars) {
int length = chars.length;
StringBuilder builder = new StringBuilder();
for (int i = 1; i <= length; i++) {
String symbol = (i % 8 == 0 || i == length)
? " " : "";
builder.append(chars[i - 1]).append(symbol);
}
String message = String.format("%-30s%-30s", prefix, builder.toString());
System.out.println(message);
return message;
}
/**
* char array printing
* @param chars char array to be printed
*/
public static void printArray(char[] chars) {
int length = chars.length;
for (int i = 1; i <= length; i++) {
String symbol = (i % 8 == 0 || i == length)
? "\n" : " ";
System.out.print(chars[i - 1] + symbol);
}
}
/**
* left shifting based on String operation
* @param src bits to be shifted in chars format
* @param length shifting length
* @return shifted bit sequences in chars format
*/
public static char[] leftShift(char[] src, int length) {
String byteString = String.valueOf(src);
return (byteString.substring(length) +
byteString.substring(0, length)).toCharArray();
}
/**
* xor operation
* @param aChars operating bits in chars format
* @param bChars operating bits in chars format
* @return result of operation, formatting in 48 or 64 bits
*/
public static char[] xor(char[] aChars, char[] bChars, int bits) {
BigInteger a = new BigInteger(String.valueOf(aChars), 2);
BigInteger b = new BigInteger(String.valueOf(bChars), 2);
BigInteger xorResult = a.xor(b);
String xorStr = xorResult.toString(2);
StringBuilder builder = new StringBuilder();
int sub = bits - xorStr.length();
if (sub > 0) {
for (int i = 0; i < sub; i++) {
builder.append("0");
}
xorStr = builder.toString() + xorStr;
}
return xorStr.toCharArray();
}
/**
* segment one-dimension array into a two-dimension array
* which holds data in rows x columns format
* @param chars one-dimension array
* @param rows rows of result
* @param columns columns of result
* @return a two-dimension array
* which holds data in rows x columns format
*/
public static char[][] segmentDimension(char[] chars, int rows, int columns) {
char[][] result = new char[rows][columns];
for (int i = 0; i < result.length; i++) {
System.arraycopy(chars, i * columns, result[i], 0, result[i].length);
}
return result;
}
/**
* concatenate two arrays after left shifting in loop
* @param before the first array in concat
* @param after the second array in concat
* @return concat
*/
public static char[] concat(char[] before, char[] after) {
return (String.valueOf(before) + String.valueOf(after))
.toCharArray();
}
/**
* Get file byte array
* @param file file
* @return Byte array
*/
public static byte[] getBytes(File file){
byte[] buffer = null;
FileInputStream fis = null;
ByteArrayOutputStream bos = null;
try {
fis = new FileInputStream(file);
bos = new ByteArrayOutputStream(1000);
byte[] b = new byte[1000];
int n;
while ((n = fis.read(b)) != -1) {
bos.write(b, 0, n);
}
buffer = bos.toByteArray();
} catch (IOException e) {
e.printStackTrace();
}finally {
try {
if (fis != null) {
fis.close();
}
} catch (IOException e) {
e.printStackTrace();
}finally {
if (bos != null) {
try {
bos.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
}
return buffer;
}
}
Base64 tool class
package com.hbh.AESTest.util;
import java.util.Base64;
/**
* @program: java_basis
* @description: Convert invisible characters to visible characters through Base64 encoding rules
* @author: hbh
* @create: 2022-02-05 16:55
*/
public class Base64Util {
/**
* Encoding byte arrays (AES)
* encode byte array
* @param bytes byte array
* @return encoded string
*/
public static String encode(byte[] bytes) {
return Base64.getEncoder().encodeToString(bytes);
}
/**
* Decodes a Base64 encoded string into a short array (AES)
* decode a encoded string to short array
* @param encodedText encoded text
* @return short array
*/
public static short[] decodeToShorts(String encodedText) {
return ArrayUtil.byteToShorts(Base64.getDecoder().decode(encodedText));
}
/**
* encode encrypted text bits by Base64 for processing unprintable (DES)
* and invisible character
* @param chars encrypted text bits
* @return encoded text
*/
public static String encode(char[] chars) {
char[][] segmentedChars = ArrayUtil.segmentDimension(chars, chars.length / 8, 8);
byte[] bytes = new byte[0];
for (char[] segmentedChar : segmentedChars) {
bytes = ArrayUtil.concat(bytes, ArrayUtil.int2Bytes(
Integer.parseInt(String.valueOf(segmentedChar), 2)));
}
return Base64.getEncoder().encodeToString(bytes);
}
/**
* decode decoded encrypted text bits in chars format (DES)
* @param encodedText encoded text
* @return encrypted text bits in chars format
*/
public static char[] decodeToChars(String encodedText) {
return ArrayUtil.bytesToChars(Base64.getDecoder().decode(encodedText));
}
/**
* Encoding unprocessed strings with Base64 (RC4)
* @param rawString Unprocessed string
* @return Encoded string
*/
public static String encode(String rawString) {
char[] chars = rawString.toCharArray();
byte[] bytes = new byte[0];
for (char c : chars) {
bytes = ArrayUtil.concat(bytes, ArrayUtil.int2Bytes(c));
}
return Base64.getEncoder().encodeToString(bytes);
}
/**
* Decode a Base64 encoded string (RC4)
* @param encodedText Base64 encoded string
* @return Decoding result
*/
public static String decode(String encodedText) {
StringBuilder builder = new StringBuilder();
byte[] bytes = Base64.getDecoder().decode(encodedText);
for (byte b : bytes) {
builder.append((char) (b & 0xff));
}
return builder.toString();
}
}
Reference articles
- https://blog.csdn.net/chengqiuming/article/details/82390910
- https://www.cnblogs.com/yanzi-meng/p/9640578.html
- https://blog.csdn.net/chengqiuming/article/details/82355772
- https://blog.csdn.net/qq_36949163/article/details/120932187
- https://blog.csdn.net/qq_28205153/article/details/55798628
- https://blog.csdn.net/chengqiuming/article/details/82429227