Demo 1: GA
Find the maximum of the following functions
f
(
x
)
=
sin
x
x
×
sin
y
y
,
−
10
≤
x
,
y
≤
10
f(x)=\frac{\sin x}{x}\times \frac{\sin y}{y}, -10\leq x, y\leq 10
f(x)=xsinx×ysiny,−10≤x,y≤10
Code
function [max_x, max_fval] = MLYGA2(func, LB, UB, popsize, iter_max, px, pm, esp)
%func: Objective function to be optimized
% LB: Lower bound of independent variable
% UB: Upper bound of independent variable
% popsize: Population size
% iter_max: Maximum number of iterations
% px: Crossover probability
% pm: Variation probability
% epsl: Discrete precision of independent variable
if isempty(pm)
pm=0.1;
end
if isempty(px)
px=0.90;
end
if isempty(iter_max)
iter_max=8000;
end
if isempty(popsize)
popsize=50;
end
if isempty(LB) && isempty(UB)
nvar = input('Please enter the number of variables nvar=');
else
nvar = size(LB, 1);
end
CodeLen = nvar*max(ceil(log2((UB-LB)/esp+1))); % According to the discrete precision of independent variables, the length of binary coding string is determined
x = zeros(popsize, CodeLen); % Initial value of population code
for i=1:popsize
x(i, :)=init(CodeLen); % Call subroutine to initialize population
FitValue(i) = func(Decl(LB, UB, x(i, :), CodeLen)); % Calculate individual fitness
end
for j=1:iter_max
SumFitValue = sum(FitValue); % Sum of fitness values of all individuals
Ave_x = FitValue/SumFitValue;
Prob_Ave_x=0;
Prob_Ave_x(1)=Ave_x(1);
for i=2:popsize
Prob_Ave_x(i)=Prob_Ave_x(i-1)+Ave_x(i);
end
% operators
% FaSelection = 1; % Set default values
for k=1:popsize
rd = rand;
for n=1:popsize
if rd<=Prob_Ave_x(n)
FaSelection = n; % Select the parent by roulette strategy
break;
end
end
MoSelection=floor(rand() * (popsize-1))+1; % Randomly determine the mother generation
PosCrossover = floor(rand() * (CodeLen-2))+1; % Randomly determine the location of the intersection
r1 = rand;
% Cross operation occurs
if r1<=px
nx(k, 1:PosCrossover) = x(FaSelection, 1:PosCrossover);
nx(k, (PosCrossover+1):CodeLen) = x(MoSelection, (PosCrossover+1):CodeLen);
r2 = rand;
% Perform mutation operation
if r2<=pm
PosMutation = round(rand()*(CodeLen-1)+1); % Location of variant elements
nx(k, PosMutation) = ~nx(k, PosMutation);
end
% Otherwise, directly inherit the parent
else
nx(k, :)=x(FaSelection, :);
end
end
x = nx;
for m=1:popsize
% Calculate fitness function value
FitValue(m)=func(Decl(LB, UB, x(m, :), CodeLen));
end
[~, index]=max(FitValue); % The objective function is to find the maximum value
best = x(index, :);
x(popsize, :)=best;
end
max_x = Decl(LB, UB, best, CodeLen);
max_fval = func(max_x);
end
% Initialization function, Binary encoding
function y = init(L)
for i=1:L
y(i) = round(rand());
end
end
% Binary code back to decimal code
function y=Decl(LB, UB, x, CodeLen)
nvar = size(LB, 1);
sublen = CodeLen/nvar;
bit_w = 2.^(0:sublen); % Calculate bit weight
maxintval = 2^sublen-1;
range = UB'-LB';
start = 1;
fin = sublen;
for j = 1:nvar
tvars(1:sublen)=x(start:fin);
start = start+sublen;
fin = fin+sublen;
t_sum = 0;
for k=1:sublen
t_sum = t_sum+bit_w(k)*tvars(sublen-k+1);
end
y(j)=(range(j)*(t_sum/maxintval))+LB(j);
end
end
Demo2: GA
Using binary coding, write GA algorithm to solve
function [max_x, max_fval] = MLYGA2(func, LB, UB, popsize, iter_max, px, pm, esp)
%func: Objective function to be optimized
% LB: Lower bound of independent variable
% UB: Upper bound of independent variable
% popsize: Population size
% iter_max: Maximum number of iterations
% px: Crossover probability
% pm: Variation probability
% epsl: Discrete precision of independent variable
if isempty(pm)
pm=0.1;
end
if isempty(px)
px=0.90;
end
if isempty(iter_max)
iter_max=8000;
end
if isempty(popsize)
popsize=50;
end
if isempty(LB) && isempty(UB)
nvar = input('Please enter the number of variables nvar=');
else
nvar = size(LB, 1);
end
global fitall
fitall = zeros(1, iter_max);
CodeLen = nvar*max(ceil(log2((UB-LB)/esp+1))); % According to the discrete precision of independent variables, the length of binary coding string is determined
x = zeros(popsize, CodeLen); % Initial value of population code
for i=1:popsize
x(i, :)=init(CodeLen); % Call subroutine to initialize population
FitValue(i) = func(Decl(LB, UB, x(i, :), CodeLen)); % Calculate individual fitness
end
for j=1:iter_max
SumFitValue = sum(FitValue); % Sum of fitness values of all individuals
Ave_x = FitValue/SumFitValue;
Prob_Ave_x=0;
Prob_Ave_x(1)=Ave_x(1);
for i=2:popsize
Prob_Ave_x(i)=Prob_Ave_x(i-1)+Ave_x(i);
end
% operators
% FaSelection = 1; % Set default values
for k=1:popsize
rd = rand;
for n=1:popsize
if rd<=Prob_Ave_x(n)
FaSelection = n; % Select the parent by roulette strategy
break;
end
end
MoSelection=floor(rand() * (popsize-1))+1; % Randomly determine the mother generation
PosCrossover = floor(rand() * (CodeLen-2))+1; % Randomly determine the location of the intersection
r1 = rand;
% Cross operation occurs
if r1<=px
nx(k, 1:PosCrossover) = x(FaSelection, 1:PosCrossover);
nx(k, (PosCrossover+1):CodeLen) = x(MoSelection, (PosCrossover+1):CodeLen);
r2 = rand;
% Perform mutation operation
if r2<=pm
PosMutation = round(rand()*(CodeLen-1)+1); % Location of variant elements
nx(k, PosMutation) = ~nx(k, PosMutation);
end
% Otherwise, directly inherit the parent
else
nx(k, :)=x(FaSelection, :);
end
end
x = nx;
for m=1:popsize
% Calculate fitness function value
FitValue(m)=func(Decl(LB, UB, x(m, :), CodeLen));
end
[bestV, index]=max(FitValue); % The objective function is to find the maximum value
best = x(index, :);
x(popsize, :)=best;
fitall(j)=bestV;
end
max_x = Decl(LB, UB, best, CodeLen);
max_fval = func(max_x);
end
% Initialization function, Binary encoding
function y = init(L)
for i=1:L
y(i) = round(rand());
end
end
% Binary code back to decimal code
function y=Decl(LB, UB, x, CodeLen)
nvar = size(LB, 1);
sublen = CodeLen/nvar;
bit_w = 2.^(0:sublen); % Calculate bit weight
maxintval = 2^sublen-1;
range = UB'-LB';
start = 1;
fin = sublen;
for j = 1:nvar
tvars(1:sublen)=x(start:fin);
start = start+sublen;
fin = fin+sublen;
t_sum = 0;
for k=1:sublen
t_sum = t_sum+bit_w(k)*tvars(sublen-k+1);
end
y(j)=(range(j)*(t_sum/maxintval))+LB(j);
end
end
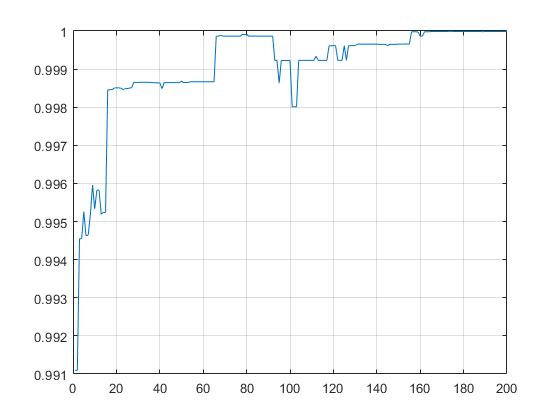
Use the GA toolbox of MATLAB to solve
% Use your own GA Toolbox solution
global fitall_ga;
fitall_ga = zeros(1, Ngen);
% ops = optimoptions('ga', 'Generations', Ngen, 'PlotFcn', @gaplotbestf);
ops = optimoptions('ga', 'Generations', Ngen, 'OutputFcn', @myout, 'CrossoverFraction', 0.2);
[max_x_ga, maxfval_ga, ~, output, population, scores] = ga(@obj_func_3x, 2, [], [], [], [], LB, UB, [], ops);
plot(1:output.generations, -fitall_ga(:, 1:output.generations));
grid on;
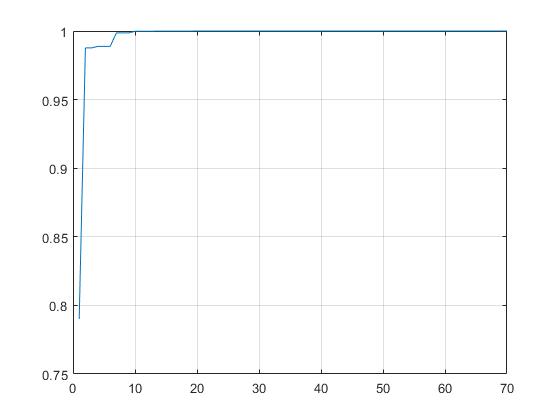
Demo3: GA
Solve the minimum of the following functions
f
(
x
)
=
−
x
2
+
2
x
+
0.5
,
−
10
≤
x
,
y
≤
10
f(x)=-x^2+2x+0.5, -10\leq x, y\leq 10
f(x)=−x2+2x+0.5,−10≤x,y≤10
Main function
%% [MinValue, MinFunc]=MLYGA3(@obj_func_3r, -10, 10, 0.001); % GA Toolbox solution [x_ga, MinFunc_ga, ~, output, population, scores] = ga(@obj_func_3r, 1, [], [], [], [], -10, 10);
Real coded GA solution
function [MinValue, MinFunc] = MLYGA3(func, LB, UB, eps)
%eps For accuracy
n = ceil(log2((UB-LB)/eps+1));
individual = {};
for i=1:n
individual = [individual; [0 1]];
end
individualCode = exhaus(individual); % Enumerate all possible permutations
% Decimal number corresponding to chromosome code
individualCodeValue = zeros(1, 2^n);
for i=1:2^n
for j=1:n
individualCodeValue(i)=individualCodeValue(i)+individualCode(i, j)*2^(n-j);
end
end
% The chromosome code corresponds to the real number of a given domain( real-code)
CodeValue=zeros(1, 2^n);
for k=1:2^n
CodeValue(k)=CodeValue(k)+LB+individualCodeValue(k)*(UB-LB)/(2^n-1);
end
% Always make the first value the minimum
MinFunc=func(CodeValue(1));
MinIndividual = individualCode(1);
MinValue = CodeValue(1);
for i=2:2^n
FuncValue(i)=func(CodeValue(i));
if FuncValue(i)<MinFunc
MinFunc=FuncValue(i);
MinIndividual = individualCode(i);
MinValue = CodeValue(i);
end
end
end
Demo4: EP
Solve using evolutionary computation
f
i
(
x
)
=
∑
i
=
1
n
[
x
i
2
−
10
cos
(
2
π
x
i
)
+
10
]
,
∣
x
i
∣
≤
5.12
f_i(x)=\sum_{i=1}^n[x_i^2-10\cos(2\pi x_i)+10], |x_i|\leq 5.12
fi(x)=i=1∑n[xi2−10cos(2πxi)+10],∣xi∣≤5.12
Different from the starting point of genetic algorithm, evolutionary programming simulates the evolutionary process of organisms from the perspective of the whole. In evolutionary programming, crossover and other individual recombination operators are not used. Therefore, in evolutionary programming, individual mutation operation is the only individual optimal search method Gaussian mutation operator obtains the standard deviation of individual mutation by calculating the square root of the linear transformation of the fitness function value of each individual in the process of mutation
σ
i
\sigma_i
σ i, and add a random number subject to normal distribution to each component
X
(
t
+
1
)
=
X
(
t
)
+
N
(
0
,
σ
)
σ
(
t
+
1
)
=
β
F
(
X
(
t
)
)
+
γ
x
i
(
t
+
1
)
=
x
i
(
t
)
+
N
(
0
,
σ
(
t
+
1
)
)
\begin{aligned} &X(t+1)=X(t)+N(0, \sigma)\\ &\sigma(t+1)=\sqrt{\beta F(X(t))+\gamma}\\ &x_i(t+1)=x_i(t)+N(0, \sigma(t+1)) \end{aligned}
X(t+1)=X(t)+N(0,σ)σ(t+1)=βF(X(t))+γ
xi(t+1)=xi(t)+N(0,σ(t+1))
EP
In evolutionary programming, the selection operation is carried out from the parents and offspring according to the fitness function value in a way of random competition 2 N 2N Select from 2N individuals N N N better individuals form the next generation population. There are three selection methods: probability selection, tournament selection and elite selection. The commonly used ones are tournament selection:
- take N N The population composed of N parent individuals and the population obtained after one mutation operation N N N offspring individuals are merged to form a Co containing 2 N 2N Set of 2N individuals I I I.
- For each individual x i ∈ I x_i\in I xi ∈ I, from I I Random selection in I q q q individuals, and q q Fitness function value of q individuals and x i x_i Compare the fitness function of xi ， and calculate this q ( q ≥ 1 ) q(q\geq 1) Fitness function value ratio in q(q ≥ 1) individuals x i x_i xi. Number of individuals with poor fitness w i w_i wi, and w i w_i wi as x i x_i xi)'s score
- At all 2 N 2N 2N individuals are compared and scored according to each individual w i w_i wi ， sort and select N N N individuals with the highest score are regarded as the next generation population
As you can see, q q q value is the key to the selection of operator q q When the q value is large, the operator tends to deterministic selection; When q = 2 N q=2N When q=2N, the operator determines from 2 N 2N Select from 2N individuals N N N individuals with high fitness are prone to premature and other disadvantages And when q q When the value of q is small, the operator tends to random selection, which reduces the control ability of fitness, resulting in the selection of a large number of individuals with low fitness, resulting in population degradation
CEP
Adaptive standard evolutionary programming algorithm
- Randomly generated by μ \mu μ A population composed of individuals and set k = 1 k=1 k=1, each individual uses a real number pair ( x i , η i ) , ∀ i ∈ { 1 , 2 , ... , μ } (x_i, \eta_i), \forall i\in\{1,2,\dots, \mu\} (xi, η i),∀i∈{1,2,…, μ} Means, where x i x_i xi is the target variable, η i \eta_i η i ， is the standard deviation of normal distribution
- Calculate the fitness function value of each individual in the population about the objective function. In solving the problem of function minimization, the fitness function value is the objective function value f ( x i ) f(x_i) f(xi).
- For each individual
(
x
i
,
η
i
)
(x_i, \eta_i)
(xi, η i) produce unique offspring by the following methods:
(
x
i
′
,
η
i
′
)
(x_i',\eta_i')
(xi′,ηi′).
x i ′ ( j ) = x i ( j ) + η i ( j ) N j ( 0 , 1 ) η i ′ = η i ( j ) exp ( τ ′ N ( 0 , 1 ) + τ N j ( 0 , 1 ) ) \begin{aligned} &x_i'(j)=x_i(j)+\eta_i(j)N_j(0, 1)\\ &\eta'_i=\eta_i(j)\exp(\tau'N(0, 1)+\tau N_j(0, 1)) \end{aligned} xi′(j)=xi(j)+ηi(j)Nj(0,1)ηi′=ηi(j)exp(τ′N(0,1)+τNj(0,1))
SPMEP
The single point mutation algorithm improves the individual mutation method based on CEP algorithm. In each iteration, only one component of each parent individual is mutated, which improves the computational efficiency In SPMEP algorithm, the generation method of offspring is
x
i
′
(
j
i
)
=
x
i
(
j
i
)
+
η
i
N
i
(
0
,
1
)
η
i
′
(
j
)
=
η
i
(
j
)
exp
(
−
α
)
\begin{aligned} &x'_i(j_i)=x_i(j_i)+\eta_iN_i(0, 1)\\ &\eta'_i(j)=\eta_i(j)\exp(-\alpha) \end{aligned}
xi′(ji)=xi(ji)+ηiNi(0,1)ηi′(j)=ηi(j)exp(−α)
among
α
=
1.01
\alpha=1.01
α= 1.01. SPMEP algorithm has obvious advantages in solving high-dimensional multimode function problems, and the algorithm also has good stability
Compare the solution of evolutionary algorithm and GA
function [minx, minf]=MLYEP(func, popsize, iter_max, LB, UB, type)
global fitall
nvar = size(LB, 1); % Get the number of variables
tau1=sqrt(2*nvar)^(-1); % CEP Evolutionary parameters in t1
tau2=sqrt(2*sqrt(nvar))^(-1); % CEP Evolutionary parameters in t2
q = round(0.9*popsize); % q The setting of the value shall be considered 90 at a time%Individual population
chome=zeros(popsize, nvar);
for i=1:popsize
for j=1:nvar
chome(:, j)=unifrnd(LB(j), UB(j), popsize, 1); % initialization
chomeLambda(j)=(UB(j)-LB(j))/2;
chomeVar(j)=var(chome(:, j));
end
chomeV(i, 1)=func(chome(i, :)); % Calculate fitness
chomeSigma(i, 1)=sqrt(chomeV(i, 1));
end
[a, b]=sort(chomeV);
chome=chome(b, :);
chomeV=chomeV(b);
chomeSigma=chomeSigma(b);
minx=chome(1, :);
minf=chomeV(1);
for i=1:iter_max
if type==1 % standard
for j=1:popsize
for k=1:nvar
newchome(j, k)=chome(j, k)+normrnd(0, chomeSigma(k), 1, 1);
newchome(j, k)=boundtest(newchome(j, k), LB(k), UB(k)); % Perform boundary detection
end
end
elseif type==2 % self-adaption, Use a pair of real pairs to represent individuals
for j=1:popsize
a = randn;
for k=1:nvar
newchome(j, k)=chome(j, k)+randn*chomeVar(k);
newchome(j, k)=boundtest(newchome(j, k), LB(k), UB(k));
chomeVar(k)=chomeVar(k)*exp(tau1*a+tau2*randn);
end
end
elseif type==3 % Single point variation
for j=1:popsize
b1 = ceil(nvar*rand);
if chomeLambda(b1)<1e-4
chomeLambda(b1)=(UB(b1)-LB(b1))/2;
end
newchome(j, b1)=chome(j, b1)+chomeLambda(b1)*randn;
newchome(j, b1)=boundtest(newchome(j, b1), LB(b1), UB(b1));
chomeLambda(b1)=chomeLambda(b1)*exp(-1.01);
end
end
for j=1:popsize
newchomeV(j, 1)=func(newchome(j, :));
end
chome=EPSelect(chome, newchome, chomeV, newchomeV, q); % Select offspring
for j=1:popsize
chomeV(j, 1)=func(chome(j, :));
chomeSigma(j, 1)=sqrt(chomeV(j, 1));
end
[~, b]=sort(chomeV); % Sort according to fitness value
chome=chome(b, :);
chomeV = chomeV(b);
chomeSigma = chomeSigma(b);
if minf>chomeV(1)
minx=chome(1, :);
minf=chomeV(1);
end
fitall(i)=minf;
end
end
% Selection operator
function chome=EPSelect(old, new, oldF, newF, q)
num=size(old, 1);
total_chome=[old; new]; % Merge parents and children
total_F = [oldF; newF]; % Combining fitness functions of parents and children
competitor = randperm(2*num);
for i=1:2*num
score = 0;
for j=1:q
if total_F(i)<total_F(competitor(j))
score = score+1;
end
end
templ(i)=score;
end
[~, b]=sort(templ, 'descend');
total_chome=total_chome(b, :);
chome=total_chome(1:num, :);
end
function y=boundtest(x, LB, UB)
if x>=UB
y=LB+(x-UB);
elseif x<=LB
y=UB-(LB-x);
else
y=x;
end
end
SPMEP fitness curve (EP and CEP fall into local optimization)
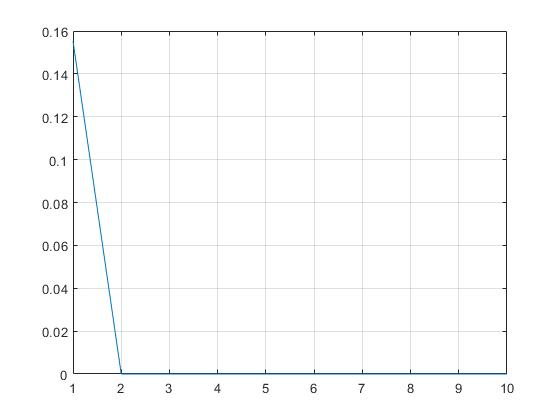GA toolbox solution
%% GA solve
global fitall_ga;
fitall_ga = zeros(1, iter_max);
ops = optimoptions('ga', 'Generations', iter_max, 'OutputFcn', @myout);
[minx_ga, minf_ga, ~, output, population, scores]=ga(@obj_func_7x, 10, [], [], [], [], LB, UB,[],ops);
plot(1:output.generations, fitall_ga(:, 1:output.generations));
grid on;
Reference
Optimization method and its Matlab implementation