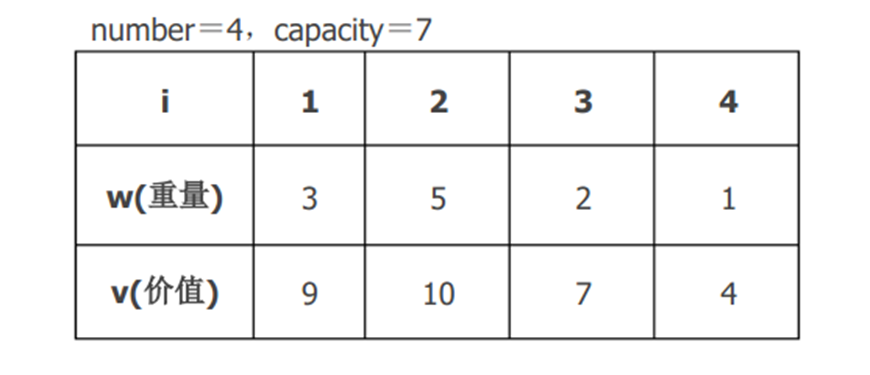
Given n items and a backpack. The weight of item i is wi > 0, its value is VI > 0, and the capacity of the backpack is c. How to select the items to be loaded into the backpack to maximize the total value of the items loaded into the backpack? (backtracking is required)

Steps:

1. Enter the item quantity n;
2. Input the weight wi and value vi of the item in turn;
3. Sort the items according to their unit weight value from large to small;
4. Construct a subset tree of solutions. For each item i, there are only two decisions to choose or not to choose for the item. There are n items in total. Each item is considered in order, so a solution space tree is formed. The basic idea is to traverse the tree to enumerate all cases, and finally make a judgment. If the weight does not exceed the backpack capacity and the value is the largest, this scheme is the final answer.
5. In the recursive function Backtrack, when I > N, the algorithm searches the leaf node to get a new item packaging scheme. At this time, the algorithm updates the current optimal value in time. When I < n, the current expansion node is located in the (i-1) layer of the arrangement tree. At this time, the algorithm selects the next item to be arranged, recursively searches the corresponding subtree in the way of depth first, and cuts the corresponding subtree for the node that does not meet the upper bound constraint.
6. When searching the state space tree, as long as the left child node is a feasible node, the search will enter its left child tree. For the right subtree, the upper bound function is calculated to judge whether to prune it.

Experimental principle:

Backtracking method is a very effective method, known as "general problem-solving method". It is a bit like exhaustive method, but it is more jumping and systematic. It can systematically search all solutions and any solution of a problem. The backtracking method adopts the depth first strategy.

The backtracking method searches the solution space tree of the problem according to the depth first strategy. Firstly, the solution space tree is searched from the root node. When the algorithm searches a node of the solution space tree, the pruning function is used to judge whether the node is feasible (that is, the solution of the problem can be obtained). If it is not feasible, skip the search of the subtree with the node as the root and trace back to its ancestor node layer by layer; Otherwise, enter the subtree and continue to search according to the depth first strategy.

Test procedure:
knapsack algorithm
Compared with implementation 1, this algorithm effectively avoids unnecessary and comparison process. When J < w [i], m[i+1][j] is directly filled without comparison. In addition, since the first c-1 data of the last line is not used, there is no need to calculate.

int knapsack(int m[][maxn],int n,int c)
{
    int jMax=min(w[n],c);
    //In the first row of pretreatment, j is less than w[n], the filler is 0, otherwise the filler is v[n]
    for(int j=0;j<jMax;j++) m[n][j]=0;
    for(int j=jMax;j<c;j++) m[n][j]=v[n];
    for(int i=n-1;i>1;i--)//The last line is not calculated because some of the padding is invalid
    {
        jMax=min(w[i],c);
        for(int j=0;j<jMax;j++)
            m[i][j]=m[i+1][j];//Not selected
        for(int j=jMax;j<c+1;j++)
            m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
    }
    m[1][c]=max(m[2][c],m[2][c-w[1]]+v[1]);//Process the last data of the last row
    return m[1][c];
}   

The selection method for solving the optimal solution traceBack backtracking
After forming the above set of tables, we can easily get the optimal solution m[1][c], but how to solve the selection method? We can still use recursive backtracking:

If m[i][c]==m[i+1][c], item I is not selected, I++
If m[i][c]= M [i + 1] [C], indicating that item I is selected, i++,c-wi
When i=n, if m[n][c]= 0 indicates that item n is selected, otherwise it is not selected

void traceBack(int m[maxn][maxn],int w[],int c,int n,int x[])
{
    for(int i=1;i<n;i++)
    {
        if(m[i][c]==m[i+1][c]) x[i]=0;
        else{
            x[i]=1;
            c-=w[i];
        }
    }
    x[n]=(m[n][c])?1:0;
}	    

Total code:

#include <iostream>
#include <stdlib.h>
using namespace std;
const int maxn=1005;
int m[maxn][maxn]={0};
int w[maxn]={0};
int v[maxn]={0};
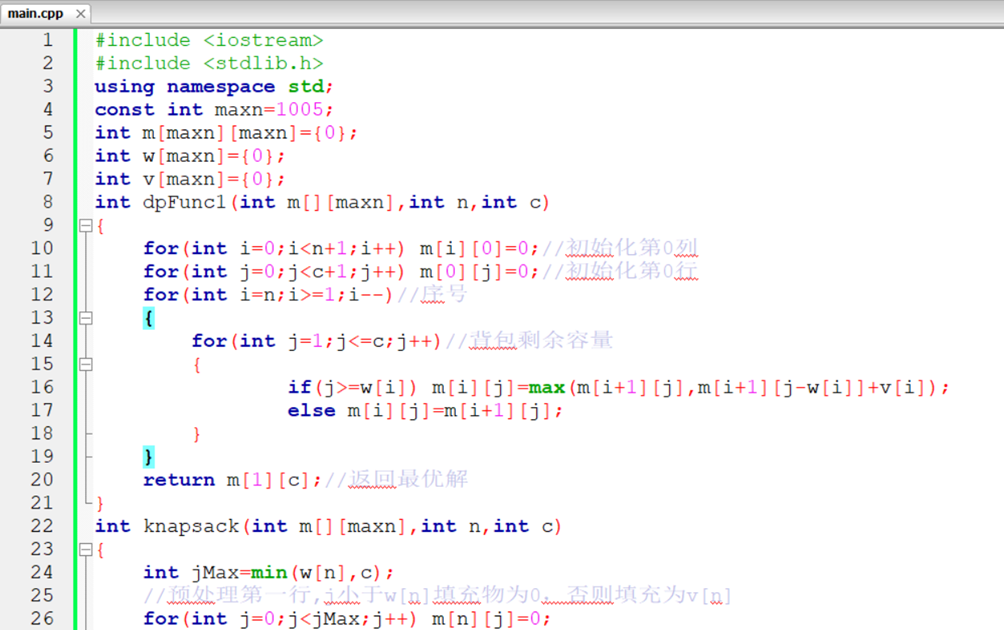
int dpFunc1(int m[][maxn],int n,int c)
{
    for(int i=0;i<n+1;i++) m[i][0]=0;//Initialize column 0
    for(int j=0;j<c+1;j++) m[0][j]=0;//Initialize line 0
    for(int i=n;i>=1;i--)//Serial number
    {
        for(int j=1;j<=c;j++)//Remaining capacity of backpack
        {
                if(j>=w[i]) m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
                else m[i][j]=m[i+1][j];
        }
    }
    return m[1][c];//Return to optimal solution
}
int knapsack(int m[][maxn],int n,int c)
{
    int jMax=min(w[n],c);
    //In the first row of pretreatment, j is less than w[n], the filler is 0, otherwise the filler is v[n]
    for(int j=0;j<jMax;j++) m[n][j]=0;
    for(int j=jMax;j<c;j++) m[n][j]=v[n];
    for(int i=n-1;i>1;i--)//The last line is not calculated because some of the padding is invalid
    {
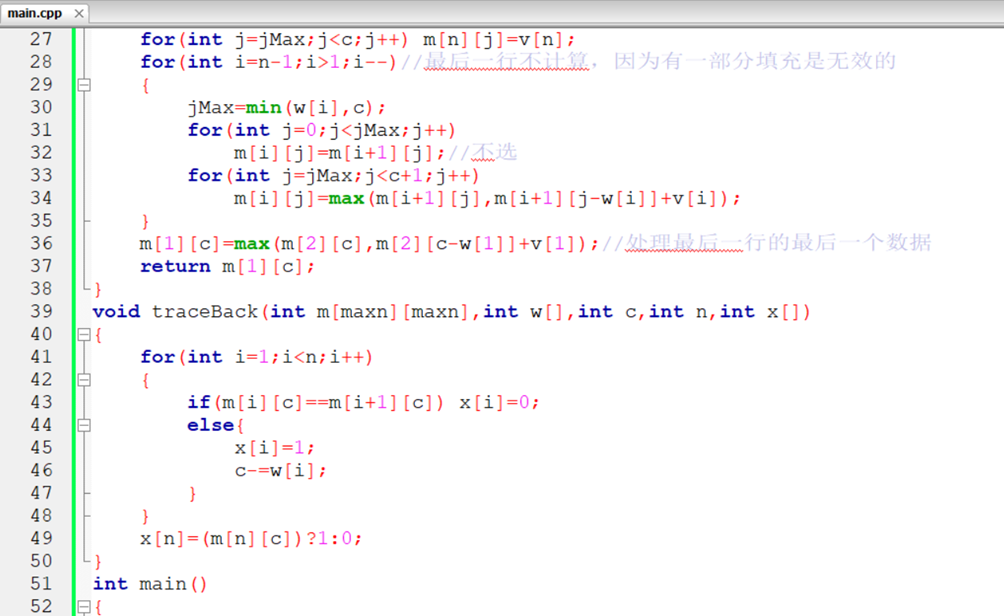
        jMax=min(w[i],c);
        for(int j=0;j<jMax;j++)
            m[i][j]=m[i+1][j];//Not selected
        for(int j=jMax;j<c+1;j++)
            m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
    }
    m[1][c]=max(m[2][c],m[2][c-w[1]]+v[1]);//Process the last data of the last row
    return m[1][c];
}
void traceBack(int m[maxn][maxn],int w[],int c,int n,int x[])
{
    for(int i=1;i<n;i++)
    {
        if(m[i][c]==m[i+1][c]) x[i]=0;
        else{
            x[i]=1;
            c-=w[i];
        }
    }
    x[n]=(m[n][c])?1:0;
}
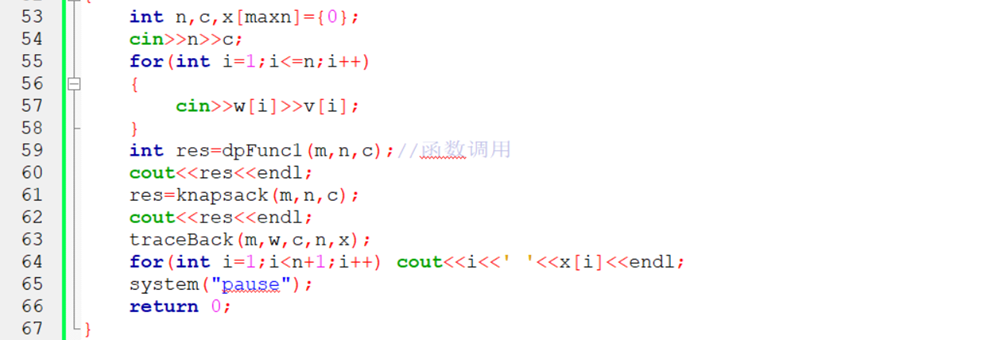
int main()
{
    int n,c,x[maxn]={0};
    cin>>n>>c;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
    }
    int res=dpFunc1(m,n,c);//function call
    cout<<res<<endl;
    res=knapsack(m,n,c);
    cout<<res<<endl;
    traceBack(m,w,c,n,x);
    for(int i=1;i<n+1;i++) cout<<i<<' '<<x[i]<<endl;
    system("pause");
    return 0;
}

Experimental test:

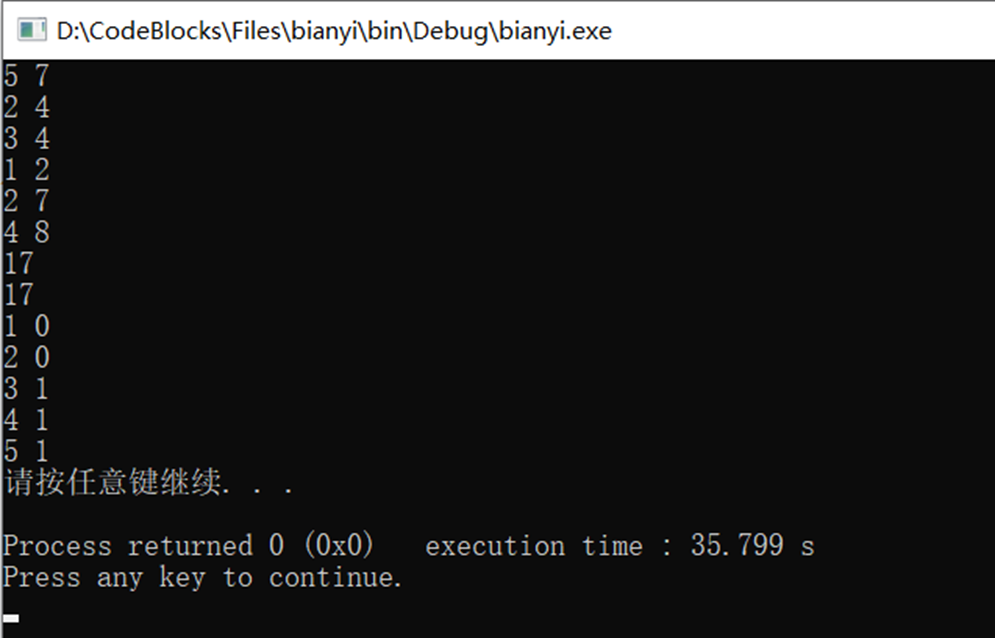
Complexity analysis:

Time complexity: T(n)=O(n^2)
Space complexity: S(n)=O(n^2)