1, Experimental purpose
1. Be familiar with the integrated development environment of C/C + + language;
2. Master the concept of algorithm;
3. Understand the problem solving method;
4. Understand the idea of recursion and learn to write recursion.
2, Experimental principle
- algorithm
An algorithm is a description of the steps of solving a specific problem. It is a finite sequence of instructions. The algorithm has the following five characteristics: input; output; Certainty; effectiveness; finiteness. - Problem solving process
understand the problem;
devise a plan;
Carry out the plan;
look back. - recursive
Recursive definition is a definition method that directly or indirectly refers to itself. A legal recursive definition includes two parts: base case and recursive part. The basic situation clearly lists several simple objects of new things in direct form, and the recursive part gives the conditions and methods for defining new objects from simple (or relatively simple) objects.
3, Experimental content
Counterfeit money problem
Description:
Sally has 12 silver coins. There are 11 real coins and one counterfeit. Counterfeit money looks no different from real money, but its weight is different. But Sally didn't know whether counterfeit money was lighter or heavier than real money. So he borrowed a balance from his friend. Friends hope Sally can find the counterfeit money three times and determine whether the counterfeit money is light or heavy. for example:If you use the balance to weigh two coins and find that the balance is balanced, it means that both coins are true. If the match uses a real coin to compare with another silver coin and finds that it is lighter or heavier than the real coin, it indicates that it is a counterfeit coin. After carefully arranging each weighing, Sally promised to determine the counterfeit money after weighing it three times.
Input:
The first line has a number n,Indicates yes n Group test cases.
For each set of test cases:
There are three lines of input, and each line represents the result of one weighing. Sally marked the silver coin as A-L. The results of each weighing are represented by three strings separated by spaces: the coins placed on the left of the balance and the coins placed on the right of the balance. Wherein, the equilibrium state is``up'', ``down'', or ``even''express, They are right end high, right end low and balance respectively. The number of coins on the left and right of the balance is always equal.
Output:
Output which label of silver coin is counterfeit, and indicate whether it is lighter or heavier than real coin(heavy or light).
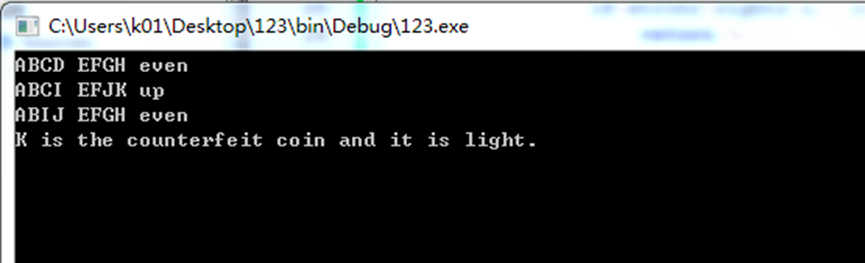
Sample input:
1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
Sample output:
K is the counterfeit coin and it is light.
Problem solving ideas:
-
The sample input has three lines of data, each line of data has three strings, and the length of each string is no more than 6 (up to 6 silver coins on the left and right sides). Therefore, first set three arrays to store the input data, namely left[3][7], right [3] [7], and result [3] [7]. So,
left[0]=ABCD, right[0]=EFGH, result[0]= even
left[1]= ABCI, right[1]= EFJK, result[1]= up
left[2]= ABIJ, right[2]= EFGH, result[2]= even -
How to express the weight of silver coins? The 12 silver coins are ABCDEF L indicates that A is the first silver coin, B is the second silver coin,... L is the 12th silver coin. Suppose to use the array status to store the silver coin weight:
A ------> status[0]
B ------> status[1]
C ------> status[2]
D ------> status[3]
...
L ------> status[12]First assign the weight of 12 silver coins
for(i=0;i<12;i++) status[i]=0
There are two cases for each gold coin, so the enumeration method is adopted, and the variables are the number x and weight of each gold coin. In all 24 possible guesses, enumerate each gold coin and its weight. When all conditions are met, it is assumed to be true.
for(i=0;i<12;i++)
Suppose the weight of light silver coins is - 1 status[i]=-1;if (isBalance()) break;
Suppose the weight of the heavy silver coin is 1; status[i]=1; if (isBalance()) break;
Suppose the weight of normal silver coin is 0, status [i] = 0;
- ABCD EFGH even: put four silver coins of ABCD on the left and four silver coins of EFGH on the right of the balance. The status is even; That is, left = the weight of a silver coin + the weight of B silver coin + the weight of C silver coin + the weight of D silver coin, right = the weight of e silver coin + the weight of F silver coin + the weight of G silver coin + the weight of H silver coin. Bring in the weight of silver coins to judge whether the conditions are met. If true is output, otherwise false is output.
bool isBalance()
{
for(i=0;i<3;i++)
{
leftw=rightw=0;
for(j=0;j<6 && left[i][j]!=0;j++)
{
leftw+=status[left[i][j]-'A'];
rightw+=status[right[i][j]-'A'];
}
If (leftw== rightw && result[i][0]!='e')
return false;
If (leftw> rightw && result[i][0]!='u')
return false;
If (leftw< rightw && result[i][0]!='d')
return false;
}
return true;
}
Problem analysis:
According to the given conditions, it is difficult to get the required answer by marking the weight of silver coins correctly.
Violence laws are necessary. 12 silver coins are A-L, so A-L may be heavy or light. There are 24 cases. Just try them respectively.
code:
#include <stdio.h>
#include <string.h>
#define N 3
#define M 8
char left2[N][M], right2[N][M], result[N][M];
int judge(char c, int heavy)
{
int i;
for(i = 0; i < N; i++) {
if(result[i][0] == 'e') {
if(strchr(left2[i], c) != NULL || strchr(right2[i], c) != NULL)
return 0;
} else if(result[i][0] == 'u') {
if(heavy) {
if(strchr(left2[i], c) == NULL)
return 0;
} else {
if(strchr(right2[i], c) == NULL)
return 0;
}
} else if(result[i][0] == 'd') {
if(heavy) {
if(strchr(right2[i], c) == NULL)
return 0;
} else {
if(strchr(left2[i], c) == NULL)
return 0;
}
}
}
return 1;
}
int main()
{
int n,i;
char c;
scanf("%d", &n);
while(n--) {
for(i = 0; i < N; i++)
scanf("%s%s%s", left2[i], right2[i], result[i]);
for(c = 'A'; c <= 'L'; c++) {
if(judge(c, 1)) {
printf("%c is the counterfeit coin and it is heavy.\n", c);
break;
}
if(judge(c, 0)) {
printf("%c is the counterfeit coin and it is light.\n", c);
break;
}
}
}
return 0;
}
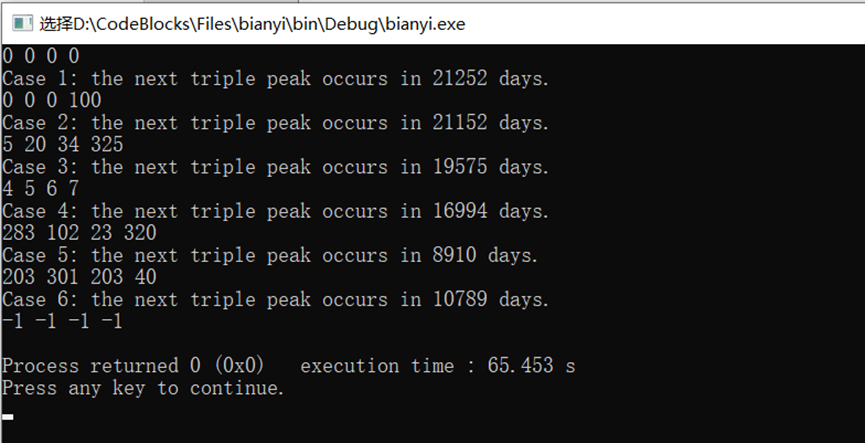
Compilation execution:
function:
4148: physiological cycle
Description:
There are three physiological cycles in human life, namely physical cycle, emotional cycle and intellectual cycle. Their cycle lengths are 23 days, 28 days and 33 days respectively. One day in each cycle is the peak. On the peak day, people will perform well in the corresponding aspects. For example, at the peak of the intelligence cycle, people will be quick thinking and easy to pay high attention. Because the lengths of the three cycles are different, the peaks of the three cycles usually do not fall on the same day. For everyone, want to know when the three peaks fall on the same day. For each cycle, the number of days from the first day of the current year to the peak (not necessarily the time of the first peak) will be given. Given a number of days from the first day of the year, your task is to output the time (days from the given time) when the next three peaks fall on the same day starting from the given time (excluding the given time). For example, if the given time is 10 and the time of the next three peaks on the same day is 12, 2 will be output (note that this is not 3).
Input:
The input contains multiple groups of data, each group of data is composed of four integers, and the data ends with - 1 - 1 - 1. For the four integers p, e, i and d, p, e, i respectively represent the time of physical strength, emotion and intelligence peak (the time is calculated from the first day of the year). d is a given time and may be less than p, e or i. All given times are nonnegative and less than or equal to 365, and the required time is less than or equal to 21252.
Output:
From the given time, the time of the next three peaks on the same day (days from the given time).
Sample input:
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
Sample output:
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.
Problem solving ideas:
It can be understood here that if the conditions are met on day n, the three cycles must have experienced N1, N2 and N3 cycles, plus the number of initialization days, which is equal to N, that is, assuming that the conditions are met on day 1024, there must be 1024=23n1+51024=28n2+201024=33*n3+34 for line 3 in the example, so as long as you judge, Whether this day meets the conditions: (D-5)% 23 = = 0 & & (D-20)% 28 = = 0 & & (d-34)% 33 = = 0, enumeration is enough.
code:
#include <iostream>
#include <vector>
#include <cmath>
#include <stdio.h>
using namespace std;
int main() {
int p, e, i;// I have three indicators p e i, which peak every other period of time. I ask which day the three indicators peak
int d; //Specify Date
int cnt = 1;
//23 28 33
while (cin >> p >> e >> i >> d) {
if (p == -1 && e == -1 && i == -1 && d == -1) {
return 0;
}
/*
Assuming that the day is k (traversing k: d+1 ~ 21252), the timing of the three peaks:
(k - p) % 23 == 0 // It is 23 days from the last peak, so today k is the peak of p index
(k - e) % 28 == 0 // It is 28 days from the last peak, so today k is the peak of e index
(k - i) % 33 == 0 // It is 33 days from the last peak, so today k is the peak of i index
*/
int k;
for (k = d + 1; (k - p) % 23 != 0; k ++); // Let k assign the first p peak
for (; (k - e) % 28 != 0; k += 23); // At this time k is double peak
for (; (k - i) % 33 != 0; k += 23 * 28); // Least common multiple of 23 * 28: 23 * 28
printf("Case %d: the next triple peak occurs in %d days.\n", cnt++, k - d);
}
return 0;
}
Compilation execution:
function: