Merge K sort lists

Merge k sorted lists to return the merged sorted list. Please analyze and describe the complexity of the algorithm.

Example:

Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1 - > 1 - > 2 - > 3 - > 4 - > 4 - > 5 - > 6

1. Violent solution

This solution is too violent, please use it carefully

The principle is to disassemble, sort and combine all nodes into a list, which is easy to understand

Time complexity is O(nlogn)

2. enumeration method

The main idea of this solution is to traverse the header values of all lists and push the smallest one into the current result queue

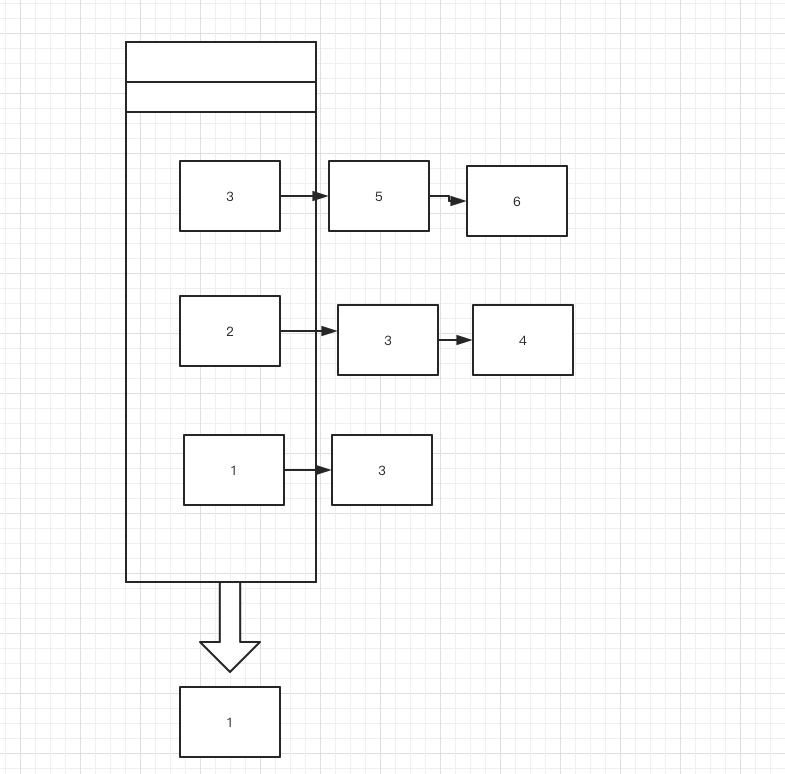
The specific solution is

var isOver = function (lists) {
    let r = true
    lists.map(val => {
        if (val) {
            r = false
            return r
        }
    })
    
    return r
}

var minNode = function (lists) {
    let val = null
    let j
    for (var i = 0; i < lists.length; i++) {
        if (lists[i]) {
            if (val === null) {
                val = lists[i].val
            }
            // console.log(lists[i].val, val)
            if (lists[i].val <= val) {
                val = lists[i].val
                j = i
            }
        }
    }
    console.log(j)
    let m = new ListNode(lists[j].val)
    lists[j] = lists[j].next
    
    return m
}

var mergeKLists = function(lists) {
    if (lists.length === 0) return ''
    let result = null
    while (!isOver(lists)) {
        if (!result) {
            result = minNode(lists)
        } else {
            let z = result
            while (z.next) {
              z = z.next
            }
            z.next = minNode(lists)
        }
    }
    
    return result
    
};

In the most extreme case, we need to traverse k linked lists every time we get elements, so the complexity is O (KN), the higher the complexity of k value. Not necessarily faster than method

3. points therapy

We only need to merge the adjacent lists, so that we can merge the lists into a sequential list with only log n operations

The total depth of recursion is logk. The number of recursion operations in each layer is n, and N is the number of all elements. So the total complexity is
O(nlogk)

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    if(lists.length == 0) return null;
    var k = lists.length;
    while(k > 1){
        for (let i = 0; i < ~~(k / 2); i++) {
            lists[i] = mergeTwoLists(lists[i], lists[i + ~~((k + 1) / 2)]);
        }
        k = ~~((k + 1) / 2);
    }
    return lists[0];
};
var mergeTwoLists = function (l1, l2) {
    if (l1 == null) return l2
    if (l2 == null) return l1
    if (l1.val <= l2.val) {
        l1.next = mergeTwoLists(l1.next, l2)
        return l1
    } else {
        l2.next = mergeTwoLists(l1, l2.next)
        return l2
    }
}

Submission