9. Analysis overview of linked list related topics
Link to mind map
Algorithm and data structure mind map
Refer to the course notes of Zuo Cheng cloud system algorithm
Refer to Moke network algorithm system course notes
Summary of common questions:
1. Find the middle node of the linked list
Meaning:
It is designed to find the specified node of the linked list and realize the following four functions:
- 1. Find the middle node of the linked list. If it is an even number, find the floor, that is, round down, which is less than the number of the middle boundary
- 2. Find the middle node of the linked list. If it is an even number, find ceil, that is, round up, which is greater than the number of the middle boundary
- 3. Find the previous node of the intermediate node of the linked list. If it is an even number, find the floor, that is, round down, which is less than the number of intermediate nodes
- 4. Find the previous node of the intermediate node of the linked list. If it is an even number, find ceil, that is, round up, which is greater than the number of intermediate nodes
Solution:
- Use the fast and slow pointer. The number of steps of the fast pointer is twice that of the slow pointer. After the fast pointer is finished, the slow pointer falls on the middle attachment
- For the determination of intermediate node floor, ceil and pre,
- Just adjust the starting position of the fast and slow pointer, and the slow pointer determines whether it is floor or ceil,
- The relative position of the fast and slow pointer determines whether the slow pointer is in the previous position or the middle position
- Pay attention to boundary conditions, avoid null pointer errors, and deal with special cases with less than three nodes
Code implementation:
1. Find the floor of the middle value, that is, round down
-
Define the fast and slow pointer. The slow pointer starts from the starting position, which is rounded down
To fall in the middle position, the fast and slow positions should be consistent with the starting position -
// 1. Find the floor of the middle value, that is, round down public static Node floorMid(Node head) { // Deal with the situation that the number of nodes is less than 3 first if (head == null || head.next == null || head.next.next == null) { return head; } // Define the fast and slow pointer. The slow pointer starts from the starting position, which is rounded down // To fall in the middle position, the fast and slow positions should be consistent with the starting position Node slow = head; Node fast = head; while (fast.next != null && fast.next.next != null) { slow = slow.next; fast = fast.next.next; } return slow; }
2. Find the ceil of the middle value, that is, round up
-
Define the fast and slow pointer. The slow pointer takes one step first, so that the upward rounding of the intermediate value can be found
-
To fall in the middle position, the fast and slow positions should be consistent with the starting position
-
// 2. Find the ceil of the middle value, that is, round up public static Node ceilMid(Node head) { // Deal with the situation that the number of nodes is less than 3 first if (head == null || head.next == null || head.next.next == null) { return head; } // Define the fast and slow pointer. The slow pointer takes one step first, so that the upward rounding of the intermediate value can be found // To fall in the middle position, the fast and slow positions should be consistent with the starting position Node slow = head.next; Node fast = head.next; while (fast.next != null && fast.next.next != null) { slow = slow.next; fast = fast.next.next; } return slow; }
3. Find the previous node of the intermediate value floor, that is, round down
-
Define the fast and slow pointer. The fast pointer takes two more steps first, so that the slow pointer will be one step slower than the middle value
-
That is, the starting position of the fast and slow pointer is relatively two steps away, which is equivalent to that the slow pointer takes one step less to reach the position before the middle value
-
For the floor with intermediate value, the slow pointer can start from the starting position
-
// 3. Find the previous node of the intermediate value floor, that is, round down public static Node preFloorMid(Node head) { // First deal with the case where the number of nodes is < = 2 if (head == null || head.next == null || head.next.next == null) { return null; } // Define the fast and slow pointer. The fast pointer takes two more steps first, so that the slow pointer will be one step slower than the middle value // That is, the starting position of the fast and slow pointer is relatively different by two steps, which is equivalent to one step of the slow pointer Node slow = head; Node fast = slow.next.next; while (fast.next != null && fast.next.next != null) { slow = slow.next; fast = fast.next.next; } return slow; }
4. Find the previous node of the middle value ceil, that is, round up
-
Define the fast and slow pointer. The fast pointer takes two more steps first, so that the slow pointer will be one step slower than the middle value
-
To round up, like ceilMid, the slow pointer first takes a step relative to the starting position
-
The relative position between the fast pointer and the slow pointer is two steps away, which is a complete one-step slow pointer
-
// 4. Find the previous node of the middle value ceil, that is, round up public static Node preCeilMid(Node head) { // First deal with the case where the number of nodes is < = 2 if (head == null || head.next == null || head.next.next == null) { return null; } // Define the fast and slow pointer. The fast pointer takes two more steps first, so that the slow pointer will be one step slower than the middle value // In order to round up, the slow pointer needs to be further. In order to ensure that the slow pointer is one step before the middle value, // The relative position between the fast pointer and the slow pointer is two steps away, which is a complete one-step slow pointer Node slow = head.next; Node fast = slow.next.next; while (fast.next != null && fast.next.next != null) { slow = slow.next; fast = fast.next.next; } return slow; }
Code test:
0->1->2->3->4->5->6->7
floorMid 3 3 ceilMid 4 4 floorPreMid 2 2 ceilPreMid 3 3
0->1->2->3->4->5->6->7->8
floorMid 4 4 ceilMid 4 4 floorPreMid 3 3 ceilPreMid 3 3
Complexity analysis:
- The traversal time of the linked list is O(n)
- All are processed in situ, and the spatial complexity is O(1)
2. Palindrome linked list
Title Link
Meaning:
Given the head node * * of a linked list, please judge whether it is a palindrome linked list.
If a linked list is a palindrome, the sequence of nodes in the linked list is the same from front to back and from back to front.
For example:

input: head = [1,2,3,3,2,1] output: true
Solution:
Solution 1: container stack using additional space O(n)
- Due to the symmetrical structure of palindrome linked list and the characteristics of last in first out of the stack, the elements are in reverse order after leaving the stack
- Judge whether the inverted structure is equal to the original structure to judge whether it is a palindrome linked list
Solution 2: fast and slow pointer, change the linked list structure to facilitate comparison, space O(1)
- 1. First use the fast and slow pointer method to find the position of the intermediate node
- 2. Reverse all nodes in the middle node to the right and change it to point from right to left
- 3. Traverse and compare from both ends of the linked list to the middle in turn. If the nodes are different, end the cycle and draw a judgment
- 4. Note that it is the end of the cycle, not the direct return result, because the original linked list should be restored before ending the program
Code implementation:
Solution 1: stack
// Solution 1: use the stack container, and the palindrome linked list is put on the stack and out of the stack in the same order
public boolean isPalindrome(ListNode head) {
Stack<ListNode> stack = new Stack<>();
// 1. Traverse the linked list in turn and put the nodes on the stack
ListNode cur = head;
while(cur != null) {
stack.push(cur);
cur = cur.next;
}
// 2. Pop the nodes out of the stack in turn and compare them with the original linked list structure for verification
cur = head;
while(!stack.isEmpty()) {
if(cur.val != stack.pop().val) return false;
cur = cur.next;
}
return true;
}
Solution 2: use the fast and slow pointer to change the linked list structure
// Solution 2: fast and slow pointer, change the linked list structure to facilitate comparison, space O(1)
public boolean isPalindrome2(ListNode head) {
if(head == null || head.next == null) return true;
// - 1. First, use the fast and slow pointer method to find the position of the intermediate node
ListNode mid = head;
ListNode right = head;
while(right.next !=null && right.next.next != null) {
mid = mid.next; // The mid finally points to the intermediate node
right = right.next.next;
}
// - 2. Invert all nodes in the middle node to the right and change it to point from right to left
// mid->cur->right ==> null<-mid<-cur<-right
ListNode cur = mid.next; // First node on the right
mid.next = null; // Change the linked list structure so that the intermediate node points to null
while(cur != null) { // Reverse the linked list structure of the intermediate node to the right
right = cur.next;
cur.next = mid;
mid = cur; // The final mid points to the last node in the linked list
cur = right;
}
// - 3. Traverse and compare from both ends of the linked list to the middle in turn. If the nodes are different, end the cycle and draw a judgment
cur = mid; // Record the position of the last node and restore the linked list for the last step
boolean res = true;
while(head != null && mid != null) {
if(head.val != mid.val) {
res = false;
break;
}
head = head.next;
mid = mid.next;
}
// - 4. Note that it is the end of the loop, not the direct return result, because the original linked list should be restored before ending the program
// left<-mid<-cur ==> left->mid->cur->null
mid = cur.next;
cur.next = null;
while(mid != null) {
ListNode left = mid.next;
mid.next = cur;
cur = mid;
mid = left;
}
return res;
}
Complexity analysis:
- Time complexity is O(n)
- With stack, additional space complexity O(n), with fast and slow pointer, space O(1)
3. Separate and rearrange the linked list
Meaning:
- A linked list is divided into three parts: less than V, equal to V and greater than v
- Then reassemble the linked list into a new linked list in the order of less than V, equal to V and greater than v
Solution:
Solution 1: using array container method
- 1. Count the number of nodes in the linked list and create an array container of the corresponding size
- 2. Traverse again and add the linked list node to the array container
- 3. Divide the array into three regions
- 4. String the ordered array elements into a linked list, that is, the final required linked list structure
Solution 2: use the pointer to sort the linked list in place
- 1. Use six pointers to point to the head and tail nodes of the three regions respectively, and traverse the linked list once to divide the linked list
- 2. Judge and verify each node, compare with the size of v, and put it into the specified interval,
- To break the next node of the current node, create a new node and save the next node to be processed
- 3. Finally, splice the three linked lists
- The tail connection between cells is equal to the head of the interval, and the tail connection of the interval is greater than the head of the interval
- Pay attention to the boundary conditions, i.e. whether the interval is less than or equal to the interval is empty or not, which needs special treatment
Code implementation:
Solution 1: use array fast sorting
// Solution 1: use the container to load the linked list nodes into the array, sort them, and then string them into a linked list
public static Node listPartition1(Node head, int pivot) {
if(head == null) return null;
// - 1. Count the number of nodes in the linked list and create an array container of the corresponding size
int size = 0;
Node cur = head;
while(cur != null) {
size ++;
cur = cur.next;
}
Node[] arr = new Node[size];
// - 2. Traverse again and add the linked list node to the array container
int i = 0;
cur = head;
for(i = 0; i < arr.length; i ++) {
arr[i] = cur;
cur = cur.next;
}
// - 3. Carry out a fast three-way sorting method for array elements and divide them into three areas (one line at a time, each area does not need to be sorted)
partition(arr, pivot);
// - 4. String the ordered array elements into a linked list, that is, the final required linked list structure
for(i = 1; i < arr.length; i ++) {
arr[i - 1].next = arr[i];
}
arr[i - 1].next = null;
return arr[0];
}
private static void partition(Node[] arr, int pivot) {
// 1. First define the pointer and divide it into three intervals
// [0, pL]<v, [pL + 1, pR - 1]=v,[pR,n - 1]>v
int pL = -1; // pL points to a number less than v
int i = 0; // i points to a number equal to v
int pR = arr.length; // pR points to a number greater than v
// 2.i traverse in turn and put the elements in the specified interval
while(i < pR) {
if(arr[i].value < pivot) {
swap(arr, i ++, ++pL); // First open up space, move the pointer to the correct position, and then put the value
} else if(arr[i].value > pivot) {
swap(arr, i, --pR); // Continue to judge and verify the number exchanged from the right
} else {
i ++;
}
}
}
private static void swap(Node[] arr, int i, int j) {
Node t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
Solution 2: use the multi pointer method to segment the linked list in situ
// Solution 2: use multiple pointers to determine three intervals for segmentation and then splicing
public static Node listPartition2(Node head, int pivot) {
if(head == null) return null;
// - 1. Use 6 pointers to point to the head and tail nodes of the three regions respectively, and traverse the linked list once to divide the linked list
Node sH = null; // small head
Node sT = null; // small tail
Node eH = null; // equal head
Node eT = null; // equal tail
Node mH = null; // big head
Node mT = null; // big tail
// - 2. Judge and verify each node, compare with the size of v, and put it into the specified interval,
// -To break the next node of the current node, create a new node and save the next node to be processed
Node cur = head; // Nodes to process
Node next = null; // Save the next node to process
while(cur != null) {
next = cur.next;
cur.next = null; // The node next to be processed should be disconnected to avoid a node being pointed to by the next of multiple nodes
if(cur.value < pivot) {
if(sH == null) {
sH = cur;
sT = cur;
} else {
sT.next = cur;
sT = cur;
}
} else if(cur.value == pivot) {
if(eH == null) {
eH = cur;
eT = cur;
} else {
eT.next = cur;
eT = cur;
}
} else {
if(mH == null) {
mH = cur;
mT = cur;
} else {
mT.next = cur;
mT = cur;
}
}
cur = next;
}
// - 3. Finally, the three linked lists are spliced
// -The tail connection between cells is equal to the head of the interval, and the tail connection of the interval is greater than the head of the interval
// -Pay attention to the boundary conditions, i.e. equal to the interval and greater than whether the interval is empty. Special treatment shall be made
// First deal with the case that the area less than or equal to the area is not completely null. You need to connect the areas
if(sT != null) { // Indicates that there is an area less than, but not necessarily equal to
sT.next = eH;
// Judge whether there is an equal area and check whether eT is empty
eT = eT == null ? sT : eT; // Next, whoever connects the head larger than the area will become eT
}
if(eT != null) { // Exclusion means that there is neither less than the area nor equal to the area
eT.next = mH; // No matter whether there is a larger area or not, the linked list is complete
}
// If the area less than or equal to the area is null, you can directly find the node greater than the area head
return sH != null ? sH : (eH != null ? eH : mH);
}
Complexity analysis:
- The time complexity is O(n)
- Using array, extra space O(n), using multi pointer method, extra space O(1)
4. Split linked list expansion problem
Split linked list to expand topic links
Meaning:
-
Give you a head node of the linked list and a specific value x. please separate the linked list,
- Make all nodes less than x appear before nodes greater than or equal to X.
-
You should keep the initial relative position of each node in both partitions.
For example:
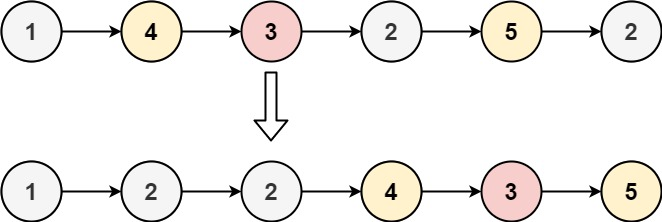
Input: head = [1,4,3,2,5,2], x = 3 Output:[1,2,2,4,3,5]
Solution:
- To ensure that the initial relative position of each node remains unchanged, it is difficult to meet the requirements for fast scheduling with containers
- Therefore, we must use multiple pointers to split the linked list in place, which is similar to the above question,
- First divide the interval to be divided, then put the node into the specified interval, and finally connect the two intervals
code implementation
public ListNode partition(ListNode head, int x) {
if(head == null) return null;
// 1. Define the pointer and divide it into two intervals
ListNode smallHead = null;
ListNode smallTail = null;
ListNode rightHead = null;
ListNode rigthTail = null;
// 2. Divide the linked list nodes into two sections as required
ListNode cur = head;
ListNode next = null;
while(cur != null) {
next = cur.next;
cur.next = null;
if(cur.val < x) {
if(smallHead == null) {
smallHead = cur;
smallTail = cur;
} else {
smallTail.next = cur;
smallTail = cur;
}
} else {
if(rightHead == null) {
rightHead = cur;
rigthTail = cur;
} else {
rigthTail.next = cur;
rigthTail = cur;
}
}
cur = next;
}
// 3. Splice the linked lists of the two sections
if(smallTail != null) {
smallTail.next = rightHead;
}
return smallHead != null ? smallHead : rightHead;
}
Complexity:
- Time O(n), space O(1)
5. Copy the linked list with random pointer
Title Link
Meaning:
- Implement the copyRandomList function to copy a complex linked list.
- In a complex linked list, each node has a next pointer to the next node,
- There is also a random pointer to any node in the linked list or null.
For example:
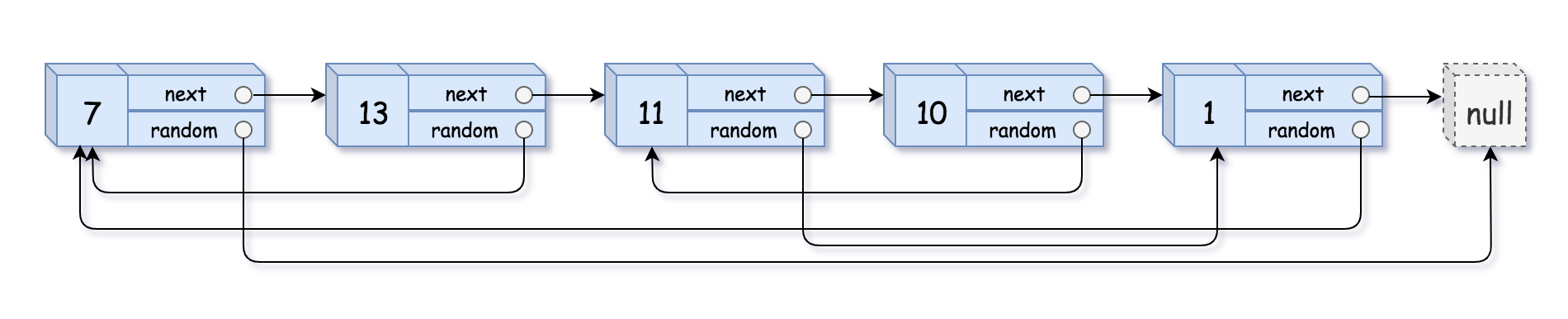
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]] Output:[[7,null],[13,0],[11,4],[10,2],[1,0]]
Solution:
Solution 1: use container, map
- 1. Using map container and map mapping is shadow engineering
- 2. Add a key value pair. The old node maps to the new node. Key is the old node and value is the new node
- 3. Add the next of the new linked list node. Random, refer to the next and random of the node corresponding to the old linked list
Solution 2: do not use containers and dispose in situ
- 1. To save space, create a new shadow node behind each node, which is similar to map mapping
- 2. Use the mapping of the old node to handle the random pointer of the new node
- 3. Finally, disconnect the old and new nodes and separate the new and old linked lists in the next direction
Code implementation:
Solution 1: use container, map
// Solution 1: map with map container
public Node copyRandomList(Node head) {
if(head == null) return null;
// - 1. Using map container and map mapping is shadow engineering
Map<Node, Node> map = new HashMap<>();
// - 2. Add a key value pair. The old node maps to the new node. Key is the old node and value is the new node
Node cur = head;
while(cur != null) {
map.put(cur, new Node(cur.val));
cur = cur.next;
}
// - 3. Add the next of the new linked list node. Random, refer to the next and random of the node corresponding to the old linked list
cur = head;
while(cur != null) {
map.get(cur).next = map.get(cur.next);
map.get(cur).random = map.get(cur.random);
cur = cur.next;
}
return map.get(head);
}
Solution 2: use another pointer to maintain a new linked list
// Solution 2: use the pointer to deal with the linked list in situ
public Node copyRandomList(Node head) {
if(head == null) return null;
// - 1. Create a shadow team first
// To save space, create a new shadow node behind each node, which is similar to map mapping
Node pit1 = head;
Node pit2 = null; // Shadow node
// 1 -> 2 -> 3 -> null
// 1 -> 1' -> 2 -> 2' -> 3 -> 3'
while(pit1 != null) {
pit2 = new Node(pit1.val); // New node
pit2.next = pit1.next; // Add the new node to the linked list
pit1.next = pit2;
pit1 = pit1.next.next;
}
// - 2. The random pointer of forming a shadow team
// Use the mapping of the old node to handle the random pointer of the new node
pit1 = head;
while(pit1 != null) {
pit2 = pit1.next;
// Pay attention to whether the random of the old linked list is null, otherwise random Next null pointer exception
pit2.random = pit1.random != null ? pit1.random.next : null;
pit1 = pit1.next.next; // Continue to find the next old node
}
// - 3. Break away from the original team and lead the team by yourself
// Finally, disconnect the old and new nodes and handle the next pointer
pit1 = head;
Node res = pit1.next; // Keep the head node of the new linked list as the returned result
while(pit1 != null) {
pit2 = pit1.next;
pit1.next = pit1.next.next; // Change the next pointer of the old node
// Change the next pointer of the new node to point to the next shadow node
// Similarly, to handle the case where the new node is the last node, the null pointer exception
pit2.next = pit2.next != null ? pit2.next.next : null;
pit1 = pit1.next;
}
return res;
}
Complexity analysis:
- Time complexity is O(n)
- Use container, space O(n), do not use container O(1)