leetcode official website: https://leetcode-cn.com/problems
CS-Notes: https://www.cyc2018.xyz/

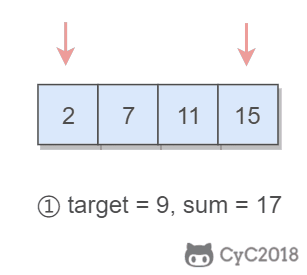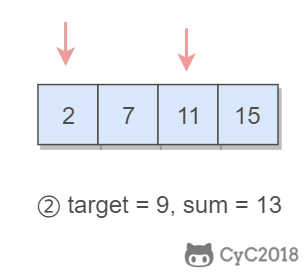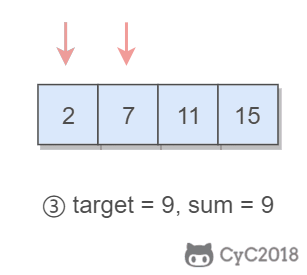
1. Sum of two II - input ordered array (7 / 21-167)

Problem solving ideas:

Using double pointers, one pointer points to an element with a smaller value and one pointer points to an element with a larger value. Pointers to smaller elements traverse from head to tail, and pointers to larger elements traverse from tail to head.

If two pointers point to the sum of elements sum == target，Then get the required results;
If sum > target，Move larger elements so that sum Smaller;
If sum < target，Move smaller elements so that sum Get bigger.

The elements in the array can be traversed at most once, and the time complexity is O(N). Only two additional variables are used, and the spatial complexity is O(1).

java code implementation:

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        if(numbers == null) return null;
        int i = 0, j = numbers.length - 1;
        while(i<j) {
            int sum = numbers[i] + numbers[j];
            if(sum == target) {
                return new int[]{i+1,j+1};
            }else if(sum < target){
                i++;
            }else{
                j--;
            }
        }
        return null;
    }
}

2. Sum of squares (7 / 21-633)

Resolution:

It can be regarded as finding two numbers in an ordered array with elements 0~target, so that the sum of squares of the two numbers is target. If it can be found, it returns true, indicating that target is the sum of squares of two integers.

This question and 167 Two sum II - input array is sorted is similar, with only one obvious difference: one is and is target, and the other is the sum of squares is target. You can also use double pointers to get two numbers so that the sum of squares is target.

The key of this problem is the initialization of the right pointer to realize pruning, so as to reduce the time complexity. Set the right pointer as X and the left pointer as 0. In order to make the value of 02 + x2 as close to the target as possible, we can take x as sqrt(target).

Because you only need to traverse 0~sqrt(target) once at most, the time complexity is O(sqrt(target)). Because only two additional variables are used, the spatial complexity is O(1).

Java implementation:

class Solution {
    public boolean judgeSquareSum(int c) {
        int left = 0, right = (int)Math.sqrt(c);
        while(left <= right) {
            int sum = left*left + right*right;
            if(sum == c) {
                return true;
            }else if(sum < c) {
                ++left;
            }else {
                --right;
            }
        }
        return false;
    }
}

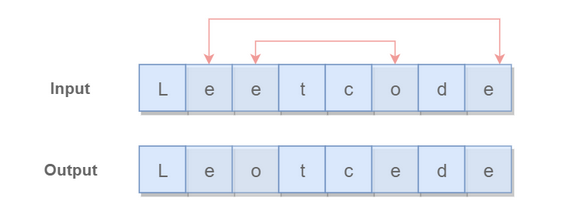
3. Invert vowels in string (7 / 21-345)

Resolution:

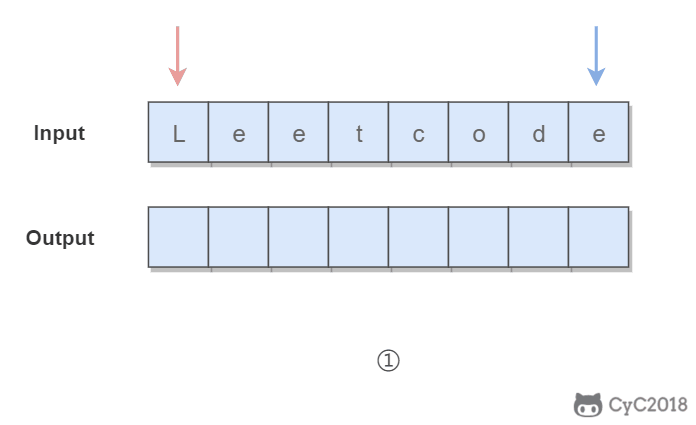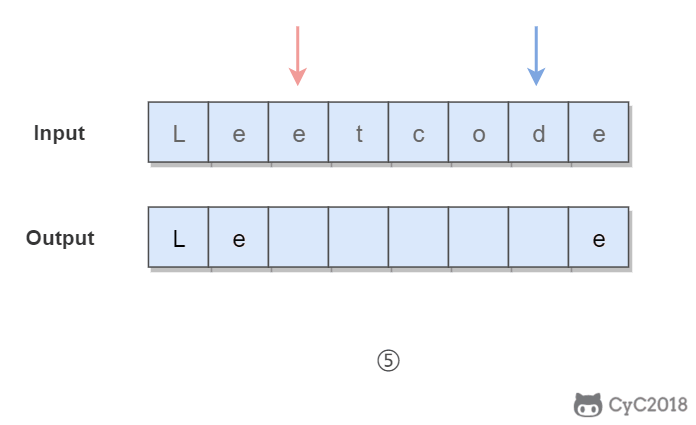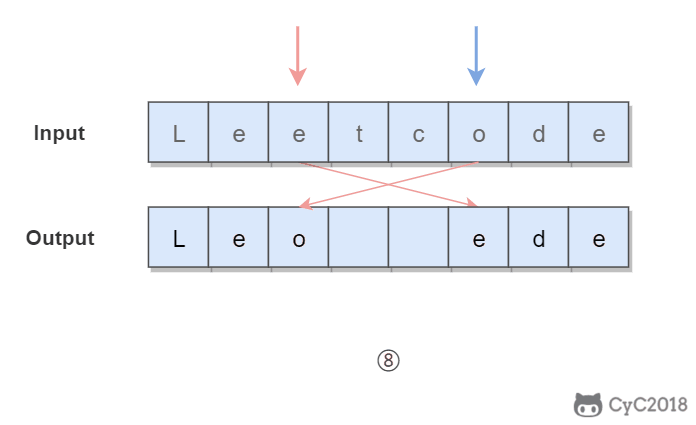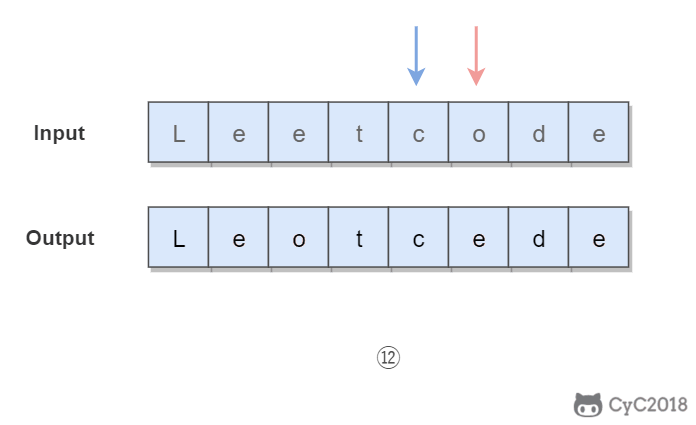
Double pointers are used. One pointer traverses from head to tail and the other traverses from tail to head. When both pointers traverse vowel characters, the two vowel characters are exchanged.

In order to quickly determine whether a character is a vowel character, we add all vowel characters to the set HashSet, so as to perform the operation with the time complexity of O(1).

The time complexity is O(N): You only need to traverse all elements once
 Spatial complexity O(1): You only need to use two additional variables

Java implementation:

class Solution {
    //Vowel set
    private final static HashSet<Character> vowels = new HashSet<>( //Create a HashSet collection object
        Arrays.asList('a','e','i','o','u','A','E','I','O','U')
    );

    public String reverseVowels(String s) {
        if(s == null) return null;
        int left = 0, right = s.length() -1;
        char[] result = new char[s.length()];
        while(left <= right) {
            char cl = s.charAt(left);  // charAt returns the character at position i
            char cr = s.charAt(right);
            if(!vowels.contains(cl)) {
                result[left++] = cl;   //If not, it is stored as a direct array
            } else if(!vowels.contains(cr)) {
                result[right--] = cr;  //If not, it is stored as a direct array
            } else {
                result[left++] = cr;   //When both sides contain, they are exchanged first and then stored in the array
                result[right--] = cl;
            }
        }
        return new String(result); 
    }
}

4. Verify palindrome string II (7 / 21-680)

Resolution:

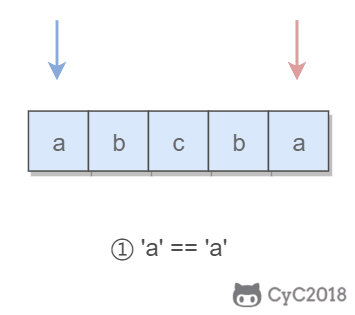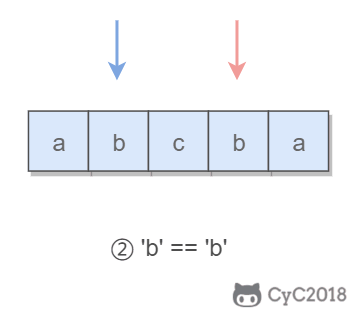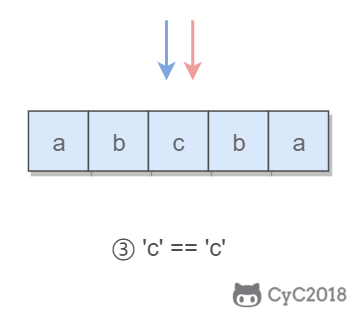
The so-called palindrome string refers to a string with left-right symmetry. For example, "abcba" is a palindrome string.

Using double pointers, it is easy to judge whether a string is a palindrome string: make a pointer traverse from left to right and a pointer traverse from right to left. The two pointers move one position at the same time, and judge whether the characters pointed to by the two pointers are the same each time. If they are the same, the string is a palindrome string with left-right symmetry.

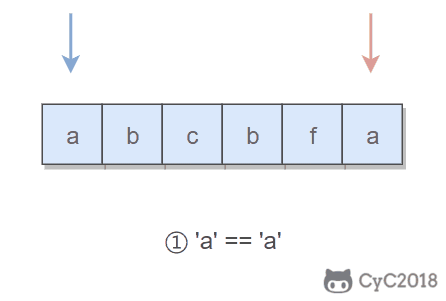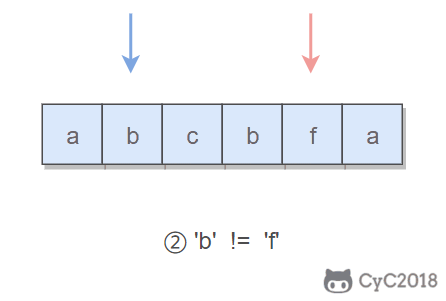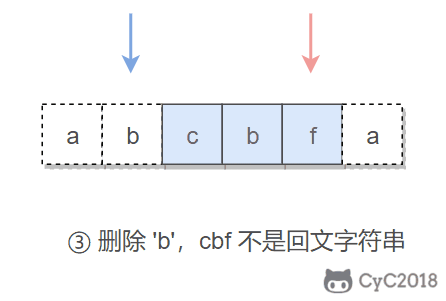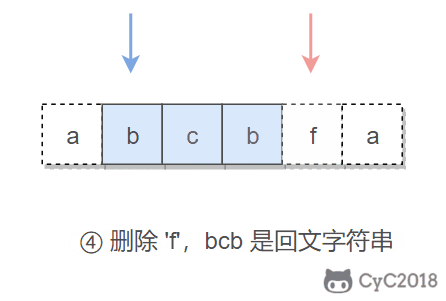
The key to this problem is to delete a character. When traversing a string with double pointers, if the characters pointed to by the two pointers are not equal, we try to delete one character, and then judge whether the deleted string is a palindrome string.

When judging whether it is a palindrome string, we do not need to judge the whole string, because the characters to the left and right of the left pointer have been judged to be symmetrical before, so we only need to judge the middle substring.

When trying to delete characters, we can delete both the characters pointed by the left pointer and the characters pointed by the right pointer.

Java implementation:

class Solution {
    public boolean validPalindrome(String s) {
        for (int i = 0, j = s.length() - 1; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return isPalindrome(s, i, j - 1) || isPalindrome(s, i + 1, j);
            }
        }
        return true;
    }

    private boolean isPalindrome(String s, int i, int j) {
        while (i < j) {
            if (s.charAt(i++) != s.charAt(j--)) {
                return false;
            }
        }
        return true;
    }

}

5. Merge two ordered arrays (7 / 27-88)

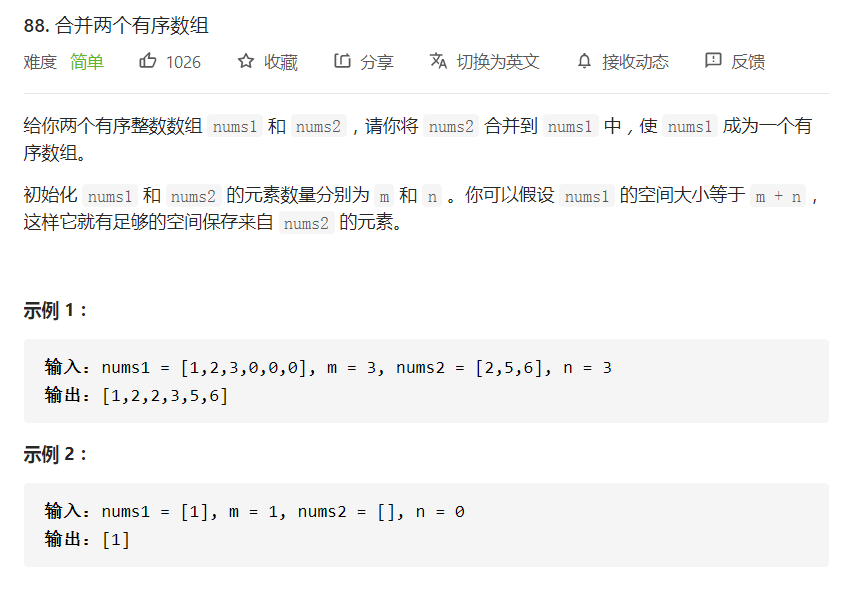
Resolution:

You need to traverse from the tail, otherwise the value obtained by merging on nums1 will overwrite the value that has not been merged and compared.

Java implementation:

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i1 = m-1, i2 = n-1;
        int i3 = m+n-1;
        while(i2 >= 0){
            if(i1 < 0){
                nums1[i3--] = nums2[i2--];
            }else if(i2 < 0){
                nums1[i3--] = nums1[i1--];
            }else if(nums1[i1] > nums2[i2]){
                nums1[i3--] = nums1[i1--];
            }else{
                nums1[i3--] = nums2[i2--];
            }
        } 
    }
}

6. Circular linked list (7 / 27-141)

Resolution:

Using double pointers, one pointer moves one node at a time, and one pointer moves two nodes at a time. If there is a ring, the two pointers must meet.

Java implementation:

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head == null){
            return false;
        }
        ListNode l1 = head, l2 = head.next;
        while(l1 != null && l2 != null && l2.next != null){
            if(l1 == l2){
                return true;
            }
            l1 = l1.next;
            l2 = l2.next.next;
        }
        return false;
    }
}

7. Match the longest word in the dictionary by deleting letters (7 / 27-524)

Resolution:

By deleting a character in the string s, the string t can be obtained. It can be considered that t is a subsequence of S. we can use double pointers to judge whether a string is a subsequence of another string.

Java implementation:

class Solution {
    public String findLongestWord(String s, List<String> dictionary) {
        String longsetWord = "";
        for(String targer : dictionary){
            int l1 = longsetWord.length(), l2 = targer.length();
            if(l1 > l2 || (l1 == l2 && longsetWord.compareTo(targer) < 0)){ //longsetWord. CompareTo (TAR): if the string is less than the string parameter, a value less than 0 will be returned;
                continue;
            }
            if(isSubstr(s,targer)){
                longsetWord = targer;
            }
        }
        return longsetWord;
    }

    //Judge whether two strings are equal
    private boolean isSubstr(String s, String targer) {
        int i = 0, j = 0;
        while(i < s.length() && j < targer.length()) {
            if(s.charAt(i) == targer.charAt(j)) {  // s.charAt(i) means: get the character with subscript i in S
                j++;
            } 
            i++;
        }
        return j == targer.length();
    }
}