Suffix and array
Suffix array actually represents all suffix strings. After ranking, write them down from No. 0 to No. 7 in turn. This is the so-called suffix array
There will not be the same ranking because the length is different

Generate suffix array
1) Violence solving:
Mr. into all suffix strings, complexity O (N^2)
Number of suffix strings O (n), sorting of N suffix strings, cost O (N*logN)
2) DC3 solution: O (N)
Group according to subscript module 3 and do something similar to recursion to quickly solve this problem. There is a premise that at the beginning, each value in the array should not be too large. If it is too large, the constant term will be a little large
DC3 steps
1) First, do small label classification
I% 3 = = 0 = = > class 0 subscript, code s0
i%3==1 ==> Class 1 small label, code s1
i%3==2 ==> Class 2 small label, code s2
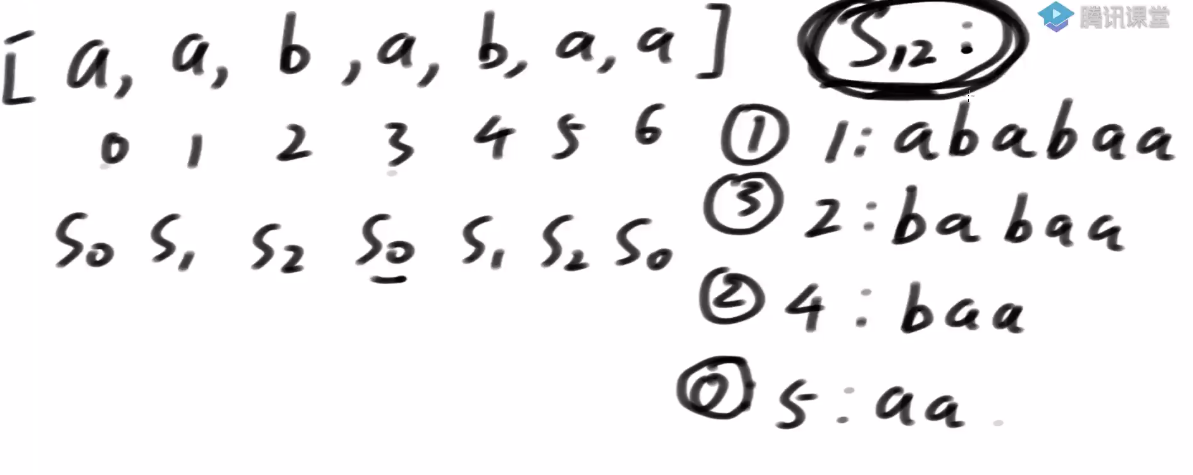
2) Get the rank of s12 suffix string (assuming it can be obtained)
3) When there is s12 ranking, the internal ranking of s0 can be directly determined by a cardinality ranking
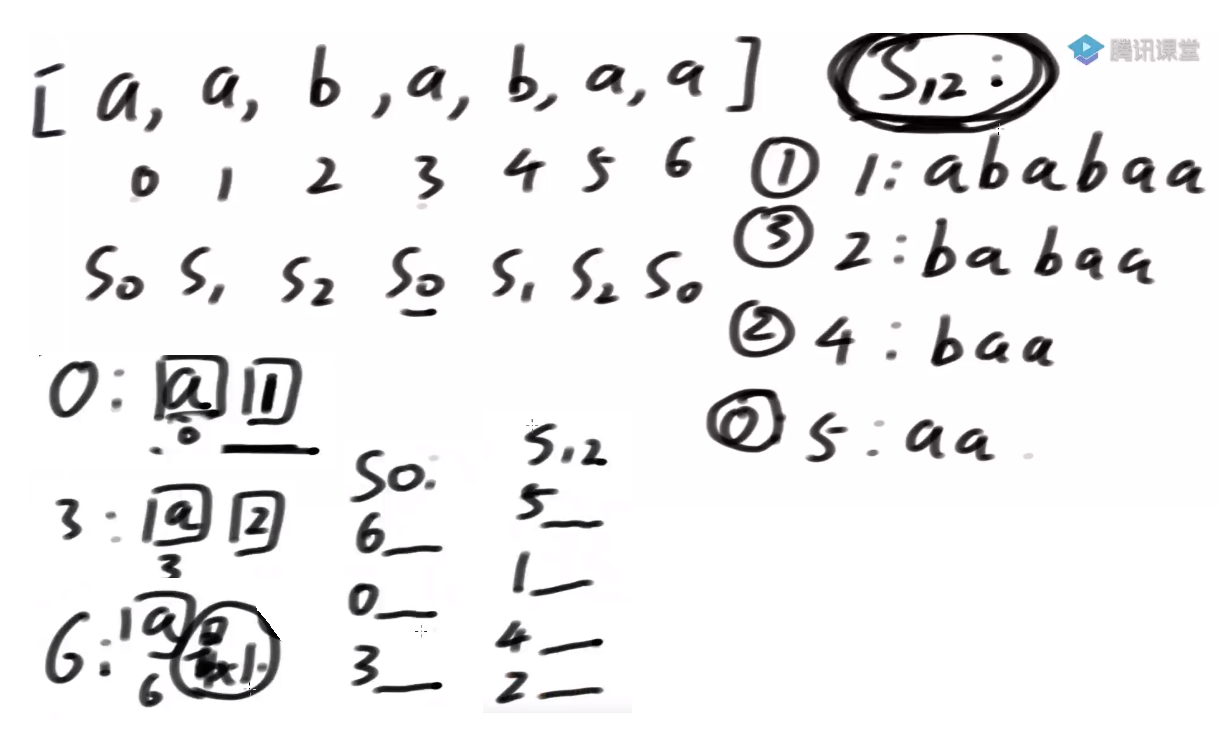
4) After having the s12 sort and s0 sort, use a merge to obtain the overall sort s012,
Compare strings starting with 6 and 5 first
There are at most 3 times between s0 and s2
s0 and s1 classes can be compared at most 2 times
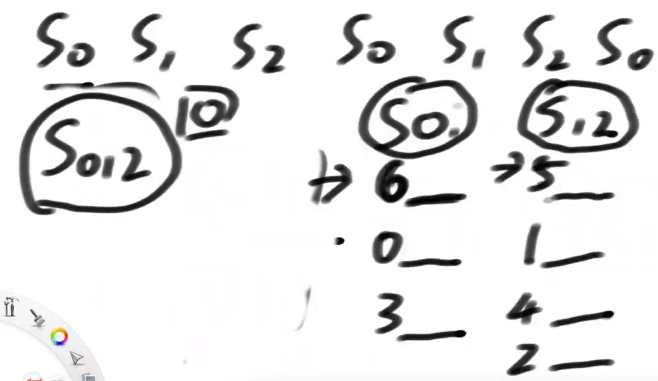


Conclusion: if we have the ranking of s12, we can use O(N) time to get the internal ranking of s0, and we can also use O(N) time merge s012 overall rankings are sorted by cardinality in the later time. There are three types of data at most. Therefore, once the s12 ranking is completed, the algorithm is O(N)
5) How to get the ranking of s12?
1. Can you get an accurate ranking only by taking the first three characters?
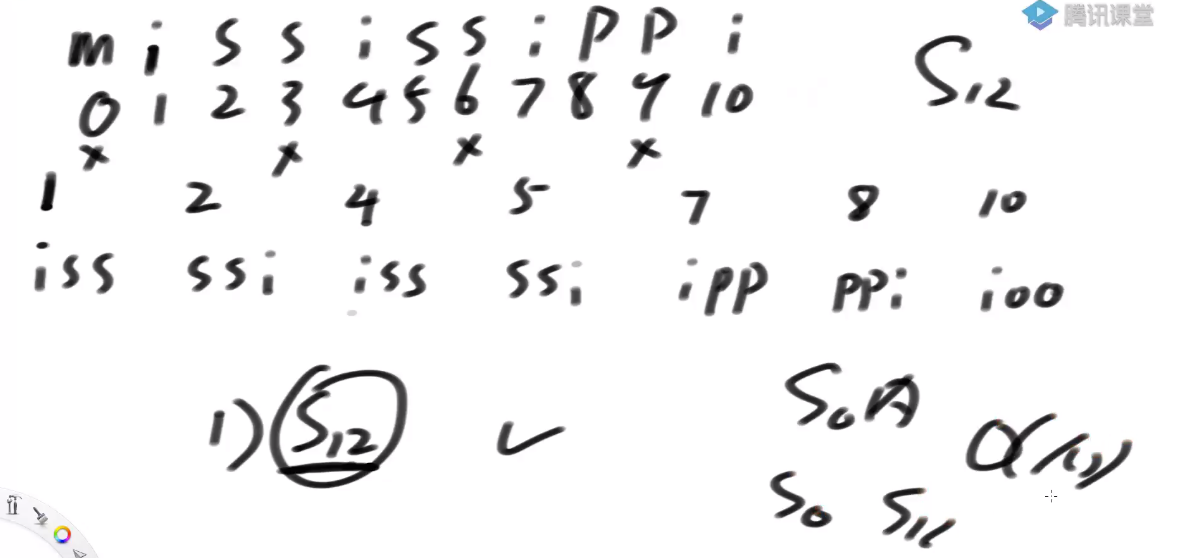
2. If you can't tell the exact ranking

3. Form a new array. s1 class is placed on the left and s2 class is placed on the right. If I lack it, let it be next to it
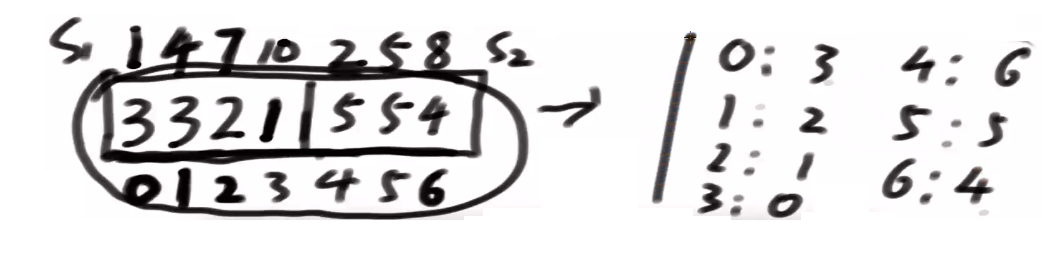

6) Suffix array generated by DC3 algorithm: sa array rank array
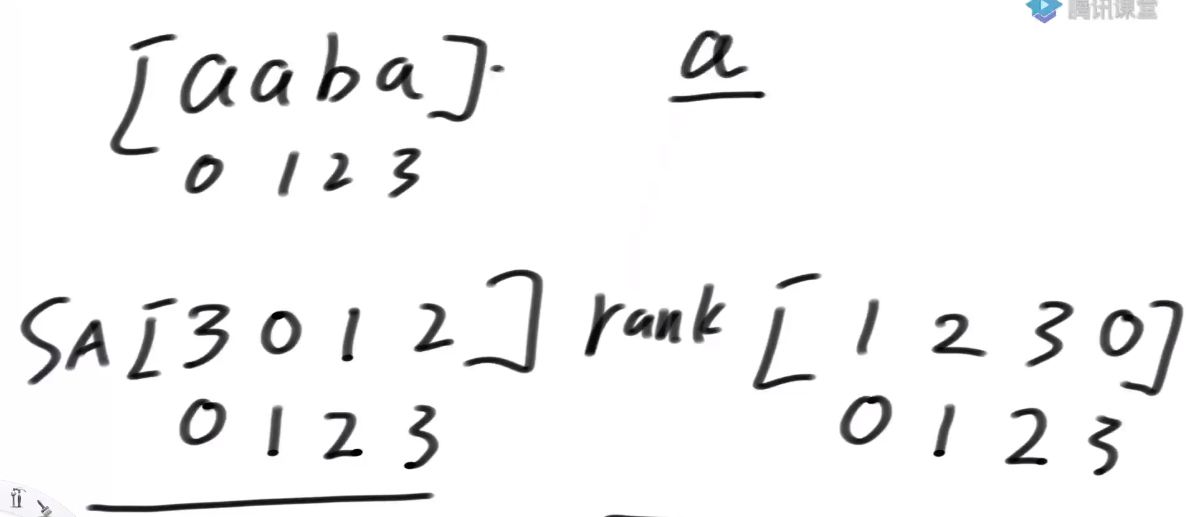
public class DC3 {
public int[] sa;
public int[] rank;
public int[] height;
// Agreement on construction method:
// The array is called nums. If you are a string, please convert it to an integer array nums
// In the array, the minimum value is > = 1
// If it is not satisfied, it will be treated as satisfied and will not affect the use
// What is the maximum value in Max and num
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
height = height(nums);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
private int[] height(int[] s) {
int n = s.length;
int[] ans = new int[n];
for (int i = 0, k = 0; i < n; ++i) {
if (rank[i] != 0) {
if (k > 0) {
--k;
}
int j = sa[rank[i] - 1];
while (i + k < n && j + k < n && s[i + k] == s[j + k]) {
++k;
}
ans[rank[i]] = k;
}
}
return ans;
}
// To test
public static int[] randomArray(int len, int maxValue) {
int[] arr = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = (int) (Math.random() * maxValue) + 1;
}
return arr;
}
// To test
public static void main(String[] args) {
int len = 100000;
int maxValue = 100;
long start = System.currentTimeMillis();
new DC3(randomArray(len, maxValue), maxValue);
long end = System.currentTimeMillis();
System.out.println("Data volume " + len + ", Running time " + (end - start) + " ms");
}
}Topic 1
https://leetcode.com/problems/last-substring-in-lexicographical-order/
Give you a string s. Find all its substrings and arrange them in dictionary order, and return the last substring.
Using sa array of DC3 to solve
public static String lastSubstring(String s) {
if (s == null || s.length() == 0) {
return s;
}
int N = s.length();
char[] str = s.toCharArray();
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (char cha : str) {
min = Math.min(min, cha);
max = Math.max(max, cha);
}
int[] arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = str[i] - min + 1;
}
DC3 dc3 = new DC3(arr, max - min + 1);
return s.substring(dc3.sa[N - 1]);
}
public static class DC3 {
public int[] sa;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
}Topic 2
Given two strings str1 and str2,
Want to insert str2 as a whole into a position in str1
Form the largest dictionary order
Returns the result with the largest dictionary order
// Violent methods
public static String right(String s1, String s2) {
if (s1 == null || s1.length() == 0) {
return s2;
}
if (s2 == null || s2.length() == 0) {
return s1;
}
String p1 = s1 + s2;
String p2 = s2 + s1;
String ans = p1.compareTo(p2) > 0 ? p1 : p2;
for (int end = 1; end < s1.length(); end++) {
String cur = s1.substring(0, end) + s2 + s1.substring(end);
if (cur.compareTo(ans) > 0) {
ans = cur;
}
}
return ans;
}// rank array of formal method O(N+M) + O(M^2) DC3
// N: S1 length
// M: S2 length
public static String maxCombine(String s1, String s2) {
if (s1 == null || s1.length() == 0) {
return s2;
}
if (s2 == null || s2.length() == 0) {
return s1;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int N = str1.length;
int M = str2.length;
int min = str1[0];
int max = str1[0];
for (int i = 1; i < N; i++) {
min = Math.min(min, str1[i]);
max = Math.max(max, str1[i]);
}
for (int i = 0; i < M; i++) {
min = Math.min(min, str2[i]);
max = Math.max(max, str2[i]);
}
int[] all = new int[N + M + 1];
int index = 0;
for (int i = 0; i < N; i++) {
all[index++] = str1[i] - min + 2;
}
all[index++] = 1;
for (int i = 0; i < M; i++) {
all[index++] = str2[i] - min + 2;
}
DC3 dc3 = new DC3(all, max - min + 2);
int[] rank = dc3.rank;
int comp = N + 1;
for (int i = 0; i < N; i++) {
if (rank[i] < rank[comp]) {
int best = bestSplit(s1, s2, i);
return s1.substring(0, best) + s2 + s1.substring(best);
}
}
return s1 + s2;
}
public static int bestSplit(String s1, String s2, int first) {
int N = s1.length();
int M = s2.length();
int end = N;
for (int i = first, j = 0; i < N && j < M; i++, j++) {
if (s1.charAt(i) < s2.charAt(j)) {
end = i;
break;
}
}
String bestPrefix = s2;
int bestSplit = first;
for (int i = first + 1, j = M - 1; i <= end; i++, j--) {
String curPrefix = s1.substring(first, i) + s2.substring(0, j);
if (curPrefix.compareTo(bestPrefix) >= 0) {
bestPrefix = curPrefix;
bestSplit = i;
}
}
return bestSplit;
}
public static class DC3 {
public int[] sa;
public int[] rank;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
}
Topic 3
https://leetcode.com/problems/create-maximum-number/
Give two integer arrays nums1 and nums2 with lengths M and N respectively, where each value is not greater than 9, and then give a positive number K. You can choose numbers from nums1 and nums2. You are required to choose a total of K numbers from left to right. Returns the result representing the largest number of all possible results.
public static int[] maxNumber1(int[] nums1, int[] nums2, int k) {
int len1 = nums1.length;
int len2 = nums2.length;
if (k < 0 || k > len1 + len2) {
return null;
}
int[] res = new int[k];
int[][] dp1 = getdp(nums1); // Generate the table dp1. In the future, just fix N numbers from nums1,
int[][] dp2 = getdp(nums2);
// get1 gets the quantity from arr1
// K - the quantity taken by GET1 from arr2
for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {
// How to get an optimal result when arr1 selects get1
int[] pick1 = maxPick(nums1, dp1, get1);
int[] pick2 = maxPick(nums2, dp2, k - get1);
int[] merge = merge(pick1, pick2);
res = preMoreThanLast(res, 0, merge, 0) ? res : merge;
}
return res;
}
public static int[] merge(int[] nums1, int[] nums2) {
int k = nums1.length + nums2.length;
int[] ans = new int[k];
for (int i = 0, j = 0, r = 0; r < k; ++r) {
ans[r] = preMoreThanLast(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];
}
return ans;
}
public static boolean preMoreThanLast(int[] nums1, int i, int[] nums2, int j) {
while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {
i++;
j++;
}
return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);
}
public static int[][] getdp(int[] arr) {
int size = arr.length; // 0~N-1
int pick = arr.length + 1; // 1 ~ N
int[][] dp = new int[size][pick];
// Get doesn't start with 0 because it's meaningless to get 0
for (int get = 1; get < pick; get++) { // 1 ~ N
int maxIndex = size - get;
// i~N-1
for (int i = size - get; i >= 0; i--) {
if (arr[i] >= arr[maxIndex]) {
maxIndex = i;
}
dp[i][get] = maxIndex;
}
}
return dp;
}
public static int[] maxPick(int[] arr, int[][] dp, int pick) {
int[] res = new int[pick];
for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {
res[resIndex] = arr[dp[dpRow][pick]];
dpRow = dp[dpRow][pick] + 1;
}
return res;
}public static int[] maxNumber2(int[] nums1, int[] nums2, int k) {
int len1 = nums1.length;
int len2 = nums2.length;
if (k < 0 || k > len1 + len2) {
return null;
}
int[] res = new int[k];
int[][] dp1 = getdp(nums1);
int[][] dp2 = getdp(nums2);
for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {
int[] pick1 = maxPick(nums1, dp1, get1);
int[] pick2 = maxPick(nums2, dp2, k - get1);
int[] merge = mergeBySuffixArray(pick1, pick2);
res = moreThan(res, merge) ? res : merge;
}
return res;
}
public static boolean moreThan(int[] pre, int[] last) {
int i = 0;
int j = 0;
while (i < pre.length && j < last.length && pre[i] == last[j]) {
i++;
j++;
}
return j == last.length || (i < pre.length && pre[i] > last[j]);
}
public static int[] mergeBySuffixArray(int[] nums1, int[] nums2) {
int size1 = nums1.length;
int size2 = nums2.length;
int[] nums = new int[size1 + 1 + size2];
for (int i = 0; i < size1; i++) {
nums[i] = nums1[i] + 2;
}
nums[size1] = 1;
for (int j = 0; j < size2; j++) {
nums[j + size1 + 1] = nums2[j] + 2;
}
DC3 dc3 = new DC3(nums, 11);
int[] rank = dc3.rank;
int[] ans = new int[size1 + size2];
int i = 0;
int j = 0;
int r = 0;
while (i < size1 && j < size2) {
ans[r++] = rank[i] > rank[j + size1 + 1] ? nums1[i++] : nums2[j++];
}
while (i < size1) {
ans[r++] = nums1[i++];
}
while (j < size2) {
ans[r++] = nums2[j++];
}
return ans;
}
public static class DC3 {
public int[] sa;
public int[] rank;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
}
public static int[][] getdp(int[] arr) {
int size = arr.length; // 0~N-1
int pick = arr.length + 1; // 1 ~ N
int[][] dp = new int[size][pick];
// Get doesn't start with 0 because it's meaningless to get 0
for (int get = 1; get < pick; get++) { // 1 ~ N
int maxIndex = size - get;
// i~N-1
for (int i = size - get; i >= 0; i--) {
if (arr[i] >= arr[maxIndex]) {
maxIndex = i;
}
dp[i][get] = maxIndex;
}
}
return dp;
}
public static int[] maxPick(int[] arr, int[][] dp, int pick) {
int[] res = new int[pick];
for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {
res[resIndex] = arr[dp[dpRow][pick]];
dpRow = dp[dpRow][pick] + 1;
}
return res;
}Topic 4
The longest common substring problem is one of the common interview questions. Suppose str1 length N and str2 length M
Generally, the solution of O(N*M) is excellent in the interview field
Because we get the solution of O(N*M), we already need to use dynamic programming
But in fact, the optimal solution of this problem is O(N+M), which requires suffix array + height array
Height array: height[i] refers to the longest common prefix of the i-th and i-1 st names in sa
public static int lcs1(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int row = 0;
int col = str2.length - 1;
int max = 0;
while (row < str1.length) {
int i = row;
int j = col;
int len = 0;
while (i < str1.length && j < str2.length) {
if (str1[i] != str2[j]) {
len = 0;
} else {
len++;
}
if (len > max) {
max = len;
}
i++;
j++;
}
if (col > 0) {
col--;
} else {
row++;
}
}
return max;
}// The longest common substring question is one of the common interview questions
// Suppose str1 length N and str2 length M
// Because of the difficulty of the optimal solution, the solution of O(N*M) is generally excellent in the interview field
// Because we get the solution of O(N*M), we already need to use dynamic programming
// But in fact, the optimal solution of this problem is O(N+M). It is not easy to achieve this complexity
// First, we need to use the DC3 algorithm to get the suffix array (sa)
// Then use sa array to generate height array
// Moreover, there is a non fallback optimization during generation, which is very difficult to understand
// This is the position of suffix array in interview algorithm: the nightmare of high prestige
public static int lcs2(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int N = str1.length;
int M = str2.length;
int min = str1[0];
int max = str1[0];
for (int i = 1; i < N; i++) {
min = Math.min(min, str1[i]);
max = Math.max(max, str1[i]);
}
for (int i = 0; i < M; i++) {
min = Math.min(min, str2[i]);
max = Math.max(max, str2[i]);
}
int[] all = new int[N + M + 1];
int index = 0;
for (int i = 0; i < N; i++) {
all[index++] = str1[i] - min + 2;
}
all[index++] = 1;
for (int i = 0; i < M; i++) {
all[index++] = str2[i] - min + 2;
}
DC3 dc3 = new DC3(all, max - min + 2);
int n = all.length;
int[] sa = dc3.sa;
int[] height = dc3.height;
int ans = 0;
for (int i = 1; i < n; i++) {
int Y = sa[i - 1];
int X = sa[i];
if (Math.min(X, Y) < N && Math.max(X, Y) > N) {
ans = Math.max(ans, height[i]);
}
}
return ans;
}
public static class DC3 {
public int[] sa;
public int[] rank;
public int[] height;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
height = height(nums);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
private int[] height(int[] s) {
int n = s.length;
int[] ans = new int[n];
// Find h [i], k = 0
for (int i = 0, k = 0; i < n; ++i) {
if (rank[i] != 0) {
if (k > 0) {
--k;
}
int j = sa[rank[i] - 1];
while (i + k < n && j + k < n && s[i + k] == s[j + k]) {
++k;
}
// h[i] = k
ans[rank[i]] = k;
}
}
return ans;
}
}