1 topic analysis

Link: 138. Copy the linked list with random pointer - LeetCode (LeetCode CN. Com)

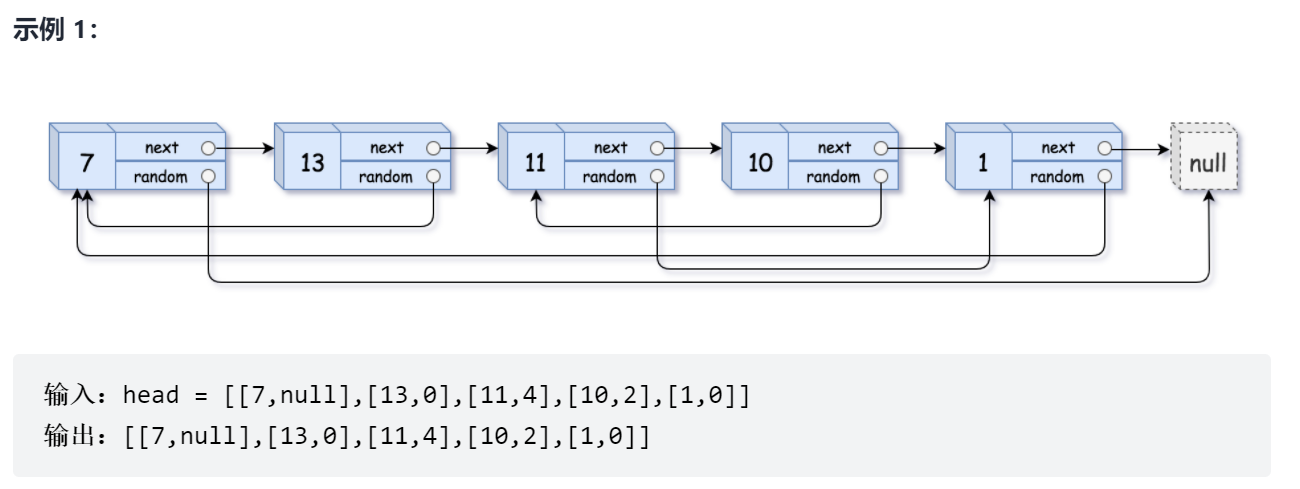
Give you a linked list with a length of n. each node contains an additional random pointer random, which can point to any node or empty node in the linked list.

Construct a deep copy of this linked list. The deep copy should consist of exactly n new nodes, in which the value of each new node is set to the value of its corresponding original node. The next pointer and random pointer of the new node should also point to the new node in the replication linked list, and these pointers in the original linked list and replication linked list can represent the same linked list state. The pointer in the copy linked list should not point to the node in the original linked list.

For example, if there are two nodes X and Y in the original linked list, where x.random -- > y. Then the corresponding two nodes X and Y in the copy linked list also have x.random -- > y.

Returns the header node of the copy linked list.

Use a linked list composed of n # nodes to represent the linked list in input / output. Each node is represented by a [val, random_index]:

Val: one represents node Integer of val.
random_index: the node index pointed by the random pointer (range from # 0 # to # n-1); null if it does not point to any node.
Your code only accepts the head node of the original linked list as the incoming parameter

The structure of the linked list is as follows: in addition to the Next pointer, there is also a random pointer

class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};

Idea 1: hash table (not good at doing)

Idea 2: combine + Split linked list

The key to this problem is how to store the random pointer during copying. Since the random pointer contains subsequent nodes, there must be a complete copy of the original linked list so that the new linked list can be pointed to during construction. The first uses the key value to store the node data location of the original linked list. The second uses a simple structure to store the node data, which makes the pointing method more convenient when building a new linked list.

2 hash table related knowledge

reference material: Data structure Hash table (Hash table)_ Step by step to thousands of miles - CSDN blog_ Hashtable

Common operations of using unordered_map in c + +_ hero_th blog - CSDN blog_ c + + hash table operation

2.1 hash function

Mapping function between numeric value and numeric address

index=H(key)

2.2 construction of hash function

• Direct customization
• Digital analysis
• ......

It should not be too complex and evenly distributed

Hash conflict and its solution

// Establish the mapping of hash table < a, b > from type B to type a
unordered_map<int,int> map; //<string,string>,<char,char>

2.3 operation of hash table

For a given key, calculate the hash address index = H (key)

Add element

map.insert(pair<int,int>(1, 10));
map.insert(pair<int,int>(2, 20));
map[3]=30;
map[4]=40;

lookup

m.end()  //Pointing to the last container of the hash table actually exceeds the scope of the hash table and is empty
m.find(2)  //Find out whether the key value pair with key 2 exists. If not, return m.end()
m.count(3)  //Find the key value pair with key 3 in the hash table and return its quantity. If it is 1, it will be found. If it is not found, it will return 0

ergodic

unordered_map<int, int> count;
for (auto p : count) {
	int front = p.first;   //key
    int end = p.second;   //value
}

3 code implementation

3.1 hash table method

• Initialize Hash list and current node cur
• Traverse the linked list and establish the key value pair of the hash table
• Traverse the linked list for the second time and copy the next and random pointers
• Finally, a hash table with two pointers is returned

class Solution {
public:
    Node* copyRandomList(Node* head) {
        // Non null judgment
        if (head == nullptr) return nullptr;
        // Initialize hash table and node
        Node* cur = head;
        unordered_map<Node*,Node*> map;
        // The first traversal establishes key value pairs
        while (cur != nullptr){
            map[cur] = new Node(cur->val);
            cur = cur->next;
        }
        // The second traversal establishes the next and random pointers
        cur = head;
        while(cur != nullptr){
            map[cur]->next = map[cur->next];
            map[cur]->random = map[cur->random];
            cur = cur->next;
        }
    return map[head];
    }
};

3.2 combined + Split linked list

• After the first traversal, copy the new linked list node after the original linked list
• The second traversal specifies the random pointer of the new linked list node
• The third traversal, through splitting, specifies the next pointer of the new linked list node

This self written code has timed out. The code posted below comes from: Graphical algorithm data structure - LeetBook - LeetCode, the technology growth platform loved by geeks around the world (leetcode-cn.com)

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr) return nullptr;
        Node* cur = head;
        // 1. Copy each node and build a splicing linked list
        while(cur != nullptr) {
            Node* tmp = new Node(cur->val);
            tmp->next = cur->next;
            cur->next = tmp;
            cur = tmp->next;
        }
        // 2. Construct the random direction of each new node
        cur = head;
        while(cur != nullptr) {
            if(cur->random != nullptr)
                cur->next->random = cur->random->next;
            cur = cur->next->next;
        }
        // 3. Split two linked lists
        cur = head->next;
        Node* pre = head, *res = head->next;
        while(cur->next != nullptr) {
            pre->next = pre->next->next;
            cur->next = cur->next->next;
            pre = pre->next;
            cur = cur->next;
        }
        pre->next = nullptr; // Handle the end node of the original linked list separately
        return res;      // Return to the new chain header node
    }
};