Joint search set

summary

• Function: support the rapid merging and searching of collections, with time complexity of O (1)
• Two basic methods: isSameSet: whether two sets belong to the same set; union: merge two sets
• The traditional data structure can not support the rapidity of the two methods at the same time. For example, the linked list structure can support fast consolidation, but it cannot support fast search; Hash table: supports fast lookup, but cannot support fast merge

Solution

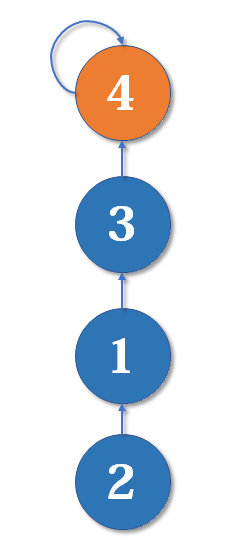
(1) At the beginning, the pointer of each node points to itself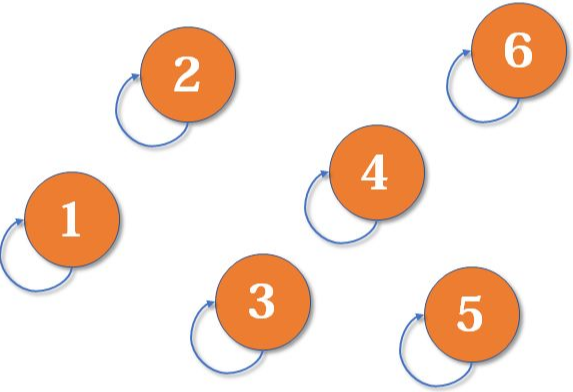
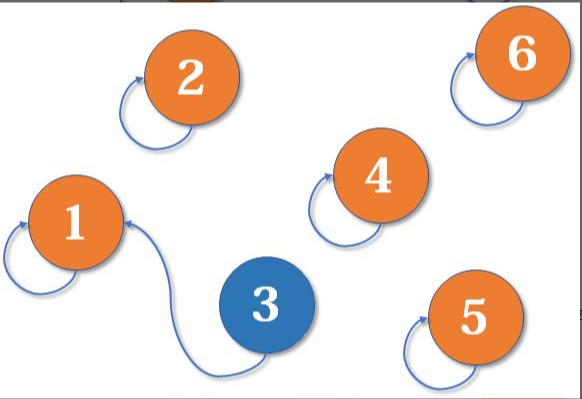
(2) If it points to Union (1, 3): the operation of merging the sets of 1 and 3 will point the pointer of 3 to 1. At this time, 1 is the vertex

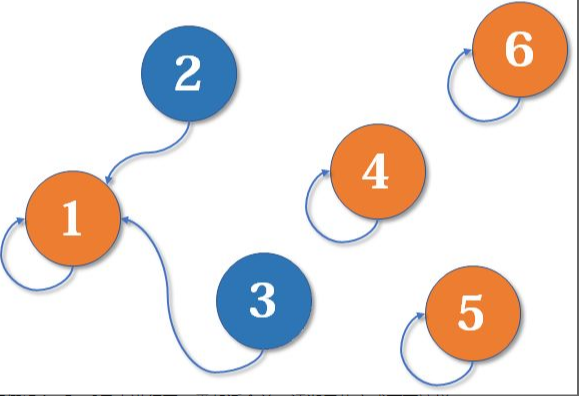
(3) If multiple sets are merged, the vertex with less nodes should point to the vertex with more nodes. For example, union(1,2) is to change the pointer of 2

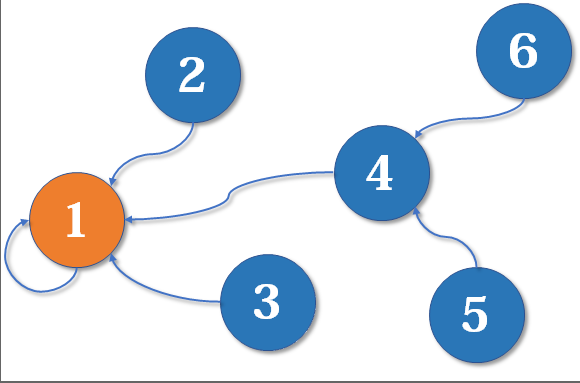
(4) isSameSet: the method can determine whether the top nodes are the same. For example, in the above figure: the return value of isSameSet(2, 6) is false; If in the following figure: the return value of isSameSet(2, 6) is true.

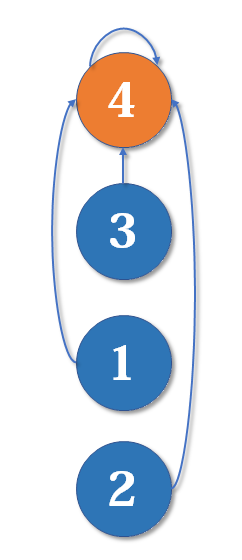
(5) Optimization problem (path compression): if the chain is too long, the time complexity will increase when using isSameSet. Using findHead method, the parent node of each node will eventually become the highest vertex in the process

After using findHead, connect 1 and 2 directly to the vertex

realization

    public static class Element<V>{
        //Packaging of samples to form elements
        //Internal use Element
        //External use V, use of generic classes
        public V value;

        public Element(V value){
         this.value = value;
        }
    }

    public static class UnionFindSet<V>{
        //Joint search set
        public HashMap<V, Element<V>> elementMap;
        //key is the sample, and value is the packaged element corresponding to the sample, which is convenient to judge whether the sample exists
        public HashMap<Element<V>, Element<V>> fatherMap;
        //key is the element and value is the parent element of the element
        public HashMap<Element<V>, Integer> sizeMap;
        //key is the vertex element of a set (representing the set), and value is the size of the set

        public UnionFindSet(List<V> list){
            //Initialization: requires the user to provide a collection
            elementMap = new HashMap<>();
            fatherMap = new HashMap<>();
            sizeMap = new HashMap<>();
            for (V value : list){
                //Traversal set
                //They all start as a set
                Element<V> element = new Element<>(value);
                elementMap.put(value, element);
                fatherMap.put(element, element);
                sizeMap.put(element, 1);
            }
        }

        private Element<V> findHead(Element<V> element){
            //A vertex element of a collection was found
            //And all the parent nodes of the node and its upper nodes are changed into vertex nodes
            Stack<Element<V>> stack = new Stack<>();
            while (element != fatherMap.get(element)){
                //Traverse to vertex element
                stack.push(element);
                element = fatherMap.get(element);
            }
            while (!stack.isEmpty()){
                //Modify this node and the parent node of the node above it to all vertex nodes
                fatherMap.put(stack.pop(), element);
            }
            return element;
        }

        public boolean isSameSet(V a, V b){
            //Judge whether a and b belong to the same set
            if (elementMap.containsKey(a) && elementMap.containsKey(b)){
                //a. b all exist in the set, and judge whether the vertex elements are the same
                return findHead(elementMap.get(a)) == findHead(elementMap.get(b));
            }
            return false;
        }

        public void union(V a, V b){
            if (!elementMap.containsKey(a) || ! elementMap.containsKey(b)){
                //If it does not exist in the set
                return;
            }
            if (isSameSet(a, b)){
                //Belong to the same set
                return;
            }
            //a. Top element of b
            Element<V> aH = findHead(elementMap.get(a));
            Element<V> bH = findHead(elementMap.get(b));
            //a. Distinction between larger sets and smaller sets in b
            Element<V> big = sizeMap.get(aH) >= sizeMap.get(bH) ? aH : bH;
            Element<V> small = big == aH ? bH : aH;
            //Connect smaller vertices to larger vertices
            fatherMap.put(small, big);
            sizeMap.put(big, sizeMap.get(small) + sizeMap.get(big));
            sizeMap.remove(small);
        }
    }

Title: Island problem

thinking

Ergodic matrix turns all connected 1 into 2. There are several islands in the process of turning 2 several times

    public static int countIslands(int[][] land){
        if (land == null || land[0] == null){
            return 0;
        }
        int x = land.length;
        int y = land[1].length;
        int res = 0;
        for (int i = 0; i < x; i++){
            for (int j = 0; j < y; j++){
                if (land[i][j] == 1){
                    //ergodic matrix 
                    res++;
                    infect(land, i, j, x, y);
                }
            }
        }
        return res;
    }

    public static void infect(int[][] land, int i, int j, int x, int y){
        //Change all connected as 1 into 2
        if (i < 0 || i >= x || j < 0 || j >= y || land[i][j] != 1){
            //End condition
            return;
        }
        land[i][j] = 2;
        //Traverse around
        infect(land, i + 1, j, x, y);
        infect(land, i - 1, j, x, y);
        infect(land, i, j + 1, x, y);
        infect(land, i, j - 1, x, y);
    }

    public static void main(String[] args) {
        int[][] land = {{0, 0, 1, 0, 1, 0},
                        {1, 1, 1, 0, 1, 0},
                        {1, 0, 0, 1, 0, 0},
                        {0, 0, 0, 0, 0, 0}};
        System.out.println(countIslands(land));
    }

• Result demonstration:
  
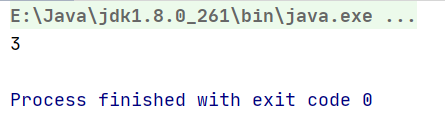
• Time complexity: O (X * Y) x: height of matrix, Y: width of matrix

Advanced: application of joint search set

(1) If the graph is particularly large, divide the graph, and the divided graph can process data in the subgraph at the same time to achieve the effect of parallelism
(2) However, the division map may increase the number of islands
(3) The boundary needs to be processed, and the points to which the boundary becomes in the same connection process are taken as a set
(4) Judge the connected points of the divided subgraph through the line. If the points of the subgraph have adjacent attributes, check whether they belong to a set. If not, the two sets are merged, and the number of graphs is reduced by one