Ordered table

• Function: supports all operations of hash table. Keys are organized in order (hash table is out of order)
• Time complexity: all operations are O(log N) level
• Implementation method:
  (1) Red black tree
  (2)AVL
  (3)SBT
  (4) Skip list
  (1) , (2), (3) all attribute BST (balanced search binary tree)

Search Binary Tree

• There are generally no duplicate items in the search binary tree. You can add data items in the node and record the number of occurrences of node data

• Insert: insert the node from the beginning every time. If the inserted node is smaller than the head node, compare it with its child nodes to the left. If it is larger than the head node, compare it to the right. Repeat the comparison until it reaches the empty node. Insert the node into the empty node

• Delete:
  (1) Leaf node, search the node, record the parent node of the node, and modify the parent node pointer to delete it
  (2) Only the left / right node, search the node, record its parent node and its child nodes, modify the parent node pointer, replace and delete the node with the child node
  (3) Both left and right children have: search the node, replace and delete the node with the rightmost node of the left tree of the node / the leftmost node of the right tree, and then connect the child node of the rightmost / leftmost node with its parent node

• Disadvantages: time complexity is affected by the order in which data is provided

• Change the balance of the tree:
  

• Left rotation: the head node falls to the left
  (1) The p node falls to the left and the right child x becomes the head node
  (2) p becomes the left child of x
  (3) Give the left child of x to p and become the right child of p
  

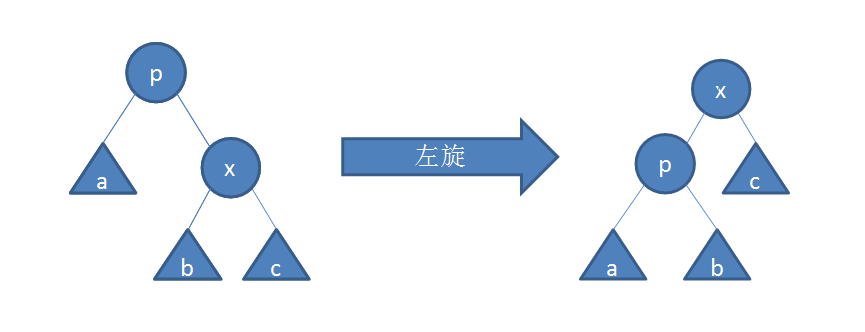
		public void leftRotate(Node cur) {
			Node right = cur.r;
			cur.r = right.l;
			right.l = cur;
		}

• Right rotation: the head node falls to the left
  (1) The p node falls to the right and the left child x becomes the head node
  (2) p becomes the right child of x
  (3) Give the right child of x to p and become the left child of p
  

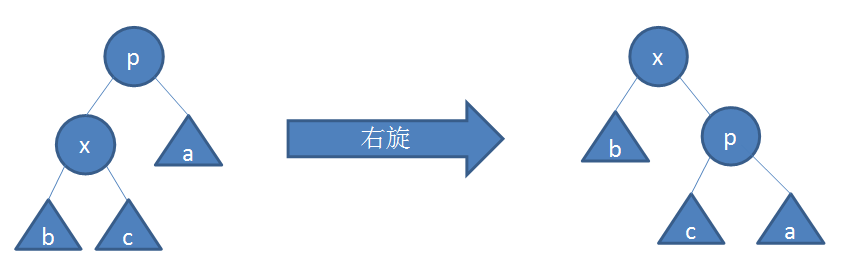
	public Node rightRotate(Node cur) {
			Node left = cur.l;
			cur.l = left.r;
			left.r = cur;
		}

AVL

• Balance requirements: the left and right subtrees are AVL, and the decision value of the height difference between the left and right subtrees is less than or equal to 1
• Check of balance:
  (1) Add node: judge the balance from the position of the added node and upward
  (2) Delete node: start from the position of the deleted node and judge the balance upward. When deleting a node with both left and right nodes, start from replacing the parent node of the node
• There are four situations in which the balance will be broken: Skill: make the middle value of the three nodes as the head node to adjust
  (1) LL: the left side of the left tree breaks the balance. x is the middle value. Make x as the head node, which is the right rotation of y
  
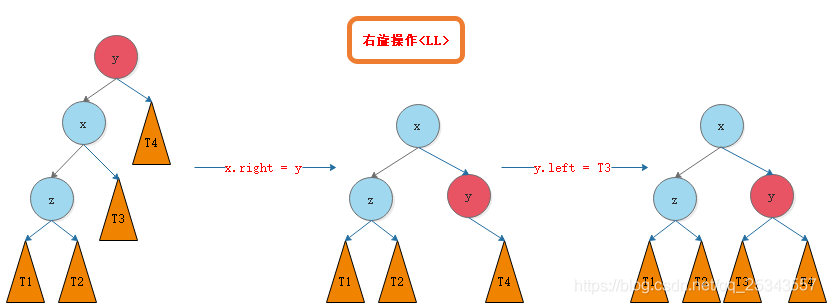
  (2) RR: the right side of the right tree breaks the balance. x is the middle value. Make x as the head node, which is the left rotation of y
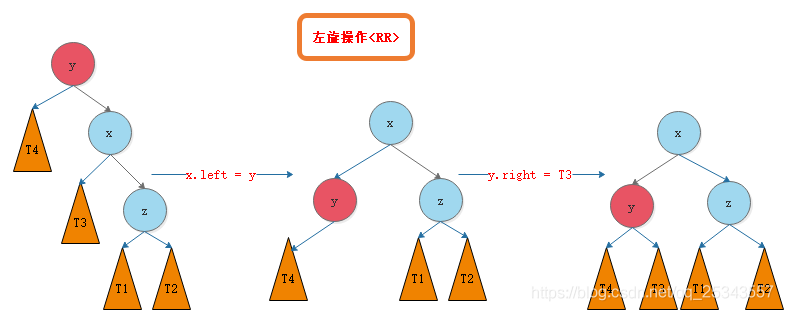  (3) LR: the right side of the left tree breaks the balance, and z is the middle value. Make z as the head node, rotate x left and then y right
  
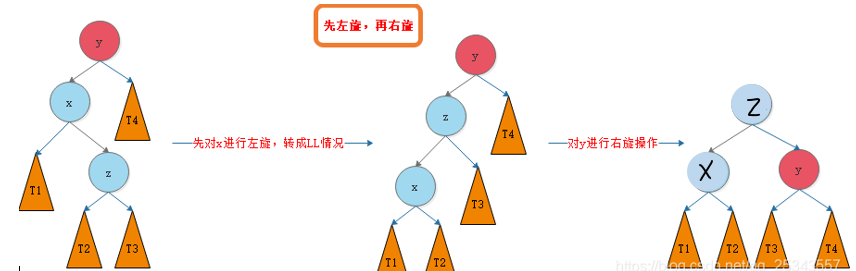
  (4) RL: the left side of the right tree breaks the balance, and z is the middle value. Make z as the head node, rotate x right and then y left
  

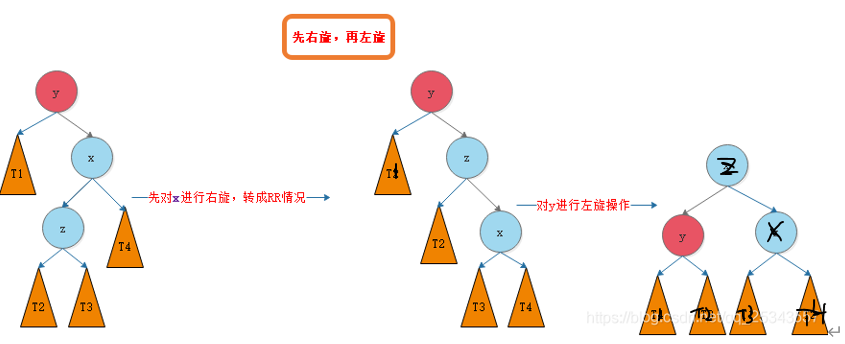
	public static class AVLNode<K extends Comparable<K>, V> {
		public K k;
		public V v;
		public AVLNode<K, V> l;
		public AVLNode<K, V> r;
		public int h;

		public AVLNode(K key, V value) {
			k = key;
			v = value;
			h = 1;
		}
	}

	public static class AVLTreeMap<K extends Comparable<K>, V> {
		private AVLNode<K, V> root;
		private int size;

		public AVLTreeMap() {
			root = null;
			size = 0;
		}

		private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {
			AVLNode<K, V> left = cur.l;
			cur.l = left.r;
			left.r = cur;
			cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
			left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;
			return left;
		}

		private AVLNode<K, V> leftRotate(AVLNode<K, V> cur) {
			AVLNode<K, V> right = cur.r;
			cur.r = right.l;
			right.l = cur;
			cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
			right.h = Math.max((right.l != null ? right.l.h : 0), (right.r != null ? right.r.h : 0)) + 1;
			return right;
		}

		private AVLNode<K, V> maintain(AVLNode<K, V> cur) {
			if (cur == null) {
				return null;
			}
			int leftHeight = cur.l != null ? cur.l.h : 0;
			int rightHeight = cur.r != null ? cur.r.h : 0;
			if (Math.abs(leftHeight - rightHeight) > 1) {
				if (leftHeight > rightHeight) {
					int leftLeftHeight = cur.l != null && cur.l.l != null ? cur.l.l.h : 0;
					int leftRightHeight = cur.l != null && cur.l.r != null ? cur.l.r.h : 0;
					if (leftLeftHeight >= leftRightHeight) {
						cur = rightRotate(cur);
					} else {
						cur.l = leftRotate(cur.l);
						cur = rightRotate(cur);
					}
				} else {
					int rightLeftHeight = cur.r != null && cur.r.l != null ? cur.r.l.h : 0;
					int rightRightHeight = cur.r != null && cur.r.r != null ? cur.r.r.h : 0;
					if (rightRightHeight >= rightLeftHeight) {
						cur = leftRotate(cur);
					} else {
						cur.r = rightRotate(cur.r);
						cur = leftRotate(cur);
					}
				}
			}
			return cur;
		}

		private AVLNode<K, V> findLastIndex(K key) {
			AVLNode<K, V> pre = root;
			AVLNode<K, V> cur = root;
			while (cur != null) {
				pre = cur;
				if (key.compareTo(cur.k) == 0) {
					break;
				} else if (key.compareTo(cur.k) < 0) {
					cur = cur.l;
				} else {
					cur = cur.r;
				}
			}
			return pre;
		}

		private AVLNode<K, V> findLastNoSmallIndex(K key) {
			AVLNode<K, V> ans = null;
			AVLNode<K, V> cur = root;
			while (cur != null) {
				if (key.compareTo(cur.k) == 0) {
					ans = cur;
					break;
				} else if (key.compareTo(cur.k) < 0) {
					ans = cur;
					cur = cur.l;
				} else {
					cur = cur.r;
				}
			}
			return ans;
		}

		private AVLNode<K, V> findLastNoBigIndex(K key) {
			AVLNode<K, V> ans = null;
			AVLNode<K, V> cur = root;
			while (cur != null) {
				if (key.compareTo(cur.k) == 0) {
					ans = cur;
					break;
				} else if (key.compareTo(cur.k) < 0) {
					cur = cur.l;
				} else {
					ans = cur;
					cur = cur.r;
				}
			}
			return ans;
		}

		private AVLNode<K, V> add(AVLNode<K, V> cur, K key, V value) {
			if (cur == null) {
				return new AVLNode<K, V>(key, value);
			} else {
				if (key.compareTo(cur.k) < 0) {
					cur.l = add(cur.l, key, value);
				} else {
					cur.r = add(cur.r, key, value);
				}
				cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;
				return maintain(cur);
			}
		}

		// In the cur tree, delete the node represented by the key
		// Return cur to the new head of the tree
		private AVLNode<K, V> delete(AVLNode<K, V> cur, K key) {
			if (key.compareTo(cur.k) > 0) {
				cur.r = delete(cur.r, key);
			} else if (key.compareTo(cur.k) < 0) {
				cur.l = delete(cur.l, key);
			} else {
				if (cur.l == null && cur.r == null) {
					cur = null;
				} else if (cur.l == null && cur.r != null) {
					cur = cur.r;
				} else if (cur.l != null && cur.r == null) {
					cur = cur.l;
				} else {
					AVLNode<K, V> des = cur.r;
					while (des.l != null) {
						des = des.l;
					}
					cur.r = delete(cur.r, des.k);
					des.l = cur.l;
					des.r = cur.r;
					cur = des;
				}
			}
			if (cur != null) {
				cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;
			}
			return maintain(cur);
		}

		public int size() {
			return size;
		}

		public boolean containsKey(K key) {
			if (key == null) {
				return false;
			}
			AVLNode<K, V> lastNode = findLastIndex(key);
			return lastNode != null && key.compareTo(lastNode.k) == 0 ? true : false;
		}

		public void put(K key, V value) {
			if (key == null) {
				return;
			}
			AVLNode<K, V> lastNode = findLastIndex(key);
			if (lastNode != null && key.compareTo(lastNode.k) == 0) {
				lastNode.v = value;
			} else {
				size++;
				root = add(root, key, value);
			}
		}

		public void remove(K key) {
			if (key == null) {
				return;
			}
			if (containsKey(key)) {
				size--;
				root = delete(root, key);
			}
		}

		public V get(K key) {
			if (key == null) {
				return null;
			}
			AVLNode<K, V> lastNode = findLastIndex(key);
			if (lastNode != null && key.compareTo(lastNode.k) == 0) {
				return lastNode.v;
			}
			return null;
		}

		public K firstKey() {
			if (root == null) {
				return null;
			}
			AVLNode<K, V> cur = root;
			while (cur.l != null) {
				cur = cur.l;
			}
			return cur.k;
		}

		public K lastKey() {
			if (root == null) {
				return null;
			}
			AVLNode<K, V> cur = root;
			while (cur.r != null) {
				cur = cur.r;
			}
			return cur.k;
		}

		public K floorKey(K key) {
			if (key == null) {
				return null;
			}
			AVLNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
			return lastNoBigNode == null ? null : lastNoBigNode.k;
		}

		public K ceilingKey(K key) {
			if (key == null) {
				return null;
			}
			AVLNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
			return lastNoSmallNode == null ? null : lastNoSmallNode.k;
		}

	}

SBT(SizeBalancedTree)

• Balance requirements: the size of each subtree shall not be less than the size of its brother subtree, that is, the size of each uncle tree shall not be less than the size of any nephew tree
  
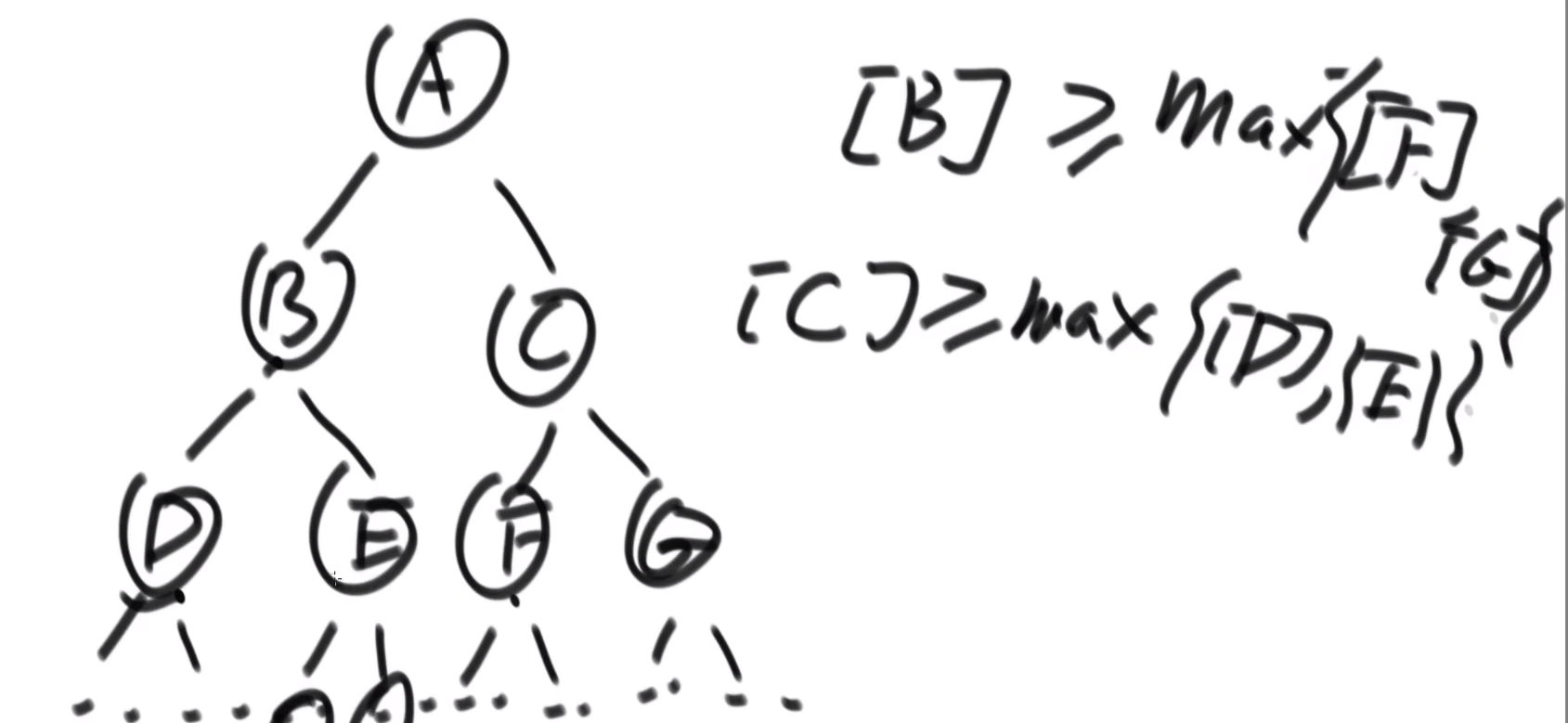
• Check of balance:
  (1) Add node: judge the balance from the position of the added node and upward
  (2) Delete node: start from the position of the deleted node and judge the balance upward. When deleting a node with both left and right nodes, start from replacing the parent node of the node
• There are four situations in which the balance will be broken:
  (1) LL: the left side of the left tree breaks the balance. maintain is a recursive function, and m calls the changed node of the subtree again
  
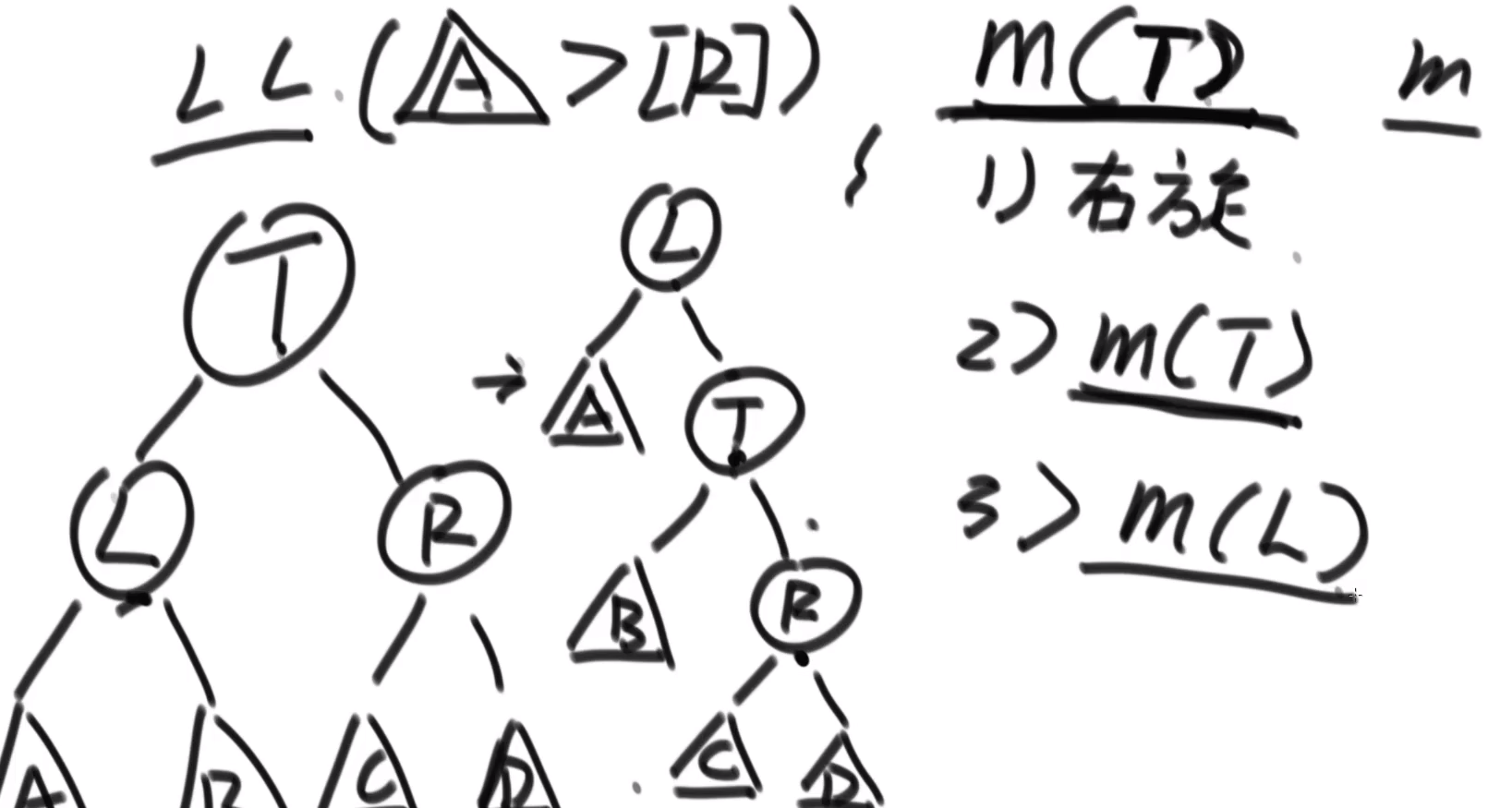
  (2) RR: the right side of the right tree breaks the balance, rotates left, and then calls the m function when the subtree changes
  (3) LR: the right side of the left tree breaks the balance, first left, then right, and then call the m function when the subtree changes
  
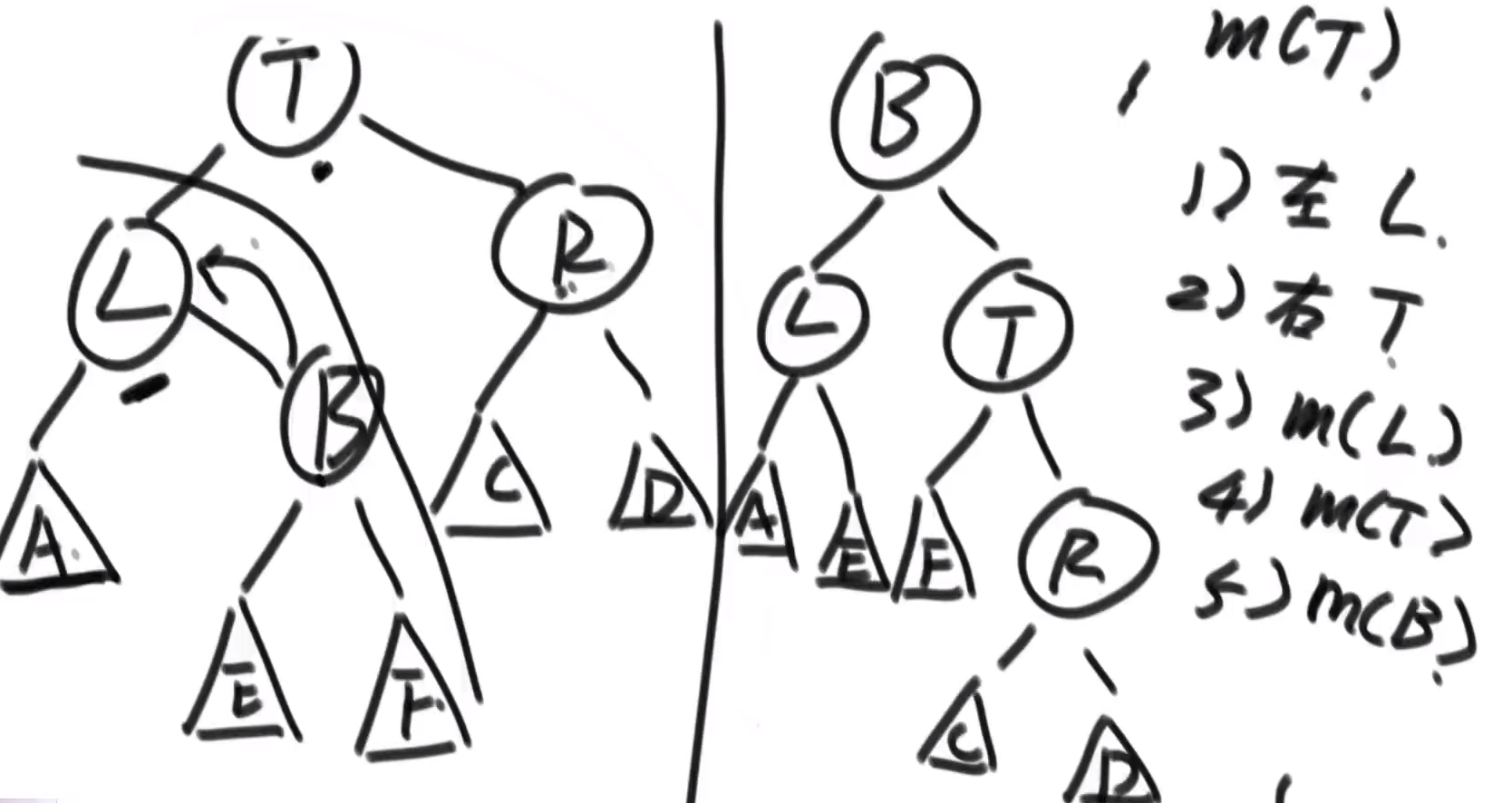
  (4) RL: the left side of the right tree breaks the balance, first right, then left, and then call the m function when the subtree changes

	public static class SBTNode<K extends Comparable<K>, V> {
		public K key;
		public V value;
		public SBTNode<K, V> l;
		public SBTNode<K, V> r;
		public int size; // Number of different key s

		public SBTNode(K key, V value) {
			this.key = key;
			this.value = value;
			size = 1;
		}
	}

	public static class SizeBalancedTreeMap<K extends Comparable<K>, V> {
		private SBTNode<K, V> root;

		private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
			SBTNode<K, V> leftNode = cur.l;
			cur.l = leftNode.r;
			leftNode.r = cur;
			leftNode.size = cur.size;
			cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
			return leftNode;
		}

		private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
			SBTNode<K, V> rightNode = cur.r;
			cur.r = rightNode.l;
			rightNode.l = cur;
			rightNode.size = cur.size;
			cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
			return rightNode;
		}

		private SBTNode<K, V> maintain(SBTNode<K, V> cur) {
			if (cur == null) {
				return null;
			}
			int leftSize = cur.l != null ? cur.l.size : 0;
			int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
			int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
			int rightSize = cur.r != null ? cur.r.size : 0;
			int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
			int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
			if (leftLeftSize > rightSize) {
				cur = rightRotate(cur);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			} else if (leftRightSize > rightSize) {
				cur.l = leftRotate(cur.l);
				cur = rightRotate(cur);
				cur.l = maintain(cur.l);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			} else if (rightRightSize > leftSize) {
				cur = leftRotate(cur);
				cur.l = maintain(cur.l);
				cur = maintain(cur);
			} else if (rightLeftSize > leftSize) {
				cur.r = rightRotate(cur.r);
				cur = leftRotate(cur);
				cur.l = maintain(cur.l);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			}
			return cur;
		}

		private SBTNode<K, V> findLastIndex(K key) {
			SBTNode<K, V> pre = root;
			SBTNode<K, V> cur = root;
			while (cur != null) {
				pre = cur;
				if (key.compareTo(cur.key) == 0) {
					break;
				} else if (key.compareTo(cur.key) < 0) {
					cur = cur.l;
				} else {
					cur = cur.r;
				}
			}
			return pre;
		}

		private SBTNode<K, V> findLastNoSmallIndex(K key) {
			SBTNode<K, V> ans = null;
			SBTNode<K, V> cur = root;
			while (cur != null) {
				if (key.compareTo(cur.key) == 0) {
					ans = cur;
					break;
				} else if (key.compareTo(cur.key) < 0) {
					ans = cur;
					cur = cur.l;
				} else {
					cur = cur.r;
				}
			}
			return ans;
		}

		private SBTNode<K, V> findLastNoBigIndex(K key) {
			SBTNode<K, V> ans = null;
			SBTNode<K, V> cur = root;
			while (cur != null) {
				if (key.compareTo(cur.key) == 0) {
					ans = cur;
					break;
				} else if (key.compareTo(cur.key) < 0) {
					cur = cur.l;
				} else {
					ans = cur;
					cur = cur.r;
				}
			}
			return ans;
		}

		// Now, add a record like (key, value) to the tree headed by cur
		// After adding, cur will be checked and adjusted
		// Return to the new head of the whole tree after adjustment
		private SBTNode<K, V> add(SBTNode<K, V> cur, K key, V value) {
			if (cur == null) {
				return new SBTNode<K, V>(key, value);
			} else {
				cur.size++;
				if (key.compareTo(cur.key) < 0) {
					cur.l = add(cur.l, key, value);
				} else {
					cur.r = add(cur.r, key, value);
				}
				return maintain(cur);
			}
		}

		// In the cur tree, delete the node represented by the key
		// Return cur to the new head of the tree
		private SBTNode<K, V> delete(SBTNode<K, V> cur, K key) {
			cur.size--;
			if (key.compareTo(cur.key) > 0) {
				cur.r = delete(cur.r, key);
			} else if (key.compareTo(cur.key) < 0) {
				cur.l = delete(cur.l, key);
			} else { // cur to be deleted at present
				if (cur.l == null && cur.r == null) {
					// free cur memory -> C++
					cur = null;
				} else if (cur.l == null && cur.r != null) {
					// free cur memory -> C++
					cur = cur.r;
				} else if (cur.l != null && cur.r == null) {
					// free cur memory -> C++
					cur = cur.l;
				} else { // Left and right
					SBTNode<K, V> pre = null;
					SBTNode<K, V> des = cur.r;
					des.size--;
					while (des.l != null) {
						pre = des;
						des = des.l;
						des.size--;
					}
					if (pre != null) {
						pre.l = des.r;
						des.r = cur.r;
					}
					des.l = cur.l;
					des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
					// free cur memory -> C++
					cur = des;
				}
			}
			// cur = maintain(cur);
			return cur;
		}

		private SBTNode<K, V> getIndex(SBTNode<K, V> cur, int kth) {
			if (kth == (cur.l != null ? cur.l.size : 0) + 1) {
				return cur;
			} else if (kth <= (cur.l != null ? cur.l.size : 0)) {
				return getIndex(cur.l, kth);
			} else {
				return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);
			}
		}

		public int size() {
			return root == null ? 0 : root.size;
		}

		public boolean containsKey(K key) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			SBTNode<K, V> lastNode = findLastIndex(key);
			return lastNode != null && key.compareTo(lastNode.key) == 0 ? true : false;
		}

		// (key, value) put - > add and change value in the ordered table
		public void put(K key, V value) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			SBTNode<K, V> lastNode = findLastIndex(key);
			if (lastNode != null && key.compareTo(lastNode.key) == 0) {
				lastNode.value = value;
			} else {
				root = add(root, key, value);
			}
		}

		public void remove(K key) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			if (containsKey(key)) {
				root = delete(root, key);
			}
		}

		public K getIndexKey(int index) {
			if (index < 0 || index >= this.size()) {
				throw new RuntimeException("invalid parameter.");
			}
			return getIndex(root, index + 1).key;
		}

		public V getIndexValue(int index) {
			if (index < 0 || index >= this.size()) {
				throw new RuntimeException("invalid parameter.");
			}
			return getIndex(root, index + 1).value;
		}

		public V get(K key) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			SBTNode<K, V> lastNode = findLastIndex(key);
			if (lastNode != null && key.compareTo(lastNode.key) == 0) {
				return lastNode.value;
			} else {
				return null;
			}
		}

		public K firstKey() {
			if (root == null) {
				return null;
			}
			SBTNode<K, V> cur = root;
			while (cur.l != null) {
				cur = cur.l;
			}
			return cur.key;
		}

		public K lastKey() {
			if (root == null) {
				return null;
			}
			SBTNode<K, V> cur = root;
			while (cur.r != null) {
				cur = cur.r;
			}
			return cur.key;
		}

		public K floorKey(K key) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			SBTNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
			return lastNoBigNode == null ? null : lastNoBigNode.key;
		}

		public K ceilingKey(K key) {
			if (key == null) {
				throw new RuntimeException("invalid parameter.");
			}
			SBTNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
			return lastNoSmallNode == null ? null : lastNoSmallNode.key;
		}

	}

Red black tree

• summary:
  (1) Each node is either red or black
  (2) Leaf node: it is not a node without left and right children, but an empty node
  (3) Head and leaf nodes must be black
  (4) Any two red nodes cannot be adjacent
  (5) All paths from any node to each leaf node have the same number of black nodes
• Effect: the longest possible path from root to leaf is no more than twice as long as the shortest possible path. The result is that the tree is roughly balanced
  

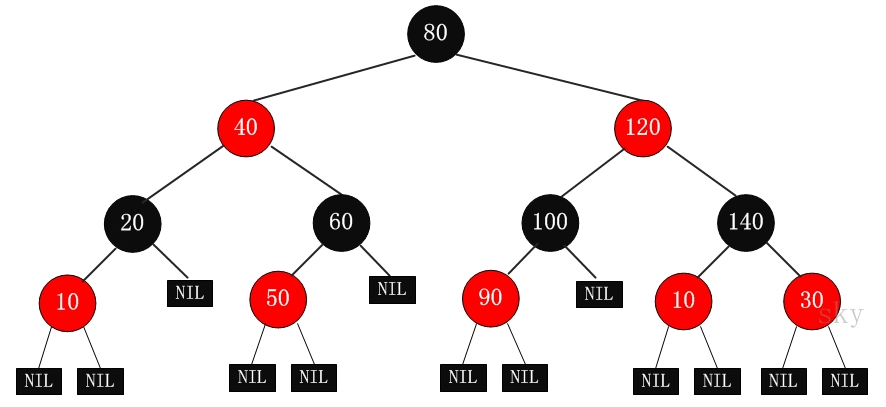
AVL, SBT, red black tree comparison

• generality
  (1) All search Binary Trees
  (2) Insert, delete and query (all queries) are based on search binary tree
  (3) The basic movements of using adjustment are only left rotation and right rotation
  (4) When inserting or deleting, start from the bottom affected node and check the balance of the nodes on the upward path
  (5) Because only O(1) is checked and adjusted for each node of an upward path, O(logN) can be achieved
• difference
  (1) The constraints of balance are different: AVL tree is the most strict, SBT tree is slightly loose, and red black tree is the most loose (balance: the scale of left and right subtrees is roughly the same)
  (2) Because the constraints of balance are different, there is a constant time difference in the adjustment of inserting and deleting balance changes

Skip list

• summary:
  (1) At the beginning, there is a default node (linked list, whose key is the smallest) head
  (2) Every departure starts from the head
  (3) Add a node, which randomly generates a height. If the height of the head node is smaller than it, the head node will expand the height (only the head node can be expanded, and the height of the head node should be the highest)
  (4) Connect the pointer in the head node to the corresponding layer of the connection node
  
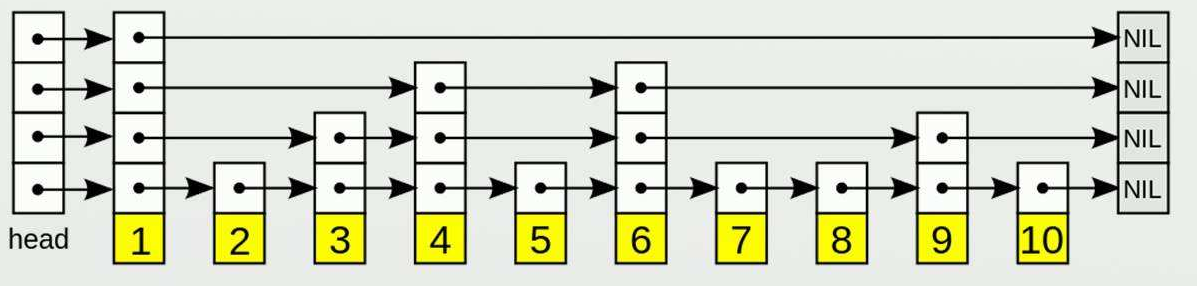
  As shown in the figure: it is a jump table with 10 data. The random height generated by 1 is 4, and the random height generated by 2 is 1
• basic operation
  
  (1) Search: find the highest level through the head, and directly compare the elements corresponding to the highest level. If the highest level cannot, jump to the next level. Because the whole is orderly, the search of nodes can be reduced
  For example: find 40. The top layer starts with 20 and is less than 40, so you can skip 2, 10 and 15. Next time, you can directly find 100, greater than, from 20 to the next layer 50, greater than, and then find 40 on the next layer
  (2) Insert: set the number of layers corresponding to the inserted element, determine the insertion position through search, and use the insertion layer to change the connection of nodes
  Example: insert 70, corresponding to 2 layers
  
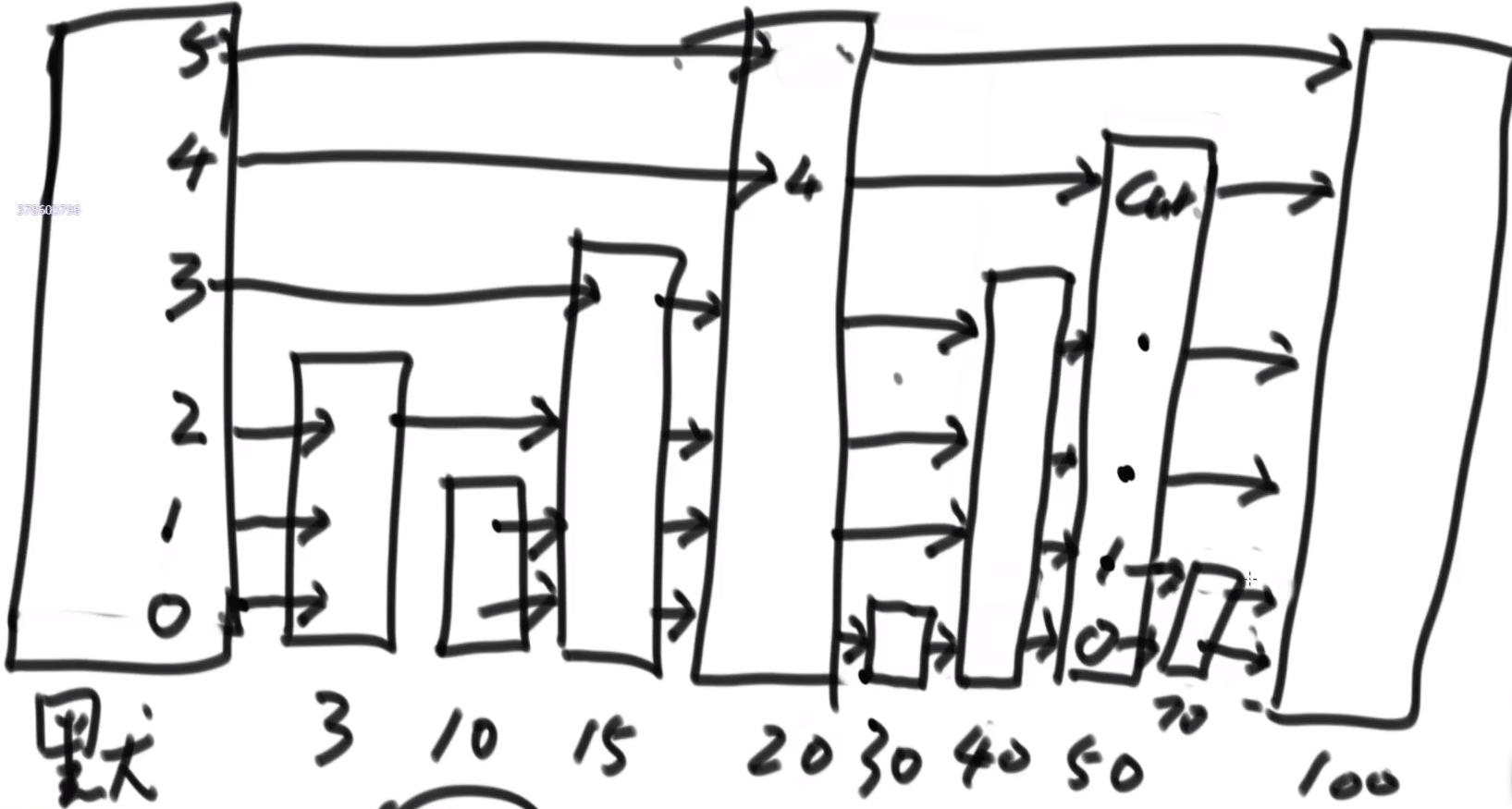
  (3) Delete: search first, and directly ignore the node before the node to be deleted and connect it with the following node
• Complexity:
  (1) Trade space for time
  (2) If a linked list has n nodes, if every two nodes extract one node to establish an index, the number of nodes of the first level index is about n/2, the number of nodes of the second level index is about n/4, and so on. The number of nodes of the M-level index is about n/(2^m). We can see that this is an equal ratio sequence
  (3) Therefore, the spatial complexity of the jump table is O(n)
  (4) The height calculation of the hop table is similar to the full binary tree: the height of the entire hop table is log(n), and the time complexity of the query of the hop table is O(logn)

	public static class SkipListNode<K extends Comparable<K>, V> {
		public K key;
		public V val;
		public ArrayList<SkipListNode<K, V>> nextNodes;

		public SkipListNode(K k, V v) {
			key = k;
			val = v;
			nextNodes = new ArrayList<SkipListNode<K, V>>();
		}

		// When traversing, if it is null(next == null) traversed to the right, the traversal ends
		// Head (null), the null of the head node, which is considered to be the smallest
		// Node - > header, node (null, "") node isKeyLess(!null)  true
		// Is the key in node smaller than otherKey? true, not false
		public boolean isKeyLess(K otherKey) {
			//  otherKey == null -> false 
			return otherKey != null && (key == null || key.compareTo(otherKey) < 0);
		}

		public boolean isKeyEqual(K otherKey) {
			return (key == null && otherKey == null)
					|| (key != null && otherKey != null && key.compareTo(otherKey) == 0);
		}

	}

	public static class SkipListMap<K extends Comparable<K>, V> {
		private static final double PROBABILITY = 0.5; // < 0.5 continue, > = 0.5 stop
		private SkipListNode<K, V> head;
		private int size;
		private int maxLevel;

		public SkipListMap() {
			head = new SkipListNode<K, V>(null, null);
			head.nextNodes.add(null); // 0
			size = 0;
			maxLevel = 0;
		}

		// From the top, all the way down,
		// Finally, find the rightmost node of < key in layer 0
		private SkipListNode<K, V> mostRightLessNodeInTree(K key) {
			if (key == null) {
				return null;
			}
			int level = maxLevel;
			SkipListNode<K, V> cur = head;
			while (level >= 0) { // Jump from top to bottom
				//  cur  level  -> level-1
				cur = mostRightLessNodeInLevel(key, cur, level--);
			}
			return cur;
		}

		// In the level layer, how to move to the right
		// Now the node is cur, and you come to the level layer of cur. On the level layer, find the last node < key and return
		private SkipListNode<K, V> mostRightLessNodeInLevel(K key, 
				SkipListNode<K, V> cur, 
				int level) {
			SkipListNode<K, V> next = cur.nextNodes.get(level);
			while (next != null && next.isKeyLess(key)) {
				cur = next;
				next = cur.nextNodes.get(level);
			}
			return cur;
		}

		public boolean containsKey(K key) {
			if (key == null) {
				return false;
			}
			SkipListNode<K, V> less = mostRightLessNodeInTree(key);
			SkipListNode<K, V> next = less.nextNodes.get(0);
			return next != null && next.isKeyEqual(key);
		}

		// Add and change value
		public void put(K key, V value) {
			if (key == null) {
				return;
			}
			// On layer 0, the rightmost one, < key's node - > key
			SkipListNode<K, V> less = mostRightLessNodeInTree(key);
			SkipListNode<K, V> find = less.nextNodes.get(0);
			if (find != null && find.isKeyEqual(key)) {
				find.val = value;
			} else { // find == null   8   7   9
				size++;
				int newNodeLevel = 0;
				while (Math.random() < PROBABILITY) {
					newNodeLevel++;
				}
				// newNodeLevel
				while (newNodeLevel > maxLevel) {
					head.nextNodes.add(null);
					maxLevel++;
				}
				SkipListNode<K, V> newNode = new SkipListNode<K, V>(key, value);
				for (int i = 0; i <= newNodeLevel; i++) {
					newNode.nextNodes.add(null);
				}
				int level = maxLevel;
				SkipListNode<K, V> pre = head;
				while (level >= 0) {
					// In the level layer, find the rightmost node < key
					pre = mostRightLessNodeInLevel(key, pre, level);
					if (level <= newNodeLevel) {
						newNode.nextNodes.set(level, pre.nextNodes.get(level));
						pre.nextNodes.set(level, newNode);
					}
					level--;
				}
			}
		}

		public V get(K key) {
			if (key == null) {
				return null;
			}
			SkipListNode<K, V> less = mostRightLessNodeInTree(key);
			SkipListNode<K, V> next = less.nextNodes.get(0);
			return next != null && next.isKeyEqual(key) ? next.val : null;
		}

		public void remove(K key) {
			if (containsKey(key)) {
				size--;
				int level = maxLevel;
				SkipListNode<K, V> pre = head;
				while (level >= 0) {
					pre = mostRightLessNodeInLevel(key, pre, level);
					SkipListNode<K, V> next = pre.nextNodes.get(level);
					// 1) In this layer, the next pre is the key
					// 2) In this layer, the next key of pre is > key to delete
					if (next != null && next.isKeyEqual(key)) {
						// free delete node memory -> C++
						// level : pre -> next(key) -> ...
						pre.nextNodes.set(level, next.nextNodes.get(level));
					}
					// There is only one node in the level layer, which is the default node head
					if (level != 0 && pre == head && pre.nextNodes.get(level) == null) {
						head.nextNodes.remove(level);
						maxLevel--;
					}
					level--;
				}
			}
		}

		public K firstKey() {
			return head.nextNodes.get(0) != null ? head.nextNodes.get(0).key : null;
		}

		public K lastKey() {
			int level = maxLevel;
			SkipListNode<K, V> cur = head;
			while (level >= 0) {
				SkipListNode<K, V> next = cur.nextNodes.get(level);
				while (next != null) {
					cur = next;
					next = cur.nextNodes.get(level);
				}
				level--;
			}
			return cur.key;
		}

		public K ceilingKey(K key) {
			if (key == null) {
				return null;
			}
			SkipListNode<K, V> less = mostRightLessNodeInTree(key);
			SkipListNode<K, V> next = less.nextNodes.get(0);
			return next != null ? next.key : null;
		}

		public K floorKey(K key) {
			if (key == null) {
				return null;
			}
			SkipListNode<K, V> less = mostRightLessNodeInTree(key);
			SkipListNode<K, V> next = less.nextNodes.get(0);
			return next != null && next.isKeyEqual(key) ? next.key : less.key;
		}

		public int size() {
			return size;
		}

	}