summary
- Premise of use: if the goal of problem solving is rule S, the solving process can be determined as each answer of the subtree with each node as the head node under rule S, and the final answer must be in it
- Routine steps:
(1) In the subtree with a node x as the head node, analyze the possibilities (difficulties) of the answer, and this analysis considers the possibilities from the perspective of the left subtree of X, the right subtree of X and the whole tree of X
(2) List all required information according to the possibility analysis in (1)
(3) Merge the information of (2), put forward the same requirements for the left and right trees, and write the information structure
(4) Design a recursive function, which is the answer when X is the head node, including designing a recursive basecase, directly obtaining all the information of the left and right trees by default (the construction of black boxes), and integrating the possibilities, And return to the information structure of the third step (disassembly of black box) (in the following topics, the use of black box is described in more detail in the recursive function design part)
Topic 1: the maximum distance between binary tree nodes

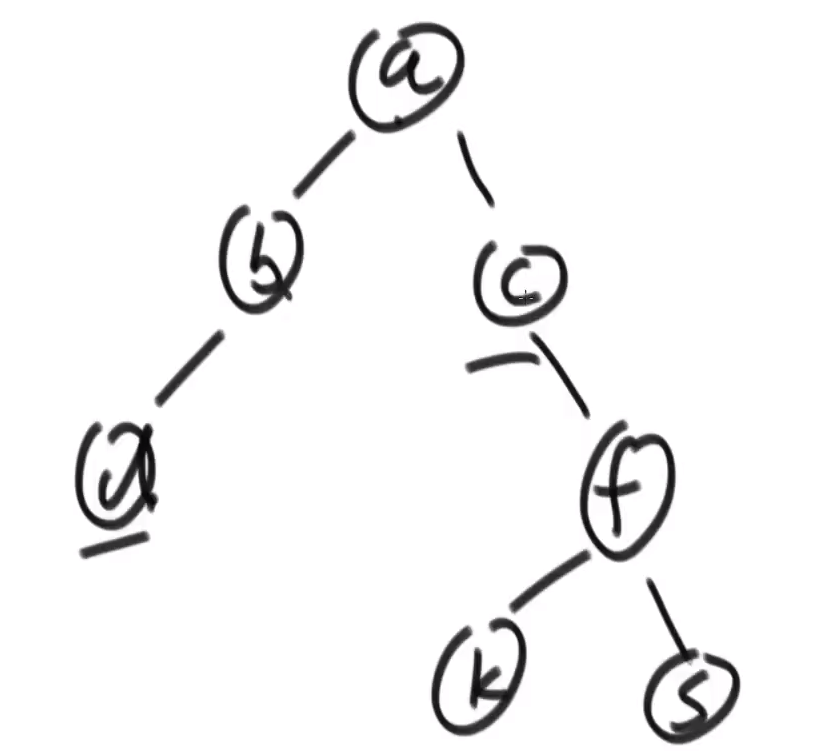
As shown in the figure: the distance from a to b is 2, the distance from d to c is 4, and the distance from d to k is 6
- Enumeration (violence) idea: any two nodes can directly calculate the direct distance. All nodes can find the maximum value after calculating the distance between any two nodes, but the time complexity is too high
- Tree dp idea:
1 possibility analysis: two categories, whether X participates in the maximum value
(1) X participation, from the lowest end of X left tree to the lowest end of X right tree, the height of left tree + 1 + the height of right tree
(2) X does not participate. It is solved inside the left and right trees. The maximum distance of the left tree and the maximum distance of the right tree
(3) The maximum length of X is: the maximum distance of the left tree; Maximum distance of right tree; The height of the left tree + 1 + the height of the right tree, the maximum of the three
2 information requirements
(1) Case 1: height of left tree, height of right tree
(2) Case 2: the maximum distance of the left tree and the maximum distance of the right tree
(3) To sum up: the information structure that the subtree needs to return to the parent node: maximum distance and height
3 recursive function design
(1) basecase: information returned when the node is empty (0, 0)
(2) Construction of black box: it is assumed that the desired information structure of left and right subtrees is obtained directly
(3) Dismantling the black box: how to integrate the information structure of a specific node after obtaining the information of the left and right subtrees
public static class Node{
//Tree node
public int value;
public Node left;
public Node right;
public Node(int date){
//initialization
this.value = date;
}
}
public static class Info{
//Information return type
public int maxDistance;
public int height;
public Info(int maxDistance, int height){
this.maxDistance = maxDistance;
this.height = height;
}
}
public static int maxDistance(Node head){
//Maximum distance function
return process(head).maxDistance;
}
public static Info process(Node x){
//Find the Info information of the whole tree with X as the head
if (x == null){
//basecase
return new Info(0, 0);
}
//Construction of black box: recursively call to get the Info information of left and right subtrees
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
//Information integration
//Maximum distance provided by left and right trees without X
int leftDistance = leftInfo.maxDistance;
int rightDistance = rightInfo.maxDistance;
//Maximum distance with X
int xDistance = leftInfo.height + 1 + rightInfo.height;
//Disassemble the black box: give the solution of the node information
int maxDistance = Math.max(xDistance, Math.max(leftDistance, rightDistance));
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
return new Info(maxDistance, height);
}
Topic 2: queuing maximum happiness (multi tree problem)

- Tree dp idea:
1 possibility analysis: two categories, whether X participates in the maximum value
(1) X participation, maximum value: the value of X + the maximum value provided when the vertices of X subtree do not participate
(2) X does not participate, maximum value: 0 + max (subtree vertices participate, subtree vertices do not participate)
(3) Maximum value: the maximum value of X participating and X not participating
2 information requirements
(1) Case 1: maximum value of head node participation
(2) Case 2: the maximum value that the head node does not participate in
(3) To sum up: the information structure that the subtree needs to return to the parent node: (the subtree vertex participates, and the subtree vertex does not participate)
3 recursive function design
(1) basecase: when the node is a leaf node, it returns (the value of the node, 0)
(2) Construction of black box: it is assumed that the desired information structure of all subtrees is obtained directly
(3) Dismantling the black box: how to integrate the information structure of a specific node after obtaining all the subtree information
public static class Employee{
//Employee information
public int happy; //Happiness requires maximum
public List<Employee> nexts; //Child node
public Employee(int date){
//initialization
this.happy = date;
}
}
public static class Info{
//Information return type
public int xMaxHappy; //x node participation
public int maxHappy; //x not participating
public Info(int xMaxHappy, int maxHappy){
this.xMaxHappy = xMaxHappy;
this.maxHappy = maxHappy;
}
}
public static int maxHappy(Employee boss){
//Maximum happiness
Info headInfo = process(boss);
return Math.min(headInfo.xMaxHappy, headInfo.maxHappy);
}
public static Info process(Employee x){
//Returns the Info information of x
if (x.nexts.isEmpty()){
//basecase
return new Info(x.happy, 0);
}
int xMaxHappy = x.happy;
int maxHappy = 0;
for (Employee next : x.nexts){
//Traversing the subtree of x
//Structure of black box
Info nextInfo = process(next);
//Remove the black box
xMaxHappy += nextInfo.maxHappy;
maxHappy += Math.max(nextInfo.xMaxHappy, nextInfo.maxHappy);
}
return new Info(xMaxHappy, maxHappy);
}
Topic 3: judge whether it is a full binary tree
- Tree dp idea:
1 possibility analysis: depth H, number of nodes N
(1) Is a full binary tree: N == 2 ^ H - 1
(2) Not full binary tree: n= 2 ^H - 1
2 information requirements
(1) H of the parent node = the larger value of H in the left and right subtrees + 1
(2) N of parent node = left n + right n
(3) The information structure that the subtree needs to return to the parent node: depth, node tree
3 recursive function design
(1) basecase: if the node is empty, return (0, 0)
(2) Construction of black box: it is assumed that the desired information structure of left and right subtrees is obtained directly
(3) Dismantling the black box: how to integrate the information structure of a specific node after obtaining all the subtree information
public static class Node{
int value;
Node left;
Node right;
public Node(int date){
this.value = date;
}
}
public static class Info{
public int height; //Height of tree
public int num; //Number of nodes
public Info(int height, int num){
//initialization
this.height = height;
this.num = num;
}
}
public static boolean isFull(Node head){
//Judge whether it is a full binary tree
Info headInfo = process(head);
//1 < < x, x power of 2
return headInfo.num == (1 << headInfo.height - 1);
}
public static Info process(Node x){
//Returns the Info information of x
if (x == null){
//basecase
return new Info(0, 0);
}
//Construction of black box
Info left = process(x.left);
Info right= process(x.right);
//Disassemble the black box
int height = Math.max(left.height, right.height) + 1;
int num = left.num + right.num + 1;
return new Info(height, num);
}
Topic 4: judge whether it is a balanced binary tree
- Tree dp idea:
1 possibility analysis:
(1) X balance: left and right are balanced binary trees, and | left height - right height | < = 1
(2) X is unbalanced, just one that does not meet the balance
2 information requirements
(1) Whether the left and right subtrees are balanced
(2) Height of left and right trees
(3) The information structure that the subtree needs to return to the parent node: whether it is balanced and high
3 recursive function design
(1) basecase: if the node is empty, return (true, 0)
(2) Construction of black box: it is assumed that the desired information structure of left and right subtrees is obtained directly
(3) Dismantling the black box: how to integrate the information structure of a specific node after obtaining all the subtree information
public static class Node{
int value;
Node left;
Node right;
public Node(int date){
this.value = date;
}
}
public static class Info {
//Info
public boolean isBalanced; //Is the tree balanced
public int height;
public Info(boolean isBalanced, int height){
//Constructor
this.isBalanced = isBalanced;
this.height = height;
}
}
public static boolean isBalancedTree(Node head){
return process(head).isBalanced;
}
public static Info process(Node x){
//Returns the Info information of x
if (x == null){
//basecase
return new Info(true, 0);
}
//Black box structure
Info leftTree = process(x.left);
Info rightTree= process(x.right);
//Disassemble the black box
int height = Math.max(leftTree.height, rightTree.height) + 1;
boolean isBalanced = leftTree.isBalanced && rightTree.isBalanced
&& Math.abs(leftTree.height - rightTree.height) < 2;
return new Info(isBalanced, height);
}
Topic 5: judge whether it is a binary sort tree
- Tree dp idea:
1 possibility analysis:
(1) X is: left Max < head Value < right min, left and right are binary sort trees
(2) X is not, the condition is not met
2 information requirements
(1) Whether the left and right subtrees are binary sort trees
(2) Left max, min; Right min, Max
(1) The information structure that the subtree needs to return to the parent node: whether it is a binary sort tree, the left and right max, min
3 recursive function design
(1) basecase: the node is empty. Because max and min are not easy to set, null is returned directly
(2) The information structure of the left and right sub boxes is constructed directly
(3) Dismantling the black box: how to integrate the information structure of a specific node after obtaining all the subtree information
public static class Node{
int value;
Node left;
Node right;
public Node(int date){
this.value = date;
}
}
public static class Info {
//info
public boolean isBST; //Is the tree a search tree
public int min; //Minimum value of tree
public int max; //Maximum value of the tree
public Info(boolean isBST, int min, int max){
//Constructor
this.isBST = isBST;
this.min = min;
this.max = max;
}
}
public static boolean isBSTree(Node head){
return process(head).isBST;
}
public static Info process(Node x){
//Return Info of x
if (x == null){
//The min and max of the empty tree are not easy to set, so they are directly set to null
return null;
}
//Black box structure
Info leftTree = process(x.left); //Recursive call
Info rightTree= process(x.right);
//Disassemble the black box
int min = x.value; //Setting of min and max
int max = x.value;
if (leftTree != null){
//Left subtree is empty
min = Math.min(min, leftTree.min);
max = Math.max(max, leftTree.max);
}
if (rightTree != null){
//The right subtree is empty
min = Math.min(min, rightTree.min);
max = Math.max(max, rightTree.max);
}
boolean isBST = true; //isBST settings
if (leftTree != null && (leftTree.isBST || leftTree.max > x.value)){
//Under the condition that the left is not empty: the left subtree is not a search binary tree or the left Max > head, value
//Not satisfying search Binary Tree
isBST = false;
}
if (rightTree != null && (rightTree.isBST || rightTree.min < x.value)){
isBST = false;
}
return new Info(isBST, min, max);
}