1, Experimental purpose
Master the basic idea of dynamic programming and the basic steps to solve the problem, understand the relationship and difference between dynamic programming and divide and conquer, and compare the time complexity of two algorithm design strategies to solve the same problem.

2, Experimental requirements
Use c + + language to solve the optimal scheduling problem of independent tasks with dynamic programming algorithm, analyze the time complexity, and experience the basic ideas and steps of dynamic programming algorithm to solve the problem.

3, Experimental principle
The optimal scheduling problem of independent tasks has the property of optimal substructure. First calculate m=max{max{ai},max{bi} and let the Boolean p(i, j, k) indicate that the first k jobs can be completed within the time of processor A not exceeding i and processor B not exceeding j. The recursive equation is as follows:

p(i，j，k)=p( i-ak，j，k-1 )|p( i，j-bk，k-1 )

Then the shortest time is min{max{i, j}.

4, Experimental process (steps)

#include "bits/stdc++.h"
using namespace std;
int n, m, mn, MiniTime;
int *a;
int *b;
int ***p;
void Make3DArray(int ***&x, int rows, int cols, int k) {//Create a 3D array
    x = new int **[rows];
    for (int i = 0; i < rows; i++) {
        x[i] = new int *[cols];
        for (int j = 0; j < cols; j++)
            x[i][j] = new int[k];
    }
}
void Free3DArray(int ***&x, int rows, int cols, int k) {//Release 3D array
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            free(x[i][j]);
        }
        free(x[i]);
    }
    free(x);
}
void init() {//Initialization, input data, create array
    cin >> n;
    m = 0;
    a = new int[n];
    b = new int[n];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        if (a[i] > m)
            m = a[i];
    }
    for (int i = 0; i < n; i++) {
        cin >> b[i];
        if (b[i] > m)
            m = b[i];
    }
    mn = m * n;
    Make3DArray(p, mn + 1, mn + 1, n + 1);
}
void dtgh() {//Execute dynamic programming algorithm
    int i, j, k;
    //Initialize 3D array
    for (i = 0; i <= mn; i++) {
        for (j = 0; j <= mn; j++) {
            p[i][j][0] = true;
            for (k = 1; k <= n; k++)
                p[i][j][k] = false;
        }
    }
    for (k = 1; k <= n; k++) {//Execute dynamic programming recursion
        for (i = 0; i <= mn; i++) {
            for (j = 0; j <= mn; j++) {
                if (i - a[k - 1] >= 0)
                    p[i][j][k] = p[i - a[k - 1]][j][k - 1];
                if (j - b[k - 1] >= 0)
                    p[i][j][k] = (p[i][j][k] || p[i][j - b[k - 1]][k - 1]);
            }
        }
    }
    for (i = 0, MiniTime = mn; i <= mn; i++) { //Calculate the optimal value
        for (j = 0; j <= mn; j++) {
            if (p[i][j][n]) {
                int tmp = (i > j) ? i : j;
                if (tmp < MiniTime)
                    MiniTime = tmp;
            }
        }
    }
    cout << "Minimum time required to complete all operations:"<<MiniTime << endl;
}
void free() {//Free up space requested
    Free3DArray(p, mn + 1, mn + 1, n + 1);
    free(a);
    free(b);
}
int main() {//main program
    init();
    dtgh();
    free();
    return 0;
}

5, Operation results
case1:

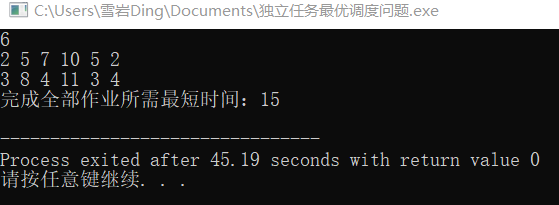
case2:

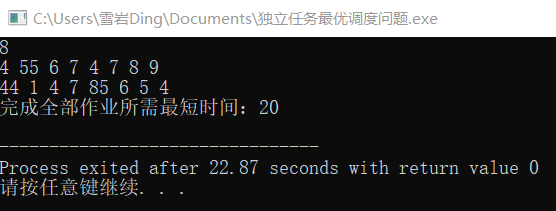
6, Experimental analysis and discussion
1. This experiment is more difficult than the last one. The difficulty is how to get the state transition equation: p(i, J, K) = p(i-Ak, J, k-1) |p(i, j-bk, k-1)? Later, after careful thinking, I understood the meaning, and it was easier to write code;
2. The difficulty 2 of this experiment lies in the understanding that the shortest time is min{max{i,j}. To meet the requirements of completing on A first and then on B, we must find min{max{i,j};

7, Experimental features and experience
Experimental features: the optimal scheduling problem of independent tasks in this experiment belongs to the classical dp problem, and the optimal solution is found through the state transition equation.
Experimental experience: this experiment is difficult, but through this experiment, I have a clearer understanding and more skilled grasp of dp thought, especially the meaning of state transition equation.