Execution code see GitHub
https://github.com/GloryXu/algorithm/tree/master/src/main/java/com/redsun/algorithm/subarraysum

Stroll forum inadvertently found an algorithm post, didn't come up with a better solution for a while, searched, sorted out.

brute force

    @Override
    public void execute() {
        for (int i = 0; i < arr.length; i++) {
            // Traverse all subarrays starting with i
            for (int j = i; j < arr.length; j++) {
                int thisSum = 0;

                // Cumulative sum
                for (int k = i; k <= j; k++) {
                    thisSum += arr[k];
                }
                if (thisSum > maxSum) {
                    // Record the position and length of the largest subarray
                    maxSum = thisSum;
                    start = i;
                    end = j;
                }
            }
        }
    }

The outer two loops, the inner one loop sum, then compare, and finally find a largest sub array.
When finding the largest subarray, record the corresponding start and end positions, that is, the corresponding subscript of the largest subarray.
Time complexity O(n^3)

Divide and conquer

Code block 1

    private int findMaxChildArr(int[] arr, int left, int right) {
        if (left == right) {
            // If the left is equal to the right, it means that there is only one element in this sub array, and it is returned for comparison.
            return arr[left];
        } else {
            // recursive thinking
            int middle = (left + right) / 2;
            // Find the maximum value of the left array;
            int leftMax = findMaxChildArr(arr, left, middle);
            // Find the maximum value of the right array;
            int rightMax = findMaxChildArr(arr, middle + 1, right);
            // Find middle maximum
            int middleMax = findMiddleMax(arr, left, right, middle);
            // Compare the calculated value
            if (leftMax >= rightMax && leftMax >= middleMax) {
                return leftMax;
            } else if (rightMax >= leftMax && rightMax > middleMax) {
                return rightMax;
            } else {
                return middleMax;
            }
        }

    }

Code block 2

    public int findMiddleMax(int[] arr, int left, int right, int middle) {
        int lmidMax = -1000;
        int rmidMax = -1000;
        int sum = 0;
        // Find the maximum prefix to the left
        for (int i = middle; i >= left; i--) {
            sum += arr[i];
            if (sum > lmidMax) {
                lmidMax = sum;
            }
        }
        // Find the maximum suffix to the right
        sum = 0;
        for (int i = middle + 1; i <= right; i++) {
            sum += arr[i];
            if (sum > rmidMax) {
                rmidMax = sum;
            }
        }
        return lmidMax + rmidMax;
    }

1. If the array is divided into two parts, there are only three possible situations for the largest sub array of the array: on the left, on the right, and in the middle (part left, part right)
2. So just compare the maximum L1 on the left, the maximum R1 on the right, and the maximum M1 in the middle. The result is the largest sub array of the whole array.
3. When calculating the left maximum L1 (the right maximum R1), we return to the first point. We can split the array on the left (the right) and find the corresponding left maximum L2 (the right maximum R2), recursively and finally left=right.
4. The maximum value across the middle is another way to find the maximum value from middle - > left and middle - > right respectively, which is the maximum value when connected. See code block 2 for details.
   The time complexity of the algorithm is O(N*LogN), personal understanding: (dichotomy complexity LogN) * (middle to find the maximum N)
   This method did not think how to solve the subscript of the corresponding maximum subarray, under the guidance of children's shoes.

Greedy Algorithm

    @Override
    public void execute() {
        /**
         * sumStart ，sumEnd Represents the start and end bits of the accumulation array respectively
         * It is also equivalent to that sumStart is the previous calculation result and sumEnd is the later calculation result.
         * The potential relationship in the code here is
         * sumEnd = sumStart + arr[end]
         */
        int sumStart = 0;
        int sumEnd = 0;
        int minStart = 0;// Represents the minimum minStart
        for (int endIndex = 0; endIndex < arr.length; endIndex++) {
             // Equivalent to the process of building sumEnd, sumEnd[0..end] = sumEnd[0..end-1] + arr[end]
            sumEnd = sumEnd + arr[endIndex];
            // Find minStart, minStart[j] = min(minStart[j-1],sum[0..j])
            if (sumStart < minStart) {
                minStart = sumStart;
                /**
                 * If sum[0..(endIndex - 1)] (sumstart) < minstart
                 * The start of the largest subarray can only start from endIndex
                 * Generally speaking, the previous endIndex (0~endIndex-1) has been assigned to minStart.
                 */
                this.start = endIndex;
            }
            // Update sumTotal
            if (sumEnd - minStart > maxSum) {
                maxSum = sumEnd - minStart;
                /**
                 * If the maxSum value changes, the end value of the largest subarray is the current endIndex
                 */
                this.end = endIndex;
            }
            sumStart = sumStart + arr[endIndex];
        }
    }

1. Because it is a continuous sub array, there must be end and start for an array to satisfy the formula in the picture
2. So it evolved to solve two of minStart and maxSum, that is, the purpose of two judgments in the code block.

The algorithm is also the best solution known at present. The core idea is that it will use the results of the last cycle, and it does not need to be repeated every time. The comments in the code are detailed and can be realized carefully.
It only traverses the whole array once, with time complexity O(N).

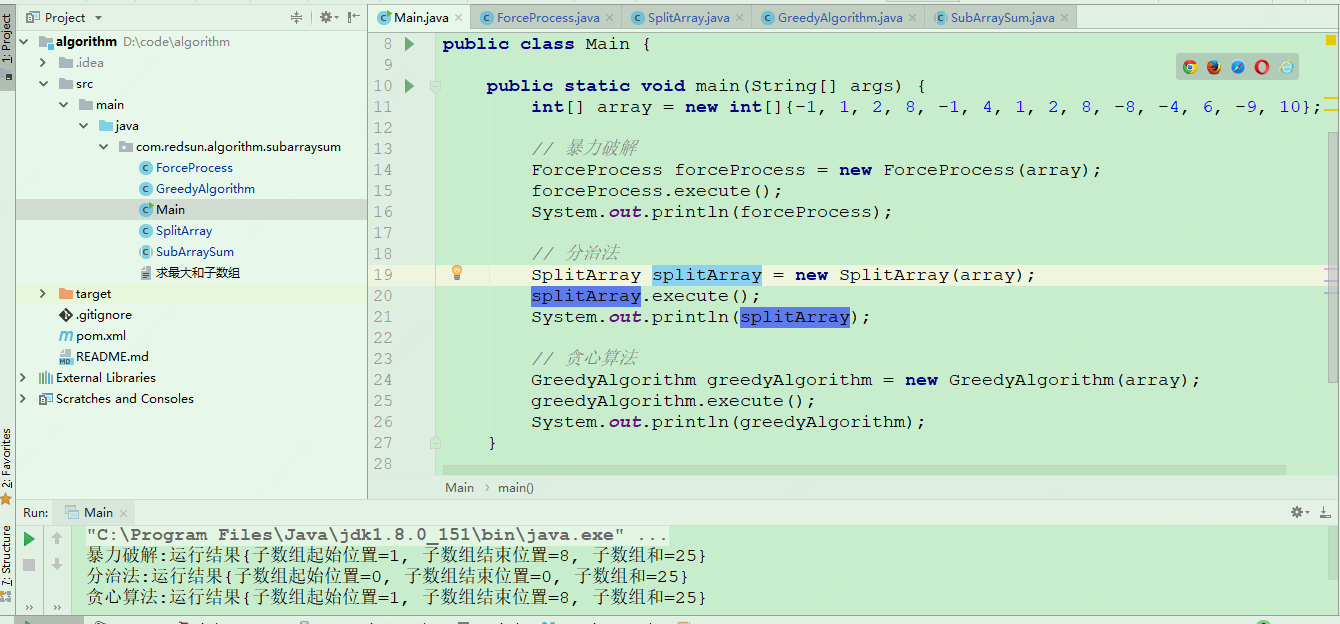
Operation result

The final results of the operation are as follows